加温加压下CFD-PBM 耦合模型空气-水两相流数值模拟研究

2021-10-04张文龙侯燕靳海波马磊何广湘杨索和郭晓燕张荣月

化工学报 2021年9期

张文龙，侯燕，靳海波，马磊，何广湘，杨索和，郭晓燕，张荣月

（1 北京石油化工学院化学工程学院，北京 102617；2 燃料清洁化及高效催化减排技术北京市重点实验室，北京 102617）

引言

鼓泡塔反应器因操作方便、结构简单、传质和传热性好等优点，被广泛地应用在化学、石油化工、生化、制药和冶金等行业[1-3]。鼓泡塔中典型的反应有费-托合成、甲醇的合成以及PX 氧化反应，这些反应需要在高温高压的反应器中进行。由于鼓泡塔中的气液两相流非常复杂，尤其是在高温和高压条件下，需要进行实验或数值模拟以获得一些重要参数，如气含率、气泡大小分布、液体速度分布和气泡上升速度等，以分析塔中的流体动力学行为与传质特性。在这些参数中，气含率是影响鼓泡塔中流体行为的最重要参数之一，大多数气含率是常温和常压下的实验数据。而在工业生产中，鼓泡塔中的反应通常在升温加压的条件下完成。因此，了解近实际工况下鼓泡塔流体力学特性将更有意义。

近几十年来，国内外开展了广泛的气-液鼓泡塔内的实验和模拟研究，现有文献研究较多的是压力变化对气含率的影响，而升温对气液两相鼓泡塔影响在文献中较为少见，主要研究物性变化的影响规律[4]。Deckwer 等[5]以Fischer-Tropsch 过程为背景，在直径为4.1 cm 和10 cm 的浆液鼓泡塔反应器中研究了温度和压力变化对气含率和传热传质的影响。Behkish 等[6]对N2、He/异构烷烃体系研究发现，在温度30～200℃范围内，总气含率随温度的升高而增加，加入固相后，增加的固体浓度会使气含率显著降低。Pohorecki 等[7]在0.3 m 鼓泡塔中研究了N2在环己烷中的流体力学行为，发现温度升高导致液体表面张力降低，气含率增加，而平均气泡直径随温度升高而降低。升温更多表现为气液物理性质的变化，而对气泡行为的影响尚未完全揭示，或者缺乏准确统一的解释。因此，研究温度变化对气含率的影响机理具有十分重要的意义。

计算流体力学（CFD）方法已经成为鼓泡塔反应器模拟和优化的重要工具。计算流体力学与群体平衡模型结合（CFD-PBM）可有效地模拟鼓泡塔内流体行为[8]。对于鼓泡塔中的气液两相流动常见的模拟方法有欧拉-欧拉方法和欧拉-拉格朗日方法。欧拉-欧拉模型假设气液两相之间相互渗透，不直接追踪每一个气泡的运动，大大降低了计算量而被广泛应用[9-10]。欧拉-欧拉模型需要相间作用力来进行封闭，而曳力是气-液系统中一种最重要的作用力，其直接影响模拟结果的准确性[11-13]。目前，单气泡曳力模型到气泡群曳力模型的转变较为复杂。Buffo 等[14]发现CD（气泡群曳力系数）等于CD（0单气泡曳力系数）乘以与液含率有关的系数。而在气液鼓泡塔的模拟中，气泡群曳力系数较为常用。Roghair 等[15]在欧拉-拉格朗日模型基础上，采用直接模拟得到气泡群曳力的闭合模型。Wang 等[16]在Tomiyama[17]单气泡曳力模型基础上提出大气泡加速效应，引入大气泡气含率修正气泡群曳力模型。Yang 等[18]基于单气泡尺寸（SBS）模型提出了双气泡尺寸（DBS）模型，DBS 模型可以合理地预测空气-水系统中发生流态转变的气体速度。Yang 等[19]基于双气泡尺寸（DBS）模型导出简化的曳力模型应用于CFD 模拟，DBS 的曳力模型无须调整模型参数即可合理地预测径向含气量分布和两相流场。Qin 等[20]采用了EMMSPBM 的方法对液-液体系的液滴尺径分布进行了修正，提高了原有模型的准确度。Yang 等[21]率先提出了基于EMMS 方法的群平衡（PBM）模型模拟鼓泡塔内流体行为，模拟结果表明了该模型可以合理地模拟低气速鼓泡塔中的气泡粒径分布。本文在较宽表观气速下对浆液鼓泡塔升温加压，对Yang 等[19]的曳力模型进行修正，通过CFD-PBM 耦合模型进行数值模拟，并与实验数据进行对比，以验证该模型的可行性。

1 数学模型

1.1 双流体模型

气液系统模拟采用欧拉-欧拉模型，又称双流体模型（TFM）。该模型相对于欧拉-拉格朗日模型与直接模拟，不仅较好地考察了塔内气含率的分布且大大提高了运算速度。控制方程如下。

质量守恒方程：

动量守恒方恒：

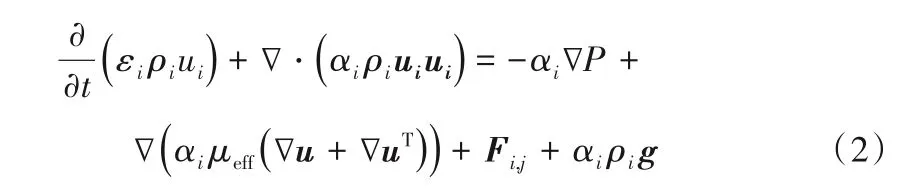
式中，i为气相g 或液相l；α、ρ、u、t分别为相含率、密度、速度矢量和时间；P为压力；μeff为流体有效黏度。

1.2 湍流方程

湍流方程模拟了湍动状态下的气液系统。本文选择雷诺时均法（RANS）中的标准k-ε模型[22]，该模型的优点在于适用性广，计算量较小。方程具体描述如下。

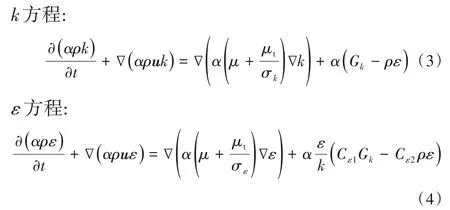
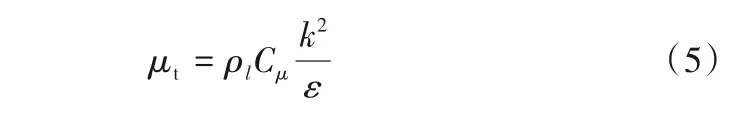
式中，Cε1=1.44,Cε2=1.92,σk=1.0,σɛ=1.3。

1.3 相间作用力模型

欧拉-欧拉模型需要相间作用力来封闭，相间作用力的选择对于模拟结果的精度十分重要。本文模拟选择了曳力、升力、壁面润滑力和湍流扩散力，忽略了虚拟质量力的作用。具体表达式如下：

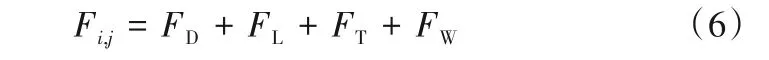
1.3.1 曳力曳力是一种最主要的相间作用力。本文以Yang 等[19]在常温常压空气-水体系中的双尺度最小能量化曳力模型为基础，在加压加温的空气-水体系中，考虑压力因素的影响，引入密度参数对公式进行了修正；考虑温度因素的影响，引入黏度和表面张力等参数对公式进行了修正。修正后的公式适用于加温加压的空气-水体系的数值模拟。具体表达式如下：

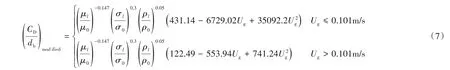
1.3.2 升力升力是气泡上升方向垂直的一种作用力。径向升力对于气含率的径向分布至关重要，本文采用的升力表达式如下[23]：

1.3.3 壁面润滑力壁面润滑力是由靠近壁面处气液速度梯度引起的，是使气泡远离鼓泡塔壁面的一种力，本文采用Frank 等[24]的壁面润滑力，具体表达式如下：

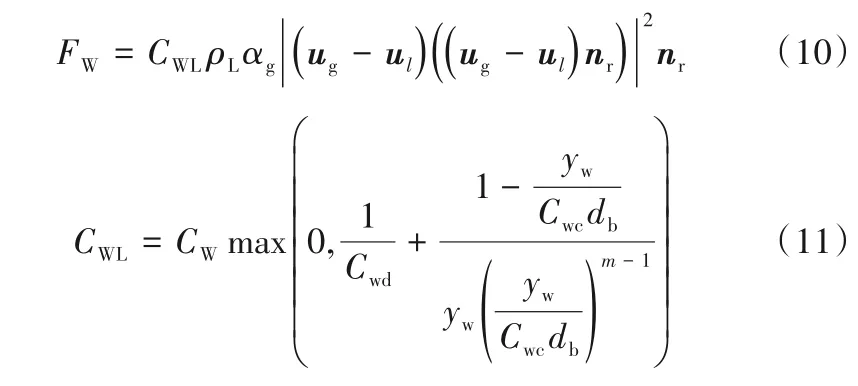
式中，nr为壁面外法向向量；Cwd、Cwc为无量纲常数；m=1.5～2；CW为壁面润滑力系数，CW是关于Eo的函数，具体表达式如下：

1.3.4 湍流扩散力湍流扩散力是由液相湍流旋涡引起的，此力使得径向气含率分布更均匀。本文采用Lopez de Bertodano[25]的湍流扩散力，具体表达式如下：

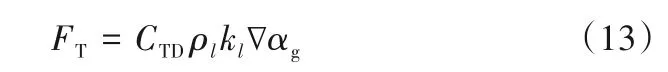
式中，kl为湍流强度；CTD为湍流扩散力系数，其取值范围是0.1～1，本文中取值为1。

1.4 群体平衡模型

群体平衡模型（population balance model，PBM）是描述反应器中颗粒或气泡大小分布的一种方法。反应器中颗粒或气泡大小分布对体系的混合、传质传热及反应都有影响。而在鼓泡塔中，气泡主要发生破碎和聚并，因此该状况下群体平衡模型表示如式(14)：

式中，V为母气泡体积；V'为子气泡体积；n(V',t)为体积为V'的气泡数密度函数；c(V-V',V')为气泡聚并速率；β（V,V'）为体积V的气泡破裂成体积V'的子气泡分布函数。

1.4.1 破碎模型气泡破碎模型主要是由气泡破碎速率和子气泡大小分布构成，而引起气泡破碎的机理主要分为由湍流旋涡与气泡碰撞引起的破碎、大气泡由于表面不稳定性引起的破碎。目前应用广泛的气泡模型主要以Luo 等[26]和Lehr 等[27]破碎模型为主。本文采用Luo 等的气泡破碎模型，具体公式如下：

1.4.2 聚并模型气泡聚并速率可表示为：

气泡间碰撞频率为：

基于Luo 等[28]的聚并效率模型，将改进的聚并系数Ce引入气泡聚并效率模型中。修改后的聚并模型为：

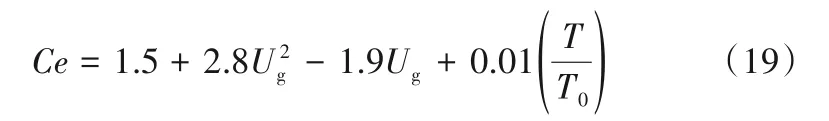
2 加压加温实验

如图1 所示，鼓泡塔实验装置高为1.3 m，内径为0.1 m，塔底分布器开孔率为1.78%。气体从压缩机流出，至压力储罐，经转子流量计、调节阀、分布板进入加压鼓泡塔，从塔顶流出，经冷凝器、气液分离器、吸收塔，由截止阀至压力储罐，再进入压缩机，完成一个循环。在鼓泡塔高为0.2、0.3 和0.4 m测量点放置了3个用于测量压差的压力传感器。

图1 实验装置流程图Fig.1 Experimental device

3 模型求解方法

本文以FLUENT 15 作为计算平台，采用非稳态分离求解器求解模型方程。设置速度为入口边界条件，压力为出口边界条件。PBM 模型采用离散方法求解，气泡大小按照等体积比方法离散为16组子气泡。模拟的时间步长固定为0.002 s，并认为在60 s内达到了准稳态。当鼓泡塔内的模拟达到稳定后，获取了塔高为0.3 m 处截面的时间平均径向气含率和气泡直径分布等数据。该模拟的对象是空气-水体系，温度T变化范围为30～160℃，模拟的压力为1 MPa，表观气速的范围为0.08～0.24 m/s，塔中静态高度H0为0.5 m。

3.1 模拟的气液物性

表1 为气液两相的物性，固相为TA（terephthalic acid），TA 的平均粒径为0.12 mm，密度为1510 kg/m3。从表中可以看出，随着温度的升高，液相水黏度降低，表面张力降低。随着固体浓度增大，浆态水的密度增大，黏度增大，表面张力基本不变。

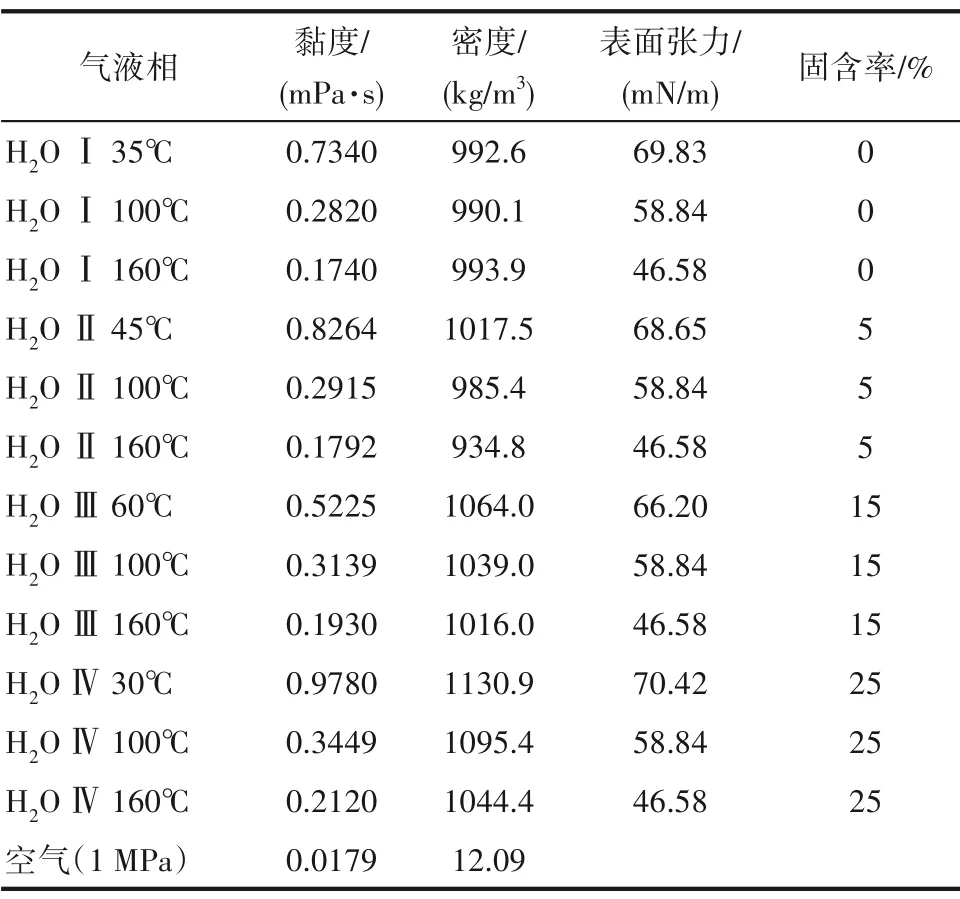
表1 气液物性Table 1 Physical properties of gas and liquid

3.2 网格无关性验证

图2 为三种二维非结构性网格的划分，其中Grid 1、Grid 2 和Gird 3 三种网格的网格数分别为900、1690 和4160 个。图3 为35℃下0.08、0.12、0.18和0.24 m/s 四种不同表观气速下三种不同质量网格的平均气含率对比。从图中可以发现，Grid 1 平均气含率模拟结果略低于Grid 2 和Gird 3 的模拟结果，而Grid 2 和Gird 3 模拟结果基本接近相同。同时，当网格数量达到一定值后，网格数的增加只会增加计算量，而计算精度没有提高，因此综合考虑计算时间和精度的情况下，选择了Grid 2 中尺寸二维的网格进行模拟。

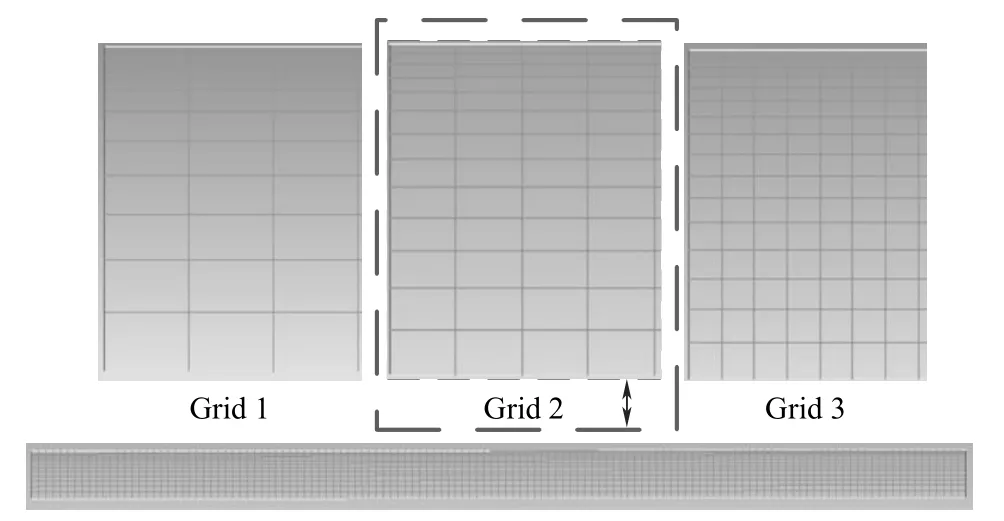
图2 不同质量网格的划分Fig.2 Partition of different quality grids

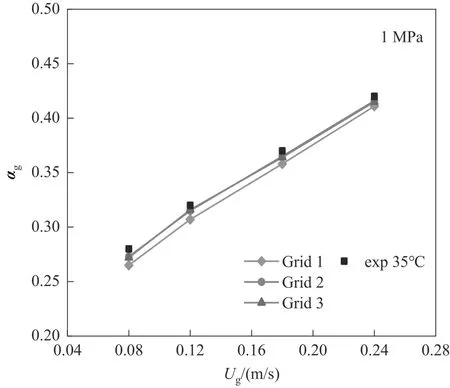
图3 不同网格质量对平均气含率的影响Fig.3 The influence of different mesh quality on average gas holdup

4 结果与讨论

4.1 表观气速对平均气含率的影响

图4 为不同温度下空气-水体系表观气速与平均气含率的关系。表观气速Ug是鼓泡塔中最重要的操作参数之一，决定着流动状态和相结构组成。因为实验与模拟的气速范围均处于湍流区，在相同温度下，平均气含率随着表观气速的增大而单调增加。通过模拟发现，在35、100 和160℃下的模拟结果和实验值基本吻合，且误差较小。因此，修正的CFD-PBM 模型在不同温度和较宽的表观气速下可较好地预测相关的流体力学参数。

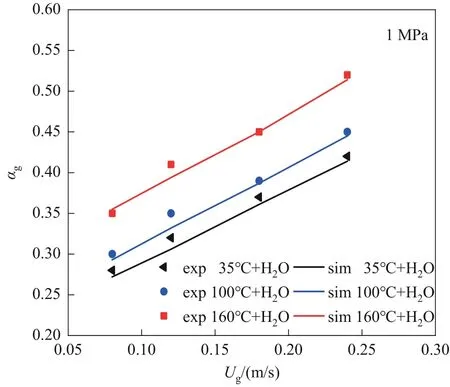
图4 不同温度下空气-水体系表观气速与平均气含率的关系Fig.4 The relationship between superficial gas velocity of airwater system and average gas holdup under different temperatures

4.2 温度对平均气含率的影响

图5 为不同温度下空气-水体系温度与平均气含率的关系。从图中可以看出，在相同表观气速下，平均气含率随温度的升高而增加，而且温度越高，平均气含率增加的幅度也越大。温度对气含率的影响要同时考虑液体物理性质的变化和蒸汽压的变化这两个因素[29]。塔内温度较低时，平均气含率的变化主要受前者的影响；塔内温度接近水的沸点或者超过水的沸点时，两种因素都产生影响，但以后者为主。当塔内温度从35℃升到100℃时，液相水的黏度和表面张力降低，从35℃升到100℃和从100℃升到160℃，水的表面张力和黏度分别下降了16%和62%，在这两种物理性质中，表面张力的变化对气含率的影响较大，因为当表面张力降低时，维持气泡形状的内聚力减小，这导致大气泡产生不稳定性，使大气泡破碎成小气泡，塔内的平均气含率增加。平均气含率在低黏度范围内随着黏度的减小而减小，而黏度的变化对气含率的影响较小。因此，平均气含率在此温度范围内增加。

图5 不同温度下空气-水体系温度与平均气含率的关系Fig.5 The relationship between temperature of air-water system and average gas holdup under different temperatures

当塔内温度升高到100℃和160℃时，水的表面张力和黏度分别下降了21%和76%，水的物理性质的变化使得塔内气含率增加。另外，当温度超过水的沸点时，塔内液相蒸发，气相所占比例增大，塔内蒸汽压增大，也导致平均气含率增加。这也是在较高温度下比较低温度下气含率增加幅度较大的原因。从图中还可以看出，模型模拟结果和实验测量值基本吻合，因实验仅为平均气含率数据，下文将采用模拟结果来解释温度的变化对流体动力学变化规律的影响。

4.3 固含率对平均气含率的影响

图6为不同固含率下空气-水TA 体系平均气含率分布。从图中可以看出，平均气含率随着表观气速的增加而增加，且表观气速越大，平均气含率增加趋势越小。因为气含率的变化趋势取决于鼓泡塔中流型的变化。在非均匀流动状态下，由于大气泡的尾流加速效应，塔中气泡受到的阻力降低，平均气含率增加趋势减小。塔中温度升高，平均气含率明显增加。而且温度差别越大，平均气含率增加幅度也越大，在固含率为15%的条件下，温度从100℃到160℃的气含率增加量明显高于温度从60℃到100℃的气含率增加量，因为温度升高，塔内液相水蒸发，塔内蒸汽量增大。因此，塔内温度越高，平均气含率增加的幅度越大。在误差10%范围内，模型的模拟结果和实验值基本吻合。

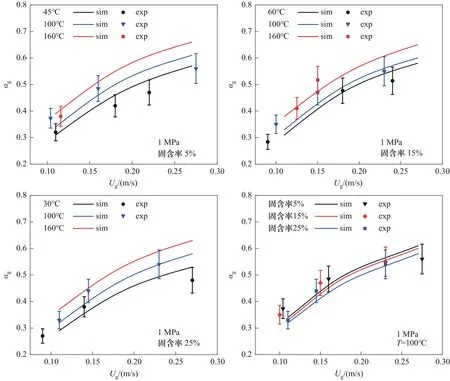
图6 不同固含率下空气-水TA体系平均气含率分布Fig.6 The distribution of average gas holdup of air-water TA system under different solid holdups

在100℃的5%、15%和25%三种不同固含率下，随着固体浓度的增加，平均气含率减小，但固含率从5%增加到15%，以及从15%增加25%，平均气含率变化幅度不大。固体颗粒对气含率的影响不仅考虑固体浓度，还应考虑颗粒的性质、大小和密度，这些均可能会影响气含率[30]。随着塔内固体浓度的增加，浆态水的黏度增加，黏度的增加使得塔内气泡的聚并增加，塔内的小气泡减少，气含率减小。但固含率从5%到25%的变化范围内，黏度的变化幅度很小，因此平均气含率也只是略微减小。实验值和模拟结果在10% 的误差范围内基本吻合。

4.4 空气-水体系大小气泡气含率

图7 为35、100 和160℃三种不同温度下，表观气速对总气含率、大气泡气含率和小气泡气含率的影响。在本文的模拟中，使用Ishii 等[31]的相关式来区分小气泡和大气泡，即dc=4[σ/g(ρl-ρg)]。从图中可以看出，随着表观气速的增大，总气含率、大气泡气含率及小气泡气含率都有相应程度增加。但随着表观气速的增大，大气泡气含率增加的幅度大于小气泡的，这也与Zhang 等[8]的研究结果一致。产生这种结果的原因是随着塔内表观气速的增大，增加了塔内气泡的聚并，大气泡数量增多，这使得大气泡的气含率增加幅度较大。

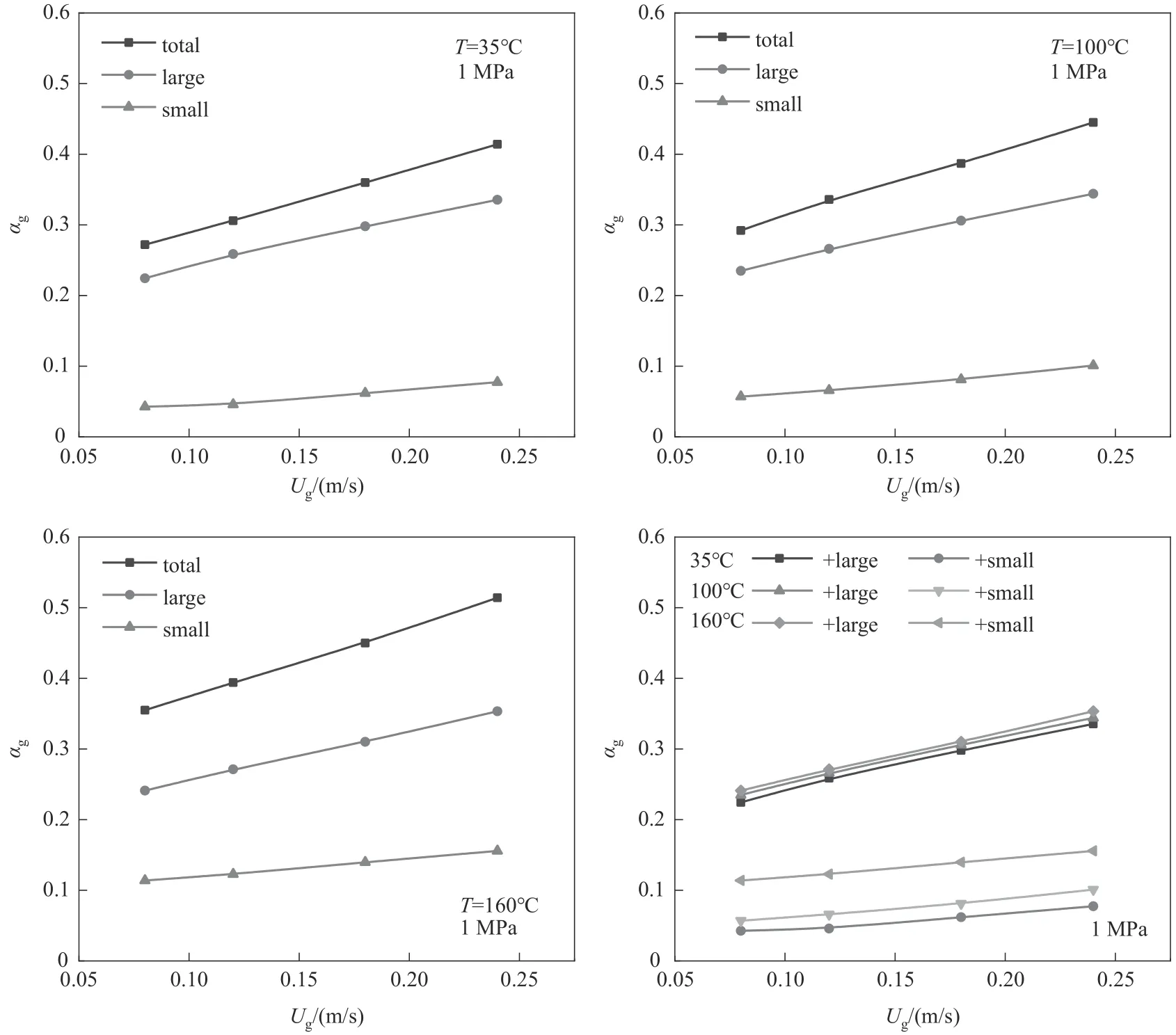
图7 不同温度下空气-水体系温度与大小气泡气含率的关系Fig.7 The relationship between temperature of the air-water system and large and small bubbles gas holdup under different temperatures

在相同表观气速下，随着塔内温度的升高，总气含率明显增加，这是因为随着温度的升高，液相水的表面张力和黏度减小，这两种液体性质中表面张力影响尤为突出，表面张力减小使得气泡的稳定性变弱，这导致大气泡破碎成小气泡，使得塔内的总气含率增加。塔内小气泡数密度的增加，使得小气泡的气含率较大程度增加，大气泡气含率略微增加。

4.5 空气-水TA体系大小气泡气含率

图8 为100℃下不同固含率空气-水TA 体系大小气泡气含率的关系。从图中可以看出，随着固含率的增加，总气含率减小，大气泡气含率略微增加，小气泡气含率减小。这是因为随着TA 固体含量的增加，增加了塔内气泡聚并行为的发生，并且抑制了塔内气泡的破碎，塔内小气泡的数量减少，使得塔内小气泡气含率减小。随着TA 固体含量的增加，塔内总气含率减小，因此大气泡气含率增加的幅度小于小气泡气含率减小的幅度。

图8 不同固含率下空气-水TA体系大小气泡气含率的关系Fig.8 The relationship of large-bubble and small-bubble gas holdup of air-water TA system with different solid holdups

4.6 空气-水体系径向气含率分布

图9 为不同温度下空气-水体系的径向气含率分布。从图中可以看出，径向气含率从塔中心到塔壁处逐渐减小。在相同温度下，径向气含率随表观气速的增大而增加；相同表观气速下，径向气含率随温度的升高而增加，这与平均气含率随温度升高的变化规律一致。并且随着温度的升高，径向气含率变化趋势越来越平缓。Chabot 等[32]研究表明温度升高改善了气泡径向分布的均匀性，导致径向气含率变化趋势更加均匀，增大了塔内的气含率。

图9 不同温度下空气-水体系的径向气含率分布Fig.9 Radial gas holdup distribution diagram of air-water system at different temperatures

4.7 空气-水体系轴向截面气含率云图分布

图10为不同温度和表观气速下空气-水体系轴向对称截面气含率云图分布。图10（a）为35℃下，不同表观气速的气含率云图分布；图10（b）为0.12 m/s 的表观气速下，不同温度的气含率云图分布。不同云图左侧边为塔的中心对称轴，右侧边为塔的壁面。从图中可以看出，气含率在塔中心较大，壁面处较小，而且气含率随表观气速和温度的升高而增加，其变化规律和径向气含率变化规律相同。但是从轴向气含率云图分布可以看出气含率的变化趋势。随着温度和表观气速的增加，塔中的液面也随之升高，且在鼓泡塔中充分发展区域，气含率的大小分布基本一致。李兆奇[33]通过对列管型鼓泡塔中流动发展规律的研究认为，在鼓泡塔充分发展阶段，气含率不会受到塔高变化的影响。这与本部分的研究结果相同。

图10 空气-水体系轴向截面气含率云图分布Fig.10 Distribution diagram of air holdup contours in axial section of air-water system

4.8 空气-水体系轴向液速分布

图11 为不同温度和表观气速下轴向液速分布。从图中可以看出，轴向液速从塔中心到塔壁处逐渐减小，在r/R约为0.7 的近塔壁处轴向液速呈现向下的趋势（出现了负值）。在相同的温度下，轴向液速随表观气速的增大而增大，这是因为轴向向上的气速对塔内液体施加了向上的作用力，且表观气速越大，所施加的作用力越大，轴向液速越大；在相同表观气速下，随着塔内温度的升高，轴向液速基本没变化，这是因为随着温度的升高，只改变了液体的表面张力和黏度等物理性质。只有物理性质发生变化，并不会引起塔内轴向液速的变化。

图11 不同温度下空气-水体系轴向液速分布Fig.11 Radial distribution of liquid velocity at different temperatures

4.9 空气-水体系气泡直径分布

图12 为不同温度下空气-水体系气泡直径分布。从图中可以看出，在相同温度下，随着表观气速的增加，气泡直径增大。这是因为随着表观气速增加，塔内气泡聚并的概率增大，小气泡聚并形成大气泡，进而导致塔内大气泡变多，使得塔内气泡尺寸变大。在相同表观气速下，随着塔内温度的升高，气泡直径呈现出减小的趋势。这是因为随着塔内温度升高，水的表面张力减小，这使得维持气泡形状的内聚力减小，大气泡稳定性减弱，使大气泡破碎成小气泡；同时温度超过水的沸点时，液相水大量蒸发成蒸汽，体系内蒸汽压增大，也有利于大气泡破碎形成小气泡，使得塔内气泡直径有减小的趋势。

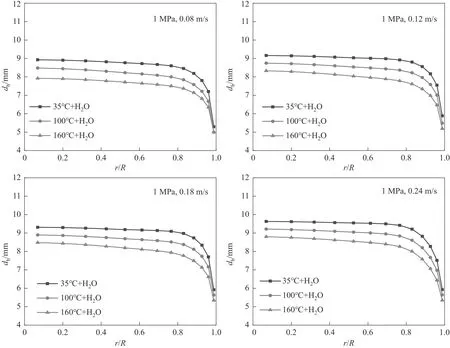
图12 不同温度下空气-水体系气泡直径分布Fig.12 The bubble diameter distribution diagram of air-water system at different temperatures

4.10 空气-水体系气泡数密度分布

图13为不同温度下空气-水体系温度与气泡数密度分布的关系。从图中可以看出，气泡尺寸为7～8 mm 的气泡数量最多。在相同温度下，随着表观气速的增加，大气泡数量相对增多，小气泡数量相对减少，子气泡分布范围变宽。这是因为随着表观气速的增加，塔内气泡聚并的概率增大，使得小气泡聚并成大气泡，气泡分布范围变宽。在相同表观气速下，随着温度的升高，塔内液相的表面张力减小，蒸汽压增大。液相表面张力的减小使得维持气泡形状的内聚力减小，有利于塔内大气泡破碎成小气泡；蒸汽压的增大，使得气泡携带的能量增加，增大了气泡与气泡和气泡与湍流旋涡的碰撞概率，小气泡数量增多，小气泡分布范围变窄。

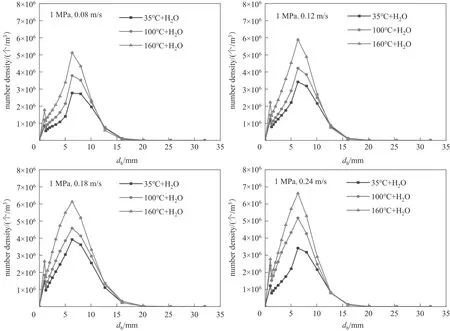
图13 不同温度下空气-水体系温度与气泡数密度分布的关系Fig.13 The relationship between temperature of air-water system and bubble number density distribution under different temperatures

5 结论

本文通过对加压加温鼓泡塔中空气-水体系气-液两相流的CFD-PBM耦合数值模拟，研究了温度对鼓泡塔中流体力学行为的影响，具体结论如下。

（1）在加温加压鼓泡塔内，通过对35、100 和160℃三个温度下的数值模拟，结果表明，表观气速增大，平均气含率增加；固含率增加，平均气含率减小；温度升高，平均气含率增加，且平均气含率在温度越高的情况下增加幅度越大。这是因为温度升高，液相水表面张力的减小和塔内蒸汽压的增大导致大气泡破碎成小气泡，平均气含率增加。而且通过模拟发现,平均气含率的模拟结果和实验值在10%的误差范围内吻合较好。

（2）塔内表观气速增大，空气-水体系的总气含率、大气泡气含率及小气泡气含率都有相应程度的增加，但大气泡气含率增加的幅度大于小气泡的。固含率增加，总气含率减小，小气泡气含率减小；温度升高，总气含率明显增加，小气泡的气含率有较大程度增加，大气泡气含率略微增加。这是因为温度升高，液相水表面张力的减小和塔内蒸汽压的增大导致大气泡破碎成小气泡。因此，总气含率和小气泡气含率都增加。

（3）塔内表观气速增大，气泡尺寸变大；温度升高，气泡尺寸变小。在相同温度下，表观气速增加，气泡聚并行为增强，大气泡数量相对增加，子气泡分布范围变宽；但在相同表观气速下，温度的升高，液相水表面张力的减小和塔内蒸汽压的增大导致大气泡破碎成小气泡，气泡数密度增加，子气泡分布范围相对变窄。

符号说明

b（fv,d）——尺寸为d的气泡破碎速率

CD——曳力系数

CL——升力系数

CTD——湍流扩散力系数

Ce——聚并系数

D——鼓泡塔内径，m

db——气泡直径，mm

Eo——Eötvös数

fv——破碎速率

H——鼓泡塔高度，m