永磁电机不平衡磁拉力及脉动转矩相位调谐分析

王世宇 ，霍咪娜，修 杰，宋轶民，刘建平，曹树谦

(1. 天津大学机械工程学院，天津 300072；2. 天津市非线性动力学与混沌控制重点实验室，天津 300072；3. 天津大学电气与自动化工程学院，天津 300072)

永磁电机是一种以磁场为媒介的机电能量转换装置，具有节能、环保、结构简单等显著优点．最具代表性的永磁电机是稀土钕铁硼(NdFeB)电机，其具有高效节能、运行可靠且不含战略金属钴等显著优点．然而，该类电机本质上为含脉动激励的对称系统，因而将不可避免地产生磁致振动．在许多重要应用领域，振动水平是衡量电机性能的关键技术指标．

现有文献对永磁电机的振动抑制问题开展了广泛而深入的研究，已提出许多卓有成效的方法，例如槽极组合[1-16]、斜槽[11]、斜极[11]、辅助槽[17]、极弧系数调整[18]及磁极偏移[19]等．应当指出，为了降低成本，需要在设计阶段开展振动预测及抑制工作．槽极组合是一种可在设计阶段实施的最简便、最经济的减振手段，同时也是其他减振方法顺利实施的基本前提．现有文献对槽极组合问题开展了许多研究．文献[1]验证了整数槽电机的减振效果．文献[2]指出：增大槽极组合的最小公倍数可有效抑制转矩脉动．文献[7]认为增大槽极组合的最小公倍数且减小其最大公因子可有效抑制转矩脉动．文献[13]认为槽极数互质有利于减小转矩脉动．显然，上述结论具有一致性，即增大最小公倍数可以抑制振动．然而，对于槽极公因子的相关分析，现有文献还存在分歧．文献[11]认为当槽极最大公因子大于 1时，可抑制不平衡磁拉力．文献[12]认为偶数槽可抑制不平衡磁拉力．但文献[13]认为若槽极最大公因子为 2，4，6，…，或 3，9，15，…，可抑制不平衡磁拉力；若为 1，5，7，…，则会激起不平衡磁拉力．由于磁极数均为偶数，因而文献[11-12]所得结论相同．尽管文献[13]研究了最大公因子与不平衡磁拉力的关系，但所得结论与文献[11-12]相矛盾．

综上分析，笔者将研究永磁电机的槽极组合与不平衡磁拉力及脉动转矩的关系，澄清现有文献之间的分歧．鉴于该类电机的机械及电磁对称性以及内在激励的脉动性，在具体研究过程中，将借鉴行星传动领域的相位调谐方法(Planet phasing)[19-20]研究永磁电机的磁拉力特性．

1 数学建模

1.1 基本假设

为方便分析，现作如下假设：①将磁拉力等效为作用于定子齿几何形心的等效集中力；②定/转子均为刚体且有3个自由度：2平移，1转动；③满足机械及电磁对称条件；④定子处于开路状态．

1.2 数学模型

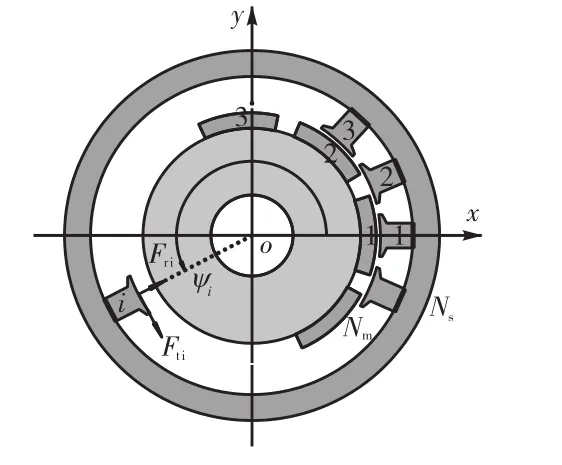
图1 磁拉力示意Fig.1 Schematic of magnetic pull

图 1为内转子永磁电机的计算模型．图中 Ns和Nm分别为齿槽数和磁极数，坐标系 xoy固接于定子．不失一般性，假定x轴指向第 1个定子齿的几何形心，则该定子齿与x轴正向的夹角ψ1=0，因此第i(i = 1 , 2,⋅⋅⋅, Ns)个定子齿的相应夹角ψi= 2 π(i − 1 )/Ns.图中 Fti和 Fri分别为作用于第i个定子齿的切向及径向磁拉力．

1.3 磁拉力相位分析

在永磁电机中，主磁通沿径向进入气隙，进而产生作用于定子的径向及切向磁拉力．在坐标系 xoy下，转子每旋转 1周，所有磁极将与某一特定的定子齿扫过mN 次，相应的磁拉力脉动频率

式中0ω为电机的转速．

第i个定子齿与x轴的夹角

作用于相邻定子齿的磁拉力相位差

由式(2)和式(3)可得作用于第i个定子齿的磁拉力相角

式(4)描述了磁拉力之间的相位超前及滞后关系．

1.4 不平衡磁拉力分析

假定作用于第 i个定子齿的径向及切向磁拉力分别为

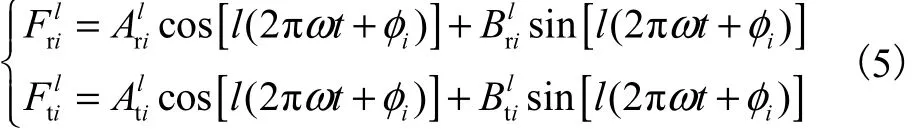
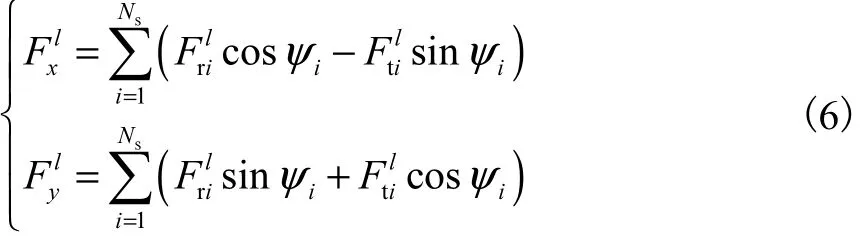
对整数m和N，有[20]

为方便分析，定义相位调谐因子

式中 m od ( a /b)表示a除以b的余数．根据三角函数的运算特性，式(6)右端各项取值规律相似．篇幅所限，仅分析第1项，即

1.5 脉动转矩分析

仍然采用傅里叶级数分析由切向磁拉力形成的转矩脉动规律．假定作用于第i个定子齿的力矩为

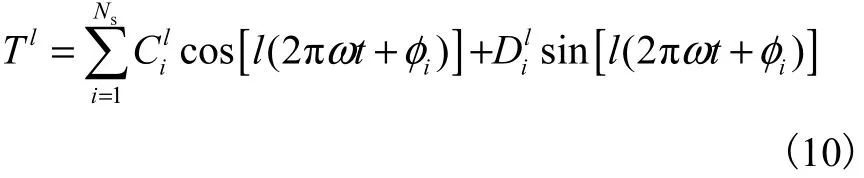
1.6 相位调谐映射关系

改变槽极组合将引起齿槽与磁极相对位置的改变，进而影响电机的受力及振动特性．由上述结果可得：①若 k = 0 ，将抑制不平衡磁拉力，同时激起脉动转矩；②若 k =1 或 Ns−1，将产生不平衡磁拉力，同时抑制脉动转矩；③若 k =2, 3, 4, … , Ns−2，将同时抑制不平衡磁拉力和脉动转矩．图 2以四齿定子为例示出了 3种典型的受力状态．相应地，定子将分别呈现扭转振动模式(rotational mode，RM)、平移振动模式(translational mode，TM)和平衡模式(balanced mode，BM)．进一步分析可知，若槽极最大公因子为Q，则相位调谐因子的取值满足 k ∈ [ Q ,− Q ][16,21]，据此可得表 1所述规律．此外，若 Q ＞1，将抑制不平衡磁拉力．该结论与文献[11-12]相符．但是，应当指出的是，随着磁拉力谐波阶次的变化，定子可呈现扭转振动或受力平衡状态．

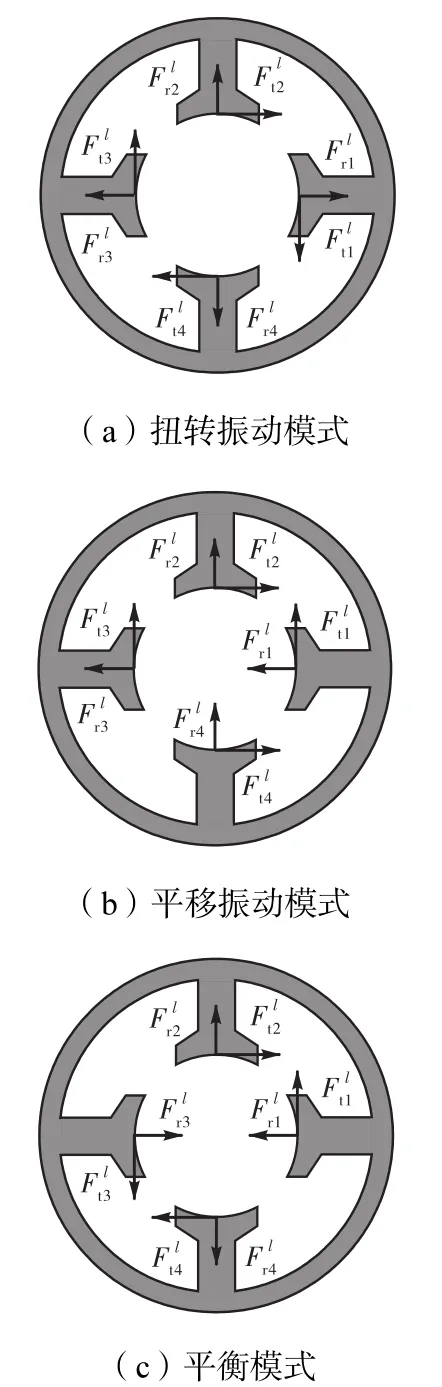
图2 定子受力示意Fig.2 Magnetic forces on stators

表1 永磁电机相位调谐Tab.1 Phase tuning of PM motors

2 仿真验证

2.1 仿真算例及磁拉力计算方法

为验证相位调谐规律的正确性，设计了激励相位不同的永磁电机，仅调整了齿槽数，使电机的差别主要体现在槽极组合及其产生的受力特性．具体配合为8极15槽和8极12槽，其他参数见表2．

表2 永磁电机基本参数Tab.2 Basic parameters of PM motors

为验证磁拉力的叠加效果，在仿真过程中，分别计算作用于单个定子齿的切向及径向磁拉力，然后分析其叠加效果．为了清晰地显示磁拉力的变化规律，还采用瞬态磁场有限元及麦克斯韦应力张量法计算每个瞬时的径向及切向磁拉力．磁拉力的离散计算格式为

式中0μ、N、rB、tB、r和θΔ分别为真空磁导率、路径的离散点个数、径向磁通密度、切向磁通密度、半径和旋转步长．

2.2 8极15槽电机

图3为某一瞬时8极1槽和8极15槽电机的磁力线分布．图 4为该瞬时的径向及切向气隙磁通密度．磁极和齿槽数越多，磁力线分布越均匀，因而 8极15槽电机的磁力线分布更加对称．

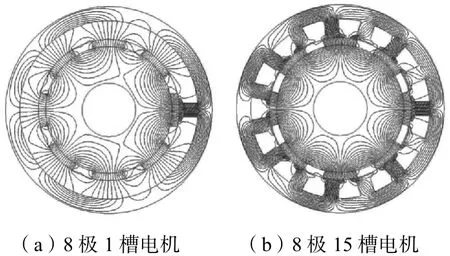
图3 磁场分布Fig.3 Flux distribution

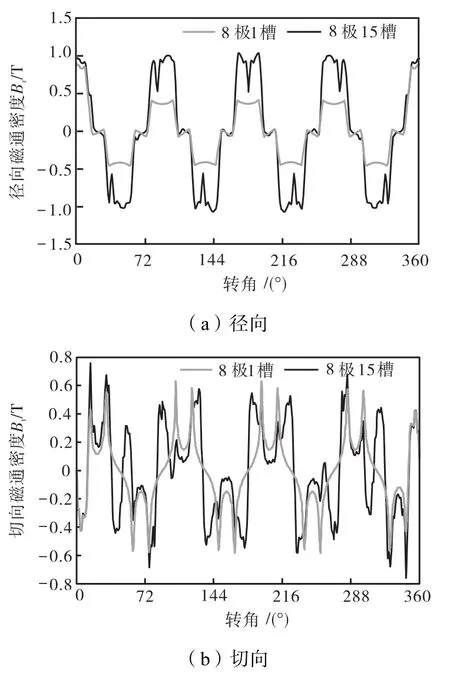
图4 气隙磁通密度(8极15槽)Fig.4 Air-gap magnetic flux density(8,pole/15,slot)

图5 永磁电机不平衡磁拉力(8极15槽)Fig.5 UMP of PM motors(8,pole/15,slot)

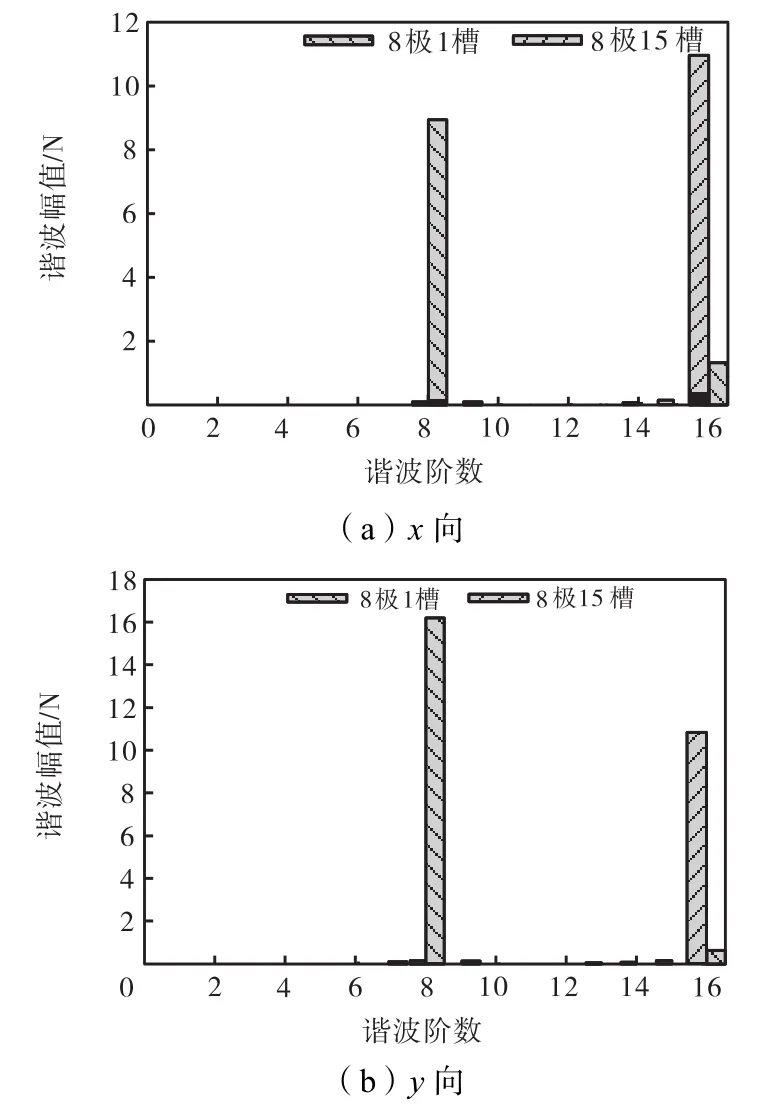
图6 不平衡磁拉力谐波分析(8极15槽)Fig.6 Fourier analysis of UMP(8,pole/15,slot)

图 5为不平衡磁拉力的仿真结果．若忽略计算误差，两个正交方向的磁拉力变化规律基本相同，仅初始相位不同．对其进行谐波分析，可得图 6所示结果．由图6可知，8极1槽电机的磁拉力存在第8阶和第 16阶谐波．转子旋转 1周，作用于定子齿的磁拉力将脉动8个周期，因此第8阶和第16阶谐波应分别为等效基波和等效2阶谐波．显然，8极15槽电机抑制了等效基波，存在等效 2阶谐波．由表 1可知，与等效第1阶和第2阶谐波对应的相位调谐因子分别为8和1，此时分别抑制和激起不平衡磁拉力．上述仿真结果与本文的理论分析相符．

图 7为脉动转矩及其谐波分析．与径向磁拉力的分析过程相同，转子仍然旋转 1周，转矩也脉动了8个周期，所以第8阶谐波即为等效基波．从图7(b)可以看出，8极1槽电机转矩的等效基波和等效2阶谐波较显著，而这两阶谐波在 8极 15槽电机中均受到不同程度的抑制．由表 1可知，若等效谐波阶数为1和 2，则相位调谐因子分别为8和1，此时恰好抑制转矩脉动．上述仿真结果与本文的理论推导一致．

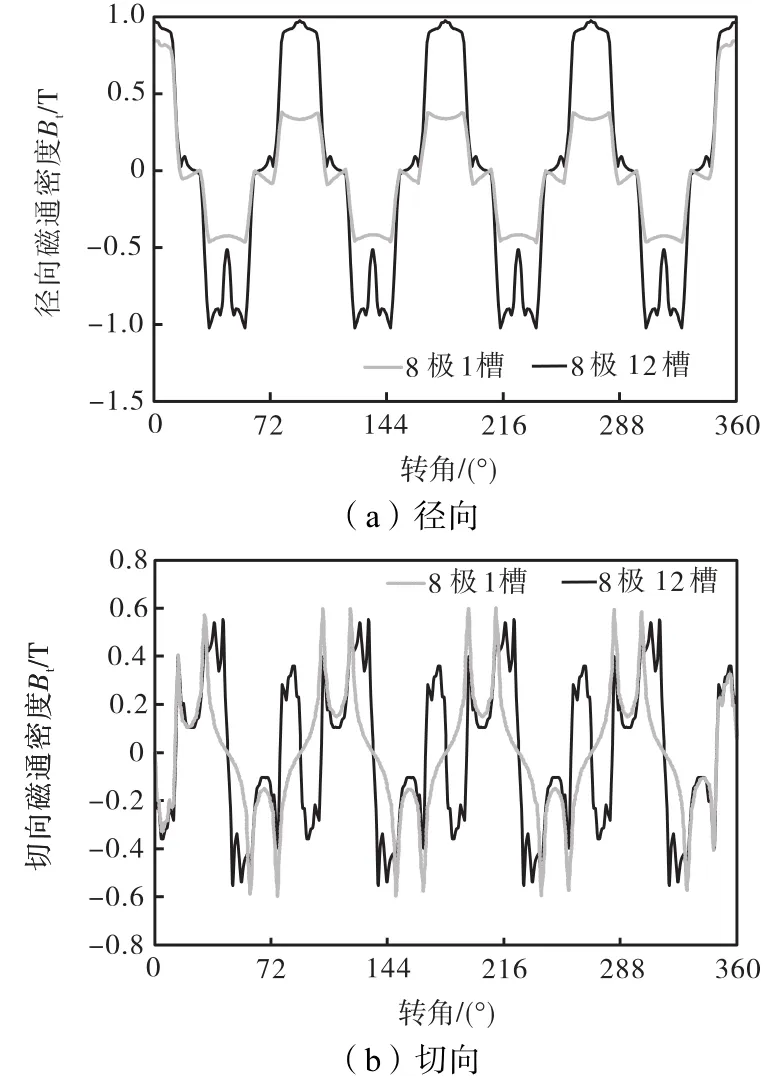
图9 气隙磁通密度(8极12槽)Fig.9 Air-gap magnetic flux density(8,pole/12,slot)

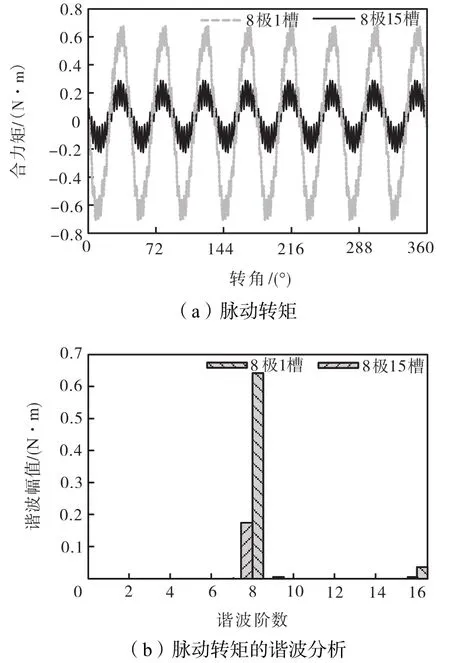
图7 脉动转矩及其谐波分析(8极15槽)Fig.7 Cogging torques and Fourier analysis(8,pole/15,slot)

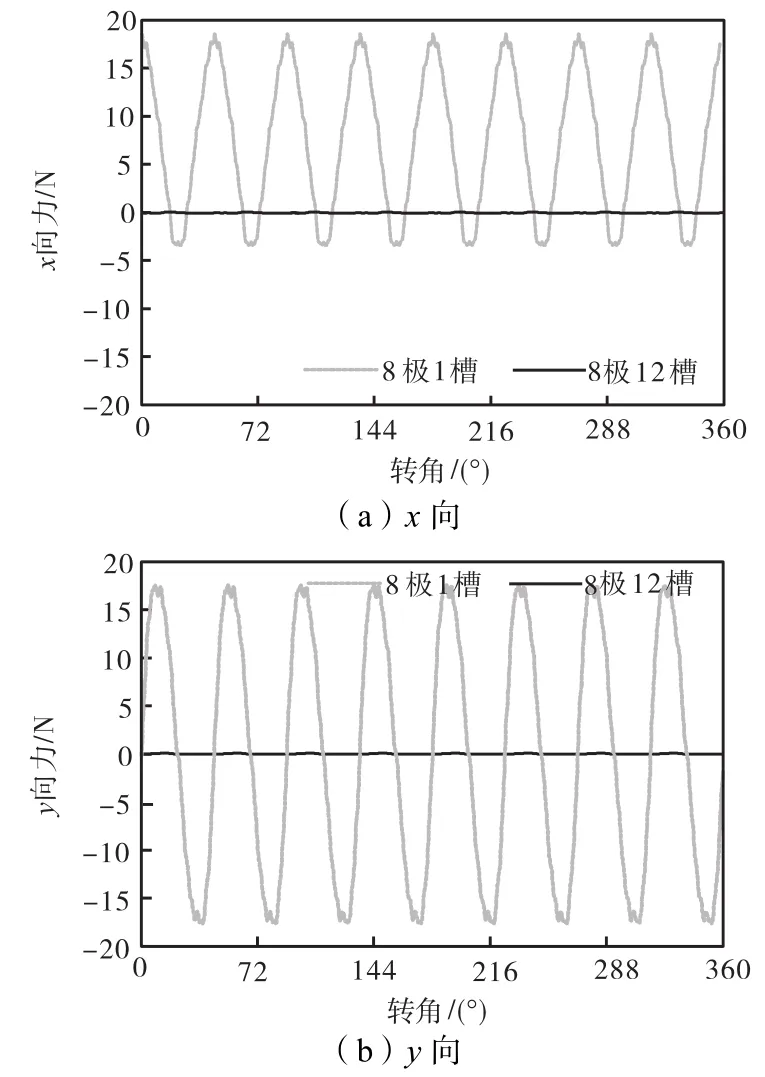
图10 永磁电机不平衡磁拉力(8极12槽)Fig.10 UMP of PM motors(8,pole/12,slot)

2.3 8极12槽电机

图8 为8极12槽电机某一瞬时的磁力线分布，其中图 8(a)和图 8(b)分别对应 8极1槽和 8极 12槽电机．图 9为该瞬时的径向和切向磁通密度．显然，8极12槽电机的磁力线分布更对称．转子每旋转1周，作用于定子齿的磁拉力脉动mN 次．

图 10为电机的径向及切向磁拉力脉动规律．由表 1可知，偶数齿槽应抑制不平衡磁拉力．若忽略计算误差，图10所示不平衡磁拉力为0．

对脉动转矩进一步分析可得图11所示脉动转矩分析结果．由于转子仍然旋转1周，所以第8阶谐波仍为等效基波．8极1槽电机存在等效第1和第2阶谐波，但这两阶谐波在 8极 12槽电机中均受到不同程度的抑制．根据表1所述结论，与等效第1阶和第2阶谐波对应的相位调谐因子分别为8和4，应当抑制脉动转矩．脉动转矩分析由上述分析可见，仿真结果与本文的理论推导一致．

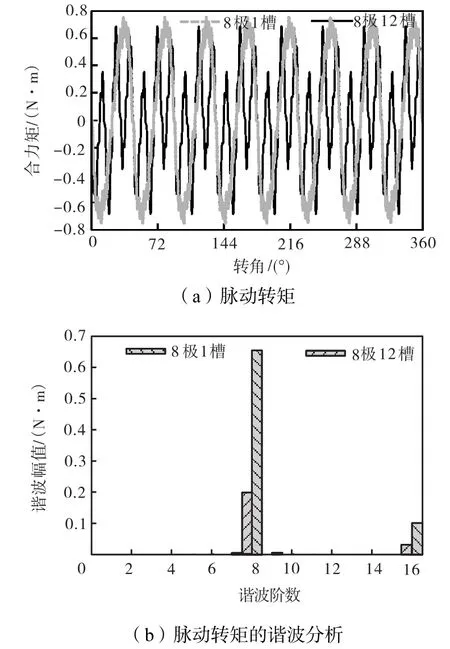
图11 脉动转矩及其谐波分析(8极12槽)Fig.11 Cogging torques and Fourier analysis(8,pole/12,slot)

3 结 论

(1) 揭示了槽极组合与受力特性尤其是 3种典型振动模式之间的映射关系．3种振动模式分别为扭转振动模式、平移振动模式和受力平衡模式．其中，扭转和平移模式分别由脉动转矩和不平衡磁拉力激起，在平衡模式下磁拉力受到完全抑制．

(2) 若槽极最大公因子大于 1，将抑制不平衡磁拉力．该结论与文献[11-12]一致．但应当指出，磁拉力的某些谐波仍可激起转矩脉动，具体情形可采用相位调谐因子进行预测．欲减小转矩脉动，应增加定子齿数，避免出现转矩的低阶脉动谐波激起的显著振动.

(3) 机械及电磁对称是本文工作的基础．由于工程领域存在许多诸如永磁电机和行星传动的旋转对称式,动力/传动系统，因而可采用相位调谐方法研究参数与动态响应之间的映射关系，进而可为动态设计提供技术指导．

［1］ 宋志环，韩雪岩，陈丽香，等. 不同极槽配合永磁同步电动机振动噪声分析[J]. 微电机，2007，40(12)：11-14.

Song Zhihuan，Han Xueyan，Chen Lixiang，et al. Different slot/pole combination vibro-acoustics of permanent magnet synchronous motor[J]. Micromotors，2007，40(12)：11-14(in Chinese).

［2］ 刘 洋，陈丽香，唐任远，等. 永磁同步电动机的振动及噪声实验研究[J]. 电气技术，2009(4)：18-20.

Liu Yang，Chen Lixiang，Tang Renyuan，et al. Test and analysis of vibration and noise for permanent magnet synchronous motor[J]. Electrical Engineering，2009(4)：18-20(in Chinese).

［3］ Kobayashi T，Tajima F，Ito M， et al. Effects of slot combination on acoustic noise from induction motors[J].IEEE Transactions on Magnetics，1997，33(2)：2101-2104.

［4］ 莫会成. 分数槽绕组与永磁无刷电动机[J]. 微电机，2007，40(11)：39-42，81.

Mo Huicheng. Fractional-slot winding and PM brushless motor[J]. Micromotors，2007，40(11)：39-42，81(in Chinese).

［5］ 程树康，葛 新，高宏伟，等. 分数槽永磁直流电动机齿槽定位力矩的研究[J]. 中国电机工程学报，2008，28(21)：10-12，16.

Cheng Shukang，Ge Xin，Gao Hongwei，et al. Research of cogging torque in the brushless DC motor with fractional ratio of slots and poles[J]. Proceedings of the CSEE，2008，28(21)：10-12，16(in Chinese).

［6］ 谭建成. 无刷直流电动机分数槽集中绕组槽极数组合与应用(连载之四)[J]. 微电机，2008，41(3)：52-55.

Tan Jiancheng. Selection of slot／pole number combinations for BLDCM with concentrated windings[J]. Micromotors，2008，41(3)：52-55(in Chinese).

［7］ Hwang C C，Wu M H，Cheng S P. Influence of pole and slot combinations on cogging torque in fractional slot PM motors[J]. Journal of Magnetism and Magnetic Materials，2006，304(1)：e430-e432.

［8］ 韩 力，辛 懋，谢 红，等. 一种模拟实测过程的齿槽转矩数值计算方法[J]. 电机与控制学报，2007，11(6)：589-593.

Han Li，Xin Mao，Xie Hong，et al. Numerical method for calculating cogging torque by simulation of actual measurement[J]. Electric Machines and Control，2007，11(6)：589-593(in Chinese).

［9］ Zhu Z Q，Howe D. Influence of design parameters on cogging torque in permanent magnet machines[J]. IEEE Transactions on Energy Conversion，2000，15(4)：407-412.

［10］ 夏加宽，肖婵娟. 近似极槽无刷直流电动机降低齿槽转矩方法分析[J]. 微电机，2008，41(3)：10-12，16.

Xia Jiakuan，Xiao Chanjuan. Method for reducing cogging torque in PM brushless direct machines with similar slot and pole numbers[J]. Micromotors，2008，41(3)：10-12，16(in Chinese).

［11］ Hanselman D C. Effect of skew，pole count and slot count on brushless motor radial force，cogging torque and back EMF[J]. IEE Proceedings Electric Power Application，1997，144(5)：325-330.

［12］ Bi Chao，Jiang Quan，Lin Song. Unbalanced-magneticpull induced by the EM structure of PM spindle motor[J]. Electrical Machines and System，2005，1(27/28/29)：183-187.

［13］ Chen S X，Low T S，Lin H，et al. Design trends of spindle motors for high performance hard disk drives[J].IEEE Transactions on Magnetics，1996，32(5)：3848-3850.

［14］ 唐任远. 现代永磁电机理论与设计[M]. 北京：机械工业出版社，1997.

Tang Renyuan. Modern Permanent Magnet Machines Theory and Design[M]. Beijing：China Machine Press，1997(in Chinese).

［15］ 王秀和. 永磁电机[M]. 北京：中国电力出版社，2007.

Wang Xiuhe. Permanent Magnet Motors[M]. Beijing：China Electric Power Press，2007(in Chinese).

［16］ Wang Shiyu，Xu Jinyou，Xiu Jie，et al. Elastic wave suppression of permanent magnetic motors by pole/slot combination[J]. ASME Journal of Vibration and Acoustics，2011，133(2)：024501-1-024501-6.

［17］ 张 冉，王秀和，乔东伟，等. 基于辅助槽的永磁电机激振力波削弱方法[J]. 中国电机工程学报，2010，30(8)：103-108.

Zhang Ran，Wang Xiuhe，Qiao Dongwei，et al. Reduction of exciting force wave for permanent magnet motors by teeth notching[J]. Proceedings of the CSEE，2010，30(8)：103-108(in Chinese).

［18］ 张 冉，王秀和，乔东伟. 极弧系数选择对永磁无刷直流电机激振力波的影响[J]. 中国电机工程学报，2010，30(21)：79-85.

Zhang Ran，Wang Xiuhe，Qiao Dongwei. Influence of pole-arc coefficient on exciting force waves of permanent magnet brushless DC motors[J]. Proceedings of the CSEE，2010，30(21)：79-85(in Chinese).

［19］ 王道涵，王秀和，丁婷婷，等. 基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J]. 中国电机工程学报，2008，28(9)：66-70.

Wang Daohan，Wang Xiuhe，Ding Tingting，et al. Optimization for the asymmetric angles of magnetic pole to reduce cogging torque in inner-buried PM brushless DC motors[J]. Proceedings of the CSEE，2008，28(9)：66-70(in Chinese).

［20］ Parker R G. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration[J].Journal of Sound and Vibration，2000，236(4)：561-573.

［21］ Wang Shiyu，Huo Mina，Zhang Ce，et al. Effect of mesh phase on wave vibration of spur planetary ring gear[J]. European Journal of Mechanics-A/Solids，2011，30(6)：280-287.