含裂纹两端铰支输流管道在振荡流作用下的非线性动力特性研究

蔡逢春，臧峰刚，梁艳仙

(1.中国核动力研究设计院 核反应堆系统设计技术国家级重点实验室，成都 610041;2.成都航空职业技术学院 建筑工程系，成都 610021)

两端支承的输流管道在流速足够大的定常流作用下一般只会因屈曲发生静态失稳或称为发散失稳，但是在振荡流的作用下，即使平均流速较小(远小于发生静态失稳的临界流速)，系统也可能因参数共振而动态失稳［1］。Ariaratnam 等［2］采用平均法研究了两端铰支输流管道在振荡流作用下的次谐波共振和组合共振;Namachchivaya等［3］对该系统进行了非线性分析，在共振区域内给出了次谐波共振和组合共振的幅频特性曲线。金基铎等［4］、梁峰等［5］进一步分析了该系统的共振区域内的各种参数共振能够延续的频率范围和它们的振动特性。Panda等［6］采用多尺度法考察了两端铰支输流管道在振荡流作用下的主共振、组合共振和内共振行为。Wang［7］研究了两端铰支输流管道在平均流速较大(大于临界流速)条件下的动力学行为。

含裂纹结构的动力学特性分析一直是个热点研究方向，有大量的文献报道，但关于含裂纹管道的动力学特性的研究较少，Zheng等［8］推导了空心矩形和圆形截面结构横向裂纹在纯弯矩作用下的局部柔度，并研究了其结构的振动特性和稳定性。He等［9］通过将裂纹截面分成一系列的薄环计算管裂纹的应力集中因子和柔度系数，并通过试验验证。这些研究都采用的是开裂纹模型，且没有考虑流体的影响。Yoon等［10］研究了含裂纹简支输流管道在移动载荷作用下的动态特性，其基于Lagrange方程推导出含裂纹两端简支输流管道在移动载荷作用下的运动方程，研究了裂纹对输流管道的频率、位移响应的影响，他们也是假设裂纹在振动过程中始终处于张开状态。

本文首先建立起含呼吸裂纹的输流管道在振荡流作用下的非线性运动方程，采用数值方法，研究含裂纹输流管道在参数共振区域内的运动形态，并与无裂纹输流管道的运动状态相比较，重点考察由于裂纹的存在，导致输流管道的运动形态的改变。

1 裂纹模型

Zheng等［8］通过将含单边直裂纹圆管的裂纹区域分割成为一序列的无限小的矩形条带区域，各个微小裂纹条带的应力强度因子近似使用无限长板条的单变裂纹应力强度因子，然后求得直裂纹的柔度系数。本文基于其方法建立管道外壁部分圆周裂纹(如图1所示)的柔度系数。裂纹深度为a，裂纹对应的圆心角为2θ，管壁厚度为 h，管外径为 De，内径为 Di。

积分条带处的应力强度因子为［8］:

在纯弯矩作用下由外壁部分圆周裂纹带来的局部柔度系数为:

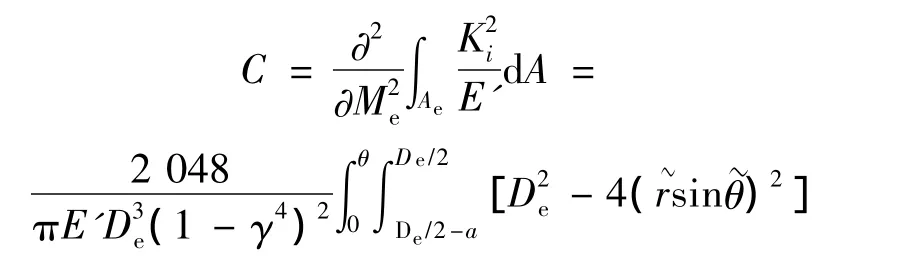
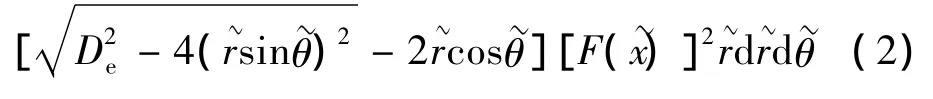
式中，E'=E/(1－ν2)，E为弹性模量，ν泊松比，Ae为裂纹区域。

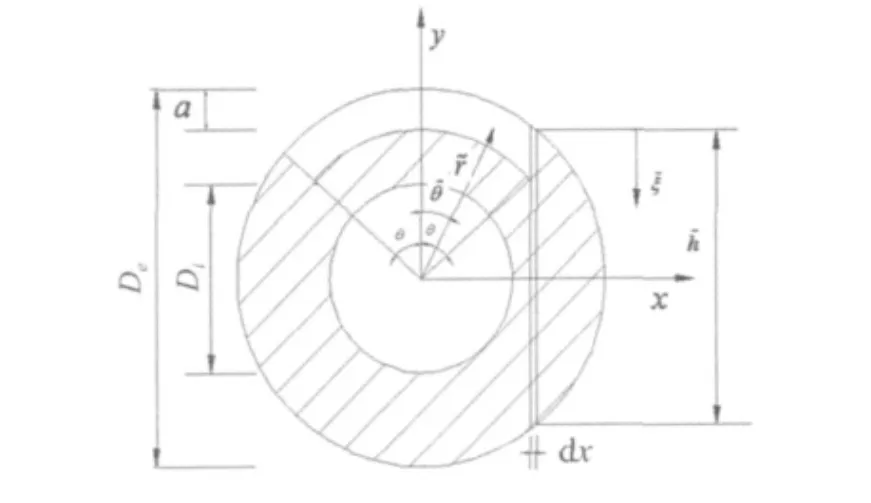
图1 外壁部分圆周裂纹Fig.1 Partly circumferential crack

2 纹梁的模态函数

含裂纹梁在裂纹处转角不连续，为了得到满足边界条件和裂纹处的不连续条件的模态函数，本文通过在不含裂纹梁的模态函数中加入3次多项式来构造出含裂纹梁的模态函数。

依据模态假设法，梁的横向位移可以写成:

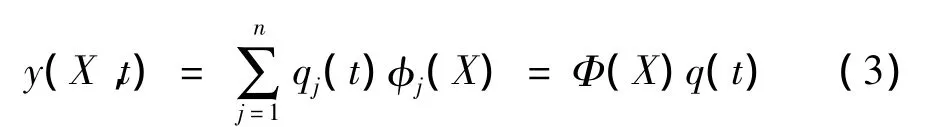
考虑含有Q－1条裂纹的梁，裂纹梁被分成Q段，分别用扭转弹簧组装起来。设含裂纹梁的第k段的第j阶模态函数为:

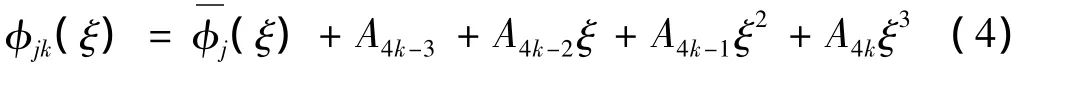
式中，ξ∈［ξkξk+1］，ξ=X/L，L 为管道长度，两端点坐标，ξ1=0，ξQ+1=1，A4k－3～A4k为待定系数，(ξ)无裂纹梁的模态函数，k=1，2，…，Q。

对于两端铰支梁，有以下4个边界条件:

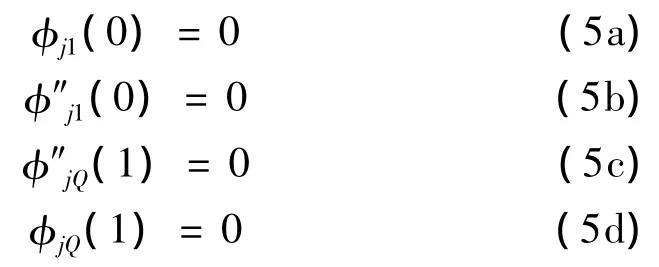
在裂纹处要满足位移、转角、剪力和弯矩4个协调条件:

式中，Ck－1为裂纹柔度系数，(')= ∂/∂ξ，k=2，3，…，Q。

通过式(5)、式(6)可唯一确定含裂纹梁的模态函数。

3 含裂纹两端铰支输流管道运动方程

3.1 输流管道模型

含裂纹两端铰支输流管道的模型见图2，输流管道长度为L，流体横截面积为A，管道横截面积Ap，单位长度管道的质量为m，抗弯刚度为EI，流体的相对管道流速为U，单位长度流体的质量为M，裂纹位置为Xc，裂纹为外壁部分圆周裂纹，管道沿着X轴方向放置如图2。对管道和流体有以下基本假设:① 裂纹尖端应力在弹性范围内;② 流体无粘性、不可压缩;③ 管道内流速U一致;④ 管道在平面内运动;⑤ 采用Euler梁假设，不计管道的转动惯量和剪切变形。

初始状态，物质点的坐标采用Lagrange坐标(X，Y)描述，变形后采用Euler坐标(x，y)描述，物质点的位移为 u=x－X，v=y－Y。

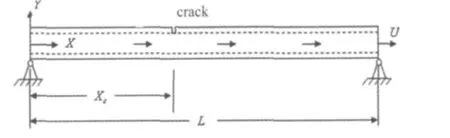
图2 含裂纹两端铰支输流管道模型Fig.2 A hinged-hinged pipe conveying fluid with a crack

3.2 用于描述输流管道运动的拉格朗日方程

Stangl［12］应用一种适用于含有非材料体(non-material volumes)系统的 Lagrange方程［11］推导出了悬臂输流管道的非线性运动方程，这种扩展的Lagrange方程非常方便处理流进流出控制体的质量。本文基于此方程来推导含裂纹输流管道系统的运动方程。其运动方程可写为:

式中，T为系统的总的动能，Qi为系统的广义力，qi为广义坐标。方程中包含两个曲面积分，用于描述流入流出控制体的质量。Γ为控制体的边界，da描述曲面Γ上的微元方向，VF、VP分别是流体的速度和管道的速度,是单位体积流体的动能。

3.3 系统的动能

对于两端铰支输流管道，在发生横向位移后，由于两端的位移为零，管道的伸长将导致管道的横截面积缩小，当流体为不可压缩时，管道横截面积的缩小将导致流速增大，考虑了这些因素后，Paidoussis在其文献［1］中给出了流体的速度矢量为:

式中，(')=∂/∂X，()=∂/∂t。

对于两端铰支输流管道，忽略高阶项，系统动能可写成［1］:

式中，Tp为管道动能，TF为流体动能。

3.4 曲面积分

依据前面的分析，流体的单位体积动能可写成:)

式中，ρF为流体密度。

由于在裂纹处的转角不连续，因此在裂纹截面左右两边的方向矢量不相等。在裂纹截面左右两边的曲面积分的和也不等于零。在裂纹截面左边的曲面积分为:

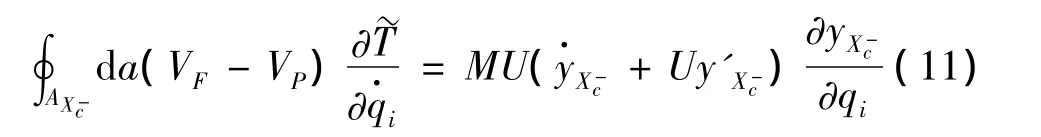
裂纹截面右边曲面积分为:

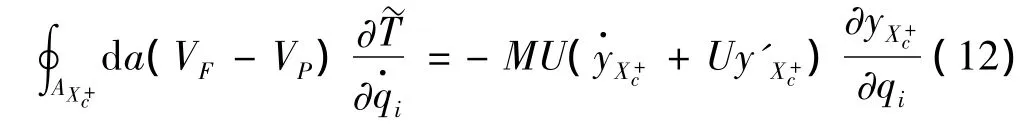
由裂纹处的协调条件(6)，裂纹左右两边的曲面积分式(11)、式(12)的和为:

由于VF－VP=U，广义速度项无关为变形后管道切向方向矢量，因此方程(7)中的第二个曲面积分等于零。

3.5 广义力

由弯曲变形引起的弹性势能为:

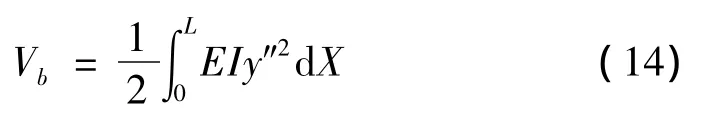
用于模拟裂纹的无质量弹簧的势能为:

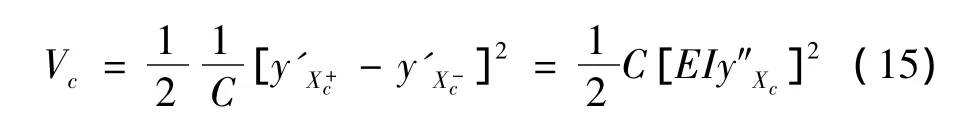
考虑管道的横向运动产生附加的轴向力，输流管道的横截面轴力和流体压力可表示为［1］:

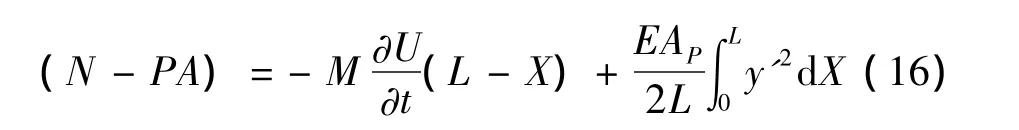
式中，N为管道轴力，P为流体压力。管道轴力和流体压力做的功:

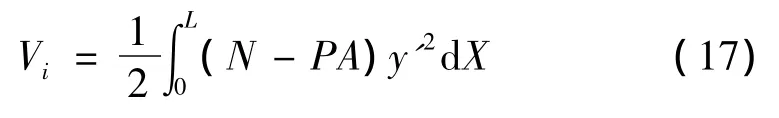
因此可以得到广义力为:

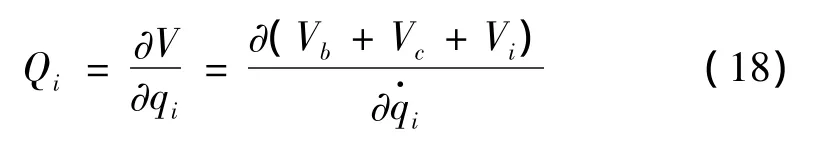
3.6 系统运动方程

为了得到无量纲运动方程，引入以下无量纲量:

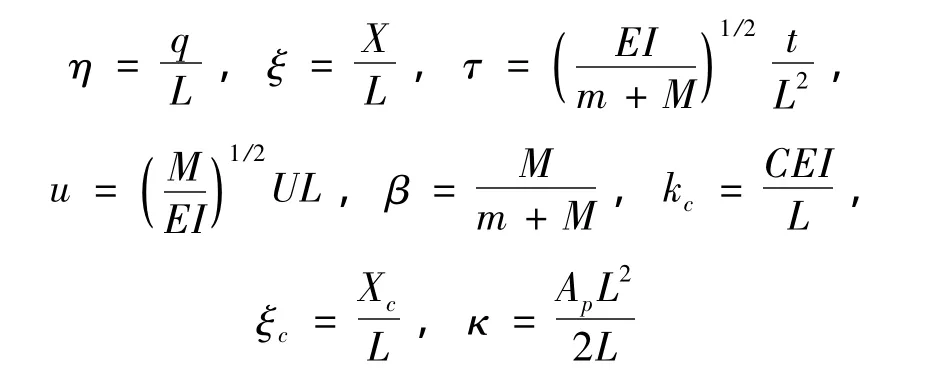
考虑无量纲流速为:

式中，u0为平均流速，Ω为振荡流频率，μ为振荡流幅值。

将以上得到的系统动能、曲面积分和广义力代入方程(7)，且考瑞利阻尼比例系数，可得到裂纹张开时，系统无量纲运动方程的质量、阻尼、刚度矩阵为:

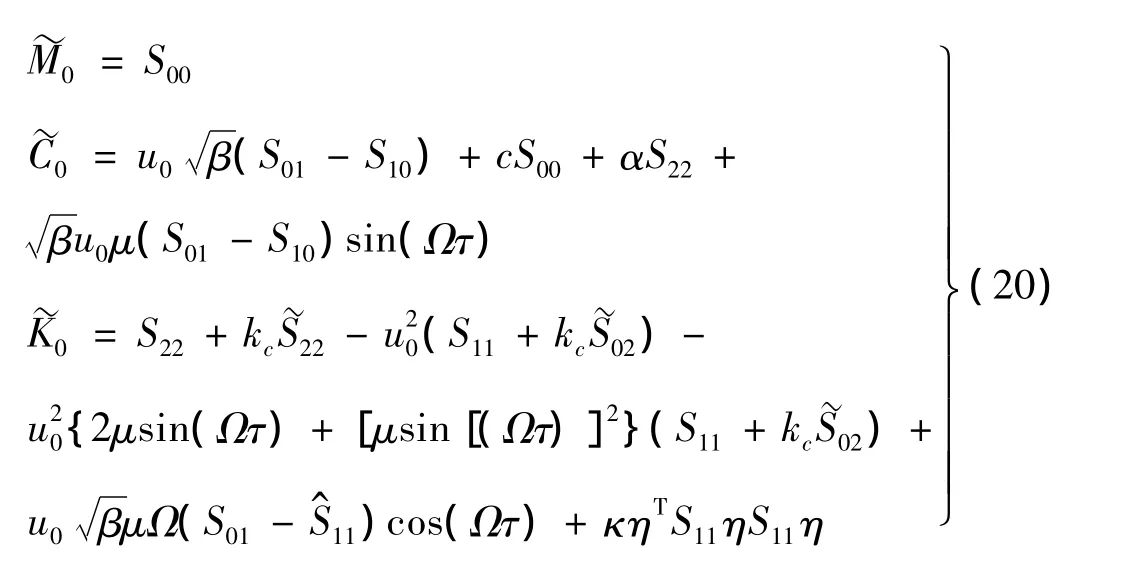
式中:

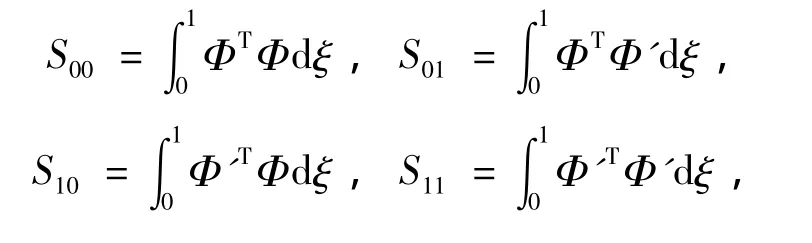
当裂纹闭合时，裂纹带来的局部柔度系数C=0，此时含裂纹输流管道的运动方程与无裂纹输流管道的运动方程是一样的，令C=0，类似式(20)，可以求得裂纹闭合状态时，系统的质量矩阵、阻尼矩阵、刚度矩阵。

裂纹的张开闭合状态将由裂纹处的曲率η″(ξc)的正负号来确定，含呼吸裂纹两端铰支输流管道的运动方程可写成:

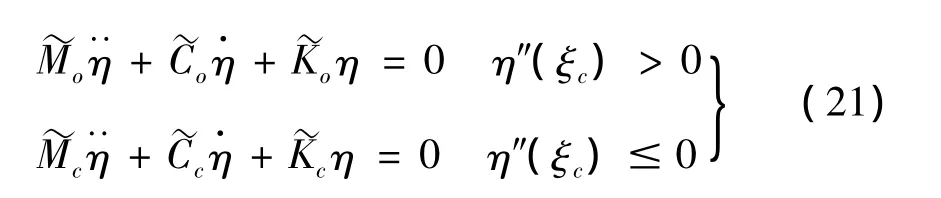
式中，(')=∂/∂ξ，()=∂/∂τ。

可以看出，由于裂纹张开、闭合，含呼吸裂纹的输流管道的质量矩阵、阻尼矩阵和刚度矩阵将随裂纹的张开闭合状态的变化而改变。

4 数值计算与分析

本节将采用龙格库塔法对方程(21)直接积分，研究有/无裂纹输流管道在振荡流作用下的运动特性，重点考察由于裂纹的存在会对输流管道的运动形态的改变。

4.1 无裂纹输流管道在振荡流作用下的参数共振

为验证本文所建立的含裂纹输流管道在振荡流作用下的运动方程的正确性，首先研究无裂纹输流管道非线性行为，并与已有文献［3－4］比较，取系统参数与文献［4］相同，为:α =0.005、c=0、β=0.64、μ=0.4、κ=5 000、u0=2.5。取2阶模态函数进行数值计算［5，6］，计算结果如图3所示。图中的横坐标为振荡流无量纲频率Ω，纵坐标为管道中点位移幅值，当管道中点的运动速度为零的时候，记录此时中点的位移值。

从分岔图可以看出，当0＜Ω＜6时，系统主要表现为混沌运动，还包含了一些周期运动，这以区域主要是系统一阶振型主共振和超谐共振区域;区域6.9＜Ω＜16.1对应于系统的一阶振型1/2次谐波共振区域，振幅随激励频率的增加而增大，当6.9＜Ω＜10时，系统表现为复杂的周期1运动，当10＜Ω＜16.1时，系统进入周期1运动。区域35＜Ω＜53.2对应于系统的一、二阶振型组合共振区域，振幅随激励频率的增加而增大，当35＜Ω＜40.3时，系统表现为周期运动或拟周期运动，当40.3＜Ω ＜53.2时，系统进入周期1运动;区域64＜Ω＜94.6对应于系统的二阶振型1/2次谐波共振区域，振幅随激励频率的增加而增大，系统表现为周期1运动。在其它区域内，系统处于稳定状态。出现的这些运动形态以及失稳区域与文献［4］是一致的。

为更清楚描述系统的运动状态，图4给出了几个典型运动形态的相图与相应的Poincare映射图。Poincare映射图采用类似文献［13］中给出的映射触发器:当管道位置ξ=0.3处位移为零时，记录ξ=0.7处的运动状态。由于在记录时没有区分速度的正负，周期1运动有2个孤立点，见图4(d)，拟周期运动在Poincare映射图上点组成两个封闭环，见图4(c)，混沌运动，有无穷多个离散点，见图4(a)。

4.2 含裂纹输流管道在振荡流作用下的分岔与混沌行为

取参数:管长L=1 m，外径 De=0.1 m，内径 Di=0.07 m，弹性模量 E=2.0 ×108Pa，泊松比 ν=0.36，裂纹角 θ=π/2，裂纹相对深度 a/h=0.9，裂纹位置 ξc=0.3，α =0.005、c=0、β =0.64、u0=2.5。取2 阶模态函数进行数值计算，计算结果如图5所示。作分岔图的方法与4.1节相同。

从分岔图可以看出，当0＜Ω＜6.1时，系统主要表现为混沌运动和周期运动，与不含裂纹的输流管道的运动状态类似;区域6.8＜Ω＜15.9对应于系统的一阶振型1/2次谐波共振区域，振幅随激励频率的增加而增大，在这一区域明显存在一个与无裂纹输流管道不同的地方，由于裂纹的存在，输流管道分岔图上出现了经过多个倍周期分岔进入混沌运动，又通过多个倍周期分岔从混沌运动进入周期运动(见图5(b))。当40.6 ＜Ω ＜49.8，系统进入一、二振型组合共振区域，系统的运动形态存在明显的跳跃，即在某些参数处系统的运动形态可能从一种形态突然改变到另外一种形态，系统主要表现为周期运动，且由于裂纹的存在使得拟周期运动消失了;当62.6＜Ω＜93.3，系统进入二阶振型1/2次谐共振区域，系统表现为混沌运动，这与无裂纹输流管道的运动状态完全不同，这些不同是由于裂纹存在造成的。在其它区域，系统稳定，位移幅值最终收敛于零。

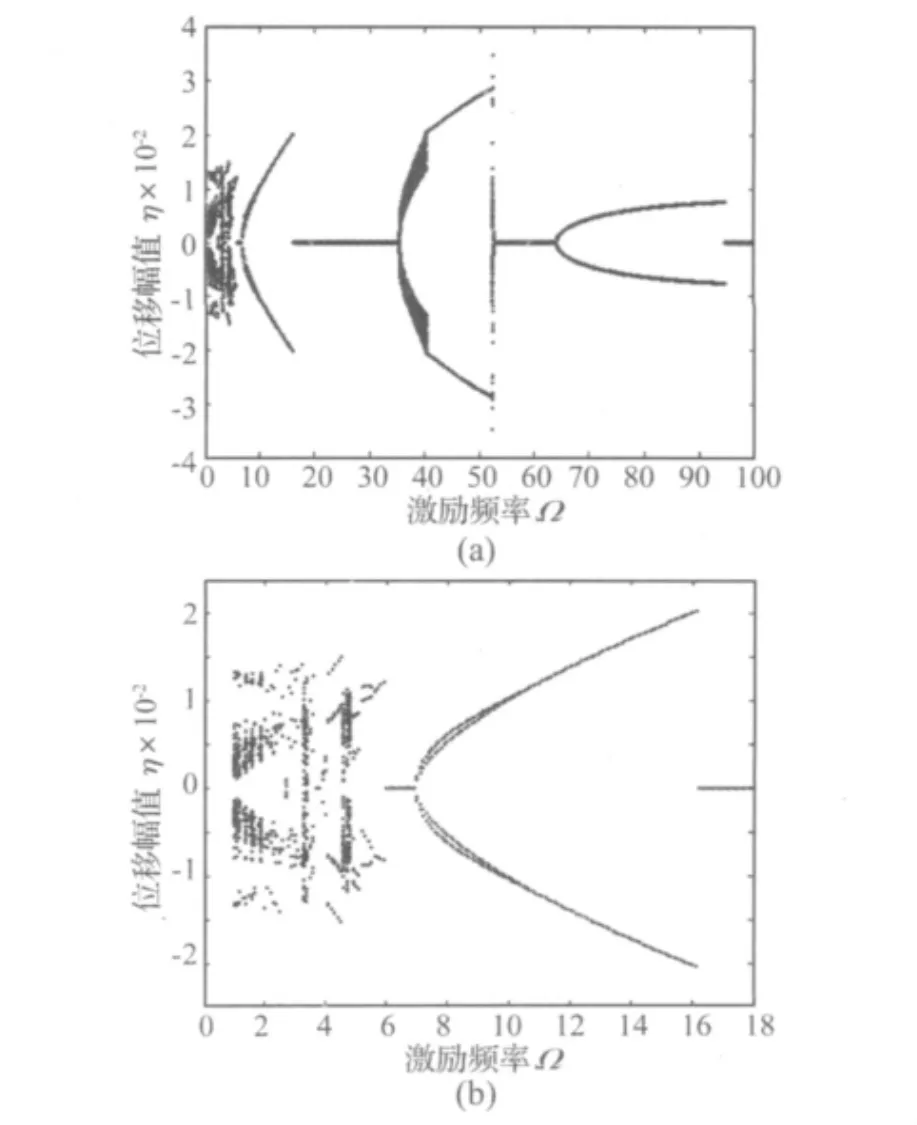
图3 无裂纹输流管道分岔图Fig.3 Bifurcation diagram for a uncracked pipeconveying fluid

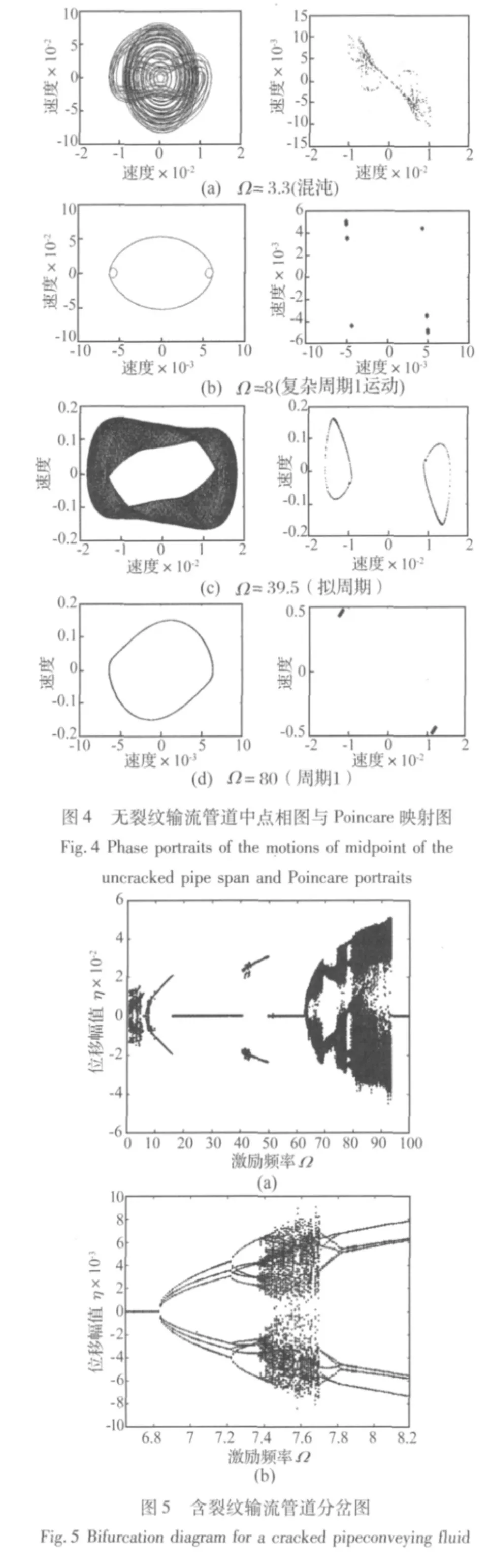
为更清楚描述系统的运动状态，图6给出了几个典型运动形态的相图和相应的Poincare映射图，采用的映射触发器与4.1节相同。Ω=7.3时，为复杂的周期1运动，见图6(a);Ω=7.3时，系统表现为复杂的周期2运动，见图6(b);Ω =7.5、85时，Poincare映射图上有无穷多个点，为混沌运动，见图6(c)、图6(d)。

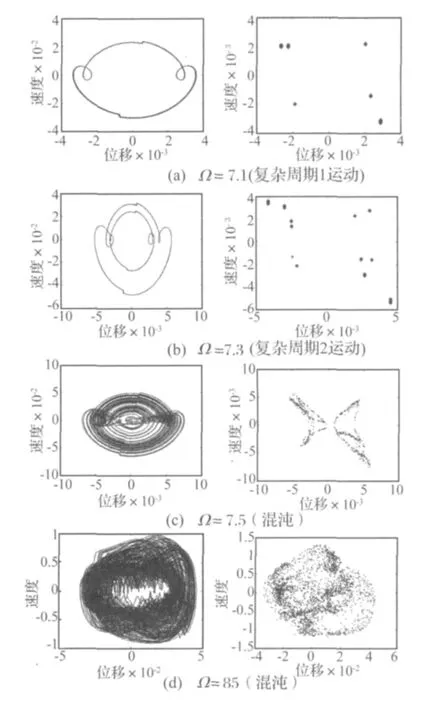
图6 含裂纹输流管道中点相图与Poincare映射图Fig.6 Phase portraits of the motions of midpoint of the cracked pipe span and Poincare portraits

4.3 裂纹深度的影响

通过以上对含裂纹输流管道在振荡流作用下的运动状态的研究，发现由于呼吸裂纹的存在，会导致输流管道的运动状态由周期运动变为混沌运动。为详细研究裂纹对输流管道运动状态的影响，下面通过数值计算，以裂纹相对深度为分岔参数作分岔图，图7、图8分别为激励频率Ω=7.5、Ω=85时，以裂纹相对深度为分岔参数所得到的分岔图，其它参数与4.2节相同。从图7可以看出，当激励频率Ω=7.5时，随着裂纹深度的增加，系统通过多个倍周期分岔进入混沌运动，且随着裂纹深度的增加，分岔图保持连续性。当激励频率Ω=85时，从分岔图(图8)可以看出系统的运动形态存在明显的跳跃，振动幅值发生骤然的变化，裂纹相对深度较小时，系统表现为周期1运动，裂纹相对深度较大时，系统主要表现为混沌运动。

5 结论

基于本文建立的含裂纹输流管道在振荡流作用下的非线性运动方程，采用数值方法，研究了有/无裂纹的输流管道在振荡流作用下的参数共振。

对于无裂纹输流管道，研究表明:在一、二阶振型1/2次谐波共振区域及组合共振区域出现的运动形态与已有相关文献的结论是一致的，证明本文建立的运动方程是正确的。本文还发现，激励频率较小条件下(一阶振型超谐共振区域)，系统发生了混沌运动和周期运动。

对于含裂纹输流管道，结果表明，含裂纹输流管道表现出更丰富的动力学行为。在一阶振型1/2次谐波共振区域，系统运动形态通过典型的倍周期分岔进入混沌运动，又从混沌运动经过倍周期分岔进入周期运动;在一、二阶振型组合共振区域，系统的运动形态存在明显的跳跃，对应的振幅也有骤然的变化，在这一区域系统主要表现为周期运动，且由于裂纹的存在，拟周期运动消失。在二阶振型1/2次谐波共振区域，系统表现为混沌运动。

最后研究了含裂纹输流管道在振荡流作用下的运动形态随裂纹相对深度的变化，研究表明:当激励频率Ω=7.5时，随着裂纹深度的增加，系统通过多个倍周期分岔进入混沌运动，当激励频率Ω=85时，随着裂纹深度的变化，系统的运动形态存在明显的跳跃。

［1］ Paidoussis M P.Fluid-structure interactions，slender structures and axial flow［M］.Academic Press，San Diego，1998.

［2］ Ariaratnam S T，Namachchivaya N S.Dynamic stability of pipes conveying pulsating fluid［J］.Journal of Sound and Vibration，1986，107:215－230.

［3］ Namachchivaya N S.Non1inear dynamics of supported pipe conveying pulsating fluid.1.sub-harmonic resonance and 2.combination resonance［J］.International Journal of Nonlinear Mechanics，1989，24:185－208.

［4］ 金基铎，杨晓东，尹 峰.两端铰支输流管道在脉动内流作用下的稳定性和参数共振［J］.航空学报，2003，24(4):317－322.

［5］ 梁 峰，杨晓东，闻邦春.脉动流激励下输流管道参数共振IHB方法研究［J］.振动与冲击，2008，27(9):44－46.

［6］ Panda L N，Kar R C.Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances［J］.Journal of Sound and Vibration，2008，309:375－406.

［7］ Wang L.A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid［J］.International Journal of Nonlinear Mechanics，2009，44:115－121.

［8］ Zheng D Y，Fan S C.Vibration and stability of cracked hollow-sectional beams［J］.Journal of Sound and Vibration，2003，267:933－954.

［9］ He Y，Ye J，Chen X，et al.Discussion on calculation of the local flexibility due to the crack in a pipe［J］.Mechanical Systems and Signal Processing，2009，23:804－810.

［10］ Yoon H I，Son I S.Dynamic behavior of cracked simply supported pipe conveying fluid with moving mass［J］.Journal of Sound and Vibration.2006，292:941－953.

［11］ Irschik H，Holl H J，The equations of lagrange written for a non-material volume［J］.Acta Mechanica，2002，153:231－248.

［12］ Stangl M，Gerstmayr J，Irschik H.An alternative approach for the analysis of nonlinear vibrations［J］.Journal of Sound and Vibration，2008，310:313－325.

［13］ 王 琳.输流管道的稳定性、分岔与混沌行为研究［D］.武汉:华中科技大学，2006.