变摩擦TMD特性和简谐激励控制效果的研究

秦 丽，闫维明，郭声波

(1.襄樊学院 建筑工程学院，湖北 襄樊 441021;2.北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100022)

调谐质量阻尼器(TMD)安装时不需修改结构，可直接安装在结构顶层，因其灵活方便，众多学者研究了TMD的控制效果和设计方法［1－2］。常见TMD系统采用粘滞阻尼，是固体在液体中运动产生的一种阻尼，构造比较复杂，而且粘滞阻尼系数在实际制作中有时很难满足要求。摩擦力可以由重物滑动、结构结点转动等产生，比较容易实现，而且造价低廉，用于TMD能有效降低其造价。鉴于摩擦TMD的优点和潜在的应用前景，不少学者对摩擦TMD的特点和规律进行了研究。文献［3］采用随机线性化方法研究了采用摩擦阻尼器的TMD，结果证明这种非线性TMD只要正确设计，其控制效果可以和线性阻尼TMD相媲美。田志昌等［4－5］在被动调谐质量阻尼器系统中采用摩擦耗散能量，以替代粘滞阻尼，讨论了这种新系统最优参数问题，并利用数值仿真说明了新方法的减振效果稳定。闫维明等申请了悬吊式摩擦TMD的专利［6］，并将其应用于实际工程［7］。但摩擦元件是非线性元件，数值模拟较为复杂，与粘滞阻尼器相比，增加了TMD分析的难度;另外，摩擦阻尼器的滞回模型大都类似矩形，存在一个临界值(起滑力)，当荷载超过该值以后，装置开始滑动，滑动时其刚度变为0，摩擦力大小不变。由于常摩擦阻尼器滞回模型的特点，常摩擦TMD在外部激励小时不启动，在外部激励大时又不能提供足够的阻尼，为了最大限度发挥其控制效果，选择一个合适的起滑力至关重要，这必然增加摩擦TMD设计的复杂性。

针对常摩擦TMD的缺点，本文提出一种变正压力式变摩擦装置，通过改变摩擦面正压力实现摩擦力随TMD位移增大而增大。分析了变摩擦单自由度系统的动力特性，变摩擦TMD－主结构系统的频率响应特性，进行了变摩擦TMD在简谐荷载作用下对结构响应控制效果的理论分析和实验研究。

1 变正压力式变摩擦TMD工作原理

Whiteman和 Ferri［8］研究了具有位移依赖型摩擦阻尼器的悬臂梁在简谐激励下的运动特性，详细分析了系统滑动－静止的运动特征。本文借鉴文献［8］通过改变摩擦面正压力来实现改变摩擦力的思想，提出变正压力式变摩擦TMD，其原理如图1所示，特点是采用变摩擦装置代替传统TMD中的油阻尼器。变摩擦阻尼器由斜面、摩擦块、摩擦面、弹簧和滚动轴承组成。摩擦阻尼由摩擦块和摩擦面之间的摩擦力提供。摩擦块和TMD质量在TMD运动方向不能产生相对运动，保证摩擦块在摩擦面上的运动与TMD运动一致性。在垂直于TMD运动方向，摩擦块和TMD质量可以自由地相对运动，保证正压力全部传到摩擦面上，不会传到TMD质量上。变摩擦装置弹簧只能在弹簧长度方向伸缩，不能在垂直于弹簧长度方向变形，弹簧一端与摩擦块相连，另一端连接一个滚动轴承，滚动轴承和斜面接触。当TMD左右运动时，带着摩擦块、弹簧和轴承一起运动，由于轴承和斜面接触，弹簧压缩量随着TMD位移的变化而变化，正压力也发生变化，摩擦力自然就会随位移增大而线性增大。

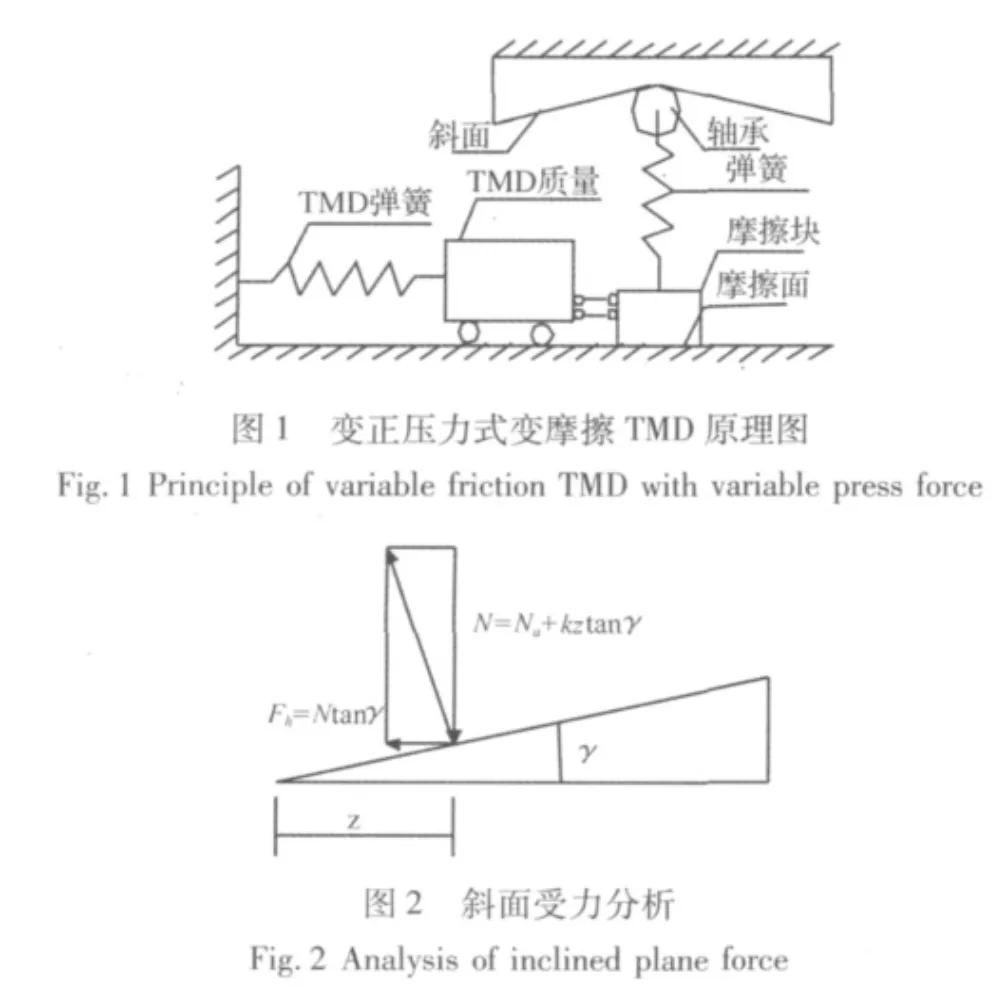
图2给出了斜面的受力分析，弹簧对斜面的压力N=N0+ktztanγ，N0是弹簧的预压力，kt为弹簧刚度，z是TMD的位移，γ是斜面的倾角。竖向弹簧力也就是摩擦块的正压力。在竖向弹簧压力的作用下，斜面产生垂直与斜面的反力，此反力会有水平方向的分力，Fh=Ntanγ，这个水平分力可以作为TMD的恢复力，可见这种变摩擦装置不仅提供摩擦力，还会改变系统的频率。

2 变摩擦单自由度系统动力特性

2.1 变摩擦单自由度系统动力特性理论推导

为了分析变摩擦TMD的阻尼和刚度特性，先分析变摩擦单自由度系统的动力特性。变正压力式变摩擦单自由度系统在简谐激励下的运动方程为:

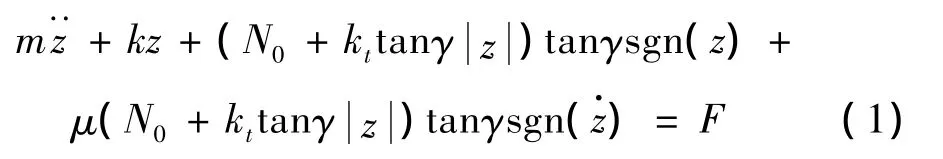
其中，m，k是单自由度系统质量和刚度;N0为弹簧初始压力，kt为弹簧刚度;γ为斜面的角度;μ是摩擦面的摩擦系数;分别为系统的加速度，速度和位移;F是简谐激励。

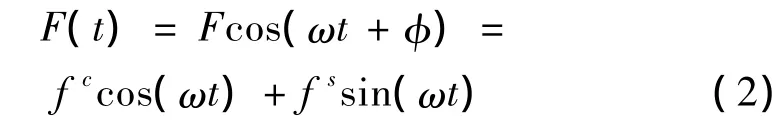
将式(1)中的非线性项展开成傅里叶级数，并取第一项，得到以下的近似:

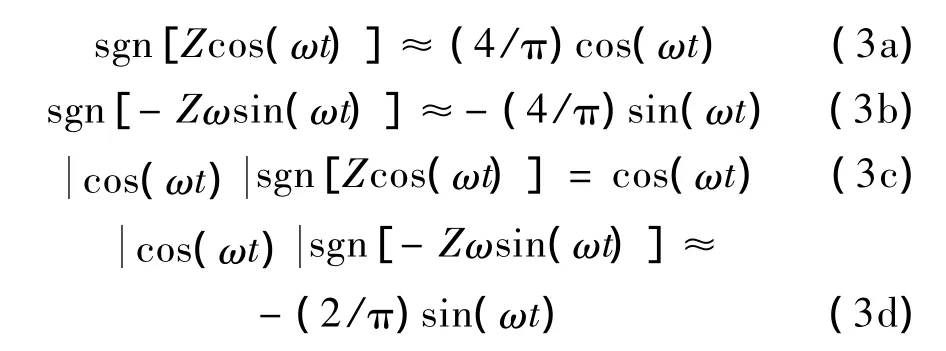
将式(2)、式(3)代入式(1)中，并分别平衡正弦和余弦项，得:

其中:

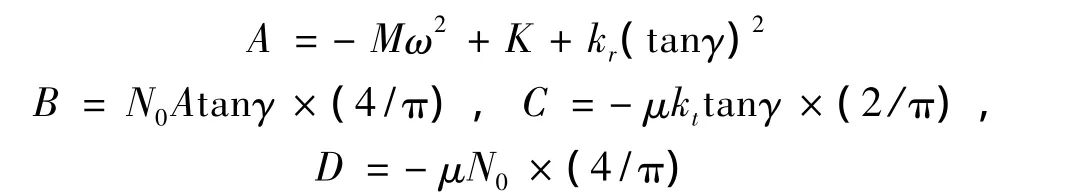
利用式(4)，并考虑 F2=(fc)2+(fs)2，得:

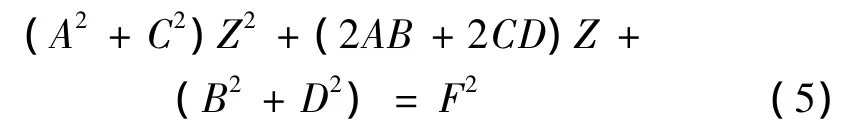
解式(5)这个一元二次方程，得:

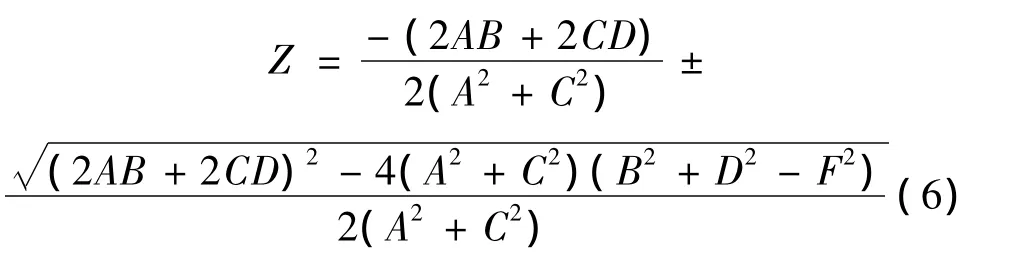
由式(6)可求出变摩擦单自由度系统在幅值不变、频率变化的简谐荷载作用下响应幅值随激励频率的变化曲线，从而得到系统的频响特性。变摩擦单自由度系统的响应和激励之间的相位差可以通过下式求出:

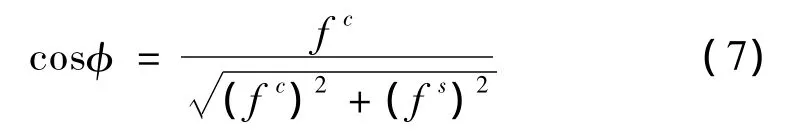
为了得到变摩擦系统的等效阻尼比和等效频率，给出线性阻尼系统谐波平衡公式:

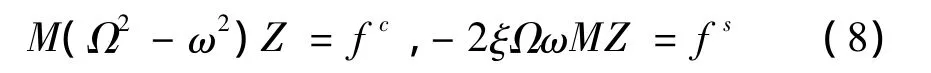
通过比较式(8)和式(4)，可以得到等效频率和等效阻尼比:

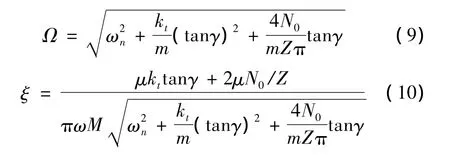
2.2 系统参数对等效阻尼比和等效刚度的影响

通过算例来分析变摩擦单自由度系统等效阻尼比和等效频率的变化规律。

算例1单自由度系统，m=21.5 ton，k=3 013 kN/m，斜面角度:5、10、15、25、35。摩擦面正压力施压弹簧刚度 kt:12 500 kN/m、17 500 kN/m、25 000 kN/m。初始预压力:25 kN、50 kN、100 kN、150 kN、200 kN。摩擦面摩擦系数0.1。

图3给出了N0=100 kN，γ=15°时弹簧刚度对系统等效阻尼和等效刚度的影响，可以看出二者都随弹簧刚度的增大而增大。从图中还可以看到等效阻尼比在TMD运动幅值很小时随系统运动幅值增大而减小，原因在于，运动幅值很小时摩擦力主要由大小不变的预压力产生，所以变摩擦系统也体现了常摩擦系统特点，即阻尼比随运动幅值增大而减小。系统达到一定运动幅值后，斜面引起的弹簧压缩所产生的正压力远远超过预压力，此时变摩擦系统体现出了线性阻尼系统的特点，即阻尼比不随运动幅值的改变而改变。

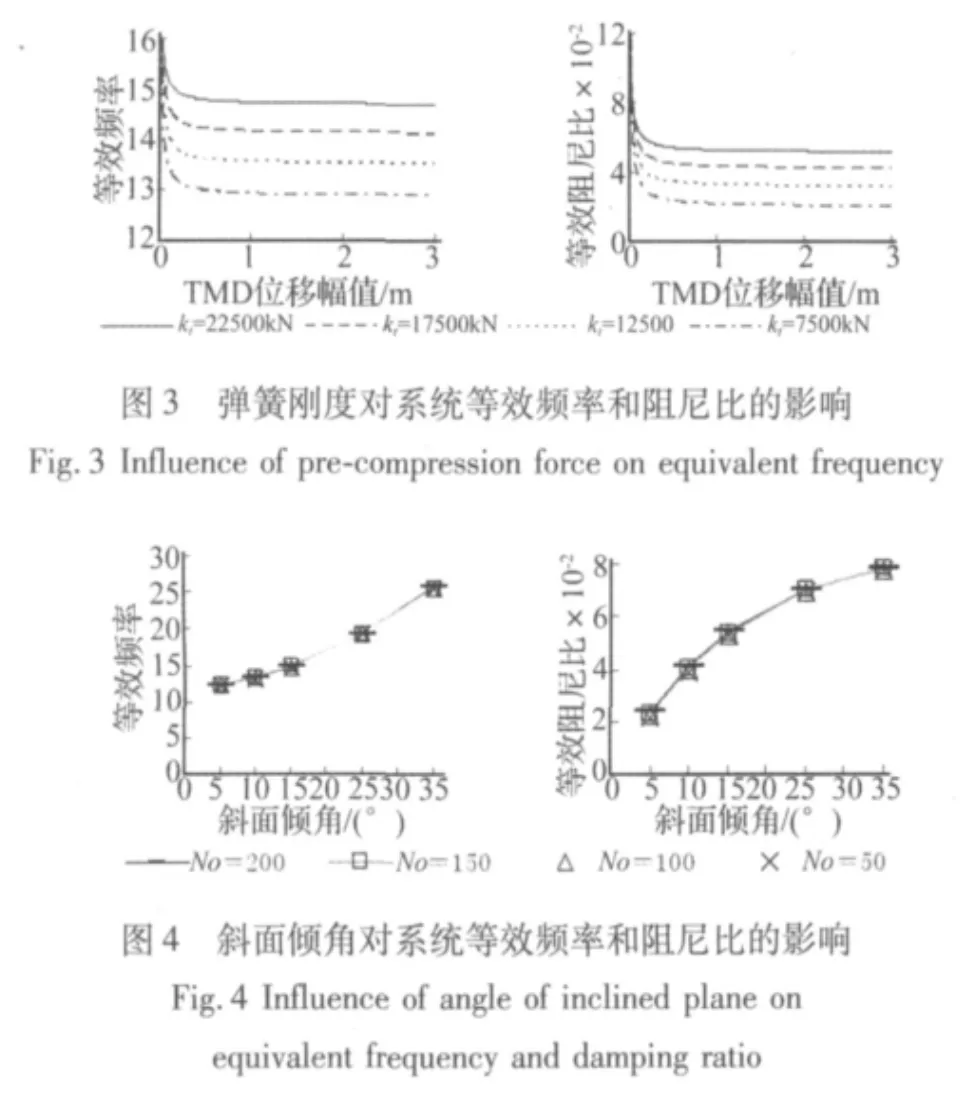
图4给出了斜面倾角对系统等效阻尼比和等效频率的影响。可以看到，二者都随倾角增大而增大。具体地，倾角从5°增大到10°时，等效频率和等效阻尼比分别增大了8%和82%;10°到15°时，增大了11.7%和36%;15°到 25°时，增大了 30.7% 和 30%;25°到 35°时，增大了33.2%和12%。总的来说，倾角越大，增大倾角对阻尼比的增大效果越不明显，而对增大频率的效果越明显。从图4中还可以看到，等效频率和等效阻尼随斜面倾角的变化曲线几乎与预压力无关。事实上，代表不同预压力的四条曲线几乎是重合的。这些情况在系统设计中应加以考虑。

图5给出了kt=22 500 kN/m，倾角为15°时不同预压力(N0在50～200 kN变化)下，等效阻尼比和等效刚度随系统运动幅值变化而变化的趋势。从图中可以看到，预压力只在TMD运动幅值很小的时候对等效阻尼比和等效刚度有一定的影响。还可以看出弹簧预压力对等效阻尼比的影响稍大于它对等效频率的影响。

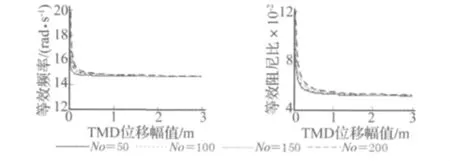
图5 弹簧预压力对系统等效频率和阻尼比的影响Fig.5 Influence of pre-pressure on equivalent frequency and damping ratio

2.3 变摩擦单自由度系统的频率响应特性

通过算例研究变摩擦单自由度系统的频率响应特性，并和它的等效线性阻尼系统作比较。

算例2单自由度系统，m=21.5 ton，k=1 500 kN/m，kt=17 500 kN/m，N0=0，摩擦系数 μ=0.1，斜面倾角15°。按式(9)和式(10)计算等效频率 ωe=11.726，等效阻尼比 ξe=0.05，相应的经典阻尼系统参数为:me=21.5 ton，ke=ω2e× me=2 956.23 kN，ξe=0.05。

图6(a)比较了变摩擦单自由度系统和它的等效线性系统在幅值不变(F=21.5 kN)，频率改变的简谐激励作用下，位移响应幅值随激励频率的变化曲线。可以看到，变摩擦系统的稳态位移响应幅值在共振频率附近比它的等效线性系统的略大，但二者总体趋势接近。图6(b)给出了变摩擦单自由度系统和等效系统相位角余弦随激励频率的变化曲线，可以看到，二者只是稍有差别。

因此在设计变摩擦系统的参数时，可以先按经典阻尼的理论进行计算，然后再在适当折减阻尼比的条件下设计变摩擦系统的相关参数。

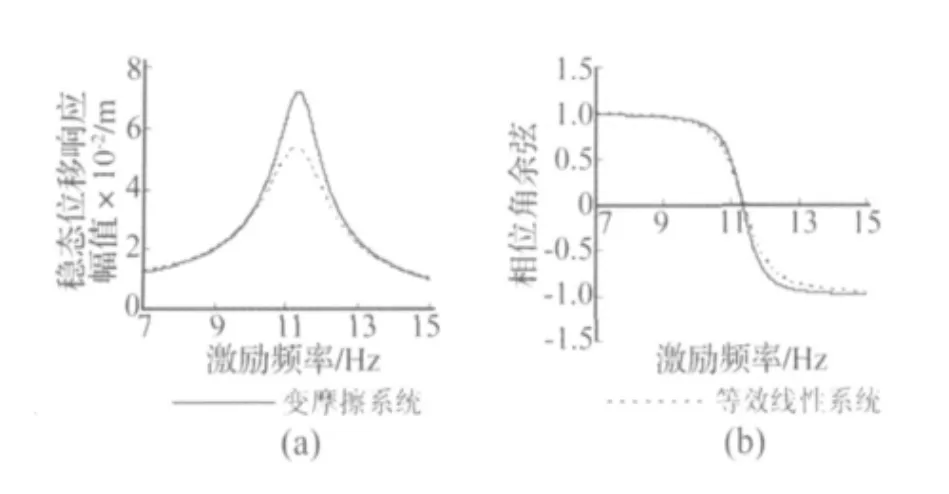
图6 变摩擦系统和等效系统的频率响应特性比较Fig.6 Frequency response characteristic of variable friction system and its equivalent linear system

3 结构－变摩擦TMD系统特性

为了简化非线性项的分析，将TMD相对于主结构的位移y作为未知数，得到主结构和变摩擦TMD在简谐激励下的运动方程:

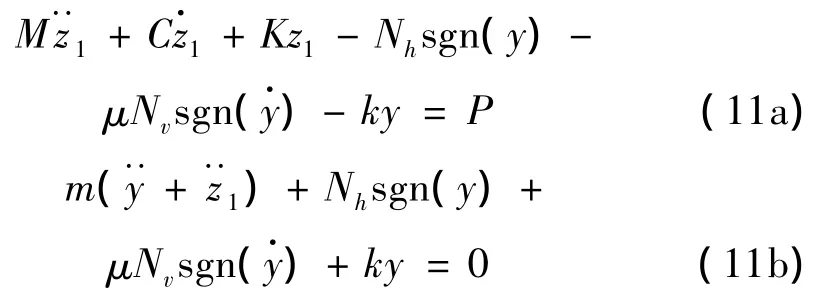
其中，M、C和K分别是主结构的质量、阻尼系数和刚度，m和k分别是TMD的质量和刚度，μ是摩擦面的摩擦系数，z1是主结构相对于地面的位移，y是TMD相对于主结构的位移是摩擦面的正压力tanγ是斜面对正压力Nv的反力的水平分力;N0是弹簧的预压力;γ是斜面倾角，kt是摩擦面上压紧弹簧的刚度系数。

引入参数:r=m/M，ω21=K/M，ω22=k/m，f=ω2/ω1，p(t)=P(t)/M，Nv0=N0/m，Nh0=N0tan(γ/m)，Nhf=kttan2(γ/m)，Nvf=kttan(γ/m)

式(11)变为:

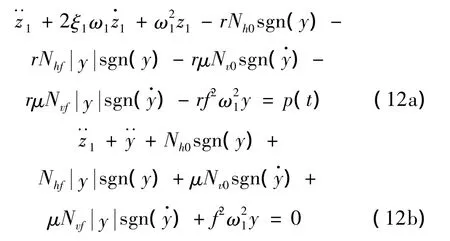
令:

其中φ1是TMD相对于主结构的位移y和主结构相对位移z之间的相位差;φ2是TMD相对于主结构的位移y和激励P之间的相位差。

将式(12)中非线性项展开成傅里叶级数，并取第一项，得下列近似关系:

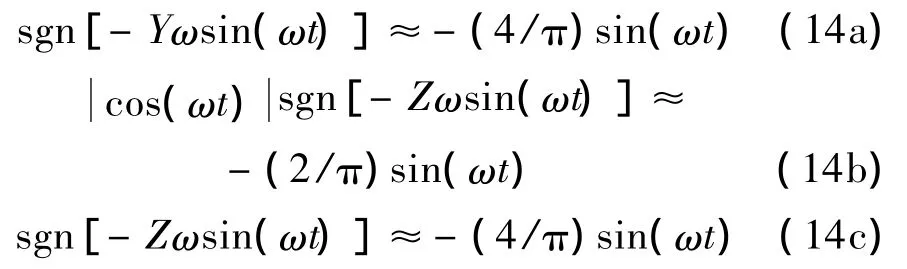
将式(13)和式(14)代入式(12)，通过 cos(ωt)和sin(ωt)两项系数的恒等关系得:

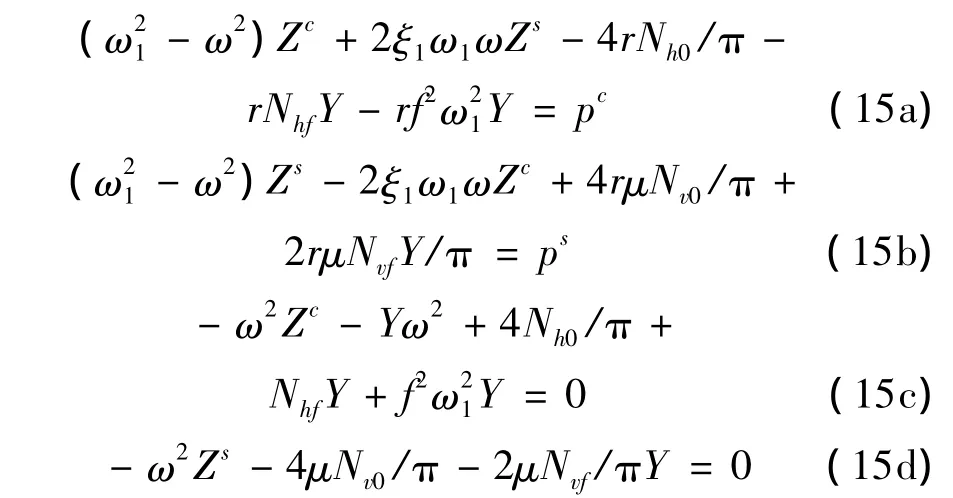
从式(15c)和式(15d)分别将ZcZs用Y表达，并代入式(15a)和式(15b)，消去ZcZs得:

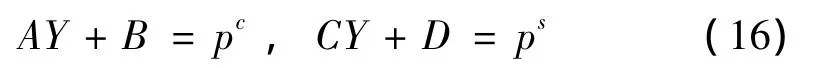
其中，

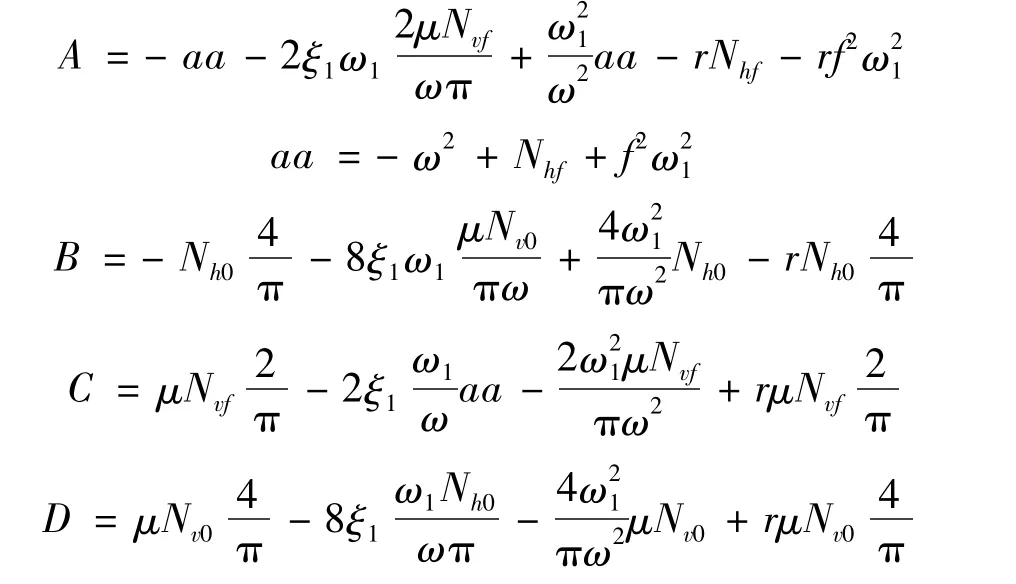
由式(16)，并利用关系(pc)2+(ps)2=P2，解得TMD的运动幅值Y:

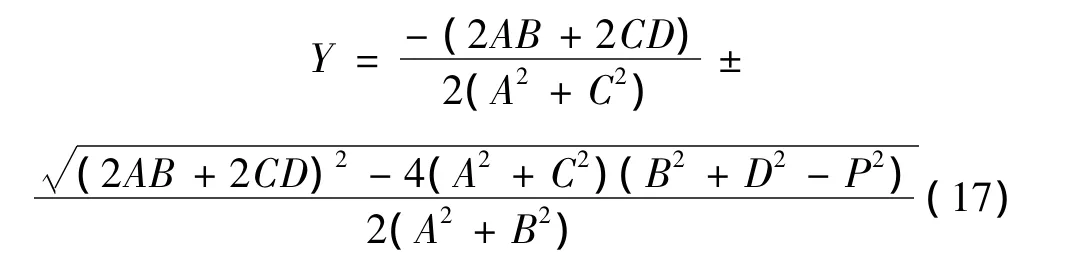
从式(17)可以得到两个Y值，但Y是TMD相对于主结构的位移幅值，只能是大于零的，所以只有正的Y值是有意义的。需要注意的是，式(17)中只有根号下的部分大于等于零，才可以得到正的实数Y。在摩擦力大到一定程度以后，根号下的部分可能出现负值，在这种情况下，就不能用谐波平衡法求系统的响应了，原因就在于谐波平衡法假设系统的响应是简谐的，而当摩擦力相对于主结构的运动比较大时，TMD的运动就会出现静止－运动现象，不再能用简谐运动来描述，所以无法再利用谐波平衡法求解了。

求出Y后，根据式(15)可求出剩下的未知数，从而得到我们关心的一定激励频率和幅值的简谐激励作用下主结构位移幅值。

算例3

主结构:M=430，K=60 300 kN/m，ξ1=0.02;

TMD:m=21.5，k=1 500 kN/m，kt=17 500 kN/m，N0=0摩擦系数 μ=0.1，斜面倾角 γ=15°。根据式(9)和式(10)计算得出等效频率ωe=11.726，等效阻尼比 ξe=0.05

相应的经典阻尼TMD参数为:meff=21.5，keff=

图7给出了无TMD、经典阻尼TMD和变摩擦TMD时主结构稳态位移响应曲线的比较，从图中可以看到，具有变摩擦TMD和经典阻尼TMD，主结构的稳态位移响应曲线有一定的差别，但二者都能有效减小主结构的频响曲线峰值。

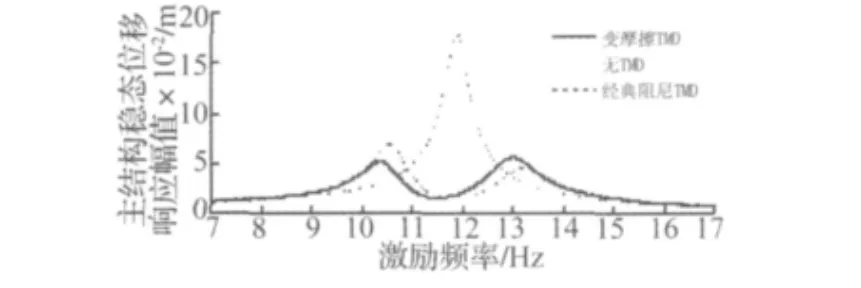
图7 主结构频响曲线的比较Fig.7 Frequency response curve of structure with variable friction TMD，viscous damped TMD and without TMD

4 变摩擦TMD特性的实验研究

4.1 模型设计

本试验着力于原理和性能方面，故采用较为简单的单自由度主结构，如图8，主结构刚度由0.045 m×0.004 m×0.5 m高的钢片提供，主结构的质量由0.6 m×0.7 m×0.01 m钢板，配重块和固定TMD的构件质量组成。本试验主结构质量为75 kg，频率为2.1 Hz。从自由衰减曲线，利用常规的阻尼比计算方法可以得到主结构的阻尼为0.073。

图8 主结构模型和TMD实物图Fig.8 Picture of structure and friction TMD

变正压力式变摩擦TMD构造如图8，TMD质量通过直线轴承安装于滑轨之上，采用滑轨是为了有效减小系统的固有摩擦阻尼;TMD刚度由刚度为100 N/m的拉簧提供，通过增加拉簧的数量来调节TMD的刚度。采用拉簧也是为了进一步减小系统本身的摩擦阻尼，增大阻尼的可调节范围。TMD质量上垂直于滑轨方向TMD运动方向安装另一组导轨，用来安装提供正压力的弹簧，当TMD质量沿滑轨运动时，由于斜面的作用，提供摩擦面正压力的弹簧压缩量随TMD的位移增加而增加，从而使摩擦力随TMD的位移增加而增加。

4.2 简谐激励下变摩擦TMD的特性和控制效果

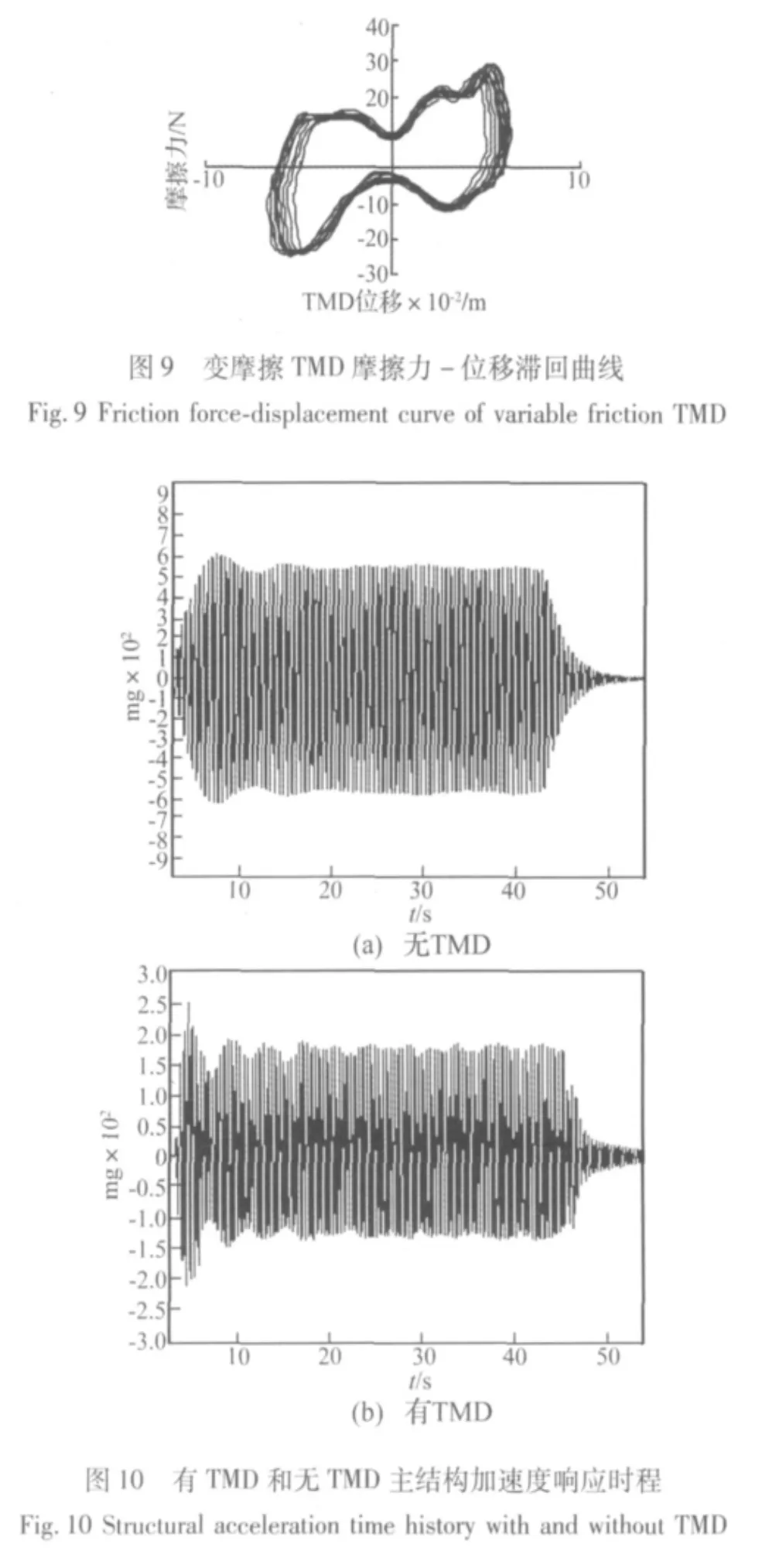
图9给出了变摩擦TMD的摩擦力－位移滞回曲线，可以看出摩擦力随位移增大有增大的现象，基本符合变摩擦TMD理论分析结果。由于本文所进行的只是变摩擦TMD的初步原理试验，模型制作不够精细，试验所得摩擦力－位移滞回曲线并不是严格随TMD位移增大而线性增大，从图9可以看到，滞回曲线在第一象限有轻微的波动。为了获得更为理想的变摩擦效果，需要改进试验模型，这些工作会在后续的研究中逐步开展。图10给出了有TMD和无TMD结构的稳态加速度响应，加上TMD后，结构的加速度由0.55 g变成为0.18 g，体现了变摩擦TMD对简谐激励作用下结构控制的有效性。

5 结论

提出一种变正压力式变摩擦装置，并详细阐述了这种新型变摩擦装置的工作原理。采用一阶谐波平衡法推导了变摩擦系统的等效阻尼比和等效频率，分析了变摩擦系统各参数对其等效阻尼比和等效频率的影响，通过与经典阻尼单自由度系统的比较探讨了单自由度变摩擦系统的频率响应特性。从理论和试验两个方面研究了简谐激励下变摩擦TMD对单自由度主结构振动控制的特点。主要得出以下的结论:

(1)变正压力式变摩擦TMD，有预压力的情况下，运动幅值很小时，等效频率和等效阻尼比随TMD运动幅值增大而减小，当TMD达到一定的运动幅值后，等效频率和等效阻尼比不再随运动幅值的变化而变化。斜面倾角增大，等效阻尼比和等效刚度都增大。倾角越大，增大倾角对阻尼比增大效果越不明显，而对增大频率的效果则比较明显。弹簧预压力只在运动幅值很小时对等效阻尼比和等效频率有一定影响。

(2)变摩擦单自由度系统和相应的等效经典阻尼系统的频率响应特性差别不大，只是峰值有一点差别。设计变摩擦系统的参数时，可以先采用粘滞阻尼的理论进行，再适当考虑阻尼比的折减，设计变摩擦系统的相关参数。

(3)变摩擦TMD－主结构系统和等效经典阻尼TMD－主结构系统的主结构加速度传递函数差别不大，这说明变摩擦TMD系统具有和经典阻尼TMD类似的特性。

(4)变摩擦TMD简谐激励控制效果理论和实验分析表明，变摩擦TMD与经典TMD类似，都能有效减小在简谐激励下主结构的响应。

［1］ 李春祥，刘艳霞，王肇民.质量阻尼器的发展［J］.力学进展，2003，33(2):194－206.

［2］ 韩兵康，杜 冬.结构半主动调谐质量阻尼器的发展［J］.振动与冲击，2005，24(2):46－49.

［3］ Inaudi J A，Kelly J M.Mass damper using friction-dissipating devices［J］. JournalofEngineeringMechanics， 1995，121(1):142－149.

［4］ 田志昌，张黎明.干摩擦在调谐质量阻尼器系统中的应用［J］.工程抗震，2003(1):21－23.

［5］ 钱稼茹，田志昌.滑动屋盖摩擦控制系统的振动台实验研究［J］.地震工程与工程振动，2002，22(2):120－125.

［6］ 闫维明，纪金豹，鄢圣超，等.悬吊式调频质量阻尼器减振控制装置［P］.专利号:ZL 200610057990.8.

［7］ 秦 丽，闫维明，呼学军，等.河南艺术中心标志塔TMD地震控制［J］.北京工业大学学报，2009，35(6):761－768.

［8］ Whiteman W E，Ferri A A.Displacement-dependent dry friction damping of a beam-like structure［J］.Journal of Sound and Vibration，1996，198(3):313－329.