双链式悬索桥地震反应特征研究

丁南宏，林丽霞，钱永久，王常峰

(1.兰州交通大学 土木工程学院，兰州 730070;2.西南交通大学 土木工程学院，成都 610031)

双链式悬索桥指在—个吊杆平面内设有两条主缆的悬索桥，该两条主缆在跨中交叉且互相联结，上下主缆在全跨范围内均匀布置有吊索吊拉桥面加劲梁，如图1所示。双链式悬索桥对恒载和全跨布置的均布活载是由其上下主缆平均负担。当半跨有活载时，荷载将由该半跨的下主缆全部承受，而下主缆此时的形状，恰好符合于承受荷载后主缆的变形，于是悬索桥将不发生S形变形，因而它比单索体系有较大的刚度，其对非对称荷载的适应性较强［1］。可以说双链式悬索桥静力学优点是显著的，但对该类悬索桥动力性能分析的报道非常少。双链式悬索桥的结构特性，决定了其具有独特的动力特性和抗震性能。本文作者曾就双链式悬索桥自振特性进行了研究，并与同跨度同矢高的单链式悬索桥进行了对比分析［2］。目前国内外有许多学者对大跨度悬索桥进行了地震反应的研究［3－6］，但研究对象几乎都为—个吊杆平面内设有一根主缆的悬索桥，而对于双链式悬索桥的抗震性能研究还是一个空白。为保证这种特殊结构形式的抗震安全性，探讨双链式悬索桥抗震性能的特点和规律，寻求合理的抗震结构体系将有着十分重要的工程意义。

图1 双链式悬索桥立面图Fig.1 Double cable suspension bridge profile

双链式悬索桥是钢加劲梁、主缆、吊索和钢筋混凝土主塔两种阻尼特性不同的材料组合体，故不能采用单一阻尼特征参数来表达，需要考虑不同材料的阻尼耗能差异，这会导致主坐标系中的运动方程耦联。不少文献［7－8］采用复振型方法进行分析，取得了满意的结果，但由于复振型方法非常复杂，又没有相应的结构计算软件的配合，工程师很难用此方法进行实际结构分析。文献［9］采用强迫解耦的方法，利用经典阻尼理论对非经典阻尼结构进行分析，研究表明［10］，当结构阻尼比较小时，分析结果具有较好的误差控制，可以为设计采用。基于复阻尼理论求解等效粘滞阻尼比，计算数据与试验数据符合程度较好［11］，说明该方法能够反映不同材料组成的结构的实际情况。

本文以黄河上游某双链柔式钢索悬索桥为工程背景，针对双链式悬索桥独特的结构形式，采用等效粘滞阻尼比近似描述非经典阻尼体系的阻尼耗能。考虑几何非线性及非经典阻尼因素，对桥梁进行地震反应谱和时程反应分析，并就同跨度同矢高的双链式悬索桥和单链式(普通式)悬索桥地震反应进行对比分析，以揭示双链式悬索桥地震反应特征。

1 等效粘滞阻尼比

设组成双链式悬索桥的两种材料钢材和混凝土的阻尼系数分别为 γs和 γc，刚度矩阵分别为［K］s和［K］c;结构质量矩阵为［M］，动力荷载为{P(t)}。根据 Сорокин 复阻尼理论，振动方程为:

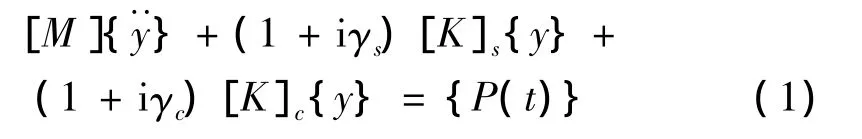
设{y}=［φ］{q}，式中，{y}为节点位移列阵;{q}为模态坐标列阵;［φ］为振型向量组成的矩阵，代入式(1)，并左乘第j振型的振型向量{φ}Tj，由振型正交性得到:

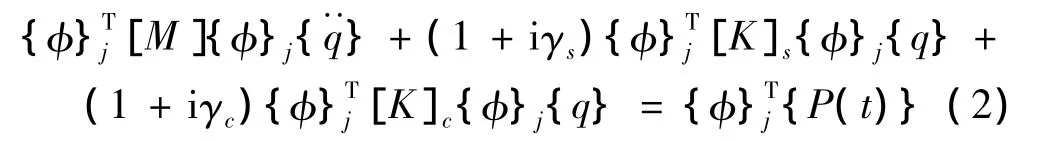
与结构换算阻尼系数为γ的振动方程比较，得到:

设振型中与钢构件相关的振型向量为{φ}js，与混凝土构件相关的振型向量为{φ}jc，由式(3)得到换算阻尼系数:

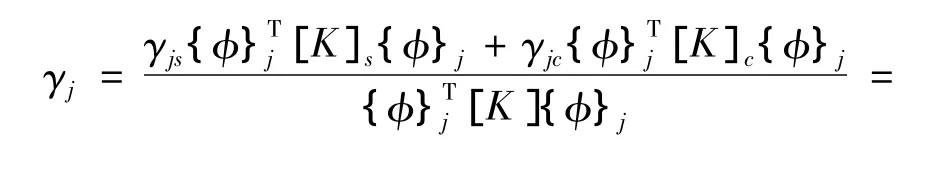
则等效粘滞阻尼比:

2 双链式悬索桥地震反应谱分析

2.1 双链悬索桥有限元模型及自振特性

青城桥距黄河大峡水库下游3 km处，结构形式为单跨180 m的双链柔式钢索悬索桥，边跨为4 m×16 m简支梁，如图1所示。具体结构参数见文献［2］。

建立空间有限元模型:① 采用全桥脊梁模式，主缆和吊索采用只受拉三维杆单元［2］;主跨加劲梁采用空间梁单元和刚臂单元模拟;主塔采用空间梁单元。② 对于主缆和吊索等柔性构件，计入轴向拉力对刚度的贡献，即用几何刚度矩阵考虑恒载索力的线性二阶影响。③ 边界条件为塔底在地面固结，锚碇与地基固结。

对于非线性效应突出的悬索结构，在动力分析之前须进行恒载起点的非线性静力分析，以计入恒载起点的P－Δ效应及几何非线性效应的影响。采用Newton－Raphson迭代求解，确定结构在自重下的切线刚度矩阵，然后在此基础上进行动力特性分析。双链式悬索桥具有普通悬索桥振型分组显著的特性，结构以主梁振动为主的振型最先出现，而后是索的振动和梁的高阶振型，以塔为主的振动在较后面，这与单链悬索桥模态趋势基本一致［2］。单链悬索桥竖向第一振型一般为反对称竖弯，而双链悬索桥竖向第一振型为正对称竖弯，在相同结构参数情况下，双链悬索桥能有效提高桥梁一阶竖弯振动频率。

2.2 反应谱分析

反应谱振型分解法的振型组合方式及应组合的振型数对大跨悬索桥地震反应的影响十分显著。依据文献［12－13］建议，本桥反应谱振型分解法使用CQC组合，组合振型时使用前400阶振型，此时在X、Y、Z各方向的振型参与质量分别为95.8%、93.4%和92.1%，超过我国《公路桥梁抗震设计细则》(JTG/T B02－01－2008)所规定的90%。由该桥自振特性［2］分析知，其第一阶自振周期是3.759 6 s，我国《公路桥梁抗震设计细则》(JTG/T B02－01－2008)中给出了0 s～10 s周期的反应谱，因最大周期落在此区间内，勿需对规范反应谱进行修正。场地类别为Ⅱ类场地土;设防烈度为7度。设青城桥的加劲梁、主缆和吊杆阻尼比 ξs=0.02，混凝土主塔阻尼比 ξc=0.05。沿桥纵向、横向和竖向3个方向的地震反应分别见表1～表3。表1～表3 中，Δx，Δy，Δz分别为纵向、横向和竖向位移;FN，Fsz，My分别为轴力、面内剪力和面内弯矩，T，Fsy，Mz分别为扭矩、面外剪力和面外弯矩。

表1 双链式悬索桥纵向地震反应Tab.1 Longitudinal seismic response of bridge

纵向地震激励下，双链式与单链式悬索桥索力接近，前者比后者索力(上下链索力和)略大;双链式比单链式悬索桥加劲梁、主塔内力略小;加劲梁位移二者接近。

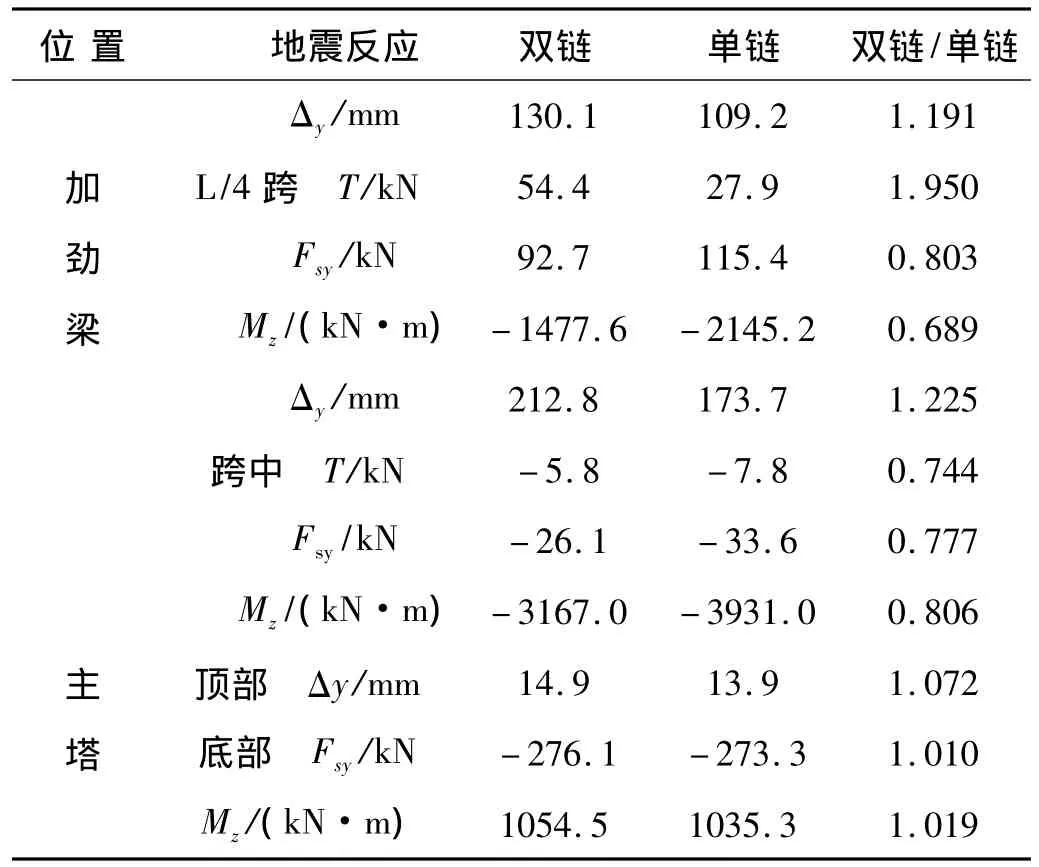
表2 双链式悬索桥横向地震反应Tab.2 Transverse seismic response of bridge

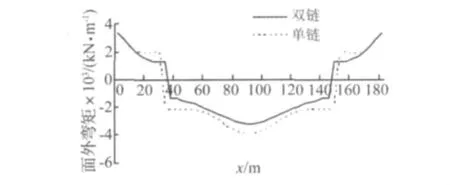
图2 加劲梁面外弯矩MzFig.2 Out-of-plane moment Mzof stiffening girder

横向地震激励下，双链式比单链式悬索桥边跨索力小，中跨索力(上下链索力和)大;除加劲梁扭矩T外，双链式悬索桥面外剪力Fsy、面外弯矩Mz比单链式悬索桥小，加劲梁面外弯矩Mz如图2所示;双链式悬索桥加劲梁横向位移比单链式悬索桥大。

表3 双链式悬索桥竖向地震反应Tab.3 Vertical seismic response of bridge

竖向地震激励下，双链式悬索桥索力比单链式悬索桥小;加劲梁轴力接近，但面内剪力Fsz、面内弯矩My相差较大;加劲梁竖向位移Δz最大值接近，但分布规律相差很大，双链式比单链式悬索桥L/4跨竖向位移小，而跨中竖向位移大，如图3所示;双链式悬索桥塔顶纵向位移Δx比单链式悬索桥小。

图3 加劲梁竖向位移ΔzFig.3 Vertical displacement Δzof stiffening girder

3 非线性地震时程反应分析

时程分析采用时域内逐步积分的Wilson－θ法，计算步长取0.02 s。时程积分时的地震记录的持续时间对大跨悬索桥地震反应的影响十分显著。依据文献［13］建议:用时程积分法时，地震波的持续时间应尽可能长，一般可取60 s左右;竖向地震必须考虑，竖向地震加速度取相应的水平向加速度的2/3。另外，从历次强震记录中选取了El-Centro波作为地震动输入，记录烈度为7度，较好地符合了该桥的设防地震要求。

加劲梁位移最大值如图4所示，双链式悬索桥加劲梁横向位移比单链式悬索桥大;竖向位移最大值差别很大，单链式悬索桥竖向位移最大值出现在L/4跨附近，双链式悬索桥位移分布比较均匀，最大位移出现在L/2跨附近，其L/4跨位移减小到单链式的40%。

图4 加劲梁位移Fig.4 Displacement of stiffening girder

加劲梁L/4跨位移时程曲线如图5～图6所示。双链式悬索桥加劲梁横向位移各时点计算值总体上大于单链式悬索桥计算结果，而竖向位移各时点计算值总体上小于单链式悬索桥计算结果。

4 单、双链悬索桥地震反应对比分析

令双链悬索桥实桥的上、下链竖向坐标分别为y02、y01，同跨度同矢高具有任意主缆形状的双链式悬索桥的上、下链竖向坐标分别为 y2、y1，定义主缆形状系数［14］:

表4 纵向地震下结构地震反应Tab.4 Longitudinal seismic response of bridge

则α=0时为双链式悬索桥实桥，α=0.5时为单链式悬索桥，即可将单链式悬索桥作为双链式悬索桥同一索面两主缆合并的特殊情况。在双索悬索桥实桥有限元模型基础上，保持跨度、矢高、材性等结构参数不变，但在—个吊杆平面内只设一条主缆，且主缆截面面积取为双索悬索桥的两条主缆截面面积之和，即得单索悬索桥有限元模型。取主缆形状α分别等于0，0.1，0.3，0.5的各双链式悬索桥，对比分析各种双链式悬索桥地震反应。加劲梁最大位移、主缆最大索力、塔梁最大内力分别见表4～表6，字母含义同表1～表3。

纵向地震下，随双链位置接近，加劲梁L/4、L/2截面竖向位移Δz略有增大;边跨索力和中跨索力FN(双链式为上下链索力之和)减小，如双链式比单链式实桥两类索力分别大5%和6%。在竖向、纵向地震作用下，不同主缆形状对悬索桥塔底内力变化影响很小，除加劲梁L/4、L/2截面面内剪力、弯矩My有显著差别外，其他内力接近;随双链位置接近，L/4截面面内剪力增大，L/2截面面内剪力减小，面内弯矩My先增加后减小。加劲梁面内弯矩My随主缆形状系数α变化规律非单调，如α=0.4时，加劲梁内力较小，可作为设计选型的动力学依据。

表5 横向地震下结构地震反应Tab.5 Transverse seismic response of bridge

横向地震下，单、双链式悬索桥加劲梁横向位移Δy之间有显著差别，如双链式实桥比单链式悬索桥加劲梁L/4、L/2截面横向位移Δy分别大17%和13%，而双链式之间差别很小。单、双链式悬索桥主缆索力FN之间有显著差别，如双链式实桥比单链式悬索桥两类索力分别小98%和51%，而双链式之间差别很小，说明双链式较为安全。不同主缆形状对塔底内力影响较大，双链式比单链式塔底内力小，如双链式实桥比单链式悬索桥塔底轴力 FN、剪力 Fsy和弯矩 Mz分别小211%、78%和38%，而双链式间除轴力差别较大外，其余内力差别不大，说明双链式可大幅度提高桥塔横桥向抗震性能。不同主缆形状对加劲梁L/4截面面内外剪力、弯矩有显著影响，其它内力接近;单双链式之间内力有显著差别，双链式之间差别在4%以内;双链式悬索桥加劲梁面外剪力Fsy、弯矩Mz比单链式悬索桥的小，说明双链式悬索桥加劲梁横向抗震性能优于单链式悬索桥。

表6 竖向地震下结构地震反应Tab.6 Vertical seismic response of bridge

竖向地震下，随双链位置接近，加劲梁L/4截面竖向位移Δz先增大后减小，而L/2截面竖向位移Δz先减小后增大;双链式实桥加劲梁L/4截面竖向位移小于单链式悬索桥，而其L/2截面竖向位移大于单链式，双链改善了单链式桥L/4截面竖向位移普遍偏大的现象;α=0.2时，双链式与单链式位移接近，可作为动力选型的依据。索力FN变化复杂，如双链式实桥比单链式悬索桥边跨索力和中跨索力分别大15%和18%，但α=0.4时，双链式甚至比单链式悬索桥索力还小，可作为动力学选型的依据。

5 结论

(1)纵向地震下，不同主缆形状对加劲梁位移、塔底内力变化影响很小。双链式与单链式悬索桥索力接近，前者比后者索力略大;双链式悬索桥加劲梁内力、竖向位移、主塔内力比单链式悬索桥略小。

(2)竖向地震下，不同主缆形状对地震反应影响较为复杂，为桥梁结构设计选型提供了动力学依据。双链式悬索桥加劲梁L/4截面竖向位移小于单链式悬索桥;而其L/2截面竖向位移大于单链式悬索桥，双链改善了单链式悬索桥L/4截面竖向位移普遍偏大的现象。

(3)横向地震下，各种不同主缆形状的双链式悬索桥地震反应变化较小，但双链式与单链式悬索桥之间差别较大。双链式悬索桥比单链式悬索桥边跨索力小，而中跨索力大，加劲梁横向位移大，但双链式悬索桥比单链式悬索桥的加劲梁位移、主缆索力、塔底内力、加劲梁面外剪力和弯矩都小，说明双链式悬索桥横向抗震性能优于单链式悬索桥。

［1］ 严国敏.现代悬索桥［M］.北京:人民交通出版社，2002.

［2］ 林丽霞，吴亚平，丁南宏.双索悬索桥结构参数对自振特性的影响分析［J］.铁道学报，2007，29(4):91－95.

［3］ Huang M H，Thambiratnam D P，Perera N J.Vibration characteristics of shallow suspension bridge with pre-tensioned cables［J］.Engineering Structures，2005，27(13):1220－1233.

［4］ 李志岭，秦 权.用R1tZ法分析江阴悬索桥地震反应的影响［J］.工程力学，2003，20(1):32－36.

［5］ Arzoumanidis S，Shama Y，Ostadan A.Performance-based seismic analysis and design of suspension bridges［J］.Earthquake Engng Struct Dyn，2005，34(1):349－317.

［6］ 秦 权，楼 磊.非经典阻尼对悬索桥地震反应的影响［J］.土木工程学报，1999，32(3):18－22.

［7］ 王建有，陈健云.基于复模态的非比例阻尼结构参数识别研究［J］.哈尔滨工业大学学报，2005，37(12):1647－1649.

［8］ 周锡元，董 娣，苏幼坡.非正交阻尼线性振动系统的复振型地震反应叠加分析方法［J］.土木工程学报，2003，36(5):31－36.

［9］ 俞瑞芳，周锡元.非比例阻尼弹性结构地震反应强迫解耦方法的背景和数值检验［J］.工业建筑，2005，35(2):52－56.

［10］ 桂国庆，何玉敖.非比例阻尼结构体系近似解耦分析中的误差分析［J］.工程力学，1994(4):40－50.

［11］ 龚炳年，郝锐坤，赵 宁.钢－混凝土混合结构模型动力特性的试验研究［J］.建筑结构学报，1995，16(3):37－43.

［12］ 邓育林，贾贤盛.大跨度悬索桥地震反应中高阶振型的影响分析［J］.工程抗震与加固改造，2008，30(2):24－24，81.

［13］ 秦 权，罗 颖，孙 浩.悬索桥上部结构的抗震设计［J］.清华大学学报(自然科学版)，1998，38(12):52－56.

［14］ 丁南宏，钱永久，林丽霞，等.双链式悬索桥在单车荷载下的振动特征［J］.振动与冲击，2010，29(7):216－220.