随机最优控制下矩形薄板受面内随机参数激励的首次穿越研究

葛 根，王洪礼，许 佳

(1.天津工业大学 机械学院，天津 300160;2.天津大学 机械学院工程力学系，天津 300072)

近来越来越多的学者对各种边界条件的矩形薄板的非线性振动特性进行了大量的研究［1－5］，发现了丰富的非线性动力学现象，如分岔，混沌等。这些文献一般都是使用确定性非线性系统理论进行研究的，而事实上，薄板在实际情况中往往受到随机激励的作用。葛根等［6－7］研究了矩形薄板在摩擦边界和四边简支边界在面内高斯白噪声激励时，一阶模态和二阶模态的随机稳定性和随机Hopf分岔和问题。但是对矩形薄板在随机激励下的可靠性问题(即系统能量首次穿越安全域边界问题)，及对如何对系统施加反馈控制来增加系统安全性的策略问题都尚未研究。

本文在文献［6－7］基础上建立了四边简支的矩形薄板在受面内含高斯白噪声信号激励下时，受控制力作用的二阶随机参数激励模型，并用拟不可积Hamilton系统随机平均法把受控薄板振动系统广义能量表示为一维Itǒ扩散过程。随后根据随机动态规划方法，得到了系统的最优反馈控制策略，并进一步得到了受控系统的条件可靠性函数满足BK(Backward Kolmogorov)方程，设定边界条件和初值及终值条件后，用蒙特卡罗数值模拟验证了理论分析。

1 受控薄板随机振动模型的建立

图1 矩形薄板振动模型及坐标Fig.1 The model of a rectangular thin plate and the coordinate system

如图1所示薄板，矩形薄板长宽分别为a和b，厚度为h，在x=0，x=a，y=0，y=b四边简支。在板中面建立如图1所示的坐标，设 u，v，w 分别为 x，y，z方向的位移。在x=0，x=a两边受面内激励p(t)，为绝对刚硬梁传来的板中面内的分布载荷，其形式为:p(t)=p0+p'ζ(t)，其中，p0为均布载荷，ζ(t)为 0 均值，强度为2D的高斯白噪声，p'为噪声的幅值。G(x，y)为外加控制力，形式满足:

该薄板可认为是柔性大挠度板，参考文献［2］可建立板的横向振动方程为:

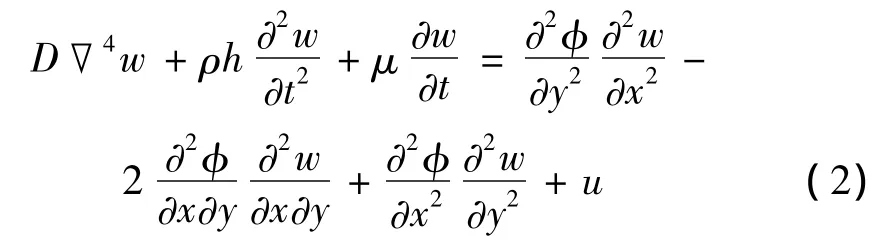
板的简支边的位移边界条件可表示为:

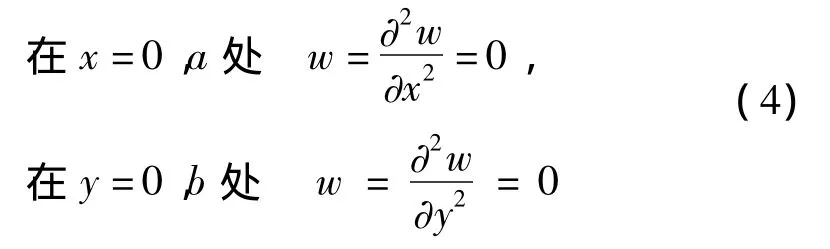
满足位移边界条件式(4)的板的二阶模态为:

根据Galerkin变分法，可求得离散后薄板的常微分形式的运动方程:

其中参数变化形式为:

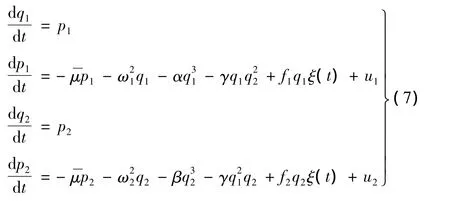
为研究系统(7)在随机激励下系统能量的变化，设系统的Hamilton函数(广义能量)为:

其中:

系统(7)可写为Itô方程:

其中:B(t)是标准Weiner过程。

“◦”表示Itô意义下乘积。

该Hamilton系统不存在与H(t)独立对合的首次积分，该系统为一个拟不可积Hamilton系统。根据拟不可积Hamilton系统的定义及性质，可知系统式(7)依概率收敛到一维Itô扩散过程:

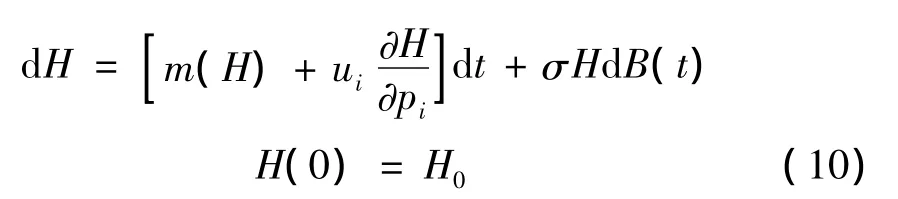
其中，m(H)和σ(H)分别是未受控系统的Itô随机过程的漂移系数与扩散系数。

使用拟不可积 Hamilton系统的随机平均法［8］，得到:

这里R是方程(17)的根。

2 系统的随机最优控制

系统的最优控制一般是指通过反馈控制使原来不稳定的随机动力学系统变得稳定，或以此来提高系统的稳定度。在半无限长时间上的随机稳定化是一种具有待定成本函数的遍历控制方法。最优控制的目标常用一个泛函的极小或极大来表示，该泛函称为成本泛函或性能指标。对随机最优控制，受控系统的状态与控制皆为随机过程，该泛函为随机变量，因此性能指标取为该泛函的数学期望。

随机动态规划方法就是对给定的随机最优控制问题，建立并求解随机动态规划方程，确定最优控制，然后求解最优状态。可定义值函数:

U为控制力受到的约束，“sup”是“supremum”的缩写，T为终止时间。值函数V(t，H)就是使随机受控系统的条件可靠性函数取最大。根据动态规划原理［9－10］，可导出V(t，H)所满足的随机动态规划方程:

方程(19)的边界条件为:

方程(19)的终值条件为:

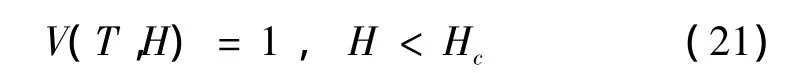
式(19)～式(21)组成了受反馈控制的拟不可积Hamilton系统的可靠性问题，构成了一个以最大可靠性为目标的非线性随机最优控制策略。以拟Hamilton系统的随机平均法及随机动态规划原理为基础，从而可求出最优控制形式。

假设控制力有界，满足－ bi≤ui≤bi，(i=1，2)。则方程(19)中的 ui(∂H/∂pi)(∂V/∂H)在时取最大且每项为正。所以，最优控制力可以写为:

由于值函数V(t，H)都是H的递减函数，即:∂V/∂H ＜0，因此，式(22)可简化为:

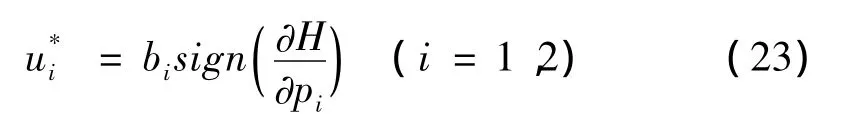
其中:

考虑当H→0时，忽略高阶小量可得:

3 系统首次穿越分析

随机振动系统的可靠性可用许多指标来度量，包括可靠性函数、首次穿越损坏的概率密度函数和首次穿越时间的均值等。其中可靠性函数定义为系统在时间区间［0，t］内无损坏地工作的概率［11］。

图2 系统能量安全域示意图Fig.2 Safe domain of H

假设系统在状态空间中的安全域为一开域 Ω =［0，Γ )，其中Γ是Ω的平滑边界。引入可靠性函数}其中P表示条件概率。

得到受控系统的可靠性函数满足的BK(Backward Kolmogorov)方程

方程(11)的初始条件为:

方程(11)的边界条件为:

Γe为系统广义能量的安全界限值。

首次穿越的条件概率为:

假设系统首次穿越安全域边界的时间为T，则首次穿越时间T满足的条件概率密度为:

对于边界是奇异边界的 Hamilton系统来说，式(31)的边界条件由扩散系数α，漂移系数β和特征标值c来决定，由参考文献［7］可知 H=0在特征标值cl＜1时为吸引自然边界。

则对于左边界H=0为进入边界来说，对应的BK方程的边界条件为:

由于可靠性函数、首次穿越损坏的概率密度函数所满足的方程均为偏微分方程，一般情况下无法得到精确解，只能求得数值解，这里我们采用有限差分法来求得方程的数值解。

4 数值结果

首先我们研究随机激励噪声强度对未受控系统的条件可靠性函数和首次穿越概率密度函数的影响。取=0.5，ω22=0.5，f1=0.5，f2=1.35。安全域边界 Hc=1。用(—…－·－)表示分析结果;用(■●★)表示数值结果。

我们从图3可以看出:当随机激励强度D从0.5增加到0.8时，系统状态的可靠性函数下降会随着噪声加强变得越来越快。此现象说明了随机噪声的强度对此时系统可靠性函数的影响，从图4可以看出，首次穿越时间概率密度的峰值会随着噪声强度的增大而升高，对应的峰值时间也会提前。

为研究结构参数中比较有代表性的刚度系数ω21，ω22变化对系统可靠性的影响。取噪声强度D=0.5，其他参数保持不变。图5显示了当刚度系数从0.5上升到1.0时，系统的可靠性函数随时间下降明显变慢。说明增加矩形薄板的刚度对保障振动安全有显著作用。

然后，我们研究系统在受控情况下系统的首次穿越情况随着控制力幅值变化的情况。

图6 系统可靠性函数随控制力幅值变化图Fig.6 Reliability function of system(24)

图6显示出随着控制力幅值的变化，从b1=0(表示未受控系统)上升到b1=0.2和b1=0.8时，系统的可靠性函数随时间的降低变得缓慢，这说明对系统施加反馈控制是增加系统安全性的有效措施。

以上的分析表明:随机系统在稳定性条件被破坏后与确定性系统一样都会发生损坏，而随机系统的非线性动力学行为与确定性系统的动力学现象有所不同。随机系统由于受到随机因素的作用，当满足一定的条件时，系统发生破坏是以一定的可能性(概率形式)来反映的。这说明即使满足一定的条件，系统也并不是一定会发生系统能量超越安全域边界的情况，发生的概率反映了发生损坏的可能性的大小，可见随机系统的复杂性。同时，可以发现当系统参数发生变化时，系统发生破坏的概率也会发生相应的变化，我们可以根据实际的需要，通过调节系统自身参数，或者对系统加以反馈控制，从而降低产生首次穿越的概率，加强系统的可靠性。

5 结论

本文的主要工作为:

(1)首先建立了四边简支矩形薄板的受面内随机激励的受控随机动力学模型;

(2)拟不可积Hamilton系统随机平均法被用于将系统能量(Hamilton函数)的变化过程简化为一个一维扩散过程。随后以使受控系统的可靠性最大为目标函数得到了随机反馈控制策略;

(3)最后以受控可靠性函数满足的BK方程和首次穿越条件概率密度方程的数值模拟得出噪声强度、系统刚度系数对系统可靠性的影响，从而验证了控制策略的有效性。

［1］ Zhang W， LiuZ M， YuP. Globaldynamicsofa parametrically and externally excited thin plate.［J］.Nonlinear Dynamics，2001，24:245－268.

［2］ Zhang W.Global and chaotic dynamics for a parametrically excited thin plate.［J］.Journal of Sound and vibration，2001，239(5):1013－1036

［3］ 杨志安，赵雪娟.非线性弹性地基上矩形薄板受双频参数激励作用的非线性振动［J］.应用力学学报，2007，24(3):494－498.

［4］ 杨志安，赵雪娟，席晓燕.非线性弹性地基上矩形薄板的非线性振动与奇异性分析［J］.振动与冲击，2006，25(5):69－73.

［5］ 杨志安，赵雪娟，席晓燕.非线性弹性地基上矩形薄板的主参数共振［J］.岩土力学，2005，26(12):1921－1925.

［6］ 葛 根，王洪礼，许 佳.矩形薄板在面内随机参数激励下的随机稳定性与分岔研究［J］.振动与冲击，2009，28(9):91－94，194.

［7］ 葛 根，王洪礼，许 佳.矩形薄板在面内随机参数激励下的随机分岔研究［J］.振动与冲击，2011，30(9):253－258.

［8］ Zhu W Q，Yang Y Q.Stochastic averaging of quasinonintegrable－hamiltonian systems［J］.Journal of Applied Mechanics，1997，64(1):975－984.

［9］ Zhu W Q，Ying Z G，Soong T T.An optimal nonlinear stochastic control strategy for randomly excited structural systems［J］.Nonlinear Dynamics，2001，24:31－ 51.

［10］ Zhu W Q. Nonlinear stochastic dynamics and control:framework of Hamiltonian theory［M］.Beijing:Science Press;2003.

［11］ Gan C B， Zhu W Q. First passage failure of quasinonintegrable－Hamiltonian Systems［J］.ASME Journal of Non－Linear Mechanics，2001，36:209－220.