高速列车作用下简支梁车桥耦合振动随机响应分析

李小珍，朱 艳，强士中

(西南交通大学 土木学院，成都 610031)

车辆－桥梁耦合分析始于19世纪40年代，至今已有150多年的历史了。从最初的移动荷载分析模型到轮轨密贴模型再到现在的允许轮轨分离即车辆－线路－桥梁模型，所得到车辆和桥梁的响应只是一个或者多个样本值，车桥耦合运动实质上是一个随机过程，由于涉及多学科的交叉，加之随机振动理论建立至今只有60多年的历史，因此运用随机理论对耦合系统进行的研究十分有限。从上世纪60年代起，各国的学者开始使用移动随机荷载模型进行车桥耦合随机振动分析［1］，至今该模型仍被许多学者采用［2～3］，但是移动荷载分析模型无法考虑车辆的随机性以及车辆桥梁的相互作用。目前，Monte-Carlo法、协方差分析法、演变随机响应法以及虚拟激励法等均被应用到车桥系统的随机分析中［4～7］。其中虚拟激励法由于其精确、高效的优势，被应用于抗风、抗震、车桥耦合等多个方面［8～11］。对于平稳激励问题，虚拟激励法可将随机响应转化为稳态简谐响应分析，对于演变非平稳随机激励问题，虚拟激励法可将其响应分析转化为瞬态时程分析。

本文采用虚拟激励法对空间车桥耦合系统的随机性进行分析，以三跨简支梁为例，讨论桥梁、车辆在不同车速下随机响应的变化规律。

1 车桥系统非平稳随机响应

1.1 系统响应的均值

车辆－桥梁空间耦合系统运动方程可写成:

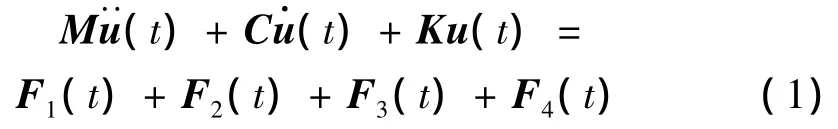
式中，M，C，K分别为系统的质量、阻尼和刚度矩阵

F1(t)为车辆重力引起的确定性荷载项

Fi(t)(i=2～4)为由轨道高低、方向和左右轨高差不平顺引起的随机荷载项

运动方程(1)的解用杜哈米积分表示为:

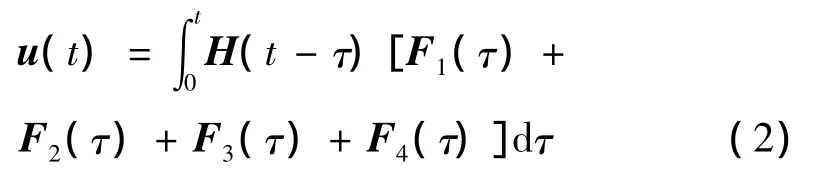
耦合系统响应的均值为:

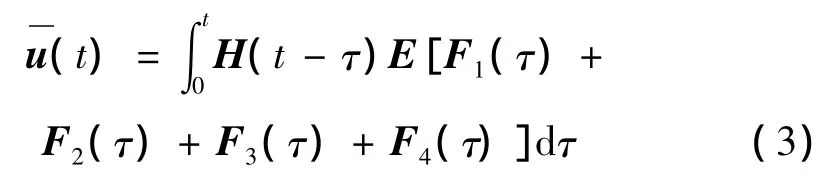
假设轨道不平顺为零均值平稳过程，式(3)可化为:

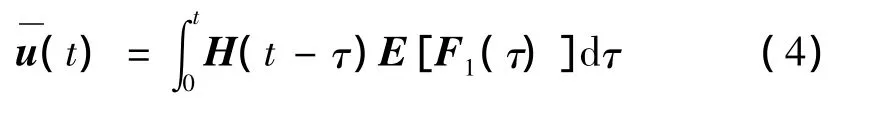
由式(4)可知，系统响应的均值是由确定性荷载项引起的。

1.2 构造车桥系统的虚拟荷载

响应的方差矩阵［12］为:

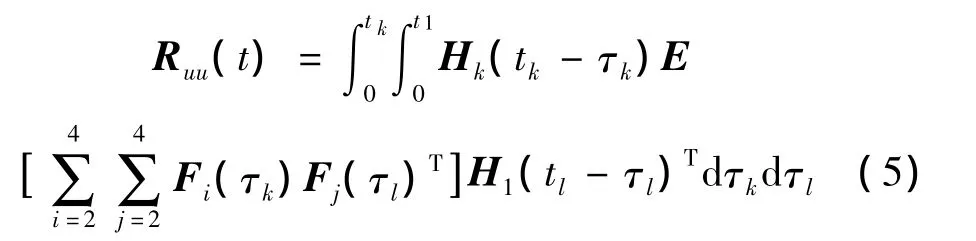
假设随机荷载项表示为:

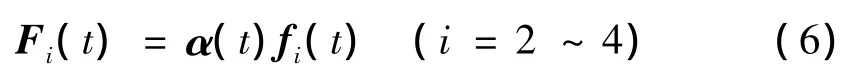
式中α(t)为表示轮对位置的矩阵，fi=［fi1(t)fi2(t)… fin(t)］T是由轮轨接触点处轨道方向不平顺(i=2)、高低不平顺(i=3)和左右轨高差不平顺(i=4)组成的向量，具体表达式可以写成:

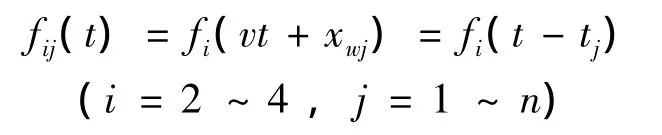
其中，xwi为第i个轮对的局部位置;v为车辆的行驶速度;t为车辆的行驶时间;ti为第i个轮对的行驶时间间隔，得到响应的方差矩阵为:

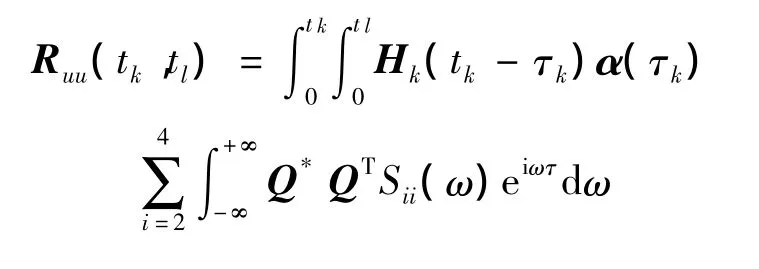
式中:

I(ω，t)=∫0tH(t－ τ)α(τ)Qeiωτdτ，I(ω，t)可看作由激励 α(τ)Qeiωτ引起的响应，因此构造虚拟激励:

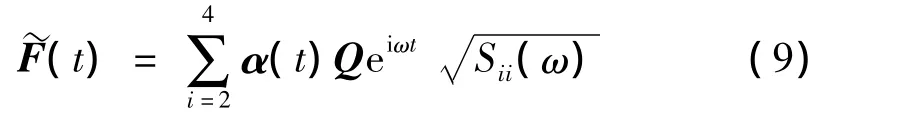
由虚拟激励得到的响应为:

式(7)和式(11)相吻合，从而证明了虚拟激励构造的正确性。

2 车桥耦合系统计算模型

2.1 模型的建立

将车辆和桥梁看成两个子系统，分别建立车辆和桥梁系统的模型。

车辆系统空间模型，独立自由度总数为15，分别为车体和前后两个转向架的横摆、浮沉、侧滚、点头和摇头［13］，即:

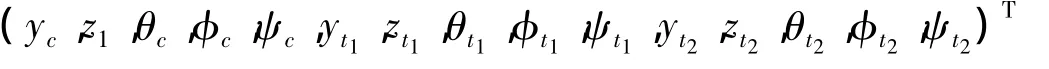
其中下标c代表车体，t1和t2代表前后两个转向架。w1～w4分别代表4个轮对。lc为车辆定距之半，lt为车辆轴距之半。

车辆系统运动方程可写成矩阵的形式:

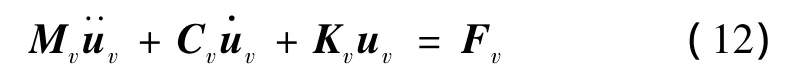
式中:Mv，Cv，kv分别为车辆系统的质量、阻尼和刚度矩阵，Fv为车辆系统受到的车桥系统相互作用力。

桥梁系统模型采用空间梁单元形式，每个单元节点有6个自由度，分别为沿着x，y，z轴的平移和绕着x，y，z轴的转动。桥梁系统的运动方程可写成矩阵的形式:

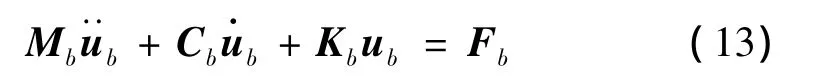
式中，Mb，Cb，Kb分别为桥梁系统的质量、阻尼和刚度矩阵。Fb为桥梁系统受到的车桥系统相互作用力。ub=(xb，yb，zb，θxb，θyb，θzb)T。

2.2 车桥系统运动方程的求解

采用分离迭代法［14］求解系统运动方程。将车辆和桥梁看成两个相对独立的子系统，分别建立二者的运动方程，如式(12)和(13)所示，并通过位移协调条件和力的平衡条件将两个子系统联系起来，通过迭代过程来满足协调条件与平衡关系。对子系统的分离求解采用Newmark－β直接积分法。

3 虚拟激励法的验证

本节以德国ICE3动车通过单跨32 m简支梁(墩高15 m)为例，检验虚拟激励法的正确性。32 m简支梁弹性模量E=3×1010N/m2，泊松比为0.2，密度为ρ =3.64 ×103kg/m3，刚度为 Ixx=35.4 m4，Iyy=9 m4，Izz=70.158 m4，面积为 7.5 m2。阻尼比为 0.02，车辆速度为220 km/h，轨道不平顺的波长范围为1～80 m，计算频率的范围为0.3～60 Hz，频率增量为0.3 Hz。采用德国低干扰谱［15］。将使用本文提出的方法得到的计算结果与使用Monte Carlo法计算得到的结果进行对比，在Monte Carlo法中，采用三角级数法模拟轨道不平顺的样本。

采用Monte Carlo法计算时，分别选取500、5 000、10 000和20 000个样本进行比较。图1～图4为桥梁响应的均值和标准差比较，图5、图6为车体加速度的均值和标准差比较，图7、图8为动车首轮对受到的轮轨力的均值和标准差比较。

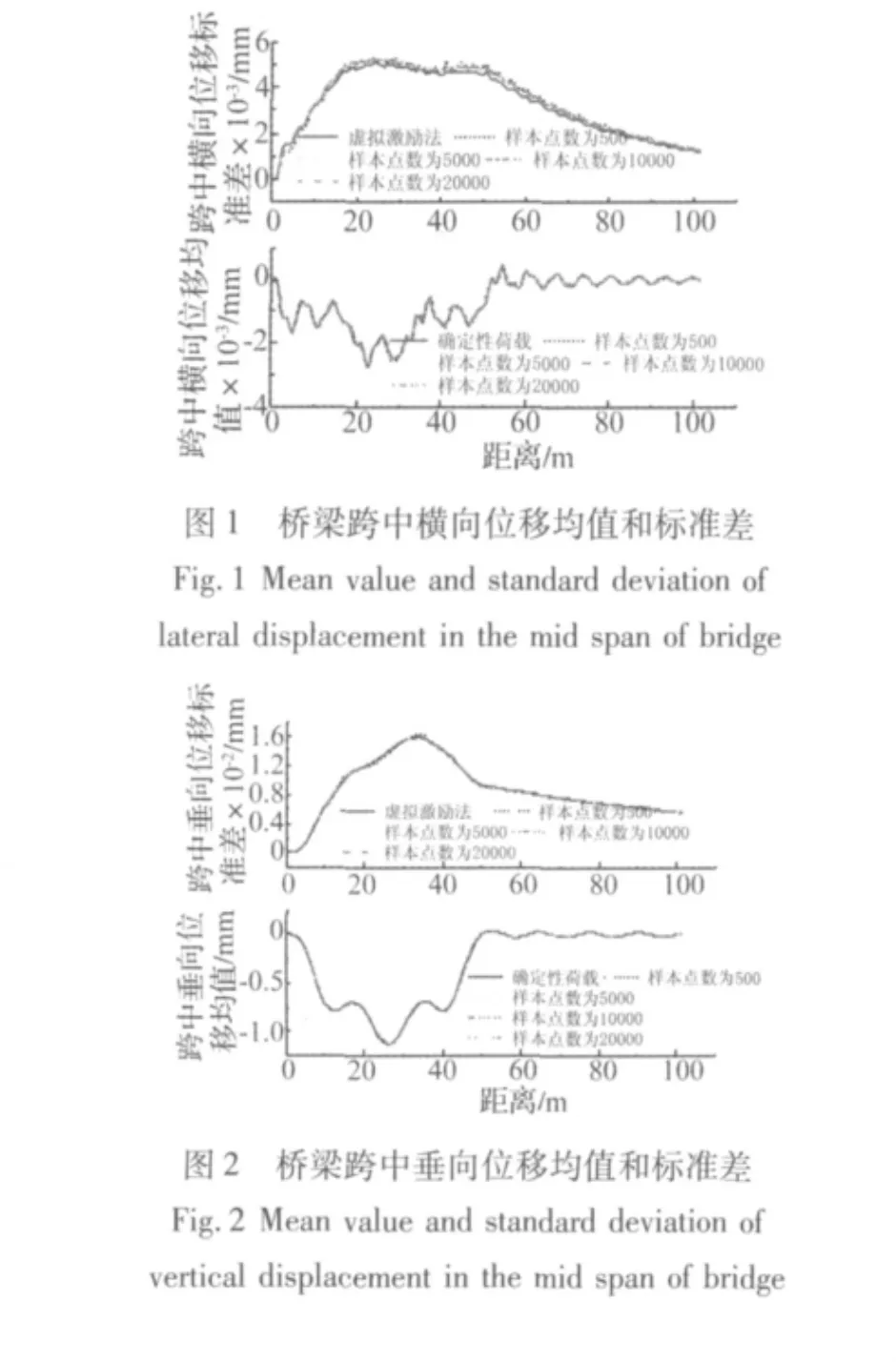
由图1和图2比较可以看到，桥梁横向位移的标准差除以相同时刻下均值的比值均比桥梁垂向位移的标准差除以相同时刻下均值的比值大，说明跨中横向位移的随机性较其垂向位移的随机性要大。

同理，由图3和图4比较可以发现桥梁跨中横向加速度的随机性较其垂向加速度的随机性要大。

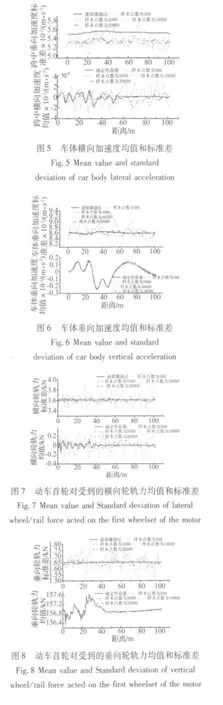
由图5和图6可以看到，车体加速度的标准差比其均值要大，说明车体加速度的随机性比较大。

由图7和图8可以看到，动车首轮对受到的横向轮轨力的标准差比其均值要大，而垂向轮轨力的标准差比其均值要小100倍左右，说明动车首轮对受到的横向轮轨力的随机性较大。

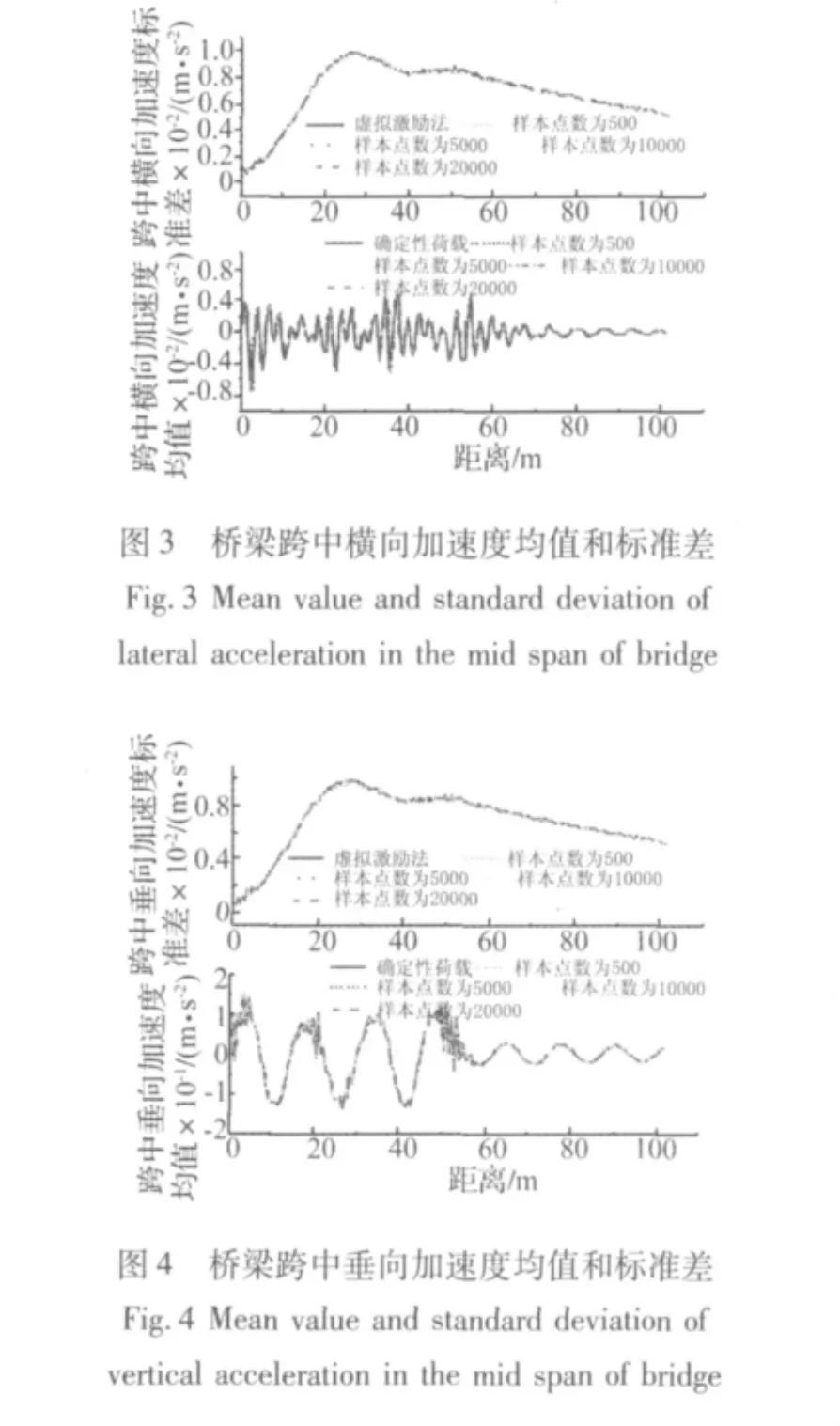
由图1～4可以看到，采用Monte－Carlo法模拟时，桥梁跨中响应的均值和标准差计算结果对于样本点数为500、5000、10 000和20 000区别并不大。

由图5和图8可以看出，动车车体横向加速度以及动车首轮对受到的横向轮轨力的均值和标准差离散性很大，采用Monte-Carlo法模拟时，均值和标准差结果只有在样本点数为20 000时才和由确定性荷载引起的均值以及使用虚拟激励法得到的标准差结果相吻合。

由图6和图7可以看出，动车车体垂向加速度以及动车首轮对受到的垂向轮轨力的均值和标准差的离散型较横向要小，采用Monte-Carlo法模拟时，均值和标准差结果在样本点数为5 000时和由确定性荷载引起的均值以及使用虚拟激励法得到的标准差结果相吻合。

图1～图8验证了本文方法的合理性。

4 数值算例

以一列车通过3跨简支梁为例，讨论车桥系统空间随机动力特性。简支梁截面特性同第3节程序验证中的单跨简支梁截面特性，计算车辆采用德国ICE3高速列车，车辆编组为1动+2拖+1动，采用德国低干扰谱［15］，线路偏心2.5 m，车辆上桥前先以与桥上相同的线路条件行驶100m，待车辆振动趋于稳定后进入桥跨结构。出桥后车辆再行驶50 m。

由第1节的推导可知耦合系统在确定性荷载作用下得到的响应为均值，在虚拟激励作用下得到响应的自功率谱密度，经过积分可以得到其均方差。假设轨道不平顺为高斯平稳随机过程，线性系统下的响应也应该满足高斯分布。根据三倍标准差原理可以确定车桥系统随机响应的最大值和最小值。选取车速为100 km/h、150 km/h、180 km/h、200 km/h、220 km/h、250 km/h、300 km/h、320 km/h 和350 km/h，计算这9 种车速下车桥系统响应的最大、最小值，将其绝对值的最大值作为响应的代表值，分析车桥响应随车速变化的规律。计算频率范围为 0.3－97.2 Hz，频率增量为0.3 Hz。

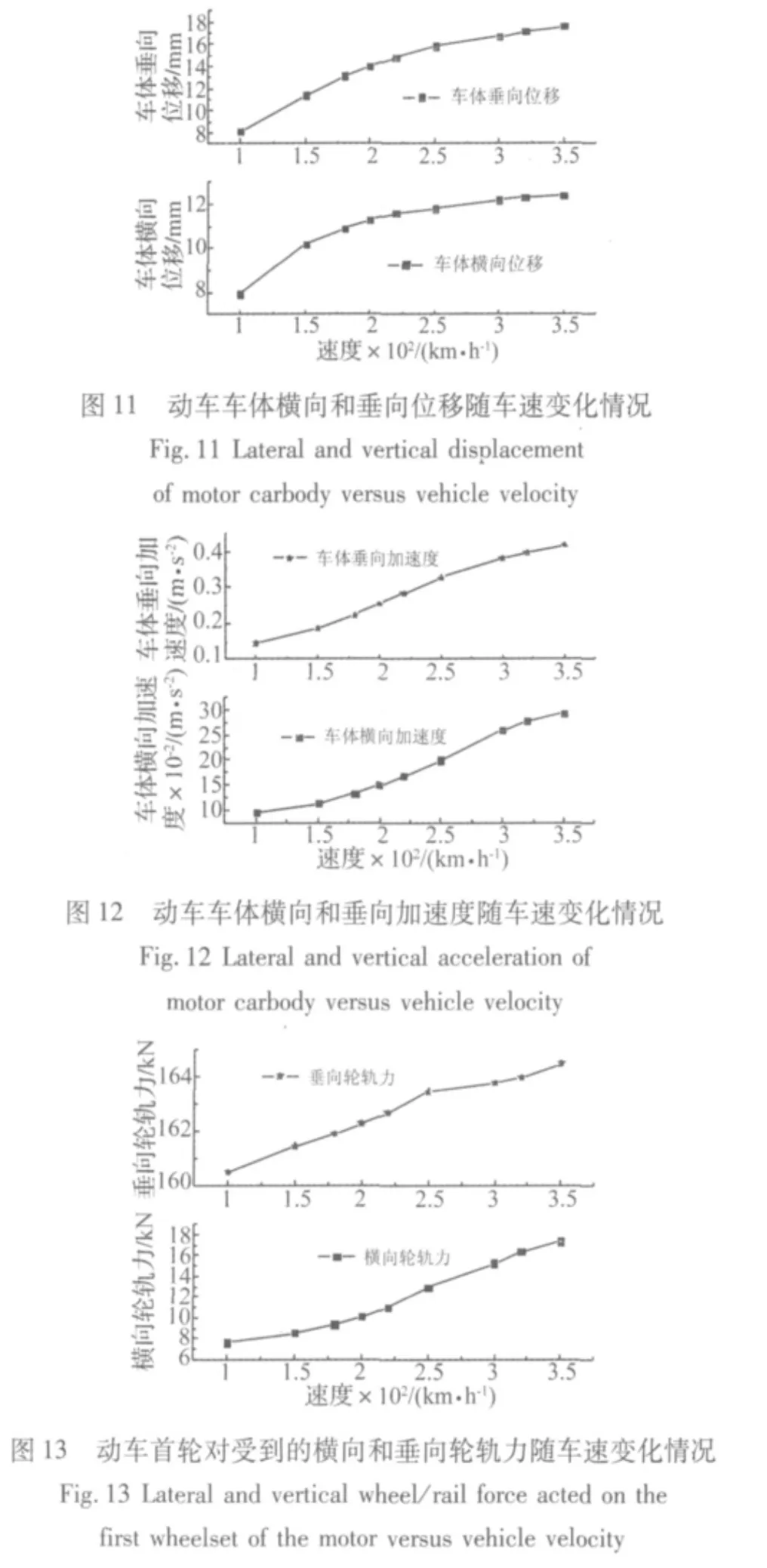
图9～图10为桥梁跨中响应曲线，图11～图12为第一辆动车响应曲线，图13为第一辆动车的首轮对受到的轮轨力曲线。

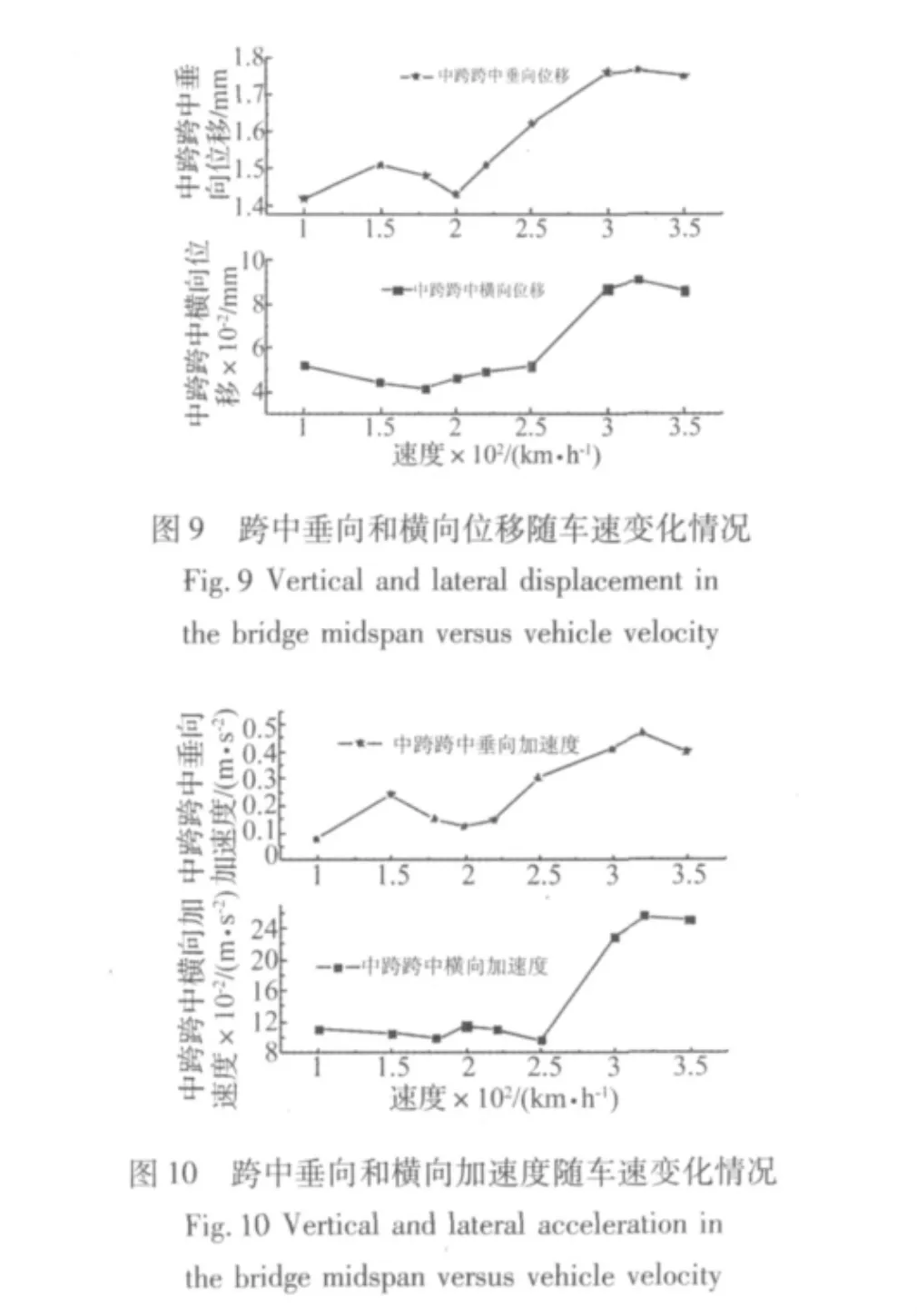
由图9可以看到桥梁跨中横向和垂向位移的绝对值并不是随车速的提高而单调增加的，在车速为320 km/h时响应达到最大值。车速为100～180 km/h时，横向位移的绝对值反而随着车速的提高而减少。车速为150～200 km/h以及320～350 km/h时，垂向位移的绝对值随着车速的提高而减少，在其他速度范围内，随车速的提高而单调增加。

由图10可以看到，桥梁跨中横向和垂向加速度的绝对值均在车速为320 km/h时达到最大值。横向加速度的绝对值在车速为180～200 km/h以及250～320 km/h时，随着车速的提高而单调增加，其余车速范围内，横向加速度的绝对值随着车速的提高反而减少。对于跨中垂向加速度的绝对值而言，在车速为100～150 km/h以及200～320 km/h时，响应随着车速的增加而增加，在其余车速范围内，响应随车速的增加而减少。

由图11～图13可以看到，车体响应的绝对值以及动车首轮对受到的轮轨力的绝对值均是随着车速的提高而增加。

5 结论

本文采用虚拟激励法对空间车桥耦合系统的随机性进行分析，根据三倍标准差原理得到车桥响应的最大、最小值，并取其绝对值的最大值做为响应的代表值，以三跨简支梁为例，讨论桥梁、车辆在不同车速下随机响应的变化规律。得到结论如下:

(1)桥梁跨中横向响应、车体加速度以及横向轮轨力的随机性较大，做为车桥系统的主要激励之一的轨道不平顺是一随机过程，是其主要影响因素;

(2)桥梁跨中响应的绝对值并不是简单得随着车速的提高而单调增加;

(3)车体响应的绝对值以及动车首轮对受到的轮轨力的绝对值均是随着车速的提高而单调增加的。

［1］ Fryba L.Non-stationary response of a beam to moving random force［J］.Journal of Sound and Vibration，1976，46(3):328－338.

［2］ 孙 璐，邓学钧.移动的车辆随机荷载作用下梁桥的瞬态响应［J］.振动与冲击，1997，16(1):62－68.

［3］ Wang R T，Lin T Y.Random vibration of multi-span Timoshenko beam due to a moving load［J］.Journal of Sound and Vibration，1998，213(1):127－138.

［4］ 夏 禾，张宏杰，曹艳梅，等.车桥耦合系统在随机激励下的动力分析及应用［J］.工程力学，2003，20(3):142－149.

［5］ 晋智斌.车－线－桥耦合系统及车－桥随机振动［D］.成都:西南交通大学，2007:101－124.

［6］ 李军强.演变随机响应问题的统一解法及应用［D］.西安:西北工业大学，2000:57－74.

［7］ 吕 峰.车辆与结构相互作用随机动力分析［D］.大连:大连理工大学，2008:89－136.

［8］ 林家浩.张亚辉.随机振动的虚拟激励法［M］.北京:科学出版社，2006:124－280.

［9］ 张志超.赵 岩.林家浩.车桥耦合系统非平稳随机振动分析［J］.振动工程学报，2007，20(5):439－446.

［10］ 张志超.张亚辉.林家浩.车桥耦合系统非平稳随机振动分析的虚拟激励一精细积分法［J］.工程力学，2008，25(11):197－204.

［11］ Lu F，Lin J H，Kennedy D，et al.An algorithm to study nonstationary random vibrations of vehicle-bridge systems［J］.Computers and Structures，2009，87:177－185.

［12］ 朱 艳，李小珍.车桥时变耦合系统的随机响应分析［J］.武汉理工大学学报，2010，32(9):356－359.

［13］ 王福天.车辆系统动力学［M］.北京:中国铁道出版社，1996:3－4.

［14］ 李小珍.高速铁路列车－桥梁系统耦合振动理论及应用研究［D］.成都:西南交通大学，2000:74－76.

［15］ 翟婉明.车辆－轨道耦合动力学［M］.(第3版).北京:科学出版社，2007:107－108.