理解必要条件优化解题策略

☉湖北省秭归县第一高级中学 胡 俊

综观历次高中数学课程的修改，充要条件的内容都做了保留甚至是强化处理.可反观我们的教学，一般都是详细讲解了充分条件和必要条件的定义，然后给了许多组“条件p，条件q”让学生判断“p是q的什么条件”.显然这样的做法完全弱化了充要条件尤其是必要条件在解题时的思维向导作用.本文从运用必要条件优化解题策略方面谈谈笔者的粗浅看法.

我们知道：若已知“p⇒q”，则q是p的必要条件.所谓q是p的必要条件，即意味着q是p成立的必不可少的条件.尽管我们平时解题时应该寻求的是“题设的充要条件”，但相对于“充要条件或充分条件”而言，“题设的必要条件”往往显得简单、直观和具体，容易解决.同时在寻求的必要条件中，不仅包含题设的充要条件，而且在寻求必要条件的过程中常隐含着问题的解法.因此，我们解决某个问题有困难时，常常可以先寻求题设的必要条件，然后再验证其充分性，从而获得问题的解决.在本文中，笔者例谈利用必要条件解题的两种功能：（1）小题小做，直接求解问题；（2）缩小范围，简化解题过程.

一、小题小做，直接求解问题

分析：若按常规解法，则需要利用f（x）=－f（－x）或者f（x）+f（－x）=0恒成立求解.这样的解法显然对指数的相关运算有较高要求，显得有些“小题大做”了.若是直接利用其必要条件f（1）+（f－1）=0求解出同时注意到本题是填空题，若有解的话只能是这样的解法显然快速简洁得多.

当然，如果本题是一个解答题的话，则还需要验证其充分性，即去证明是奇函数，这就是一件很容易的事情了.

二、缩小范围，简化解题过程

例2（人教版必修5P89例6）要将两种大小不同的钢板截成A、B、C三种规格，每张钢板可同时截得三种规格的小钢板块数如表1所示：

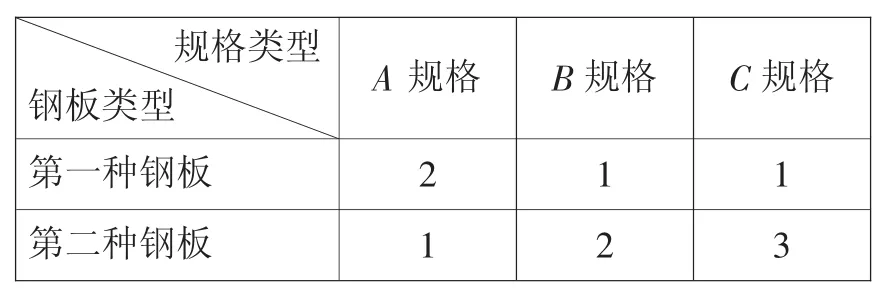
表1

今需要A、B、C三种规格的成品分别15、18、27块，那么需要各裁这两种钢板多少张可得所需三种规格产品，且使所用钢板张数最少？

分析：本题是个典型的线性规划问题，从构建约束条件到用平面区域表示出可行域都很常规.其特别之处在于需要寻求最优整点解，而教材对整点的探求过程又语焉不详，看完教材还是有些不明所以.如果从必要条件去探求就不难理解了.

图1

从以上例子可以看出，利用必要条件解题，就如同破案，先利用蛛丝马迹，确定犯罪嫌疑人的特征（范围），缩小其侦查范围，最后通过筛选抓住罪犯.

需要说明的是，利用必要条件解题并不困难，但对于某个问题的题设而言，其往往有多个不同的必要条件.例1中题设的必要条件就有无数个，最常见的有f（0）=0，本题中由于x=0不在定义域中，所以没有利用其求解.其他的就有f（1）=f（－1），f（2）=f（－2），…等等.显然，较为理想化的题设的必要条件是其自身容易解决，且从其解决过程中又易发现或得到一般性问题的解法.所以，利用必要条件解题的关键是能否找到一个最佳的必要条件.

总之，利用必要条件解题是一个非常有实效的解题策略.我们教师在平时教学过程中，要注意引导学生亲身体验从必要条件的角度考虑问题所带来的好处，让学生懂得必要条件的挖掘和利用是一种解题策略，更是一种生活的智慧.