高三立体几何复习教学中的探究性学习

☉江苏省泰州市民兴实验中学 郭金华

在高三数学立体几何复习中，我们从“以人为本，主动发展”的教学理念出发，将课堂教学设计为探究性学习组织教学，发挥了较好的效果.探究性学习主要分为两个过程：一是问题引动，加强双基；二是主动探究，培养能力.现以立体几何复习中的“角度、距离的计算”一节课的教学为例，分析如下.（限于篇幅，本文主要侧重于二面角）

一、巧设问题，加强基础训练

加强双基，夯实基础是复习目标之一.对于基础知识的复习，由于学生已经有了第一次学习的经历，无论理解的程度如何，总是以为自己是知道的，若仍按照教师提问学生答，教师罗列学生抄，教师归纳学生听的复习方法，势必让学生感到乏味.时间花费多，学生收效少.我们采取“问题引动”法，即在教学过程中，围绕教学内容，设计问题组，引导学生主动复习基础知识，掌握基本方法.

如在“角度、距离的计算”一节复习中，首先设计如下问题：

1.P是边长为a的正三角形ABC所在平面外一点，且PA=PB=PC=a，则二面角P-AB-C的余弦值为_______.

2.已知P为锐二面角α-l-β的棱上一点，PQ⊂α，PQ与l成45°角，与β成30°角，则二面角α-l-β的大小为_______.

设计意图：回顾二面角的计算的常用方法：1.定义法；2.三垂线定理法；3.垂面法.

学生独立完成后，口头回答结果，教师同学生一起反思解题过程，归纳方法及书写格式，通过具体的问题，让学生主动总结基础知识和基本方法.

二、加强探究，培养学生的解题能力

图1

提高素质，培养能力是复习的重要目标，而能力的培养要通过学生的主动探究来实现.我们的做法是：根据教学内容、目标，精选示例，让学生独立思考或通过与同学合作讨论解答，然后师生共同评价.

例1 如图1，在正四棱柱ABCD-A1B1C1D1中，侧棱长为2a，底面边长为a，P是侧棱CC1上一点.

（1）求证：BD⊥AP.

（2） 若CC1=3C1P，求平面AB1P与面ABCD所成的二面角.

让学生独立思考3分钟左右，再口述思路.

生1：第一问用三垂线定理解决即可，第二问用射影法求解，但我没有计算出来.

生3：可以用三垂线定理法，作出二面角的平面角，做法是：延长B1P与BC交点M点，再连接AM，然后过B作BH⊥AM于H，连接B1H即可，∠B1HB就是二面角的平面角.

师：讲得很好，思路很正确.还有没有其他方法呢？

生4：以D为坐标原点，分别以DA、DC、DD1为x、y、z轴建立空间直角坐标系.设底面边长为3.易得平面ABCD和平面AB1P的法向量分别为n1=（0，0，1）、n2=（-1，3，1.5）.

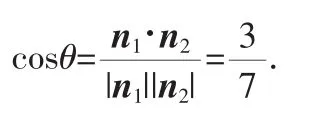
教师进行总结.

这样，通过独立思考，分组协作，互相交流，再通过师生共同解答过程进行反思、比较，使学生主动领悟、吸收、内化解题规律，训练了思维的深刻性、灵活性，在学生主动探究学习的活动中，能力得到了提高，在整个复习过程中达到高考复习数学的总目标.