深入方可浅出——关于一类求椭圆离心率取值范围问题的思考

☉湖北省武汉市东湖中学 冯 炜

有许多问题，我们往往会被其貌似复杂的表面现象所迷惑，以致一叶障目，看不到问题的本质，把握不住规律.这时就需要我们再深入一步，探究其本源，寻求其规律.本文结合以下案例谈谈自己的思考.（1）若椭圆上存在点P，对于左、右焦点求其离心率的取值范围.

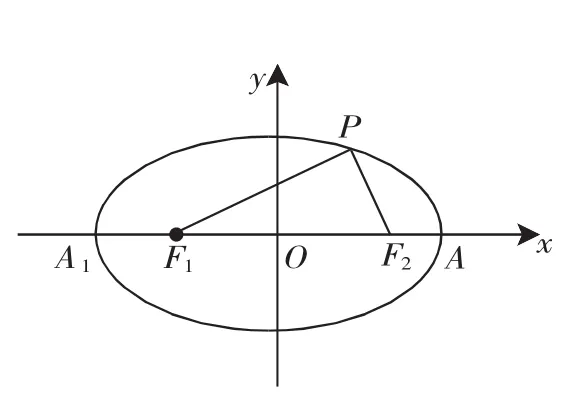
图1

对于（1），我们通常的做法是：设P（x0，y0），利用焦半径公式将转 化 为又

对于（3），焦半径公式就无用武之地了，用上述（2）的思路也将受阻，因此要解决此题只得另想其他方法了.其一种思路为：设P（x0，y0）、A1（－a，0）、A2（a，0），利用“到角公式”计算∠A2PA1的正切值，消去y0后再利用0≤x02＜a2构造不等式后求解得e∈此处解题过程略.

上述三个问题从形式和解法上来看，均互不相同，似乎它们之间没有什么本质的联系.若深入分析，发现它们还是有共同点的，如：点F1、F2或A1、A2都在椭圆的长轴上.那么一般地，任给两点M（1－x1，0）、M（2x2，0）（0＜x1≤a），若椭圆上存在点P，使∠M1PM2=α（900≤α＜1800），求其离心率的取值范围.又该如何处理？

证明：由椭圆的对称性，为讨论简便且不失一般性，可设P点的纵坐标y0＞0.

这样一来，前面的三个问题表面上看似联系不大，解题思路也各异，但其本质是相同的.

在新课改的实施过程中，作为数学教师，需要在平时的教学过程中，引导学生适时地深入一步，尽可能地探究出问题的本源，只有这样深入才可以做到浅出.