例谈利用几何画板解决圆的问题

☉江苏省南京市大厂高级中学 张路民

我们知道当一条线段绕着它的一个端点在平面内旋转一周时，它的另一个端点的轨迹叫做圆.我们在解决圆的相关题目时常常会遇到一些动圆或者是隐形圆.这类问题往往处理起来比较棘手，原因主要在于它们太抽象，但如果我们能借助于几何画板将其画出甚至动起来就变得很形象了，当然问题也就容易解决多了.下面笔者举两个例题加以分析.

一、利用几何画板解决动圆问题

例1 如图1，在直角坐标系xOy中，A（a，0）（a>0）、B（0，a）、C（-4，0）、D（0，4），设△AOB的外接圆的圆心为E，点P在圆E上，使△PCD的面积等于12的点有且只有三个，试问：这样的⊙E是否存在？若存在，求出⊙E的标准方程，若不存在，说明理由.

分析：本题中的⊙E显然是一个动圆，随着a的取值的变大，⊙E也会逐步变大，因此若借助于几何画板进行演示将会非常有助于问题的解决.

图1

由平行线性质我们知道：两条直线平行，其中一条直线上的任意点到另一条直线的距离相等.

图2

故满足条件的平行线有两条，方程分别为l1：x-y+10=0，l2：x-y-2=0.又因为点P在⊙E上，故所求点即为圆与直线l1、l2的交点

借助于几何画板加演示.如图2，作出直线l1、l2作△AOB的外接圆，将圆小慢慢变大，当圆与直线l1l2有三个交点时即为所求圆

所以这样的⊙E存在，其程为：（x-5）2+（y-5）2=50.

评注：本题借助于几何画板通过辅助直线l1、l2将动圆问题形象的展示出来，使得原本非常抽象的问题具体化，我们在改变圆的大小的过程中能够很直观的感受到点P从无到有的过程.

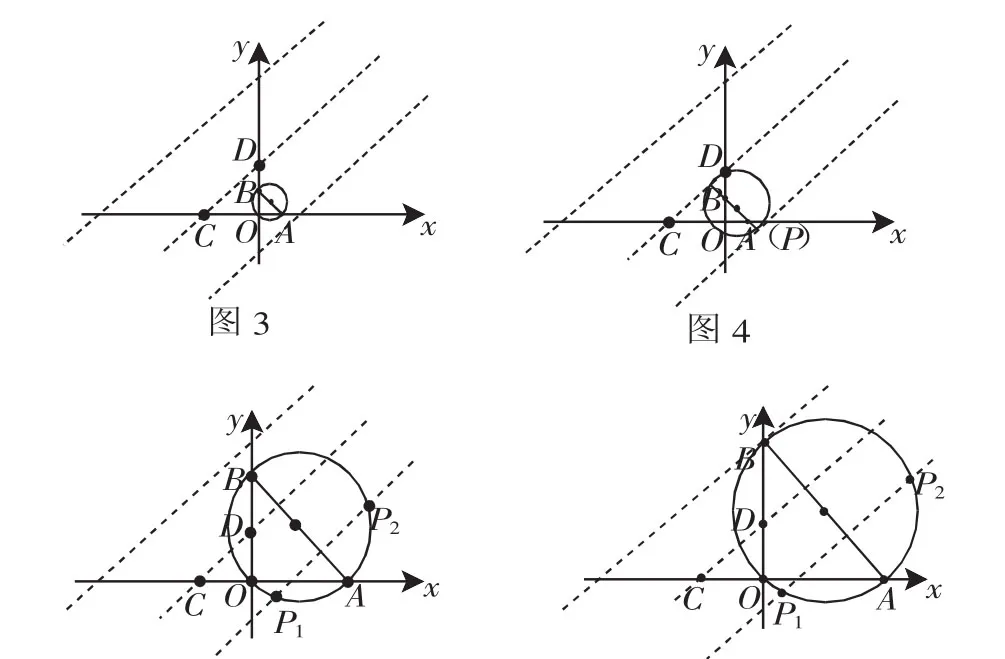
图5图6

图7

延伸：经进一步研究还能得到以下结论.

这样这道题不仅得到了非常完美的解决，而且还得到了进一步的延伸.在这道题的解决过程中，两条辅助直线起到了非常重要的作用，它们让我们很清晰的观察到了点P从不存在到存在、从少到多的过程，把原本不太容易下手的问题变得简洁.

二、利用几何画板，借助“隐形”圆解决其他问题

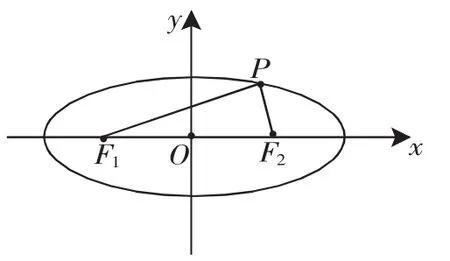
图8

分析：本题解决的关键是如何定位∠F1PF2为钝角.确定角的大小一般可以利用余弦定理或向量的数量积等，就本题而言，虽然可以实施但较复杂.通过几何画板的动态演示，我们发现圆有如下性质：圆上一点与任意一条直径的两个端点连接（该点不在此直径上）构成的角为直角；若该点在圆内则构成的角为钝角；若该点在圆外则构成的角为锐角.

由圆的性质，可知分别以点P1、P2、P3、P4为顶点与F1、F2连接构成的角为直角.

椭圆上点P1、P2之间以及P3、P4之间的点同时在圆内，故以它们为顶点连接F1、F2构成的角为钝角，符合题意.

所以所求点P介于P1、P2之间以及P3、P4之间.

图9

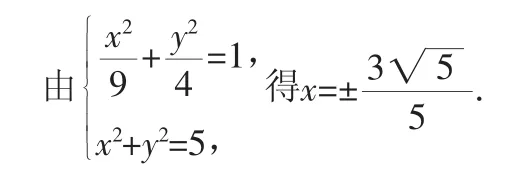
评注：本题表面上看不出与圆有任何关系，但通过分析发现题中隐含着一个圆，借助几何画板更加能够直观形象地体现出来，对问题的解决起到了很大的辅助作用.

计算机辅助教学是随着计算机技术的发展而形成的现代教育技术.《几何画板》引入数学课堂教学能体现出以下主要作用.

（1）有助于提高课堂效率，把抽象的知识形象化.

（2）有助于提高课堂教学效果.由于情况的快速反馈，老师讲课时更具有针对性，并能及时调整教学内容和节奏.

（3）有助于培养学生敏捷思维和观察问题、分析问题、解决问题的能力.