平面向量数量积常见考点剖析

☉江苏省东台市三仓中学 刘加元

向量是解决数学问题的重要工具，而数量积又是向量内容的重点，所以数量积是高考考查的热点，以基础题和中档题为主，现以2011年高考题为例说明如下.

一、求数量积

例1 已知两个单位向量e1、e2的夹角为，若向量b=e-112e2，b2=3e1+4e2，则b1·b2=_________.

解：b1=e1-2e2，b2=3e1+4e2，则b1·b2=（e1-2e2）·（3e1+4e2）=3e12-2e1·e2-8e22.又因为e1，e2为单位向量，其夹角为，所以

评注：本题考查平面向量知识，重点考查向量数量积的运算，以及简单的计算能力.

A.1 B.2 C.3 D.4

解：a+b=（1，k）+（2，2）=（3，k+2）.

由a+b与a共线，得k+2-3k=0，解得k=1，则a·b=（1，1）·（2，2）=4.应选D.

评注：本题考查向量共线、向量数量积的坐标运算及简单的运算求解能力.

二、求向量的模或模的最值

例3 已知单位向量e1、e2的夹角为60°，则|2e1-e2|=__________.

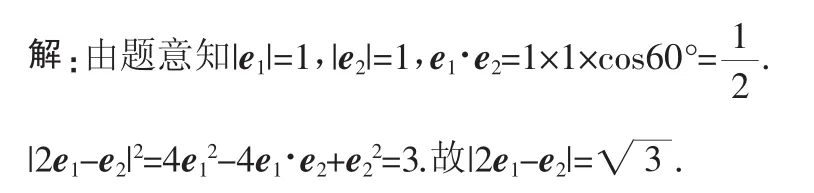
评注：本题主要考查向量的模、数量积的运算.

例4 若a、b、c均为单位向量，且a·b=0，（a-c）·（b-c）≤0，则|a+b-c|的最大值为（ ）.

解：由a·b=0，（a-c）·（b-c）≤0，得-a·c-b·c≤-c2=-1.

官修史书往往借对前一个朝代的总结来确立政权合法性的手段。薛居正等人所修的 《旧五代史》由于是奉敕所修的正史，代表官方的立场，虽然还是肯定了冯道的忠于职守，也不吝啬对其私德作出正面的评价，这很有可能与参与修史之人多经历过五代乱世有关；但还要顾忌到对社会风气的影响，用忠孝节义的标准批评一番。

|a+b-c|2=a2+b2+c2+2a·b-2a·c-2b·c=3+2-（a·c-b·c）≤3-2=1，故|a+b-c|的最小值为1.应选B.

评注：本题主要考查向量的数量积及向量模的运算，难度较大.

三、求向量的夹角或夹角的范围

例5 已知|a|=|b|=2，（a+2b）·（a-b）=-2，则a与b的夹角为__________.

解：由已知条件（a+2b）·（a-b）=-2，得：|a|2+a·b-2|b|2=4+2×2×cosθ-2×4=-2，得

评注：本题考查向量的数量积运算，以及向量的夹角公式，稍有难度.

例6 若平面向量α、β满足|α|=1，|β|≤1，且以向量α、β为邻边的平行四边形的面积为，则α与β的夹角θ的取值范围是_________.

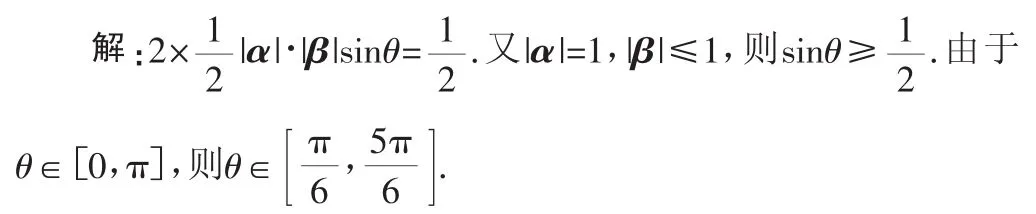
评注：本题考查平面向量的基础知识，要注意向量夹角的取值范围，难度适中.

四、垂直问题

例7 已知a与b为两个不共线的单位向量，K为实数，若向量a+b与向量Ka-b垂直，则K=_________.

解：由题意知（a+b）·（Ka-b）=0，即K+（K-1）a·b-1=0，所以（K-1）a·b=1-K.因为a与b不共线，所以K-1=0，即K=1.

评注：本题考查向量的数量积运算及向量互相垂直的条件的应用，难度适中.

五、综合交汇

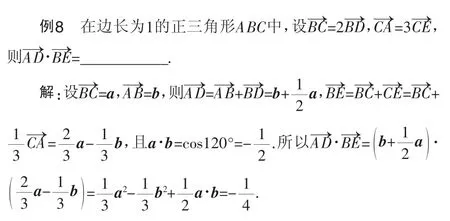
评注：本题考查向量的线性运算和数量积运算，主要考查学生的运算能力及利用数形结合思想解决问题的能力.