单位向量用途大
2018-11-23顾珊岚
新高考·高一数学 2018年1期
顾珊岚


单位向量是长度等于1的向量.它在向量大家庭中的地位举足轻重.对有些问题,特别是关于角平分线的问题,若能根据其特点构造单位向量,就可迅速地找到解题的切人点,使解题过程简捷,几何背景直观,运算化繁为简,令人有四两拨千斤之感.
通过引例我们发现,单位向量与角平分线有着密切的联系,两个单位向量的和具有这样的几何性质:
当问题的呈现形式与单位向量、角平分线有着直接或隐含的联系时,借助于以上性质,就可以达到快速而正确地解决问题的目的.
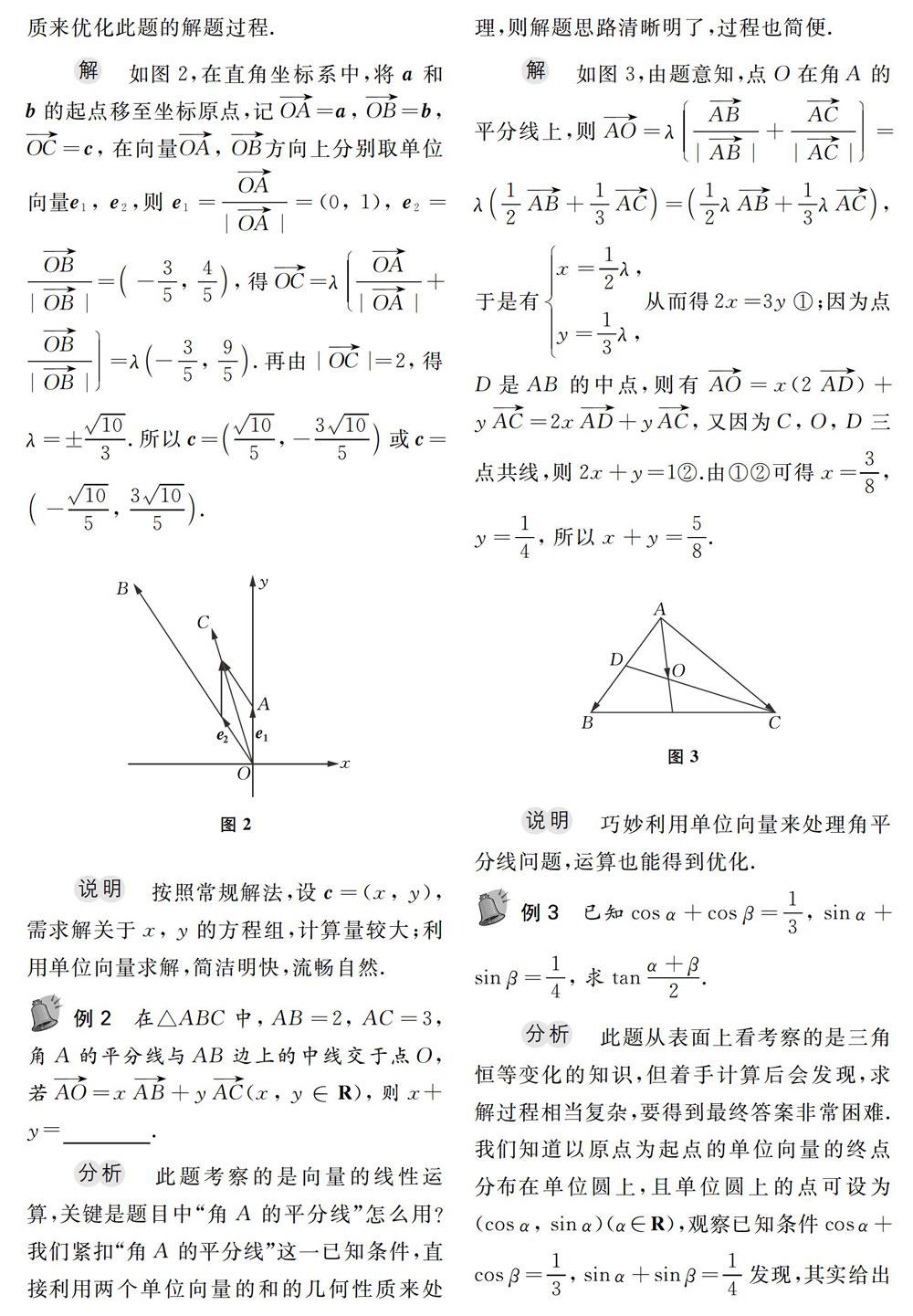
分析 此题從表面上看考察了向量的模和向量的夹角问题,可运用学过的公式,从代数角度进行求解.从几何角度,我们发现“夹角相等”与角平分线有联系,所以可以通过构造单位向量,利用单位向量和的几何性质来优化此题的解题过程.
说明 按照常规解法,设c=(x,y),需求解关于x,y的方程组,计算量较大;利用单位向量求解,简洁明快,流畅自然.
分析 此题考察的是向量的线性运算,关键是题目中“角A的平分线”怎么用?我们紧扣“角A的平分线”这一已知条件,直接利用两个单位向量的和的几何性质来处理,则解题思路清晰明了,过程也简便.
说明 巧妙利用单位向量来处理角平分线问题,运算也能得到优化.
说明 从两个单位向量的和的几何性质出发来分析解答,避繁就简,一气呵成.
由此可见在解决与角平分线有关的问题时,如果仅仅拘于传统思维方式思考,则头绪繁杂,不易突破;若抓住问题的内在联系,运用构造单位向量这种思维模式,则可以达到事半功倍的效果,当然,在解决问题的过程中应因题制宜,灵活运用,恰当选择,方可立于不败之地.
