电力系统紧急情况下的动态分区和自主解列策略

宋洪磊 吴俊勇 吴林峰

（北京交通大学电气工程学院 北京 100044）

1 引言

随着电力系统的快速发展，电网之间的联系越来越紧密，电网的规模也越来越大，这也带来了严重的暂态稳定问题。一般的大停电事故表明，一些小概率的级联事故可能引起系统失稳，从而导致系统崩溃，同时，一些小概率的极端外部灾害事件也会导致系统的崩溃，从而造成灾难性的大停电事故。为了降低停电风险，可在正常运行和缓慢相继开断阶段中采用预防控制，在快速相继开断阶段采用紧急控制，在振荡阶段中应用校正控制，在发生停电后实施恢复控制[1]。

在电网处于高度危险期间，由于相继开断非常快，已经无法在线完成N-1扫描，这时可以采取动态分区，主动解列的方法实施紧急控制。实际电力系统都是分层分区的，而且分区往往是按行政区划静态形成的，在电网正常和故障后的蔓延阶段，紧急控制通过监视各分区内主要节点以及各分区间联络线的运行状况，快速判断出整个电网的安全性，进行动态安全预警，并且按照合适的准则对静态区域进行动态组合，将故障隔离在一个最小的区域内，并在该区域内在线实施切机切负荷以实现功率的自平衡，降低故障的影响范围，一旦发现大电网有发生瓦解的危险，即按照制定的最优分区方案进行主动解列。

文献[2-3]根据电力系统的动态特性表现为快慢两个时间尺度，建立双时间尺度的奇异摄动模型对慢同调现象进行了深入研究，提出了基于慢同调的机组分区方法；文献[4-5]在先前研究的基础上，提出了基于慢同调理论的电网解列控制策略，利用深度优先搜寻技术，对化简的网络搜索最小割集，寻找电网的薄弱边界。文献[6-7]提出了两种搜索分区割集的方法，但遍历搜索都会有组合爆炸的问题，在时间上往往不能满足紧急控制的要求；文献[7-10]利用 Laplace矩阵的半正定奇异性和实数特征根，提出了一种快速高效搜索分区割集的 Laplace分区策略。但该策略以线路有功功率的绝对值为权重，没有考虑功率的方向问题。

本文将慢同调理论和图论KWP（K-Way Partition）方法相结合，提出了一套完整、协调的大电网智能主动解列控制策略。通过慢同调分区，将系统中振荡模式相近的发电机组分成最优的区域，把分区后的发电机组区域聚合成若干虚拟的发电机群节点，最大限度地缩小了最佳解列割集的搜索空间。在充分研究了 Laplace分区策略的基础上，提出了新的加权指标，对 Laplace分区策略进行了改进。结合前两个分区策略，并考虑有功功率的方向性，提出了在 Laplace分区策略及其改进分区策略得到的分区割集附近，进行邻域搜索的启发式邻域搜索分区方法。最后综合这三种分区方案，在各区域内采用启发式就近削负荷方法进行功率自平衡，从而得到全系统总的削负荷量最小的最优分区策略。

2 慢同调分群算法

慢同调方法是以多时间尺度理论和奇异摄动理论为基础，通过构造电力系统双时间尺度的奇异摄动模型对电力系统的慢同调现象进行深入研究。该方法主要是对系统的状态矩阵求取特征值和特征向量，分析系统潜在的振荡模式，获取发电机之间存在的弱联系，从而对同调机群以及网络的薄弱环节进行识别。

2.1 数学模型

基于慢同调方法的发电机群同调性的识别，是采用线性化的电力系统模型为基础，提出一种完善的电力系统发电机组慢同调分群算法。

忽略凸极效应、励磁绕组暂态及阻尼绕组的作用，同步电机采用经典二阶模型，则发电机转子运动方程可以表达为

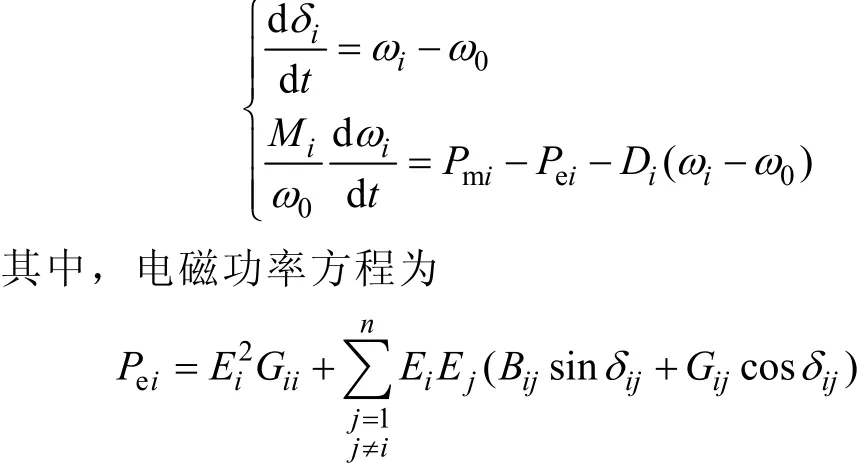
式中，i=1,2,…,n；Mi为第 i台发电机转子的运动惯性时间常数；δi为第 i台发电机的转子角，rad；ωi为第 i台发电机的转速，rad/s；ω0为同步转速，rad/s；Pmi为第i台发电机的机械输入功率，是一个常数；Pei为第i台发电机的电磁输出功率；Di为阻尼常数，s/rad；Ei、Ej为第 i台和第 j台发电机暂态电抗后的电动势的幅值，=E∠δ；Yij=Gij+jBij为并入负荷阻抗和发电机暂态电抗后，收缩到发电机内电动势节点的导纳矩阵元素。

忽略阻尼常数的影响，将公式在各个发电机功率及角度的稳态值Pei0，δi0附近进行线性化，可以得到

式中，M是系统中发电机惯性时间常数的对角阵，M=diag （M1,M2,⋅⋅⋅,Mn）；K是系统状态矩阵，其中

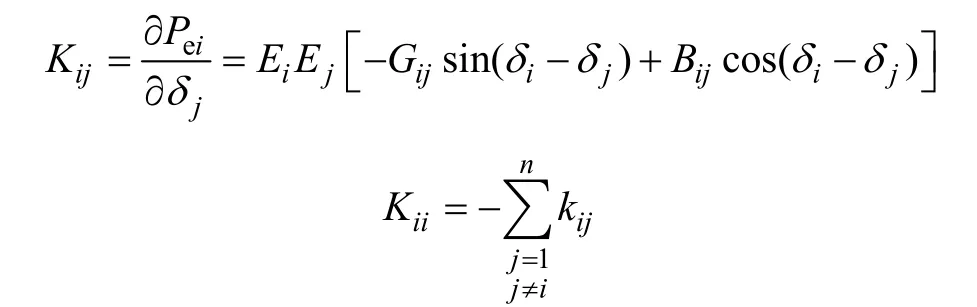
2.2 慢同调分群算法

基于慢同调分群算法的主动解列，首先是通过系统状态矩阵的特征值识别出发电机群的r个最优分群数，即系统的r个慢模式，然后利用高斯消去法对发电机进行分群。其慢同调的分群算法步骤具体如下：

（1）确定最优的慢同调聚合分区数。求取矩阵A的全部特征值，并按其虚部（即振荡频率）绝对值从小到大排列所有的特征值为发电机的台数。根据电力系统多时间尺度特征原理，m的值越小说明系统的时间尺度特征越明显，对于慢同调分区的区域性也越明显。这样可以得到慢模式组 σr=｛λ1, λ2,…λr｝，并得到对应的特征向量空间U=（u1, u2,… ur），即最优的慢同调聚合分区数为r。

（2）得到慢同调参考机组。对于特征向量U=（u1, u2,… ur）做列主元高斯消去法，得到 r组线性无关的向量，其对应的行选定为进行慢同调聚合的参考机组，并得到慢模式组σr所对应的参考机组向量 U1。

（3）计算分群矩阵 L。对于特征向量矩阵U=（U1U2）T，则分群矩阵

（4）发电机组分群识别。根据分群矩阵 L每行的最大值，将其他的发电机组分配到相应的参考机组中，形成慢同调的分群区域。

3 Laplace分区策略

Laplace分区策略是以线路有功功率的绝对值为权重，快速寻找出分区时割集线路有功功率的绝对值之和较小的分区方案。

3.1 Laplace分区策略的基本定义

（1）将电力系统按照一定的方法主动解列成一定数量的小系统，称为分区；对应的方法称为分区策略。

（2）电力系统分区时，要断开一定数量的线路，使系统解列成两个区域，此时断开的线路称为割集。

（3）电力系统解列成两个区域时，从一个区域流向另一个区域的功率之和，称为净不平衡功率。

（4）V={v1,v2,⋅⋅,vn}是节点集，A=[aij]为网络图的邻接矩阵，其中：当vi和vj之间有支路连接时，aij等于该条支路的有功功率的绝对值；当vi和vj之间没有支路连接时，aij=0。

（5）D=[dii]为网络图的对角矩阵，其中，对角元素dii等于邻接矩阵A的第i行元素之和。

3.2 Laplace分区策略算法

第一步：将电力网络转化为一个边带权重的无向图G。

（1）计算电力系统的潮流。

（2）将电力网络转化为一个边带权重的无向图G。

（3）电力网络的每个节点是图G的一个顶点。

（4）电力系统的每一条传输线是图 G的一条边。

（5）图 G的每条边的权重是根据相应传输线的电力潮流功率的绝对值来确定的。

第二步：计算 Laplace矩阵 Q，它的特征值以及相应的特征向量。

（1）计算图G的邻接矩阵A和对角矩阵D。

（2）计算图G的Laplace矩阵，Q=D-A。

（3）计算Laplace矩阵Q的k个最小的特征值1λ,2λ,⋅⋅,kλ。

（4）计算特征值1λ,2λ,⋅⋅,kλ对应的k个特征向量 x1,x2,⋅⋅,xk。

第三步：由Laplace矩阵Q的前k个特征向量构成分区向量

（1）通过前 k 个特征向量 X=(x1, x2,⋅⋅, xk)来计算分区矩阵是一个对角矩阵，满足是矩阵 X的第 i行标准化后的元素之和）。

第四步：选择k个顶点作为k个分区的k个种子。

（1）选择一个顶点作为第一个种子。

（2）让向量“seeds”存储这 k个分区的 k个中心节点。

（3）让 seeds={S1}去存储第一个种子作为第一个中心节点。

（4）当|seeds|＜k时，按如下操作：

①寻找满足{max cos(v, Si)}最小的一个新顶点v，如：选择的新的种子应该选择尽可能远离原来已经选择的中心节点。cos(v, Si)的值是在分区矩阵中获得的。

②存储新的种子到向量，seeds={seeds}∪{v}

③在所有的k个种子选择完之后，向量变成了seeds=(S1, S2…S1)，Si为区域 i的中心（i=1,2,⋅⋅,k）。

第五步：将剩余的n-k个顶点归类到这k个区域，并得到这k个分区。

（1）i从1到n-k循环。

（2）寻找索引 j，使得 cos(Sj, vi)最大，1≤j≤k。找到的种子Sj则是所有k个种子中与顶点vi距离最近的。

（3）使p={A1, A2, …, Ak}为分区设置，则区域Aj=Aj∪{vi}。

第六步：根据分区节点，得到各区之间的割集和净不平衡功率。

（1）任取两分区的节点，从这两分区中各取一个节点进行组合，以该组合的两个节点标号分别代表行和列，若邻接矩阵A的该组合对应位置的值不为零，即该组合对应的线路即为割集线路，割集线路的有功功率的代数和即为该分区的净不平衡功率。

（2）同理求出其他各分区之间的割集矩阵；若两分区之间不存在割集，则说明这两分区不相邻。

3.3 改进的Laplace分区策略

考虑到节点之间的联系与线路上传输的功率以及电气距离都有一定的关系，故本文提出一个新的权重指标|P|/XL，即一条线路上传输的有功功率P绝对值越大，线路电抗XL越小，说明该线路的两个节点联系越紧密，权重也越大。以该权重替代前述的线路有功功率绝对值，同样按照 Laplace分区策略算法，快速寻找出分区时切割的线路权重之和较小的分区方案，并通过后续算例的验证来说明该方案的有效性。

4 启发式邻域搜索分区策略

通过对 Laplace分区策略和其改进分区策略进行分析可以看出，这两种分区策略都未考虑线路有功功率的方向。在采取紧急控制时，电力系统往往是比较脆弱的，此时稳定性是最重要的。如果分区后净不平衡功率很大，则在调整功率平衡时，必然会对系统造成很大的冲击。故本文提出了考虑线路有功功率方向的启发式邻域搜索分区策略，即寻找净不平衡功率较小的分区割集。Laplace分区策略和其改进分区策略是在电力系统网络联系比较薄弱处进行分区，启发式邻域搜索分区策略就是在这个薄弱处附近考虑线路有功功率的方向，寻找净不平衡功率更小的分区方案。

由于电网比较庞大，要搜索所有可能的分区方案和割集存在组合爆炸问题，而该分区策略要应用于紧急控制，对分区策略的计算时间有严格的要求，故要寻找出一种快速、高效的搜索方法。基于上述考虑，本文在上述两种分区方案和割集算法的基础上，将节点度的概念应用于该搜索方法中，采用分组的方法，使得计算时间大大缩短，以满足紧急控制的要求。

4.1 启发式邻域搜索分区策略的基本定义

（1）电力系统分区时，要断开一定数量的线路，使系统解列成两个区域，此时断开的线路对应的节点称为故障节点。

（2）与故障节点通过一条线路直接相连的节点称为1度节点；与1度节点通过一条线路直接相连的节点称为2度节点（1度节点除外）；依此类推。

4.2 启发式邻域搜索分区策略的算法

（1）根据 Laplace分区策略及其改进分区策略求出对应的两个基本割集。

（2）每个割集中，割集的每一条线路对应一个分组。

（3）对于割集中的每一条线路，在其某个故障节点附近搜索，将与该故障节点直接相连（除去对应的割集线路）的线路作为该分组的一个元素；将与该故障节点的1度节点直接相连的线路（除去前一个元素中包含的线路）作为该分区的另一个元素；按此方法搜索一定范围的线路，形成分组的元素；同理搜索另一故障节点另一侧的线路作为同一分组的元素，同时对应的割集线路也是该分组的一个元素。

（4）按照（3）的方法，同理求出所有割集线路对应的分组。

（5）将这些分组并列处理，从每个分组中取一个元素，形成一个线路集合，由于每个数组元素有多条线路，可能存在两个数组中包含同一条线路的情况，将该线路集合进行处理，重复的线路只保留一次，处理后的线路集合形成一个新的割集。

（6）对于这两个基本割集，寻找出所有的“邻接”割集。考虑割集线路有功功率的方向，计算基本割集和“邻接”割集的净不平衡功率，保留比对应基本割集的净不平衡功率小的割集。

5 就近启发式削负荷策略

电力系统在分区解列控制中断开的线路不止一条，故分区后各个子分区中的故障为多重故障，即在大规模电力系统中，元件故障后通常只在故障元件附近的局部区域出现违背静态安全约束的情况，系统的调整和校正措施也着重在这部分进行。系统故障后按照就近原则在故障元件附近的一定区域内通过潮流追踪搜寻能有效缓解系统故障情况的负荷削减节点集。

对于运行调度人员最关心的并不是在全系统范围内采取调整措施使系统恢复到一个最优的安全经济运行点，即考虑的主要因素不是系统运行状态的最优经济性，而是如何在最短时间内将系统恢复至安全状态并尽可能将故障的影响限制在最小范围内，使系统达到新的安全运行点的理想方案是在过负荷线路和电压异常的母线附近采取尽可能少的调整措施。

当电力系统主动解列成两分区时，各个分区都存在净不平衡功率；就近启发式分区策略首先调整最近的发电机的输出，然后调整更远的发电机；如果这区域仍存在功率不平衡，则由近及远削减负荷；直至功率平衡；然后进行电力潮流分析并检查线路功率和节点电压是否越限。如果存在越限，则再次调整发电机和负荷直至系统潮流满足要求。

6 Laplace混合分区算法

总结 Laplace混合分区算法如下流程如下图所示。

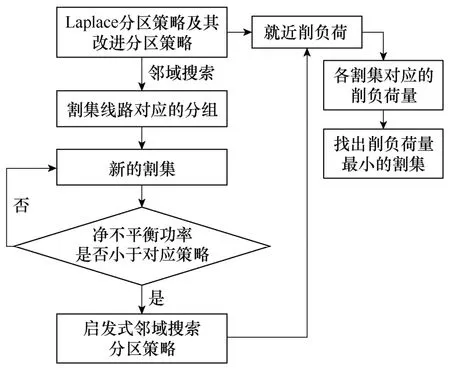
图 Laplace混合分区算法的流程图Fig.Flow chart of hybrid Laplace partition algorithm

（1）基于 Laplace分区策略及其改进策略，得到两个基本割集。

（2）基于启发式邻域搜索分区策略，得到净不平衡功率比对应分区策略小的“邻接”割集。

（3）基于就近启发式削负荷策略，计算各个割集对应的削负荷量，削负荷量最小的割集是最佳选择，并应用于主动解列控制。

7 算例分析

本文提出的算法中，应用慢同调分群算法对发电机组分群，整个系统的发电机组进行振荡模式识别，形成系统线性化的状态方程，并通过求取状态矩阵的特征值，判断出慢模式值。运用本文提出的系统慢模式和发电机组分群间存在的关系，确定系统的最优分群数。在识别同调机组分群后，要对相关的母线和传输线路进行聚合。这里提出同调机群关联节点、同调机群非关联节点和同调机群最小二叉树割集的概念。

为了进一步验证本文提出的算法的有效性，将以IEEE 118节点系统为例进行说明。利用本文提出的慢同调分群算法，此系统的慢模式有9个，具体的发电机组聚合见表1。

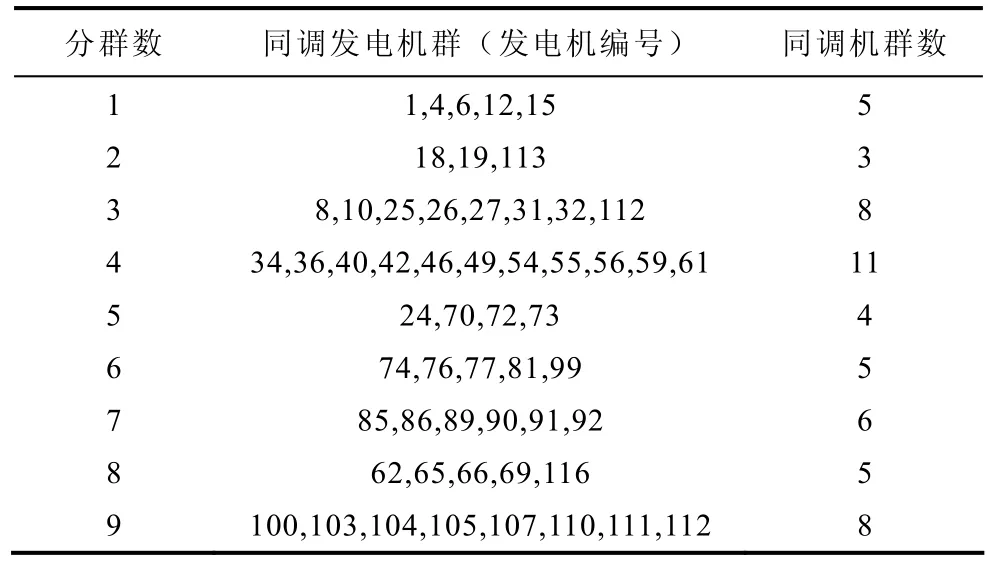
表1 同调发电机分群结果Tab.1 The results of generators grouping

将网络中各母线向发电机节点聚合，形成发电机虚拟节点后，再利用 Laplace分区策略，改进的Laplace分区策略和考虑有功功率方向的领域搜索分区策略，得到的二分区结果见表2。

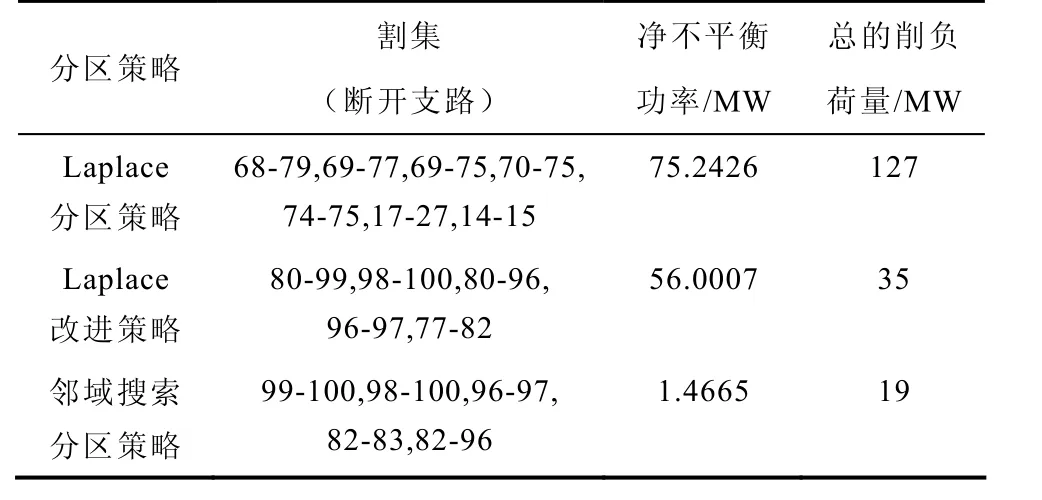
表2 IEEE118节点系统分区情况Tab.2 Hybrid Laplace partition results on IEEE118 grid

通过在 IEEE 118节点系统上应用本文提出的主动解列控制算法进行分析表明，在 Laplace分区策略及其改进分区策略得到的分区方案附近分别存在净不平衡功率比对应方案更小的分区割集，且最终的削负荷量也比对应的方案小，即此时启发式邻域搜索分区策略搜索到的分区方案为最优，对应割集为最优割集；同时可以看出该最优割集是在改进Laplace分区策略附近搜索得到的，即改进Laplace分区策略为寻找最优割集提供了方向，且改进Laplace分区策略得到的分区方案的削负荷量比Laplace分区策略要小，不仅证明了本文提出的基于慢同调分群和 KWP图论分区算法的适用性，也证明了在分区中考虑功率方向问题的重要性和启发式邻域搜索分区策略的有效性。

8 结论

本文探讨了一种主动解列控制的新方法，利用慢同调分群算法将系统中的发电机组聚合成若干虚拟发电机群节点，最大限度地减小割集的搜索空间，在考虑拓扑结构和潮流方向的基础上，将网络中的其他节点向虚拟发电机群节点聚合，并在 Laplace分区策略的基础上提出了一个新的权重指标来衡量两个相邻节点之间的“距离”，以改进 Laplace分区策略。为了考虑有功功率的方向问题，提出了在Laplace分区策略及其改进分区策略得到的分区割集的邻域搜索可能的割集的启发式邻域搜索分区方法。在IEEE 118系统上的应用结果表明，慢同调分群算法和虚拟发电机节点聚合可以在保证发电机同调性的基础上，大大减小了搜索空间和提高了计算的速度，具有很好的适用性和可靠性。

[1]薛禹胜, 费圣英, 卜凡强.极端外部灾害中的停电防御系统构思(1): 新的挑战与反思[J].电力系统自动化, 2008, 32(9): 1-6.Xue Yusheng, Fei Shengying, Bu Fanqiang.Upgrading the blackout defense scheme against extreme disasters (partⅠ): New challenges and reflection[J].Automation of Electric Power Systems,2008, 32(9): 1-6.

[2]Ranjit A Date, Joe H Chow.Aggregation properties of linearized two-time-scale power networks [J].IEEE Transactions on Circuits and System, 1991, 38(7):720-730.

[3]Joe H Chow, Petar V Kokotovic.Time scale modeling of sparse dynamic networks [J].IEEE Transactions on Automatic Control, 1985, 30(8): 714-722.

[4]You Haibo, Vijay Vittal, Wang Xiaoming.Slow coherency-based islanding [J].IEEE Transactions on Power Systems, 2004, 19(1): 483-491.

[5]Yang Bo, Vijay Vittal, Gerald T Heydt.Slowcoherency-based controlled islanding-a demonstration of the approach on the august 14, 2003 blackout scenario [J].IEEE Transactions on Power Syetems,2006, 21(4): 1840-1847.

[6]于红斌, 李孝安.基于分区策略的蚂蚁算法[J].微处理机, 2007, 3: 78-80.Yu Hongbin, Li Xiaoan.Ant algorithm based on separating areas strategy [J].Microprocessors, 2007,3: 78-80.

[7]Chan P K, Schlag M, Zien J.Spectral K-way ratio-cut partitioning and clustering [J].IEEE Transactions on Computer-Aided Design of Integrated Circuits Systems, 1994, 13(9): 1088-1096.

[8]Hao Li, Gary W Rosenwald, Juhwan Jung, et al.Strategic power infrastructure defense[J].Proceedings of the IEEE, 2005, 93(5): 918-933.

[9]Hall K M.An r-dimensional quadratic placement algorithm [J].Management Science, 1970, 17:219-229.

[10]Barnes E R.An algorithm for partitioning the nodes of a graph [J].Algorithm and Discrete Method, 1982,3: 541-550.

[11]赵渊, 周家启, 周念成, 等.发输电系统可靠性评估的启发式就近负荷削减模型[J].电网技术, 2005,29(23): 34-39.Zhao Yuan, Zhou Jiaqi, Zhou Niancheng, et al.A heuristic approach to local load shedding scheme for reliability assessment of composite generation and transmission system[J].Power System Technology,2005, 29(23): 34-39.

[12]郭永基.电力系统可靠性分析[M].北京: 清华大学出版社, 2003.

[13]滕林, 刘万顺, 贠志皓, 等.电力系统暂态稳定实时紧急控制的研究[J].中国电机工程学报, 2003,23(1): 64-69.Tend Lin, Liu Wanshun, Yun Zhihao, et al.study of real-time power system transient stability emergency control[J].Proceedings of the CSEE, 2003, 23(1):64-69.

[14]薛禹胜.时空协调的大停电防御框架(1): 从孤立防线到综合防御[J].电力系统自动化, 2006, 30(1): 8-16.Xue Yusheng.Space-time cooperative framework for defending blackouts (partⅠ): From Isolated defense lines to coordinated defending[J].Automation of Electric Power Systems, 2006, 30(1): 8-16.

[15]Chen C K, Wei Y C A.An improved two-way partitioning algorithm with stable performance[J].IEEE Transactions on Computer-Aided Design, 1991,l0: 1502-1511.

[16]Parlett B N, Scott D S.The Lanczos algorithm with selective orthogonalization[J].Mathematics and Computations, 1979, 33(11): 217-238.

[17]Liu C C, Jung J, Heydt G T, et al.The strategic power infrastructure defense (SPID)system: a conceptual design[J].IEEE Control Systems Magzine, 2000,20(4): 40-52.