一种新型注入式混合有源电力滤波器

丁士启 帅智康 罗 安

（湖南大学电气与信息工程学院 长沙 410082）

1 引言

注入式混合型有源电力滤波器（Injection Type Hybrid Active Power Filter, IHAPF）兼顾谐波抑制和无功补偿功能，由于基波谐振支路的存在有效降低了有源部分的基波分压，是目前中高压电网谐波治理和无功补偿工程应用中采用较为广泛的形式。其核心在于采用注入支路实现基波电压有效分压，使有源滤波器基本不承受基波电压和基波电流，从而达到降低有源滤波器容量的目的[1-4]。

然而，在某些变电站及大型的工矿企业的中高压电网中，都配备相应的无功补偿装置，无功缺口不是很大，但是谐波治理装置却很少，谐波并没有得到有效治理，导致电网的电能质量降低，影响了企业的正常生产，甚至威胁电网的安全稳定运行[5-8]。如果采用注入式结构会出现两种情况:①注入电容满足无功补偿需要的情况下，电容取值会很小，谐波阻抗增大，谐波电流的注入能力受限；②注入电容满足谐波注入能力的情况下，电容值会比较大，无功会出现过补现象。同时，在实际的应用中，受基波串联谐振支路失谐及检测环节误差的影响，IHAPF的有源部分与基波谐振支路间会产生基波环流，严重时甚至烧毁逆变器。

因此，本文在研究IHAPF基波环流产生机理的基础上，提出了一种新型注入支路拓扑结构，保留了IHAPF的优点，在保证注入能力的同时，可满足任意容量的无功补偿要求，并在结构上抑制了基波环流的产生，避免了控制失效时事故的发生；建立了新型注入式混合有源电力滤波器（Novel Injection type Hybrid Active Power Filter, NIHAPF）的电气模型，以此为基础分析了NIHAPF的滤波原理及注入支路对滤波能力的影响，提供了注入支路参数设计依据；并从基波谐振支路谐波分压和串联谐振支路谐波分流两个方面探讨了新型结构的优越性；仿真及实验结果验证了本文理论分析的有效性。

2 IHAPF基波环流的产生机理

文献[9]从控制的角度，分析了当 IHAPF控制系统检测环节存在误差时，控制器给定信号中将存在基波成分，导致逆变器与基波谐振支路间产生很大的基波电流，威胁逆变器的安全；并提出IHAPF双闭环控制策略，提高了 IHAPF有源部分基波阻尼，有效地抑制了检测环节误差导致的基波环流，提高了系统的可靠性。但是，该文并未从主电路结构的角度分析基波环流的问题，尤其是当基波谐振支路失谐时，即使采用双闭环控制策略也难以抑制基波环流的产生。

本文将从结构上分析 IHAPF基波环流的产生机理。

图1 系统注入支路结构图Fig.1 System topology of the injection sub-circuit

如图1所示，在逆变器工作期间，任意时刻都有3个管子导通构成回路，从直流侧来看是电压型逆变器，输出的是与参考信号成比例的谐波值，没有基波量；当注入支路的参数确定时，注入支路的基波电流量基本恒定，相当于一个基波电流源。从注入支路来看它相当于一个电流型逆变器，对基波调制时相当于三个升压斩波电路，也就是常用的PWM整流电路，但是当调制谐波时，虽然还是PWM整流，可输出变得不确定，会产生很大的基波电流，流经输出电抗的基波量与系统取值有关。

理想情况下基波谐振支路完全调谐，并忽略基波谐振支路电感的内阻，基波谐振支路在基波频率下阻抗为零，即 Z2等于零。对于 IHAPF来说，基波谐振支路在基波频率时可以看成是短路，由于输出滤波器Lm的存在，系统电压作用于IHAPF注入支路时产生的基波电流完全由基波谐振支路承担，其有源逆变部分不承受基波电压和基波电流。

然而在工程应用中，受制造工艺的限制基波谐振支路参数会存在误差。因此，Z2在基波频率处的等效阻抗不为零。假设基波谐振支路偏感性，失谐率为α；基波谐振电感 L1的品质因数为 Q，则在基波频率处基波谐振支路的等效阻抗为

式中，ω为基波角频率。

则电网电压作用于IHAPF注入支路时，产生的流经有源部分的基波电流为

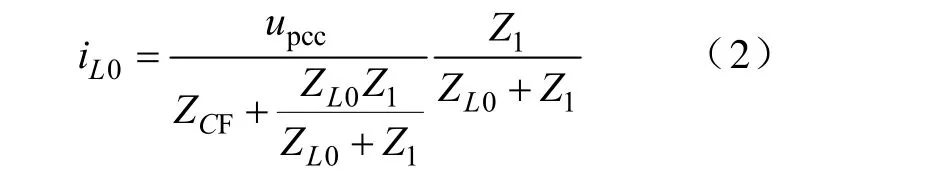
从上式可以看出，当基波谐振支路等效阻抗不为零时，将在IHAPF有源部分与基波谐振支路间形成基波环流。该基波电流的值与基波谐振支路的失谐度以及逆变器输出滤波电抗器的值有关，一般情况下，为确保逆变器的谐波输出性能，输出滤波电抗器取值不会太大，因此，基波环流会比较大，严重时会烧坏逆变器的开关管。

3 新型注入式混合型有源电力滤波器结构

为了提高 IHAPF基波串联谐振支路失谐时系统的可靠性，本文提出了新型注入式混合有源电力滤波器拓扑结构，NIHAPF的系统结构如图2所示。

图2中，US为电网电压，ZS为电网等效阻抗，L1、C1构成基波并联谐振，L2、C2构成基波串联谐振，C为直流侧电容，L0和C0构成输出滤波器，用于滤除逆变器输出的高频毛刺。NIHAPF系统的有源部分采用IPM模块构成电压型逆变器，其无源部分采用单调谐回路。

图2 新型注入式混合型有源滤波器的拓扑结构Fig.2 Topology of novel injection type hybrid APF

由图2可以看出，有源部分通过耦合变压器与由 L2、C2构成的串联谐振支路并联再与 L1、C1构成的并联谐振注入支路串连接入电网。在基波域L1和C1并联基波谐振对于有源部分相当于开路，在谐波域有源部分只承受 L2和 C2上分到的很小的谐波电压，从而有效降低有源部分IPM模块的容量，在很大程度上克服有源电力滤波器的容量限制，更易实现有源电力滤波器的大功率应用，并降低了系统成本。

此结构中，并联支路和串联支路组成了双重保护，当并联支路完全谐振时，并联谐振支路承受全部基波电压，串联支路中没有基波电流，有源部分也不会发生基波环流，当并联支路失谐时，仍可保证并联谐振支路承受几乎所有基波电压；基波电流仍然能够绝大多数流入串联谐振支路，从而在更大范围内保证有源滤波器不承受基波电压和电流。

综上所述，NIHAPF利用基波并联谐振构成了很大的基波阻抗，使基波电压完全施加在基波并联谐振电路上，从而使NIHAPF的有源部分仅承受谐波电压，不承受基波分量。NIHAPF的谐波电流注入部分由于构成了基波并联谐振，其注入支路不能进行无功补偿，因此，NIHAPF更加适用于功率因数高、谐波污染严重的冶炼企业，通过适当的调整基波并联谐振电路的取值，既可保证谐波电流的注入能力。在无功需求较大的场合，可以增加单调谐滤波器，实现大容量无功补偿和谐波动态治理。

4 NIHAPF的运行机理研究

4.1 NIHAPF的电气模型

对上述NIHAPF进行简化处理[10-14]:假设电网谐波电压为USh；电网谐波域等效阻抗为ZSh；非线性负载等效为谐波电流源ILh；有源部分被控制为一个理想的谐波电压源UI；则NIHAPF的谐波域单相电气模型如图3所示。

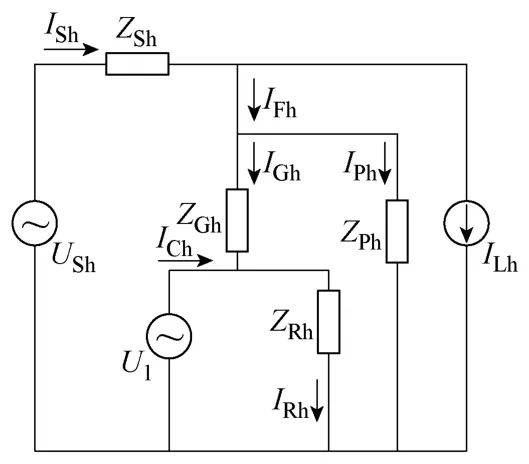
图3 系统单相等效电路图Fig.3 Single phase equivalent circuit

从式（4）可以看出，当控制放大倍数 K足够大时，流入电网的谐波电流将会很小，接近于 0，起到抑制谐波电流的作用；同时可以抑制无源部分与电网阻抗间的并联谐振。

4.2 新型IHAPF注入支路谐波分压分析

基波串联谐振支路谐波分压不仅对有源部分的器件选型有直接影响，还有可能在基波串联谐振支路分压大于直流侧电压的情况下，通过 IGBT续流二极管向直流侧反向充电，抬升直流侧电压，对系统稳定造成影响。基波串联谐振支路的谐波分压主要来源于两个方面，一方面是电网谐波电压在基波谐振支路的分压，另外一个重要的方面是由于基波环流分压和注入支路调谐频率附近的谐波电压被严重放大，造成基波串联谐振支路谐波含量急剧增加。基波串联谐振支路谐波分压大时严重影响有源电力滤波系统的整体性能，甚至造成开关管因过流而烧毁的现象。在传统的IHAPF结构中，通过提高注入支路的谐振频率理论上可以降低基波谐振支路的谐波分压，但是，这是以牺牲APF的谐波注入能力为代价的[15]。在实际的运行过程当中，由于电网中含有较高频率的谐波电压，即使提高了注入支路的谐振频率仍然存在谐波放大的现象。

为研究NIHAPF注入支路的基波并联和基波串联支路的谐波分压情况，本节建立了NIHAPF注入支路的谐波分析等效电路，如图4所示。

图4 并联和串联基波谐振支路谐波分压等效电路Fig.4 fundamental resonant sub-circuit of the parallel and series

由图4可知，当谐波次数为n次时，可得到基波并联支路和串联支路的阻抗分别为

基波并联和串联谐振支路的电压分压比和电流分流比分别为

在基波域，当 n=1时，ku=∞，ki=0即 Z2并联谐振承受所有基波电压，串联谐振不承受基波电压。图5为利用Matlab仿真软件对本文提出的新型结构NIHAPF支路的仿真结果，对注入并联基波谐振支路的阻抗和串联基波谐振支路的分压和分流特性进行了频谱分析。仿真参数见表1。

图5 NIHAPF结构阻抗特性仿真图Fig.5 Simulation results of impedance characteristic

表1 仿真参数Tab.1 Parameters of simulation

从图5中可以看出在谐波域，当f ＞300Hz时，ku＜1即串联谐振支路的谐波电压就开始大于并联支路，随着n的增大，ku会越来越小，谐波电压大部分会加到串联谐振支路；另外，当f =50Hz时，即基波频率处，基波并联谐振支路的分压远远大于基波串联谐振的分压，即使存在一定的失谐，基波并联谐振支路仍将承受几乎所有的基波电压，从而从结构上避免了基波环流的产生。

表2为利用实验室HAPF开发平台获得的两种结构的基波谐振支路各次谐波电压的幅值，采用传统注入式结构时通过改变注入电容的值分别谐振在3.8次和10次，系统参数如表1所示。滤波系统由实验室 380V三相交流电源供电，其中谐波电压主要为3、5、7次，幅值分别为4V、2V和1V。

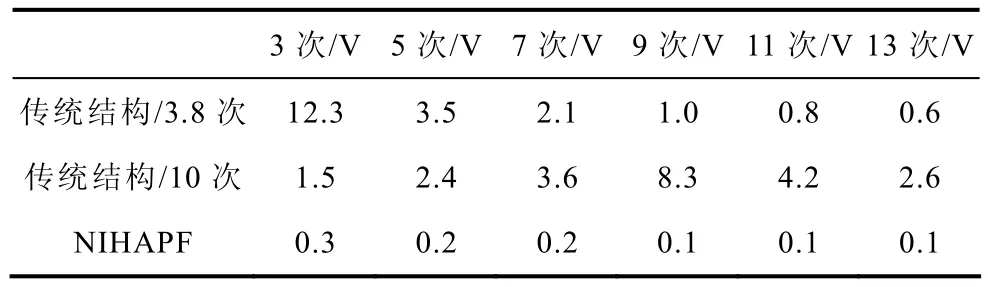
表2 基波谐振支路谐波分压实验结果Tab.2 Experimental results of harmonic voltage supported by fundamental circuits of different topologies

传统的注入式结构由于谐波电流注入部分为一个电容，随着频率的升高其等效阻抗逐渐降低，电网中的谐波电压几乎全部降在了基波谐振支路上。并且由于注入电容的取值不能无限制的增大，在低频段整条注入支路的谐振点处存在谐波电压放大的现象，大大增大了基波谐振支路承受的谐波电压值。而本文提出的NIHAPF新型结构，谐波注入部分为一并联基波谐振支路，由于电感的存在，提高了注入电容值，降低了基波谐振支路的谐波分压值，还可以避免电网低频谐波电压的放大现象。

由表2可以看出，通过减小注入电容的取值，提高注入支路的谐振频率可以在一定程度上降低基波谐振支路的谐波分压，但是仍然存在严重的谐波放大现象。而NIHAPF的注入支路基本不会发生谐振的情况，因此很好地避免了谐波放大现象，而且还不会产生基波环流，大大降低了基波谐振支路的谐波分压。

4.3 并联基波谐振注入支路谐波分流分析

由图5的频谱图可以看出，由于NIHAPF新型结构中的谐波电流注入部分谐振在基波，可以根据实际情况增大注入电容值也不会发生无功过补的情况，对于有源部分发出的谐波电流随着发出谐波频率的增大，串联基波谐振支路的分流会越来越小。由于APF主要补偿5次及以上的高次谐波，在APF输出谐波电压有限的情况下，能够获得很好的谐波电流注入效果。注入支路串联谐振次数为m时，注入电容对于n次谐波的阻抗为[15]

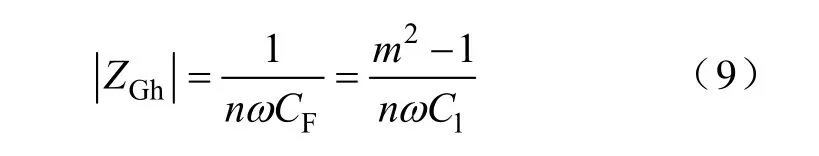
新型注入结构的注入支路的阻抗为

根据式（9）和式 10）可以看出，传统注入支路阻抗与m2成正比，随着谐振次数m的增加，|ZGh|的值急剧增大，严重限制了谐波电流的注入能力；新型结构注入支路由于结构特性不会出现低次谐振点，|ZGh|的值只与发出的谐波次数有关，通过增大注入电容值就可以提高谐波电流的注入能力。

5 仿真与实验结果

为验证NIHAPF结构在基波环流抑制方面的有效性，分别对传统IHAPF和新型NIHAPF进行了仿真验证。负载参数根据某铜冶炼企业 10kV母线实测数据，利用理想电流源模拟。其中，三相电源电压为10kV，频率为50Hz；5次、7次、11次和13次谐波电流分别为35.8A、40.9A、45.3A和20.5A。

仿真采用开环仿真和闭环仿真两种形式，第一组仿真开环控制信号中不包含基波分量，只考虑基波串联谐振支路失谐的影响；第二组仿真采用闭环控制，同时考虑基波串联谐振支路失谐和检测误差导致控制给定信号存在基波分量的形式，闭环控制采用文献[9]所述的双闭环控制策略。

系统主电路参数如表3所示。传统IHAPF的注入电容的取值根据电网所需补偿的无功功率计算获得；同时，兼顾谐波电流注入比和基波串联谐振支路的谐波分压，基波串联谐振支路电容和电感参数分别为 690μF和 14.7mH，具体设计方法见参考文献[15]。为确保 IHAPF和 NIHAPF的可比性，NIHAPF的主电路参数与 IHAPF一致，因此，NIHAPF基波并联谐振支路的电感值为

表3 系统参数Tab.3 Parameters of system

开环控制仿真结果如图6和图7所示。

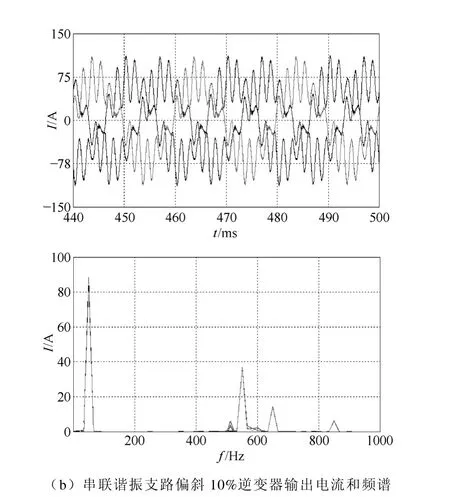
图6 开环传统注入式结构逆变器输出电流Fig.6 Inverter output current and spectrum of the traditional IHAPF with open-loop

图7 开环新型注入式结构逆变器输出电流和频谱Fig.7 Inverter output current and spectrum of the NIHAPF with open-loop

从图 6a、图 6b两个图对比可以得出，开环控制时，当基波串联谐振支路参数变化时，对于相同的谐波参考量，逆变器输出的基波电流不同，从而直观的说明了基波环流产生的原因。由图7可以看出，开环控制时，对于相同的谐波参考量和系统参数，NIHAPF系统中的逆变器的输出只有控制所导致的很少的一部分基波量，改变注入支路的参数对基波量输出没有影响；而治理效果取决于注入电流的大小，相同注入电容值时，新型结构的注入效果要好。

闭环控制仿真结果如图8和图9所示。

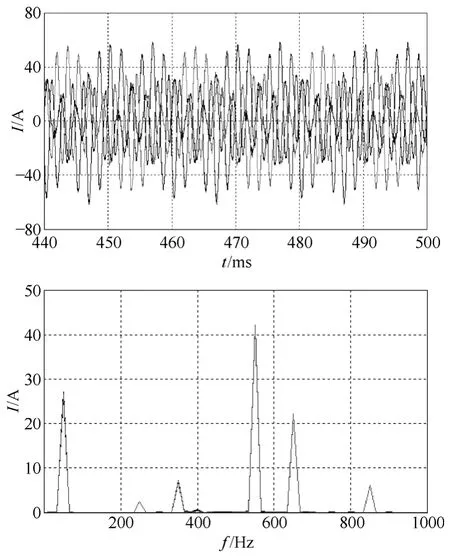
图8 双闭环注入式结构逆变器输出电流和频谱Fig.8 Inverter output current and spectrum of the traditional IHAPE structure with dual close loop control

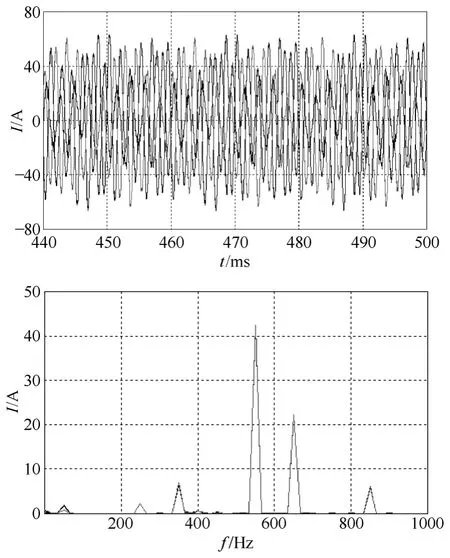
图9 闭环新型注入式结构逆变器输出电流和频谱Fig.9 Inverter output current and spectrum of the NIHAPF with close loop control

对比图8和图9也可以看出，闭环控制的时候，新型的注入式结构也不会产生基波分量，而传统的注入式结构除了由于检测，控制等导致的误差原因，还有逆变侧的基波分流，控制器输出一个基波频率的信号，而这个信号由于传递函数在基波频率处很高的增益，将会产生很大的输出电流，而这个电流信号又无法被输出电流检测到，无法进行控制，这等于处于一种失控状态。这样的系统是很不稳定的，难以可靠运行。而且，由于无法对逆变器的输出电流控制，通常会因逆变器过流而烧毁功率器件。新型结构则完全避免了这种情况的发生。

为了进一步验证本文提出的NIHAPF结构的有效性，搭建了传统 IHAPF和本文提出的新型NIHAPF实验平台，实验平台利用380V系统模拟不同结构对基波环流的抑制情况。

由图10和图11可以看出，传统的IHAPF在基波串联谐振支路失谐时，会在逆变器输出中引起基波分量；而NIHAPF结构中几乎不含有基波分量，从而验证本文理论分析的有效性。

图10 传统注入式结构逆变器输出电流和频谱图Fig.10 Inverter output current and spectrum of the traditional structure

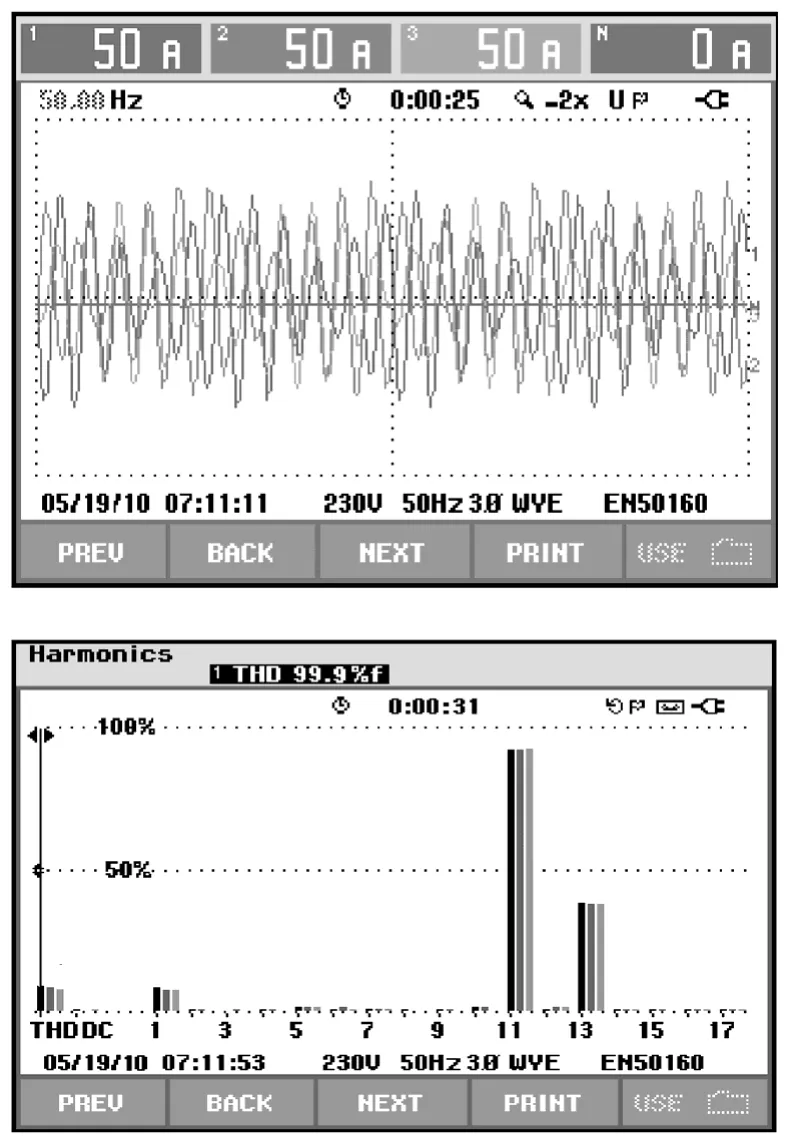
图11 新型注入式结构逆变器输出电流和频谱图Fig.11 Inverter output current and spectrum of the novel structure

6 结论

本文针对传统注入式混合有源电力滤波设备在实际工程应用中存在的问题和缺陷进行分析，从理论上分析了注入支路基波环流产生的机理，并提出了一种新型注入式混合型有源电力滤波器来解决注入支路基波环流问题，最后通过仿真实验和物理模拟实验对其性能进行了验证，实验结果表明了该新型结构的有效性和实用性。

[1]IEEE recommended practices and requirements for harmonic control in electrical power system[S].IEEE,1993.

[2]王兆安, 杨君, 刘进军.谐波抑制与无功补偿[M].北京:机械工业出版社, 1998.

[3]陈国柱, 吕征宇, 钱照明.有源电力滤波器的一般原理及应用[J].中国电机工程学报, 2000, 20 (9):17-21.Chen Guozhu, Lü Zhengyu, Qian Zhaoming.The general principle of active filter and its application[J].Proceedings of the CSEE, 2000, 20 (9): 17-21.

[4]罗安, 付青, 王丽娜, 等.变电站谐波抑制与无功补偿的大功率混合型电力滤波器[J].中国电机工程学报, 2004, 24(9): 115-123.Luo An, Fu Qing, Wang Lina, et al .High-capacity hybrid power filter for harmonic suppression and reactive power compensation in the power substation[J].Proceedings of the CSEE , 2004, 24(9):115-123.

[5]唐卓尧, 任震.并联型混合滤波器及其滤波特性分析[J].中国电机工程学报, 2000, 20(5): 25-29.Tang Zhuoyao, Ren Zhen.Hybrid filter connected in series APF with PF and compensating characteristic analysis[J].Proceedings of the CSEE, 2000, 20(5):25-29.

[6]汤赐, 罗安, 范瑞祥, 等.新型注入式混合有源滤波器应用中的问题[J].中国电机工程学报, 2008,28(18): 47-53.Tang Ci, Luo An, Fan Ruixiang, et al.Problems in application of new injection type hybrid ative power filter[J].Proceedings of the CSEE, 2008, 28(18):47-53.

[7]罗安, 章兢, 付青.新型注入式并联混合型有源电力滤波器[J].电工技术学报, 2005, 20(2): 51-55.Luo An, Zhang Jing, Fu Qing.Development of high-capacity hybrid active power filter[J].Transactions of China Electrotechnical Society, 2005,20(2): 51-55.

[8]孙佐, 王念春, 许卫兵.一种高性价比并联混合有源电力滤波器[J].中国电机工程学报, 2007, 27(36):79-84.Sun Zuo, Wang Nianchun, Xu Weibing.A parallel hybrid active power filter with good cost performance[J].Proceedings of the CSEE, 2007,27(36): 79-84.

[9]孙贤大, 罗安, 帅智康, 等注入式混合型有源电力滤波器双闭环控制[J].电工技术学报, 2009, 24(9):127-133.Sun Xianda, Luo An, Shuai Zhikang, et al.Dual-loop control strategy of hybrid active power filter with injection circuit[J].Transactions of China Electrotechnical Society, 2009, 24(9): 127-133.

[10]郭伟峰, 武健, 徐殿国, 等.新型滑模控制的并联混合有源电力滤波器[J].中国电机工程学报, 2009,29(27): 29-35.Guo Weifeng, Wu Jian, Xu Dianguo, et al.Hybrid shunt active power filter based on novel sliding mode control[J].Proceedings of the CSEE, 2009, 29(27):29-35.

[11]唐欣, 曾启明, 陈伟乐.有源电力滤波器的双闭环串级控制[J].中国电机工程学报, 2008, 28(24):29-35.Tang Xin, Tsang K M, Chan W L.Double closed-loop cascade control for active Power filter[J].Proceedings of the CSEE, 2008, 28(24): 29-35.

[12]涂春鸣, 盘宏斌, 帅智康, 等.谐振阻抗型混合有源滤波器输出电流相移的分频预估补偿[J].电工技术学报, 2008, 23(10): 114-120.Tu Chunming, Pan Hongbin, Shuai Zhikang, et al.Predictive compensation at different frequency for current phase dalay of resonant impedance type hybrid active filter[J].Transactions of China Electrotechnical Society, 2008, 23(10): 114-120.

[13]唐欣, 罗安, 涂春鸣.新型注入式混合有源滤波器的研究[J].电工技术学报, 2004, 19 (11): 50-55, 60.Tang Xin, Luo An, Tu Chunming.Study of new injection type hybrid active power filter [J].Transactions of China Electrotechnical Society, 2004,19(11): 50-55, 60.

[14]杨进, 杨向宇, 余辉.基于逆变器多重化的串联混合型有源滤波器的仿真研究[J].电工技术学报,2004, 19(10): 23-26.Yang Jin, Yang Xiangyu, Yu Hui.The simulation of serial hybrid active power filter based on multiplicity of inverter[J].Transactions of China Electrotechnical Society, 2004, 19(10): 23-26.

[15]帅智康, 罗安, 范瑞祥, 等.注入式混合有源电力滤波器的注入支路设计[J].电力系统自动化, 2007,31(5): 1-5.Shuai Zhikang, Luo An, Fan Ruixiang, et al.Injection branch design of injection type hybrid active power filter[J].Automation of Electric Power Systems, 2007,31(5): 1-5.