基于波形时域分布特征的变压器励磁涌流识别

王 雪 王增平

（华北电力大学电力工程系 保定 071003）

1 引言

差动保护仍是当前广为应用的变压器主保护，随着大容量变压器的投入运行，变压器差动保护的快速性和可靠性面临更加严峻的考验，如何区分励磁涌流和故障电流仍是变压器差动保护的重要研究课题之一。工程中主要应用二次谐波制动判据、间断角判据、波形对称判据来防止励磁涌流造成差动保护误动[1-2]，但是由于大容量变压器铁心材料的改进以及系统中无功补偿装置的应用使得涌流和故障暂态电流中二次谐波含量的差别减小，二次谐波制动判据不正确动作的可能性提高了，波形对称判据和间断角判据都是依据励磁涌流波形发生畸变并有间断的特征，但铁心极度饱和或产生对称性涌流时，上述原理的保护都有可能误动。近年来众多学者提出很多新方法，总体可分为两类:一类是继续探究电流波形特征并利用不同的技术手段加以提取[3-6]；另一类是引入电压量，构成诸如基于差有功[7]、磁通特性[8]或等效瞬时励磁电感[9-10]的励磁涌流识别方法，或者构成不依赖于差动保护的新型主保护原理，如基于等效瞬时漏感[11]或回路方程[12]的新型保护。这些新型主保护在理论上完全不受励磁涌流的影响，具有很好的研究前景，但是由于引入电压量必须考虑电压互感器的暂态响应特性，且电压互感器二次断线时必须退出运行，此时只能依赖电流差动保护。因此研究仅依赖电流特征的励磁涌流识别方法仍具有十分重要的意义。

当变压器铁心饱和时，励磁涌流波形将出现严重的畸变，而故障电流基本符合正弦波的特征，二者波形的时域分布特征存在明显的差异。本文根据励磁涌流生成的机理，分析了励磁涌流和故障电流波形的时域分布特征，并给出了相应的励磁涌流识别判据。动模实验和数字仿真结果均表明该方法具有原理简单、便于实现、灵敏度高等特点，性能上优于二次谐波制动原理和间断角原理。

2 基本原理

2.1 励磁涌流波形的时域分布特征

图1给出了用直线近似表示的铁心磁化曲线，图中Φs为铁心的饱和磁通。当铁心磁通φ ＜Φs时励磁电流为零，等值励磁阻抗为无穷大，φ ＞Φs时铁心饱和，产生很大的励磁电流，等值励磁阻抗大大减小(为常数)。

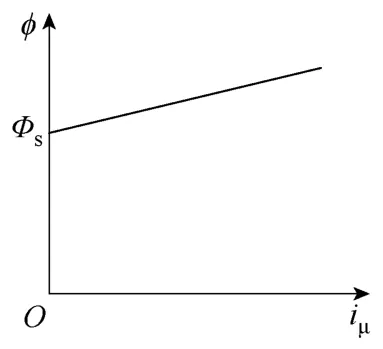
图1 变压器铁心磁化曲线Fig.1 The magnetization curve of transformer core

以单相变压器为例加以分析，设空载合闸时电源电压为

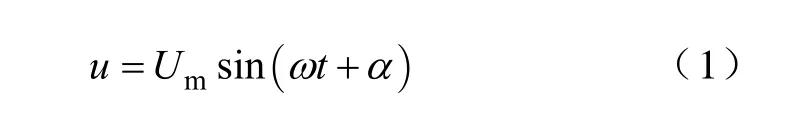
式中，α为合闸初相角。

设变压器铁心剩磁为Φr，额定工作磁通为Φm，在简化的铁心磁化特性下可得励磁涌流为[13]

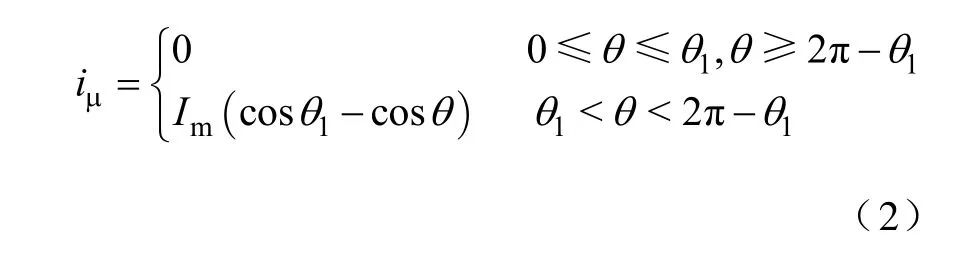
式中，θ =ωt+α；θ1=arccos（cosα+kr-ks）；kr=Φr/Φm；ks=Φs/Φm。

令α=0、kr=0.8、ks=1.1，将各参数代入式（2）可得励磁涌流波形如图2a中实线所示，很明显励磁涌流波形不再满足正弦波特征，且偏向时间轴一侧。

直方图技术是数字图像处理中的一种常用方法，它能提供非常有用的图像信息统计资料。对于某个灰度图像，假设其灰度级为[0，L]，图像总像素个数为 n，定义灰度直方图为离散函数 h(r)=nr，其中 r表示某个灰度级(0≤r≤L)，nr表示图像中灰度级为r的像素个数[14]。借鉴直方图处理技术来描述励磁涌流波形分布特征，首先以一个工频周期内差动电流瞬时值的最大绝对值为基准对差电流进行归一化处理，归一化后的电流最大取值范围为[-1，1]，将该取值区间等分为2N个子区间，各子区间标号分别记为-N, ··, -1，1, ··, N，每个区间的长度为1/N。分别统计一个工频周期内电流瞬时值位于每个子区间的采样点数目，假设位于第n个子区间的采样点数目为mn，定义第n个子区间的分布系数为

式中，M为一个工频周期的采样点总数；n∈[-N，N]。

取N=10，纵向划分涌流波形，如图2a中网格线所示，计算每个区间的分布系数。将区间标号作为横坐标，分布系数作为纵坐标，可得励磁涌流波形分布系数直方图，如图2b所示。可见由于波形存在间断部分，且偏向正半轴，因此标号为负的子区间的分布系数为零，第1区间分布系数最大，而第10区间分布系数相对要小。实际变压器铁心进入和退出饱和阶段，励磁涌流波形呈凹弧特性和明显的尖顶波特性，如图2a中虚线所示。显然此时第1、10子区间的分布系数差异更大。

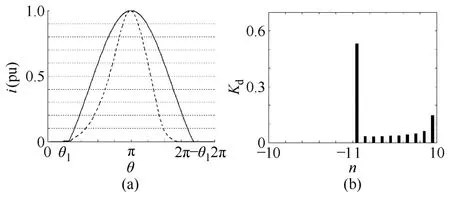
图2 不对称励磁涌流及波形分布系数直方图Fig.2 Asymmetric inrush current waveform and its distribution coefficient histogram

对于 Yd联结三相变压器，由于不能得到三角形侧的绕组电流，实际上差动电流为两相电流之差，此时往往有一相差动电流波形呈现对称性。当两相的暂态磁通相同时，可能出现正负峰值相等的对称性励磁涌流，如图3a所示，此时的波形分布系数直方图如图3b所示。与不对称涌流的情况相比，此时直方图呈对称分布，但仍具有第1区间分布系数最大，而第±10区间分布系数相对要小的特点。

图3 对称性励磁涌流及波形分布系数直方图Fig.3 Symmetric inrush current waveform and its distribution coefficient histogram

2.2 故障电流波形的时域分布特征

不计变压器绕组电阻时，基于等效瞬时电感的变压器模型满足如下方程[10]:

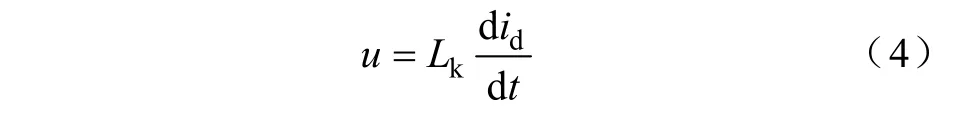
式中，u为绕组端电压；id为差电流；Lk为等效瞬时电感。

由式（4）可知，故障电流的波形变化特征由绕组端电压和等效瞬时电感决定。端电压仅在故障发生时刻发生突变，之后即保持不变。由于变压器内部故障时铁心不会饱和，其励磁电感和各绕组漏感均可假定为常数，因此等效瞬时电感为常数，故障差电流也基本保持工频正弦特性。图4a给出了一个工频周期正弦特性的故障电流波形，此时的波形分布系数直方图如图 4b所示。可见直方图呈对称分布，与励磁涌流情况不同的是第±1区间分布系数最小，而第±10区间分布系数最大。

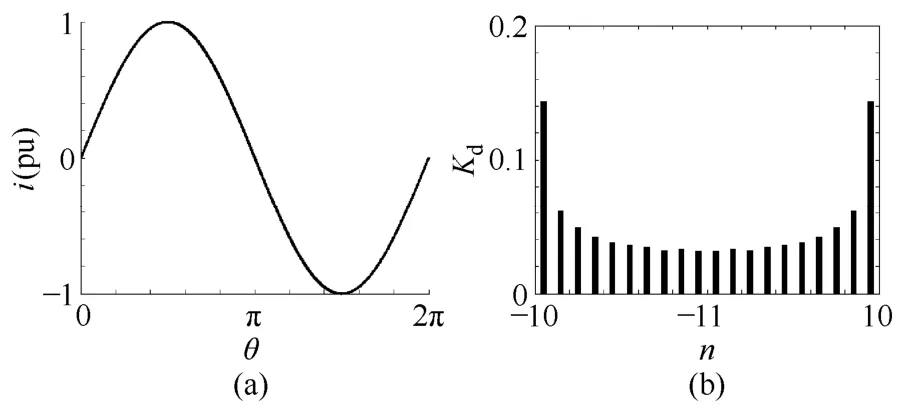
图4 故障电流及波形分布系数直方图Fig.4 Fault current waveform and its distribution coefficient histogram

实际上在各子区间内电流基本上是单调变化的，变化率越大，则处于该子区间内的采样点数就越少，因此根据式（3）的定义可知各子区间的分布系数反比于该区间内电流的变化率。对于励磁涌流，无论非对称涌流还是对称性涌流，第±1区间内电流波形处于间断部分，电流变化率小，采样点多，因而分布系数大，而在第±N区间内波形为尖顶波，电流变化率大，采样点少，因而分布系数小；对于故障电流，第±1区间内电流处于过零点附近，电流变化率大，采样点少，分布系数小，在第±N区间内波形处于峰值附近，电流变化率相对要小，采样点较多，分布系数相对比较大。这和前面的计算结果是完全吻合的。

2.3 保护方案的设计

为了描述励磁涌流和故障电流的各子区间分布系数的差异，本文定义电流波形分布特征系数D如下:

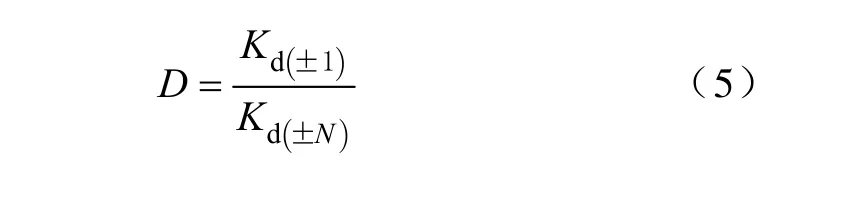
式中，Kd(±1)和 Kd(±N)分别为第±1和±N 子区间的波形分布系数。

显然，故障电流的分布特征系数较小，而励磁涌流的分布特征系数要大得多。

综合上述分析，本文提出如下的保护方案:

（1）差电流归一化。以一个工频周期内差动电流瞬时值的最大绝对值为基准对其进行归一化处理。

（2）分别计算第±1、±N子区间的电流波形分布系数 Kd(±1)和 Kd(±N)。

（3）计算波形分布特征系数。当D≥Dset时，判断为励磁涌流闭锁差动保护；当 D＜Dset时，判断为内部故障开放差动保护跳闸。Dset为判据的门槛值。

要计算波形分布特征系数，首先需要确定划分的子区间数目。对于固定的电流波形，如果子区间数目不同，则每个子区间内采样点的数目也会不同，波形分布特征系数也将随之变化。对于图 2、图 4给出的简化条件下的励磁涌流和故障电流波形，波形分布特征系数可由下面公式分别计算

从式（6）可知励磁涌流的分布特征系数还与合闸时的状态有关，励磁涌流越严重波形分布特征系数越小。众所周知当电压瞬时值过零时刻合闸同时剩磁越大、饱和磁通越小，产生的励磁涌流越严重，本文考虑比较极端的情况，取α=0，kr=1.0，ks=1.1。确定变压器合闸状态参数后，波形分布特征系数的大小就仅与子区间的数目有关。式(6)、式(7)描述的二者之间关系如图5所示。

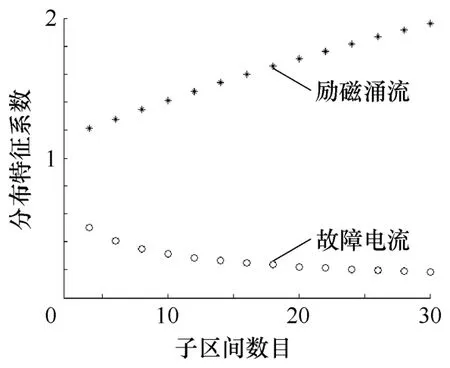
图5 分布特征系数与子区间数目关系示意图Fig.5 Relationship between the distribution characteristic coefficient and the numbers of subintervals

从图5可以看到随着子区间数目的增加，励磁涌流波形分布特征系数随之变大，故障电流波形分布特征系数随之变小，主要是因为对于励磁涌流，随着子区间数目的增加，第±N子区间分布系数显然会减小，而由于波形间断部分采样点始终处于第±1子区间内，因而第±1子区间分布系数减小较少，所以励磁涌流的波形分布特征系数会变大。而对于故障电流，第±N子区间分布系数比第±1子区间分布系数要大得多，因此随着子区间数目的增加第±N子区间分布系数相对减小较少，而第±1子区间分布系数相对减小较大，因而故障电流的分布特征系数会变小。因此从增大励磁涌流和故障电流差异角度来看，可以划分较多的子区间。另一方面，由于实际上励磁涌流在变压器铁心不饱和阶段并非完全等于零，如果子区间过多，则第±1子区间分布系数可能减小更多，那么其波形分布特征系数反而会减小。本文综合考虑这两方面的因素，取N=10。

3 方法验证

为了分析提出的新型变压器励磁涌流识别判据的性能，本文分别利用大量动模实验和数字仿真数据[15]对其进行了验证。

3.1 动模实验及数字仿真系统简介

动模实验系统如图6所示，其中实验变压器由三个单相变压器组成，采用 Yd11联结。单相变压器参数如下:额定容量为10kVA，低压侧额定电压为 380V，额定电流为 25.3A，高压侧额定电压为1kV，额定电流为10A，空载电流为1.45%×25.3A，空载损耗为 1%×10kVA，短路损耗为 0.35%×10kVA，短路电压为（9.0～15.0）%×1kVA，高压侧线圈288匝，由于系统电压的原因实验中仅接入78匝，低压侧线圈112匝，全部接入。

图6 变压器实验系统图Fig.6 Transformer experimental system

动模实验的内容包括:正常变压器空载合闸、内部故障变压器空载合闸、运行中变压器发生内部故障等工况。

由于动模实验中不能控制变压器铁心剩磁以及合闸初相角，难以获得最严重的励磁涌流的情况，同时故障位置也不能任意设置，因此动模实验数据具有一定的局限性。作为动模实验的重要补充，本文同时进行了数字仿真，仿真中可任意设置与运行工况有关的各参数，可使结果更全面。数字仿真中变压器参数与实验变压器参数相同。

3.2 分析结果

图7给出了变压器正常空投时的励磁涌流。图7a、7c分别为偏向负轴和对称性励磁涌流，各自的波形分布系数直方图分别为图7b、7d，显然和前面的理论分析结果是相符合的。按式（5）计算得到波形分布特征系数分别为7.1和7.6。

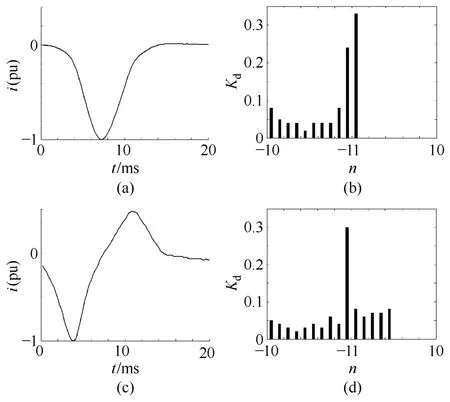
图7 动模实验中励磁涌流及波形分布特征直方图Fig.7 Inrush currents obtained by dynamic experiment and its waveform distribution coefficient histogram

图8给出了变压器发生B相匝间故障时差电流的波形，其中图8a、8c分别为带故障变压器空载合闸和变压器运行中发生故障的情况。从图8a可以看到空载合闸于故障变压器时差电流还带有明显的涌流特征，如前5ms内的波形呈尖顶波特点，在之后的一段时间内铁心退出饱和故障电流的特征才呈现出来，图8b为此时的波形分布系数直方图，基本符合故障的特点，与前面涌流时的结果有明显的区别。图8c中的故障电流基本符合正弦特征，其波形分布直方图也与前面理论分析结果十分符合。按式（5）计算得到波形分布特征系数分别为1.0和0.23。

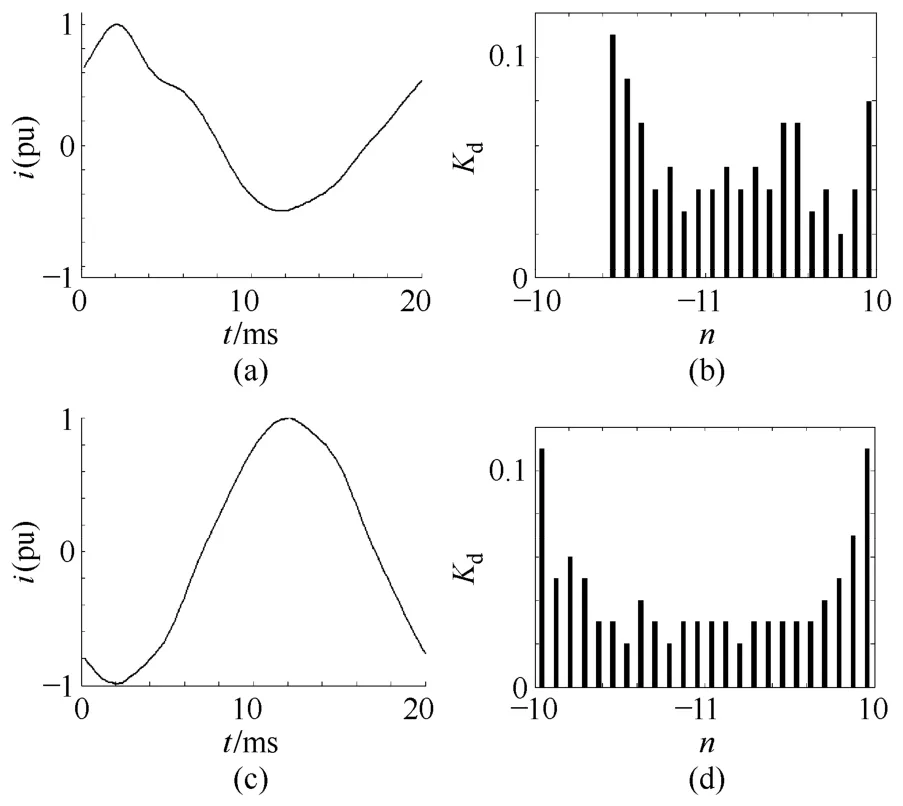
图8 动模实验中匝间故障电流及波形分布特征直方图Fig.8 Turn-to-turn fault currents obtained by dynamic experimental and its waveform distribution coefficient histogram

表1给出了不同运行状态下实验变压器差电流波形分布特征系数的计算结果。每个运行状态下的结果均为多次实验结果的取值范围。从表1可得到，正常变压器空投时波形分布特征系数最小值为2.5，带故障变压器空投时该系数最大值为1.38，而变压器正常运行中发生故障时该系数最大值仅有0.91，励磁涌流和故障电流的波形分布特征系数具有较大差异。本文取 Dset=2，即可可靠区分励磁涌流和故障电统。

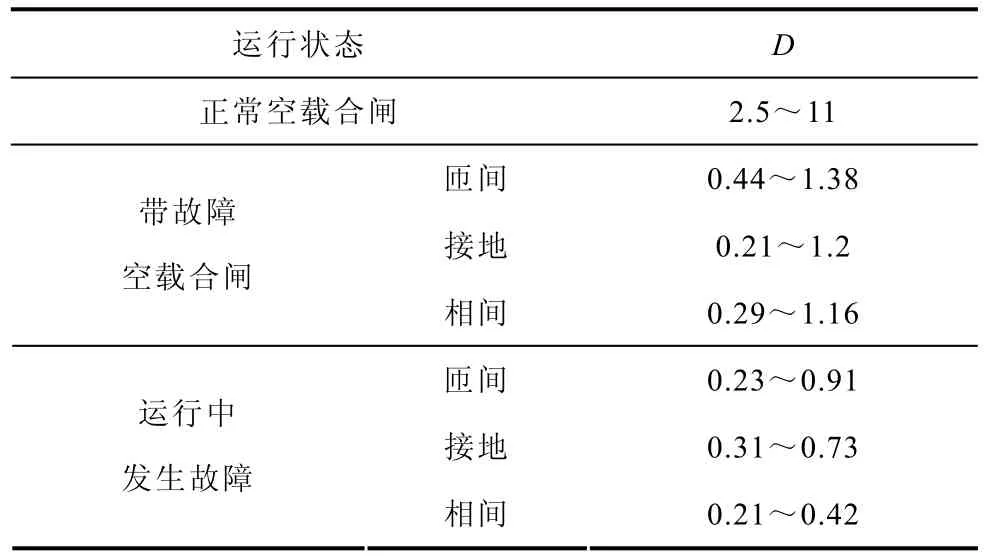
表1 实验数据的波形分布特征系数计算结果Tab.1 Experimental results of the waveform distribution characteristics coefficient of the differential current waveforms

表2给出了仿真数据的波形分布特征系数、二次谐波含量以及间断角的计算结果。对于正常空载合闸的情况统计各相的结果，对于变压器发生故障的情况只统计故障相计算结果中的最小值，其中对于间断角判据不统计空投时间断角较小但同时波宽小于140°可判断为涌流的情况。

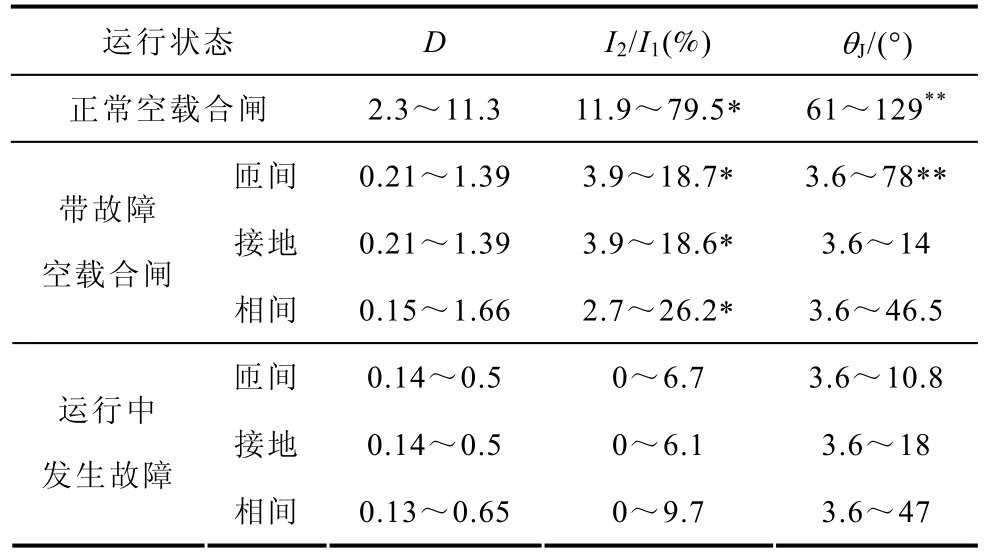
表2 仿真数据的波形分布特征系数（D）、二次谐波含量（I2/I1）和间断角（θJ）的计算结果Tab.2 Simulation results of waveform distribution characteristics coefficient, second harmonic content and the dead angle

从表2可以看到，仿真数据的波形分布特征系数范围与实验数据的结果相符，定值取2时可完全区分励磁涌流和故障电流。对于二次谐波制动判据如果定值取15%，对于部分情况包括正常空载合闸和变压器带轻微故障空载合闸(表2中用“*”标出)，保护会误动或延时动作。对于间断角判据，如果定值取 65°，则表 2中标“**”的情况同样存在误动或延时动作的可能。

从上面对比情况可知，波形分布特征判据在性能上优于现场普遍采用的二次谐波判据和间断角判据。主要在于二次谐波判据只能反应波形一个周期的总体特征，间断角判据仅反应铁心不饱和时波形出现间断的局部特点，而波形分布特征判据综合考虑铁心不饱和时波形出现间断以及铁心饱和时波形呈尖顶波的特征，可以更全面地反应涌流和故障电流之间的差异，因此性能得以提高。

4 结论

本文利用直方图技术分析了变压器励磁涌流和内部故障状态下差动电流波形时域分布特征，在此基础上提出一种基于波形分布特征的新型励磁涌流识别方法，并给出了具体的实现方案。该方法可以综合考虑变压器差电流在时域上的局部分布特征，更好地反应了励磁涌流和故障电流之间的差异。实验数据和仿真数据分析结果表明本方法具有更高的可靠性和灵敏度，性能优于二次谐波判据和间断角判据。

[1]孙志杰, 陈云仑.波形对称原理的变压器差动保护[J].电力系统自动化, 1996, 20(4): 42-46.Sun Zhijie, Chen Yunlun.Transformer differential protection based on the characteristic analysis of the first and second half cycle of the magnetizing inrush current [J].Automation of Electric Power Systems,1996, 20(4): 42-46.

[2]林湘宁, 刘世明, 杨春明, 等.几种波形对称法变压器差动保护原理的比较研究[J].电工技术学报,2001, 16(4): 44-49.Lin Xiangning, Liu Shiming, Yang Chunming, et al.Study on comparisons among some waveform symmetry principle based transformer differential protection[J].Transactions of China Electrotechnical Society, 2001, 16(4): 44-49.

[3]陈德树, 尹项根, 张哲, 等.虚拟三次谐波制动式变压器差动保护[J].中国电机工程学报, 2001,21(8): 19-23.Chen Deshu, Yin Xianggen, Zhang Zhe, et al.Virtual third harmonic restrained transformer differential protection principle and practice[J].Proceedings of the CSEE, 2001, 21(8): 19-23.

[4]郑涛, 刘万顺, 肖仕武, 等.一种基于数学形态学提取电流波形特征的变压器保护新原理[J].中国电机工程学报, 2004, 24(7): 18-24.Zheng Tao, Liu Wanshun, Xiao Shiwu, et al.A new algorithm based on the mathematical morphology for power transformer protection[J].Proceedings of the CSEE, 2004, 24(7): 18-24.

[5]焦邵华, 刘万顺, 刘建飞, 等.用小波理论区分变压器的励磁涌流和短路电流的新原理[J].中国电机工程学报, 1999, 19(7): 1-5.Jiao Shaohua, Liu Wanshun, Liu Jianfei, et al.A new principle of discrimination between inrush current and fault current of transformer based on wavelet [J].Proceedings of the CSEE, 1999, 19(7): 1-5.

[6]马静, 王增平, 徐岩.用相关函数原理识别变压器励磁涌流和短路电流的新方法[J].电网技术, 2005,29(6): 78-81.Ma Jing, Wang Zengping, Xu Yan.A novel method to identify inrush current and short circuit current based on correlation function[J].Power System Technology,2005, 29(6): 78-81.

[7]Yabe K.Power differential method for discrimination between fault and magnetizing inrush current in transformer[J].IEEE Transactions on Power Delivery,1997, 12(3): 1109-1118.

[8]孙志杰, 曾献华, 汤汉松.磁通制动原理在变压器差动保护中的应用[J].电力自动化设备, 2005,25(1): 79-81.Sun Zhijie, Zeng Xianhua, Tang Hansong.Application of flux restraint theory in transformer differential protection[J].Electric Power Automation Equipment, 2005, 25(1): 79-81.

[9]徐岩, 王增平, 杨奇逊, 等.基于电压电流微分波形特性的变压器保护新原理的研究[J].中国电机工程学报, 2004, 24(2): 61-65.Xu Yan, Wang Zengping, Yang Qixun, et al.Research on novel transformer protection based on the characteristics of voltage and differential current[J].Proceedings of the CSEE, 2004, 24(2): 61-65.

[10]葛宝明, 于学海, 王祥珩, 等.基于等效瞬时电感判别变压器励磁涌流的新方法[J].电力系统自动化,2004, 28(7): 44-48.Ge Baoming, Yu Xuehai, Wang Xiangheng, et al.A novel equivalent instantaneous inductance based algorithm used to distinguish inrush currents for transformers[J].Automation of Electric Power Systems, 2004, 28(7): 44-48.

[11]马静, 王增平, 王雪.基于等效瞬时漏感的变压器保护新原理[J].电力系统自动化, 2006, 30(23):64-68.Ma Jing, Wang Zengping, Wang Xue.Novel principle of power transformer protection based on equivalent instantaneous leakage inductance[J].Automation of Electric Power Systems, 2006, 30(23): 64-68.

[12]王增平, 徐岩, 王雪, 等.基于变压器模型的新型变压器保护原理的研究[J].中国电机工程学报,2003, 23(12): 54-58.Wang Zengping, Xu Yan, Wang Xue, et al.Study on the novel transformer protection principle based on the transformer model[J].Proceedings of the CSEE,2003, 23(12): 54-58.

[13]张保会, 尹项根.电力系统继电保护[M].北京: 中国电力出版社, 2005.

[14]冈萨雷斯, 等.数字图像处理[M].2版.阮秋琦, 等译.北京: 电子工业出版社, 2003.

[15]王雪, 王增平.基于有限元法的变压器电感参数计算方法的研究[J].电力系统保护与控制, 2009,37(24): 11-14.Wang Xue, Wang Zengping.An investigation on transformer inductance calculation based on finite element method[J].Power System Protection and Control, 2009, 37(24): 11-14.