双输入Buck变换器的单周期控制

杨东升 杨 敏 阮新波

（南京航空航天大学航空电源重点实验室 南京 210016）

1 引言

开发和利用可再生能源是缓解能源危机、解决环境污染的重要途径之一，因此受到了越来越广泛的关注。可再生能源具有廉价、可靠、清洁无污染、可永续利用等优点，但大多数可再生能源受环境和天气的限制，存在随机性和间歇性的特点，因此通常将多种具有互补特性的可再生能源发电单元结合起来，构成可再生能源联合发电系统，向用户提供稳定连续的电能[1-3]。

在可再生能源联合发电系统中，采用一个多输入直流变换器（Multiple-Input DC-DC Converter，MIC）代替传统的多个单输入直流变换器，可以简化电路结构，降低系统成本[4-6]。MIC是一种将多个输入源联合起来向单个负载供电的变换器。由于存在多个输入源，可以进行能量管理，既要保证输出电压的稳定又要实现输入功率的分配。因此MIC的控制系统将由多个闭环构成，通常包含一个电压环和多个电流环。其中电压环用来稳定输出电压，而多个电流环分别控制各个输入源的输入电流从而控制其输入功率[7-9]。由于 MIC共用输出滤波器等元件，在多个输入源同时向负载供电的工作模式下，这多个闭环之间存在相互耦合。而且根据可再生能源供电状态以及负载条件的不同，MIC通常存在多个工作模式，因此闭环系统设计比较复杂。

如果环路之间的耦合很弱，将近似认为是解耦的系统，各个环路的调节器可单独设计[10-11]。但是如果这种耦合较强，就不能忽略它们之间的相互影响。文献[12]以双输入Buck变换器为例，提出了多种模式下耦合控制系统的闭环设计方法。该变换器存在三种工作模式，其中两种模式只存在一个单电压环或者一个由电压外环和电流内环构成的双环，而另一个模式存在两个耦合的闭环。该文献首先在前两种工作模式下设计输出电压和输入电流闭环调节器，然后将调节器参数代入后一个工作模式的两路耦合的闭环中，检验其稳定性和快速性。这种方法由于存在反复校验的过程，设计过程比较复杂。

解耦法是设计耦合控制系统的一种有效方法。通过在控制回路中增加解耦矩阵，将原耦合系统的传递函数矩阵化为对角阵的形式，使每一个输出只受到一个输入的作用。解耦矩阵是该对角阵与原系统传递函数矩阵的逆的乘积，与原系统传递函数矩阵有关。由于MIC存在多个工作模式，在不同的工作模式下，系统的传递函数矩阵各不相同，因此其解耦矩阵也不相同[13]。即使在同一个工作模式下，当输入源电压和负载变化时，传递函数矩阵的系数也会发生变化，解耦矩阵的系数需要相应调整[14-15]。因此，解耦矩阵的实现是比较困难的。

上述文献均采用传统的线性反馈控制，因此需要电压调节器和电流调节器，并且任何扰动必须传递到输出后，调节器才能对误差进行校正，系统的动态响应速度受到了限制。文献[16]提出了一种非线性的单周期控制技术，其突出优点是在一个开关周期内，有效抑制输入扰动，使受控量的平均值恰好等于或正比于基准值；另一个优点是受控量为开关变量，采用单周期控制无需调节器[17]。该控制方法正适合用来控制多输入直流变换器，以解决耦合控制系统中调节器设计的难题。需要指出的是，由于单周期控制只能对开关变量或者可以转化为开关形式的变量进行控制，因此其应用受到一定的局限。

本文将单周期控制方法应用于MIC，并以双输入 Buck变换器为例，首先根据能量管理的要求定义不同的工作模式，然后给出各模式下单周期控制的具体实现方式，并提出模式之间平滑切换的方法。在此基础上，推导各工作模式下 MIC的小信号模型，并对闭环进行设计。在实验室设计了一台800W的原理样机，并进行了实验验证，实验结果表明本文所提出的单周期控制方法和闭环设计是正确的。

2 双输入Buck变换器的能量管理

图1给出了双输入 Buck变换器的电路图，其中 Vin1和 Vin2分别是1#、2#源输入电压，Q1、Q2为开关管，VD1、VD2为续流二极管，Lf是输出滤波电感，RLf是输出滤波电感的寄生电阻，Cf是输出滤波电容，RCf是输出滤波电容的等效串联电阻，RLd是负载电阻。

图1 双输入Buck变换器Fig.1 Double-input buck converter

根据图1可知，该变换器的输出电压和两个输入源的平均输入电流分别为

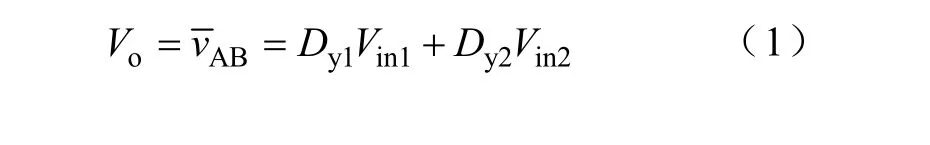
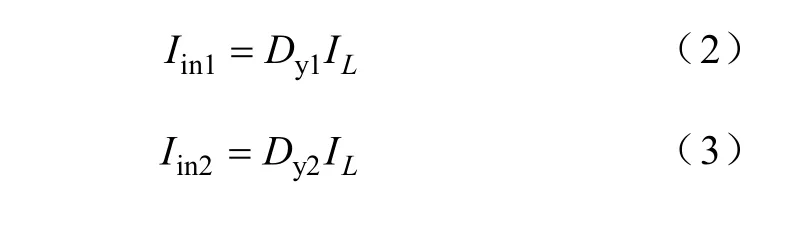
式中，Dy1和 Dy2分别为 Q1和 Q2的占空比的稳态值。

由于双输入 Buck变换器存在两个占空比，因此除了能够调节输出电压，还可以对两个输入源的输入功率进行合理分配。例如，在光伏电池/市电联合发电系统中，两个输入源分别为光伏电池和市电。由于太阳能为可再生能源，应优先利用，因此将光伏电池作为主供电电源，而市电作为备用电源。其能量管理的思路是:①光伏电池不足以提供负载所需功率时，应尽可能多地利用太阳能，让其工作在MPPT状态，以最大功率输出，市电则提供不足的负载功率；②光伏电池足够提供负载所需功率时，由光伏电池单独向负载供电，工作在稳压模式以稳定输出电压，市电退出工作。本文定义1#源为可再生能源，2#源为备用能源，设1#源所能提供的最大功率为P1max，负载所需功率为Po。根据能量管理的要求，双输入Buck变换器存在以下两种工作模式:

工作模式 I:当 P1max＜Po，两个输入源同时向负载供电，其中1#源以最大功率输出，2#源提供不足的功率。

工作模式II:当P1max＞Po时，2#源退出工作，由 1#源单独向负载供电。此时 1#源不再工作在MPPT状态，其输入功率由负载决定。

3 双输入Buck变换器的单周期控制

下面将根据上述的能量管理和工作模式，给出双输入Buck变换器单周期控制的实现方法。

3.1 工作模式I下的单周期控制

在工作模式I下，两个占空比分别用来调节1#源的输入电流iin1和输出电压vo。由式（2）可知，iin1只能由占空比dy1调节，因此占空比dy2用来调节vo。该模式下的单周期控制器电路和其工作波形分别如图2和图3所示。

3.1.1 1#源输入电流的单周期控制

1#源输入电流单周期控制器如图2a所示，它由反向器、反向积分器、比较器、RS触发器以及复位开关Sr1组成。其中iin1_f为1#源输入电流采样信号，采样系数为kif，反向器对其进行反向，以使反向积分器的输出为正向的积分电压，然后与电流基准iref比较，其主要波形如图3所示。

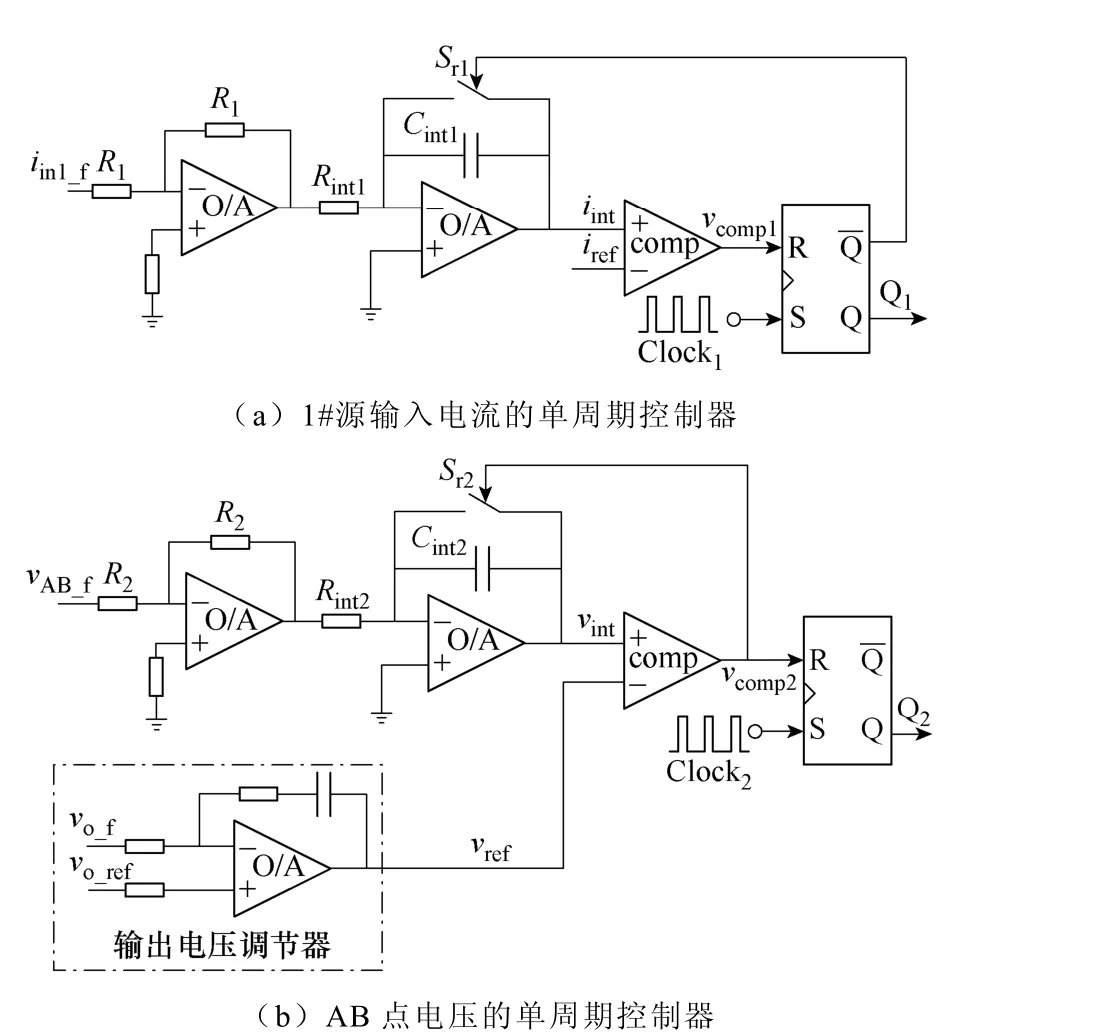
图2 工作模式I下的单周期控制电路Fig.2 Control circuit of OCC controllers in operating mode I

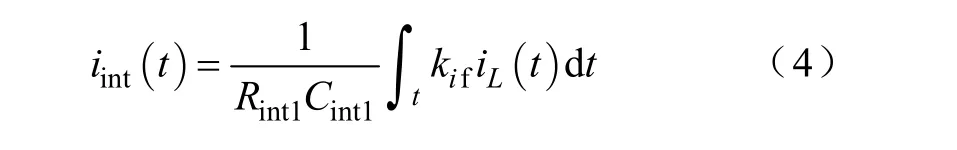
当 iint达到电流基准信号 iref时，比较器的输出信号vcomp1变成高电平，使RS触发器复位，其Q端输出低电平，关断Q1，同时端变成高电平，使 Sr1闭合，将电流积分量 iint复位为 0，直至下一个时钟脉冲的到来。故1#源输入电流的平均值为

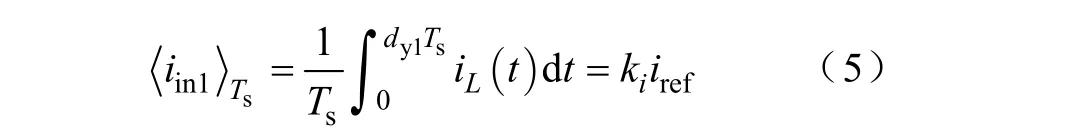
式中，Ts为时钟周期，亦即开关管的开关周期；ki=Rint1Cint1/(kifTs)。

由式（5）可以看出，采用单周期控制能够在一个开关周期内使 iin1的平均值跟踪基准值，从而消除了输入电压变化、负载突变以及另一个占空比dy2变化对iin1的扰动，且不需要电流调节器。

1#源输入电流的基准 iref可由 MPPT控制器给出，使1#源工作在最大功率输出状态，限于篇幅，本文不再对MPPT控制器作详细分析。

3.1.2 AB点平均电压的单周期控制

从图 1可以看出，A、B两点之间的电压 vAB的波形由两只开关管的开关状态确定，其平均值与Q2的开关状态没有绝对的对应关系。如图3b所示，当 Q2关断时，如果 Q1在导通，则 vAB不为零，故Q2导通的时间段对vAB进行积分不能获得一个开关周期内 vAB的平均电压的信息，因此，需要在整个开关周期内积分，复位信号在保证积分电压可靠归零的前提下，尽可能缩短复位时间。图 2b给出了vAB的单周期控制电路，其中 vAB_f为 AB点电压采样信号，采样系数为kvf。与1#源输入电流单周期控制器不同的是，其复位信号是比较器的输出，为一个窄脉冲信号，使积分器复位后能立刻重新开始积分，从而保证在整个开关周期都能对vAB进行积分，其主要波形如图3所示。

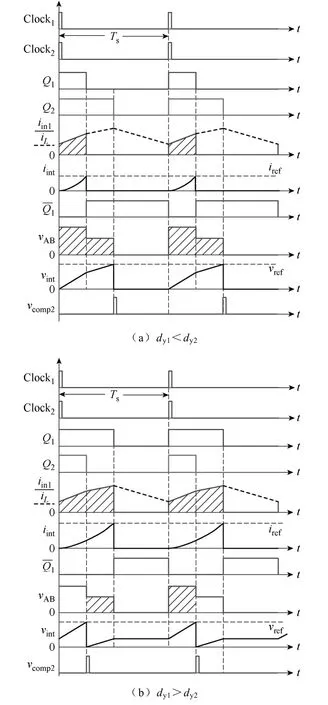
图3 工作模式I下单周期控制器的主要工作波形Fig.3 Key waveforms of OCC controllers in operating mode I

在时钟信号Clock2的上升沿开通Q2，积分器从上一个开关周期 Q2的关断时刻开始对 vAB进行积分，则其积分量vint为

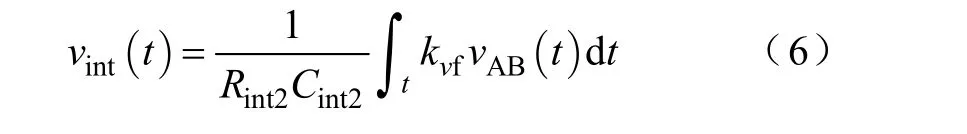
当vint达到电压基准vref时，比较器的输出信号vcomp2变为高电平，使RS触发器复位，其输出信号Q变为低电平，使Q2关断；同时vcomp2将积分电容电压复位。当积分电容电压复位时，vint低于基准vref，比较器的输出信号 vcomp2马上跳回低电平，积分器开始下一个开关周期的积分。vAB的平均值为

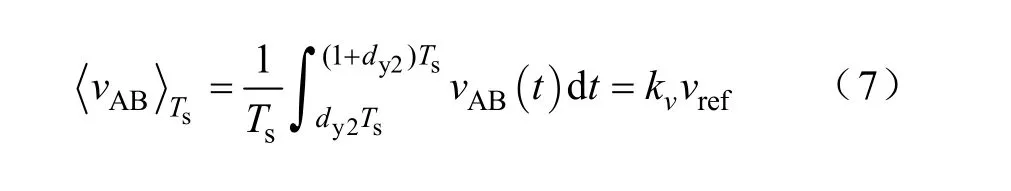
式中 kv=R2Cint2/（kvfTs）。

由式（7）可以看出，采用单周期控制能够在一个开关周期内使 AB点电压的平均值跟踪基准值，消除了输入电压和负载变化以及另一个占空比 dy1变化对vAB平均值的扰动。

由于输出滤波器存在线路阻抗，输出电压并不能精确等于 vAB的平均值，因此需加入输出电压调节器，并将其输出作为AB点电压单周期控制器的基准vref，以实现输出电压的精确调节。

3.2 工作模式II下的单周期控制

在工作模式II下，由于1#源可以单独为负载提供所需的能量，因此2#源将退出工作。也就是说，此时2#源所对应的开关管Q2将关断，即dy2=0，而1#源不再工作在MPPT模式，其占空比用来调节输出电压。其控制电路和主要波形如图4所示。其中AB点电压单周期控制器与工作模式I的基本相同，区别仅在于其输出是用来控制开关管Q1。

3.3 模式切换

由图3和图4可知，在两个工作模式下，两只开关管是由不同的单周期控制器控制，因此需要增加合适的模式切换电路。最简单的办法是增加一个模拟选通开关，如图5所示。当模拟选通开关的使能信号EN为低电平时，Ao=AX，Bo=BX，此时开关管 Q1由 1#源输入电流单周期控制器控制，开关管Q2由AB点电压单周期控制器控制。当使能信号EN为高电平时，Ao=AY，Bo=BY，此时Q1由AB点电压单周期控制器控制，而Q2的驱动信号为低电平，即Q2完全关断。

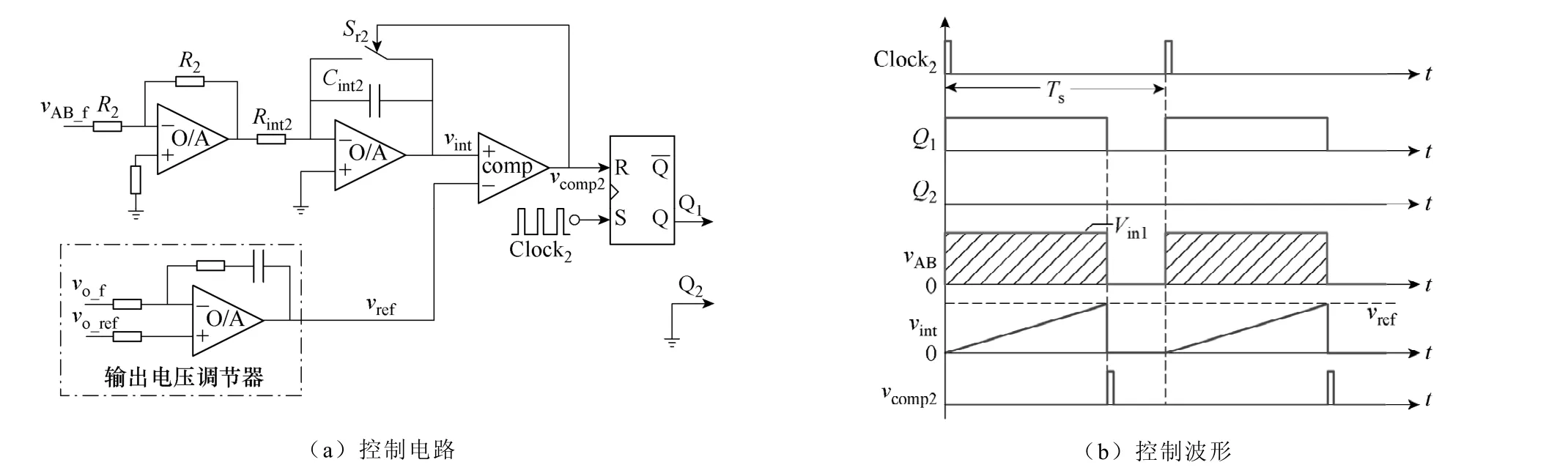
图4 工作模式II下的单周期控制Fig.4 OCC control in operating mode II

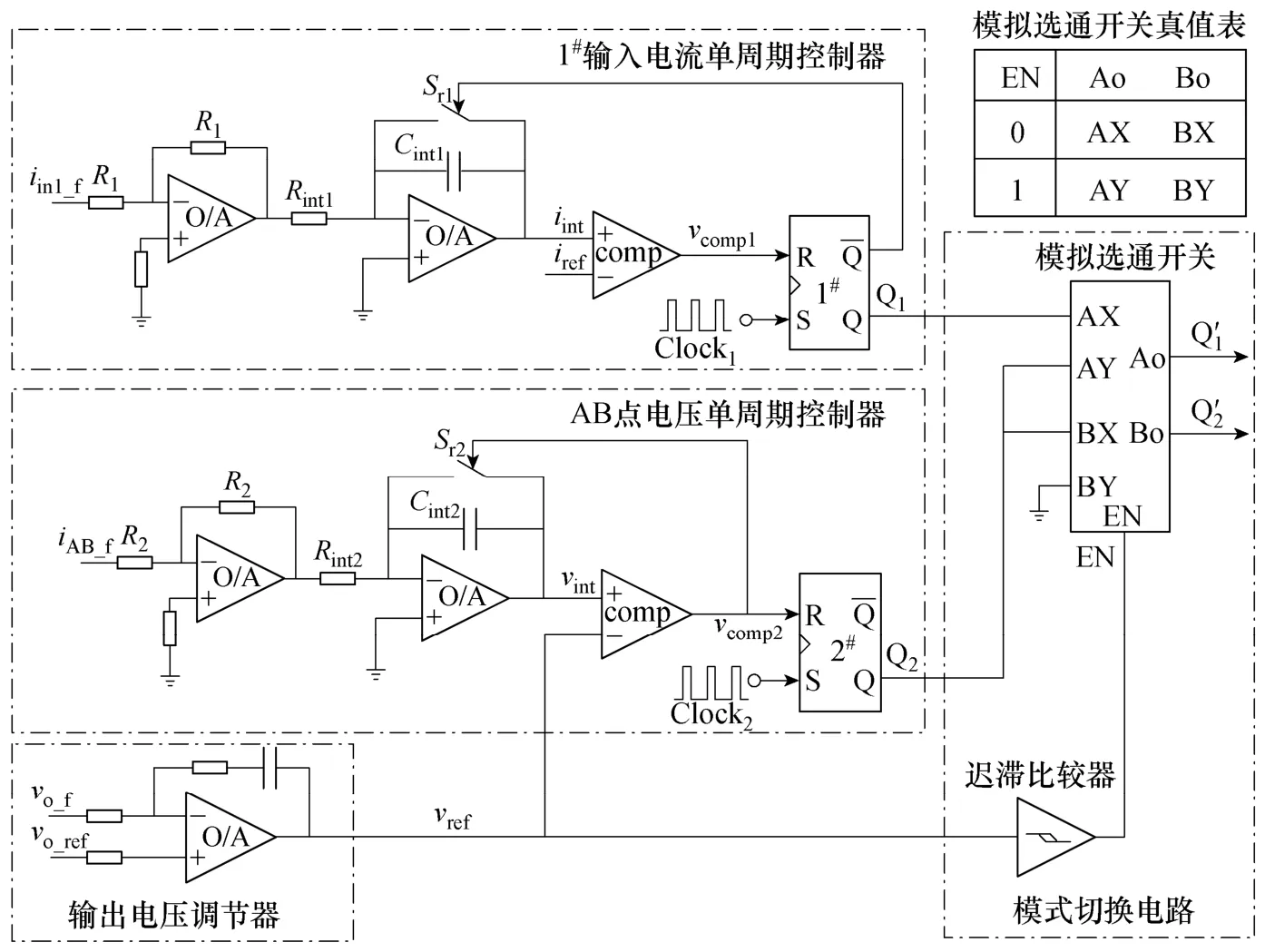
图5 多工作模式下的单周期控制电路Fig.5 OCC circuit with multiple operating modes

关键问题是如何选择合适的控制信号来控制使能信号 EN，使变换器能够在两个工作模式之间平滑切换。因为输出电压保持不变，所以无论变换器是工作在模式 I还是模式 II，在稳态时输出电压调节器的输出信号vref都相同，等于稳态值Vref，该稳态值正比于输出电压。当P1max＜Po时，变换器工作在模式I，如果1#源的最大输出功率P1max突然增加或者负载电流io突然减小，使得P1max＞Po，那么输出电压将会升高，输出电压调节器的输出 vref将会下降，直至变换器切换到模式 II。之后输出电压被调节至给定值，vref也回到稳态值 Vref。当 P1max＞Po时，变换器工作在模式II，如果1#源的最大输出功率 P1max突然减小或者负载电流 io突然增加，使P1max＜Po，那么输出电压将会降低，使输出电压调节器的输出vref上升，直至切换到模式I。之后输出电压被调节至给定值，vref也回到稳态值Vref。

从上面的分析可以看出:当变换器从模式 I切换到模式 II时，输出电压调节器的输出 vref将会有一个下降过程；反之，当变换器从模式II切换到模式I时，输出电压调节器的输出vref将会有一个上升过程。但值得注意的是，当工作模式切换以后进入稳态时，vref将会回到其稳态值Vref。根据这个特点，可以将 vref送入一个迟滞比较器，而将其输出作为使能信号 EN，如图 5所示。迟滞比较器的特性如图 6所示，其滞环中心值为 Vref，滞环宽度为ΔV。采用迟滞比较器后，稳态时，使能信号 EN由于滞环的作用保持不变，而在模式切换时，vref将不断增加或减小，直至达到滞环的门限电平，从而改变迟滞比较器输出EN的状态，如图7所示。从图中可以看到，滞环宽度ΔV的大小对于模式切换并不关键，换句话说，无论ΔV取值如何，vref总是会达到滞环的门限电平，本文实验将ΔV设置为2V。

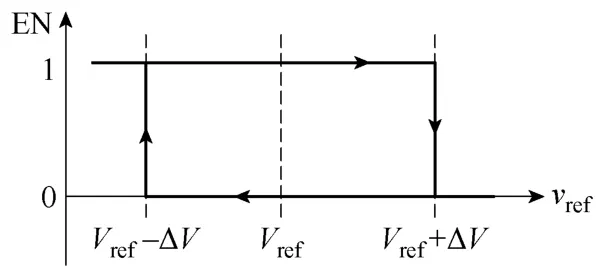
图6 迟滞比较器的特性Fig.6 The characteristic of the Schmitt trigger

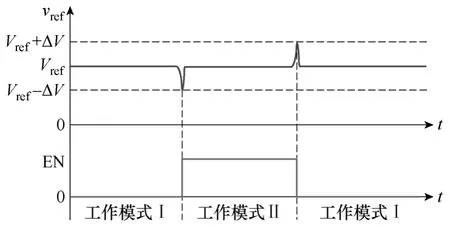
图7 模式切换的vref的动态波形Fig.7 The transient of vref during the mode transition

4 系统建模与闭环设计

在进行闭环系统设计前，首先要建立被控对象的小信号模型。下面对两种工作模式下单周期控制的双输入 Buck变换器进行小信号建模。设输出电压 vo的采样系数为 kf，电压调节器的传递函数为Gvr(s)。

在工作模式I下，两路输入源同时向负载供电，假设每个变量由稳态值和扰动量两个分量组成，即

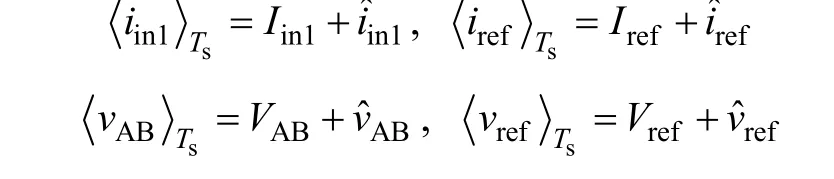
将它们分别代入式（5）和式（7），可以推出

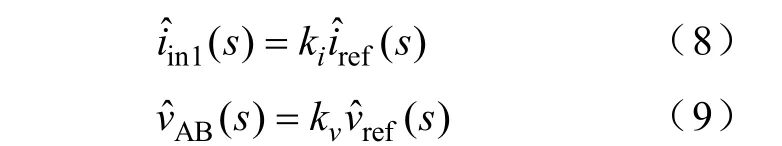
由图1可知，对于双输入Buck变换器，有

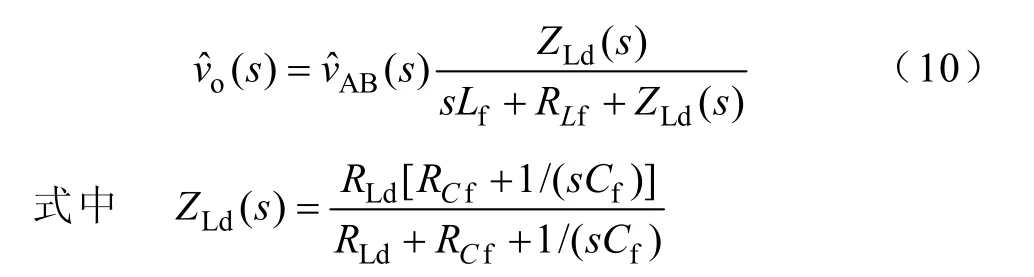
由式（8）～式（10）可得此模式变换器的小信号数学模型，如图 8a所示。从图中可以看出，1#源输入电流iin1大小与控制量vref无关，而输出电压vo与控制量iref也无关，因此两个环路互不干扰，消除了两个输入源共用输出滤波器而导致的控制环路的耦合。

在工作模式II下，1#源单独向负载供电，dy2= 0。此时双输入 Buck变换器可等效为一个单输入 Buck变换器。其控制电路只存在输出电压闭环，其中电压调节器的输出作为电压单周期控制的基准信号，以稳定输出电压。在工作模式II，式（9）和式（10）仍然成立，因此其小信号数学模型如图8b所示。

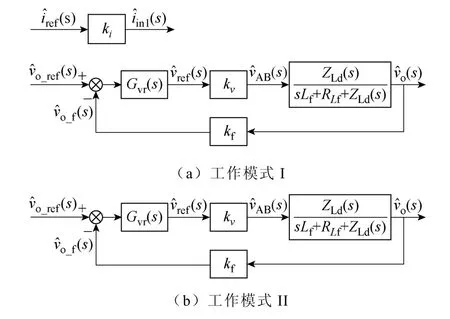
图8 小信号模型Fig.8 Small signal models

由图5可知，1#源输入电流采用单周期控制时不需要电流调节器，因此仅输出电压调节器需要设计。从图8中可以看出，输出电压环在两种工作模式下的小信号模型完全一样，其环路增益为

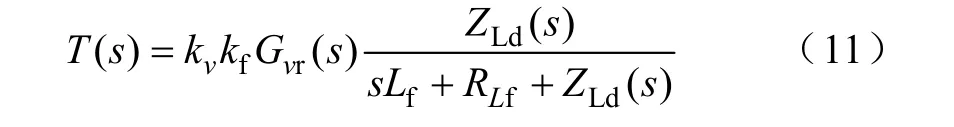
由于两种工作模式的负载条件范围一致，都要能提供额定功率，故均按照满载情况设计，两种工作模式下电压环的设计条件相同。变换器主电路和单周期控制器采用的电路参数见第5节。

令 Gvr(s)=1，根据式（11）可以得到补偿前电压闭环的环路增益的Bode图，如图9中虚线所示。从中可以看出，补偿前的低频增益曲线平坦，幅值较低，仅为6dB左右，而且截止频率仅为560Hz，相位裕度为 20º。为提高低频环路增益以减小稳态误差，并且提高截止频率以提高系统的动态性能，本文选择PI调节器进行补偿，其传递函数为

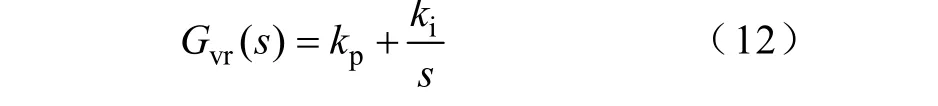
本文选取截止频率 fc为 1/10的开关频率，即10kHz。同时由于输出滤波器的电感和电容存在谐振频率点，造成180º的相位滞后，因此为避免调节器在该谐振频率点处引起更多的相位滞后而导致相角穿越-180º，将PI调节器的零点所对应的频率设定在的1/10的谐振频率处。因此电压调节器相应参数为:kp= 135，ki= 2.5×104。补偿后电压环环路增益函数的频率特性如图9中的实线所示，从中可以看出，补偿后的截止频率为10kHz，相位裕度为76º，满足稳定性和快速性要求。

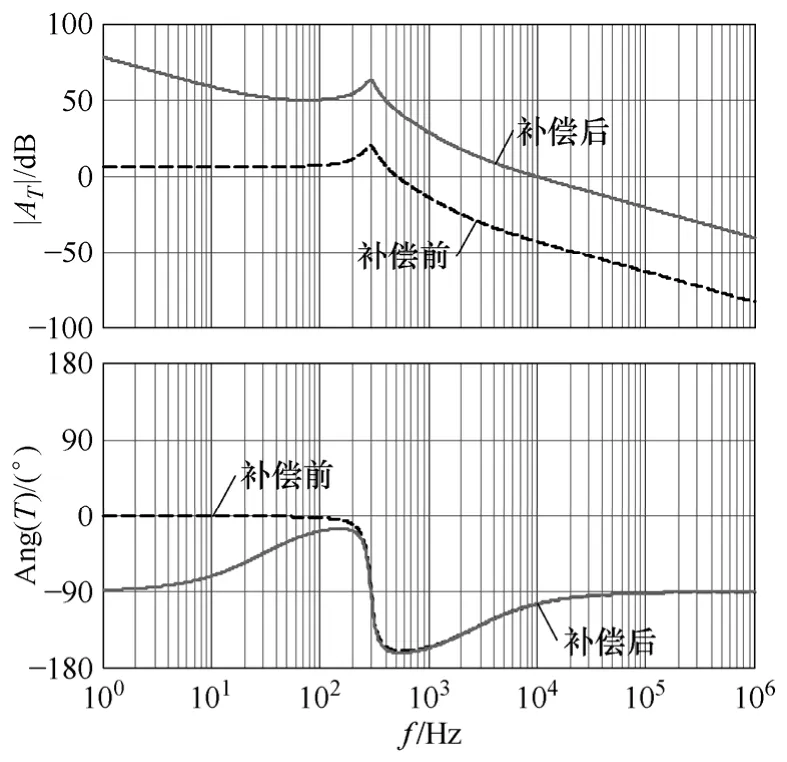
图9 工作模式I、II下电压环开环环路增益的频率特性Fig.9 Output voltage loop gain in operating modes I and II

5 实验结果

为了验证所提出的控制方法的正确性和闭环设计的有效性，在实验室完成了一台800W的双输入Buck变换器的原理样机。其中主电源和备用电源分别为光伏电池和整流后的AC220V单相市电，整个实验的系统框图如图10所示。本文样机的主要技术指标如下:

所采用的主要电路参数如下:

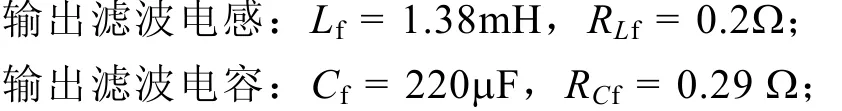
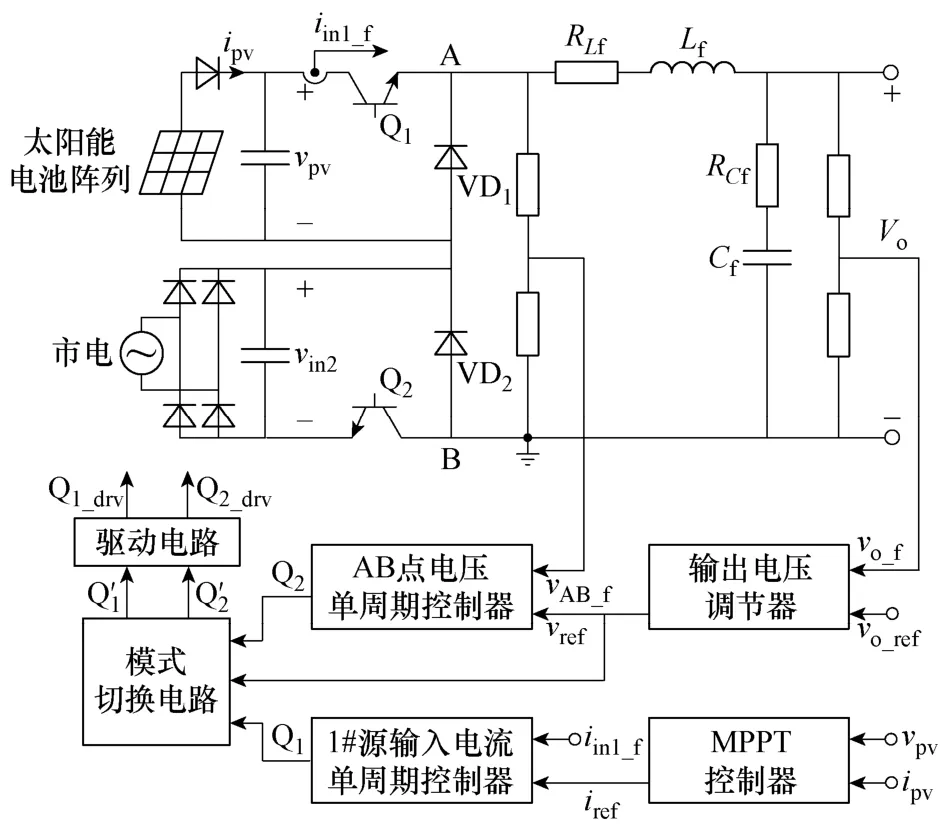
图10 实验系统框图Fig.10 The block diagram of the whole experimental system

5.1 单周期控制的稳态实验验证

图11给出了两种工作模式下，开关管驱动信号vGS1和vGS2、1#源的输入电流iin1以及它的积分值iint和积分基准 iref、AB点电压 vAB和它的积分值 vint和积分基准vref的稳态实验波形。

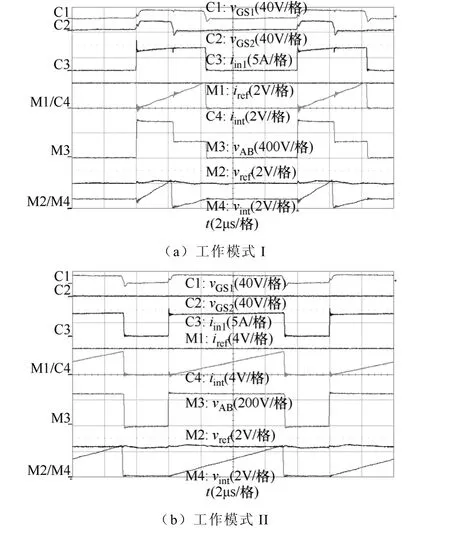
图11 稳态实验波形Fig.11 Experimental waveforms at steady-state

图11a为由两个源同时向负载供电的情况，其中1#源输入电流单周期在Q1开通时对1#源的输入电流进行积分，当积分值iint到达电流基准时立即进行复位，关断 Q1，从而保证 1#输入电流的平均值精确地等于电流基准。类似地，AB点电压单周期是在Q2关断时开始对AB点电压进行积分，当积分值 vint到达电压基准立即复位，关断 Q2，同时开始下一个周期的积分，从而保证AB点电压精确地等于电压基准。由于电压基准是由输出电压调节器给出，因此它会根据输出电压的变化进行一定的调节。

图11b为光伏电池单独向负载供电的情况，此时 2#源退出工作，Q2占空比为 0，由 AB点电压单周期控制器代替 1#源输入电流单周期控制器来调节Q1的占空比从而稳定输出电压。同样地，AB点电压单周期控制器在 Q1关断时立刻对 AB点电压进行积分，从而控制AB点电压精确地等于电压基准。而此时电流单周期控制器不控制任何变量。

由此可验证单周期控制器工作原理的正确性。

5.2 单周期控制的动态实验验证

为验证采用单周期控制方法能够消除多个环路之间的相互耦合干扰，本文分别给出了负载突变和P1max突变时的实验波形，如图12和图13所示。为了进行对比，本文还给出了在相同测试条件下，采用传统的线性反馈控制[11]时的实验波形。

图12 负载跳变实验波形Fig.12 Experimental waveforms corresponding to a step change of load current

图12给出了 P1max为 500W 时，负载功率在700W 和 800W 之间跳变的实验波形。采用传统的线性反馈控制时，如图12a所示，在负载跳变的时刻，输出电压环对输出电压进行调节，但该过程会同时影响1#源输入电流电流环，使其平均值存在扰动。但是采用单周期控制时，如图12b所示，1#源输入电流的平均值总是等于基准值，不受输出电压环的影响。

图13给出了负载功率为满载 800W 时，P1max在400W（Iin1= 1.6A）和500W（Iin1= 2A）之间跳变的实验波形。此时，1#源输入电流的基准 iref由MPPT控制器调节，使1#源以最大功率输出。为清楚地观察动态情况，输出电压采用交流档测量。采用传统的线性反馈控制时，如图 13a所示，在 1#源输入电流环调节时，输出电压环会受影响，故输出电压存在扰动。而采用单周期控制时，由于AB点电压的平均值在单个开关周期就能调节至基准值，故输出电压不受 1#源输入电流变化的影响，如图 13b所示。因此由图 12和 13可知，采用单周期控制可以消除电压环和电流环之间的相互干扰。

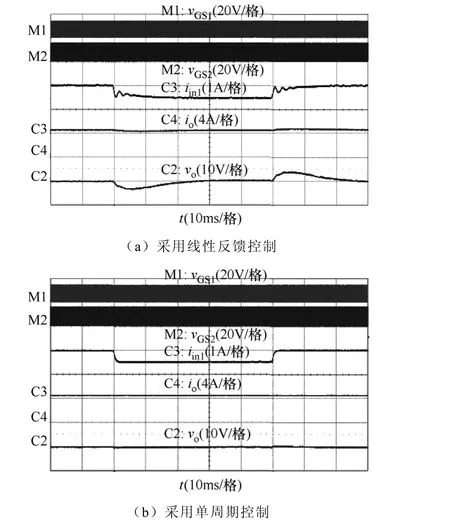
图13 P1max跳变实验波形Fig.13 Experimental waveforms corresponding to a step change of P1max

5.3 模式切换的验证

为验证采用模式切换电路后，双输入 Buck变换器能够在工作模式之间平滑切换，以实现可再生能源优先利用，本文分别给出了负载功率Po突变和光伏电池最大输出功率 P1max突变时的动态实验波形。

图14a给出了 P1max为 500W 时，负载在满载（Io= 4.44A）和半载（Io=2.22A）之间跳变时的动态实验波形。满载时，P1max＜Po，故光伏电池和市电同时向负载供电:光伏电池以最大功率输出，对应输出电流iin1的平均值为2A，市电提供剩余功率。当负载跳为半载时，P1max＞Po，输出电压升高，输出电压调节器的输出 vref下降，使迟滞比较器的输出 EN从低电平变为高电平，变换器由工作模式 I切换至工作模式II，之后vref又回到稳态值Vref，如图中虚线圈所示。此时开关管Q2完全关断，由光伏电池单独向负载供电，其实际输出功率由负载决定，对应的输出电流iin1的平均值为1A。当负载恢复到满载时，P1max＜Po，输出电压下降，输出电压调节器的输出vref上升，使迟滞比较器的输出EN从高电平变为低电平，切换至工作模式I，之后vref又回到稳态值。光伏电池恢复到最大功率输出，开关管Q2开通，市电提供剩余功率。在负载跳变前后，输出电压均能稳定在180V。

图14b给出了负载功率为满载 800W时 P1max在500W和900W之间跳变时的动态实验波形。当P1max为 500W 时，P1max小于 Po，故光伏电池和市电同时向负载供电:光伏电池以最大功率输出，对应输出电流iin1的平均值为2A，市电提供剩余功率。当P1max突变为900W时，P1max＞Po，输出电压升高，输出电压调节器的输出 vref下降，使迟滞比较器的输出 EN从低电平变为高电平，变换器由模式 I切换至模式 II，之后 vref又回到稳态值，如图中虚线圈所示。此时开关管Q2完全关断，由光伏电池单独向负载供电，其实际输出功率由负载决定，对应输出电流 iin1的平均值为3.6A。当P1max恢复到500W时，P1max＜Po，输出电压下降，输出电压调节器的输出vref上升，使迟滞比较器的输出EN从高电平变为低电平，切换至工作模式I，之后vref又回到稳态值。光伏电池恢复到最大功率输出，开关管Q2开通，市电提供剩余功率。在P1max跳变前后，输出电压均能稳定在180V。

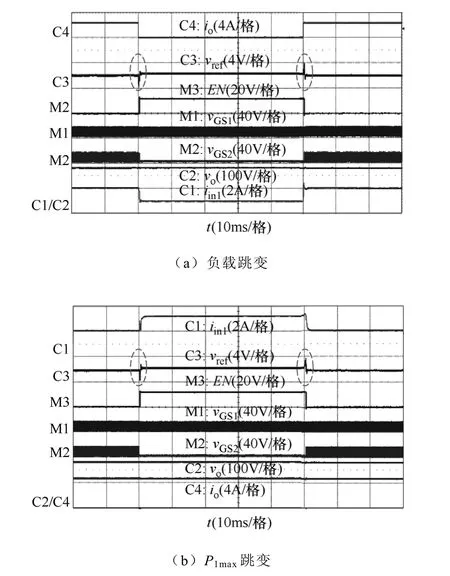
图14 模式切换实验波形Fig.14 Experimental waveforms of mode transition

需要指出的是，由于单周期控制器中积分器的复位总是需要一定的时间。因此在工作模式 I下，积分器在这段复位时间段内无法对AB点电压进行积分，如图11a所示。但是输出电压调节器对这个积分误差进行了校正，因此 vref的稳态值在两个工作模式下会有较小的调整。

由此可见，模式切换电路能够根据光伏电池最大输出功率 P1max和负载所需功率 Po的关系在两个模式之间平滑切换。

6 结论

采用多输入直流变换器构成可再生能源联合发电系统，可简化电路结构，降低系统成本。由于能量管理的要求，该系统通常存在多个工作模式，并且在多个输入源同时向负载供电时，它是一个典型的多输入-多输出的耦合系统，因此闭环设计复杂。

以双输入 Buck变换器为例，本文采用单周期控制方法消除了闭环之间的相互干扰，从而简化了闭环设计。本文给出了各个工作模式下单周期控制电路和模式切换电路的实现方法。通过对该变换器建模分析可知，采样单周期控制和所提出的模式切换方式无需电流调节器，并且输出电压调节器在不同工作模式下的设计条件相同，因此闭环设计过程大大简化。最后通过一台800W原理样机验证了所提出的单周期控制方法的稳态和动态性能。

[1]Kim S K, Jeon J H, Cho C H, et al.Dynamic modeling and control of a grid-connected hybrid generation system with versatile power transfer[J].IEEE Transactions on Industry Electronics, 2008, 55(4):1677-1688.

[2]Wang C S, Nehrir M H.Power management of a stand-alone wind/photovoltaic/fuel cell energy system[J].IEEE Transactions on Energy Conversion,2008, 23(3): 957-967.

[3]Valenciaga F, Puleston P F.Supervisor control for a stand alone hybrid generation system using wind and photovoltaic energy[J].IEEE Transactions on Energy Conversion, 2005, 20(2): 398-405.

[4]Chen Y M, Liu Y C, Lin S H.Double-input PWM dc-dc converter for high/low voltage sources[J].IEEE Transactions on Industry Electronics, 2006, 53(5):1538-1544.

[5]Qian Z J, Abdel-Rahman O, Batarseh I.An integrated four-port dc-dc converter for renewable energy applications[J]. IEEE Transactions on Power Electronics, 2010, 25(7): 1877-1887.

[6]Li Y, Ruan X B, Yang D S, et al.Synthesis of multiple-input dc/dc converters[J].IEEE Transactions on Power Electronics, 2010, 25(9): 2372-2385.

[7]Chen Y M, Liu Y C, Wu F Y, et al.Multi-input converter with power factor correction and maximum power point tracking features[C].Proceedings of IEEE Applied Power Electronics Conference, 2002:490-496.

[8]Solero L, Lidozzi A, Pomilio J A.Design of multiple-input power converter for hybrid vehicles[J].IEEE Transactions on Power Electronics, 2005,20(5):1007-1016.

[9]Benavides N D, Chapman P L.Power budgeting of a multiple-input buck-boost converter[J]. IEEE Transactions on Power Electronics, 2005, 20(6):1303-1309.

[10]Somayajula D, Ferdowsi M.Small-signal modeling and analysis of the double-input buck-boost converter[C].Proceedings of IEEE Applied Power Electronics Conference, 2010: 2111-2115.

[11]Mummadi V, Sawant K K.Control of multi-input integrated buck-boost converter[C].Proceedings of International Conference on Industrial and Information Systems, 2008: 1-6.

[12]Li Y, Ruan X B, Yang D S, et al.Modeling, analysis and design for hybrid power systems with dual-input DC-DC converter[C].Proceedings of IEEE Energy Conversion Congress and Exposition, 2009: 3203-3210.

[13]Qian Z J, Abdel-Rahman O, Al-Atrash H, et al.Modeling and control of three-port dc-dc converter interface for satellite applications[J]. IEEE Transactions on Power Electronics, 2010, 25(3):637-649.

[14]Liu D W, Li H, Marlino L D.Design of a 6 kW multiple-input bi-directional dc-dc converter with decoupled current sharing control for hybrid energy storage elements[C].Proceedings of IEEE Applied Power Electronics Conference, 2007: 509-513.

[15]Zhao C H, Round S D, Kolar J W.An isolated three-port bidirectional DC-DC converter with decoupled power flow management[J]. IEEE Transactions on Power Electronics, 2008, 23(5):2443-2453.

[16]Smedley K M, Slobodan C.One-cycle control of switching converters[J]IEEE Transactions on Power Electronics, 1995: 10(6): 625-633.

[17]Chen G Z, Smedley K M.A current source with one-cycle control and its application in serial hybrid active power filter[C].Proceedings of IEEE Power Electronics Specialists Conference, 2003: 797-802.