高精度A稳定隐式调谐Taylor级数法在电力系统中的应用

郑焕坤 常鲜戎 王正辉

（1.华北电力大学电气与电子工程学院 保定 071003 2.青海省电力设计院 西宁 810008）

1 引言

暂态稳定计算是电力系统基本计算之一。暂态稳定计算方法主要有时域仿真法、直接法和人工智能等方法[1]。时域仿真法作为研究电力系统暂态稳定计算的重要手段，具有直观、信息量丰富、物理概念清晰等优点，其难点是既要保证算法具有良好的稳定性同时又要具有足够高精度。1963年Dahlquis引入A稳定性概念的同时也提出了限制性的结果：显式的线性多步法（包括显式 Runge-Kutta方法）不可能是A稳定的；A稳定的隐式线性多步法的阶数不能超过2，而所有A稳定的2阶方法中，梯形公式具有最小的局部截断误差常数[2]。自夏道止教授 1983年将高阶 Taylor级数法引入暂态稳定计算后[9]，基于Taylor级数的暂态稳定仿真的研究一直没有中断。快速高阶Taylor级数法是一种较优秀的暂态稳定计算方法，但其数值稳定性较弱[4]。很多学者为了提高其数值稳定性和计算精度做了大量工作，例如引入多步法、隐式方法等。

隐式Taylor级数法较显式Taylor级数法稳定域明显扩大[5]。文献[6]提出了隐式调谐Taylor级数法，并根据经验试探性地引入调谐参数以改善其稳定。本文在其基础上通过数学推导，得到具有A稳定性的高精度隐式Taylor级数算法的计算格式。证明了按照本文提出的计算格式设计的隐式高阶Taylor级数在具有高计算精度的同时还可以保持良好的稳定性。通过理论推导，证明了该隐式高阶Taylor级数法在达到2N阶精度时仍然是A稳定的。该方法突破了Dahlquist提出的限制性结果。另外该方法除了适用于电力系统暂态稳定计算也适用于电力系统的中长期仿真计算。

2 隐式Taylor级数法数值计算精度分析

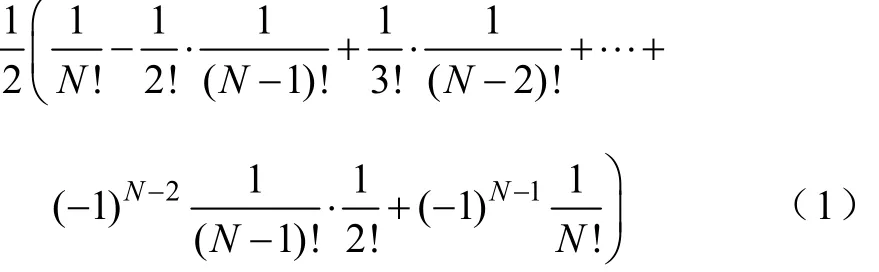
设式（1）=S，当N为偶数时易知S为零。当N为奇数时，有

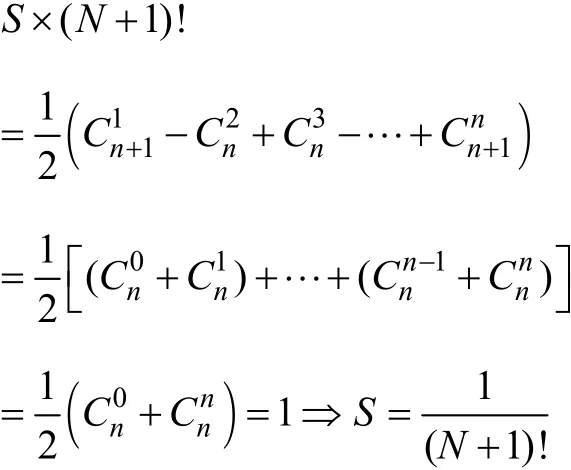
所以当N为奇数时，S=1/(N+1)！

与N+1阶奇数情形类似，可证S′=1/K！。

当N为奇数时

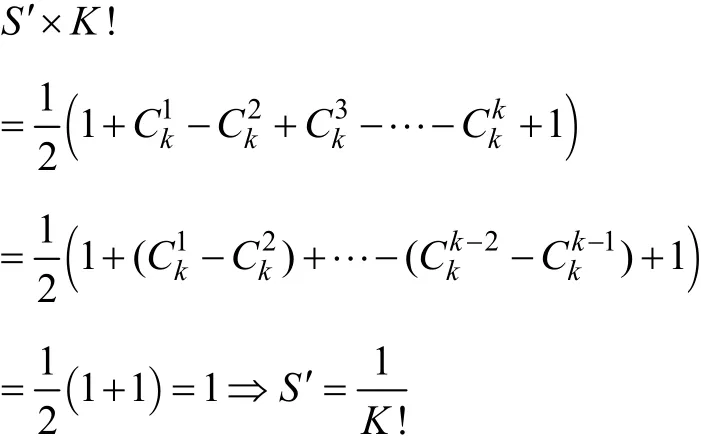
综上所述，y(1)(x+Δx )的 K阶导数的系数为1/K！ (K=1,2,⋅⋅, N)。经过以上分析后发现，展开阶数N与数值精度之间呈如下关系：当N为偶数时精度为N阶，而N为奇数时精度为N+1阶。

3 隐式Taylor级数法数值稳定性分析

P阶展开时改进隐式Taylor级数法绝对稳定域为

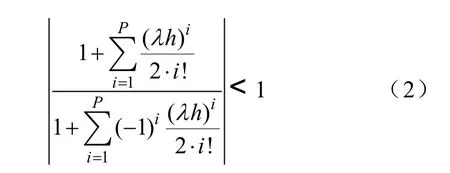
这里λ 为复数。P＝1时，隐式Taylor级数法即等价为A稳定的隐式梯形法。梯形法是二阶的方法，也是A稳定的方法中截断误差比较小的方法。当P＝1,2,3时，隐式Taylor级数法在hλ 复平面的左半平面。而当P=4时稳定域如图1中阴影所示。

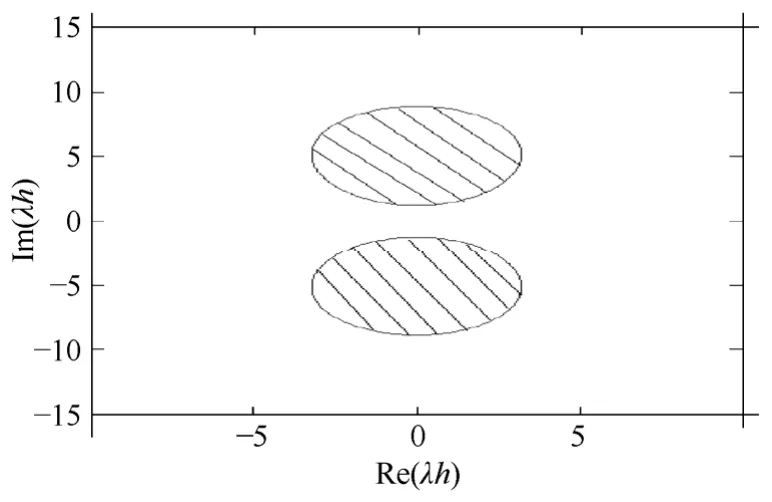
图1 P=4时隐式Taylor级数法稳定域Fig.1 Stability domain of implicit Taylor series method

隐式Taylor级数法较显式Taylor级数法稳定域明显扩大，在相同精度下，绝对稳定域也要比Runge-Kutta法大[5]。由式（2）可知在P＜4时将稳定域的范围控制在复平面的左半平面即 A稳定区域，当阶数升高（P≥4）时，隐式Taylor级数法不再具有如此良好的数值稳定性。

4 隐式调谐Taylor级数法迭代格式

为了使高精度的隐式Taylor级数法具有更强的数值稳定性，引入如下参数调节格式：

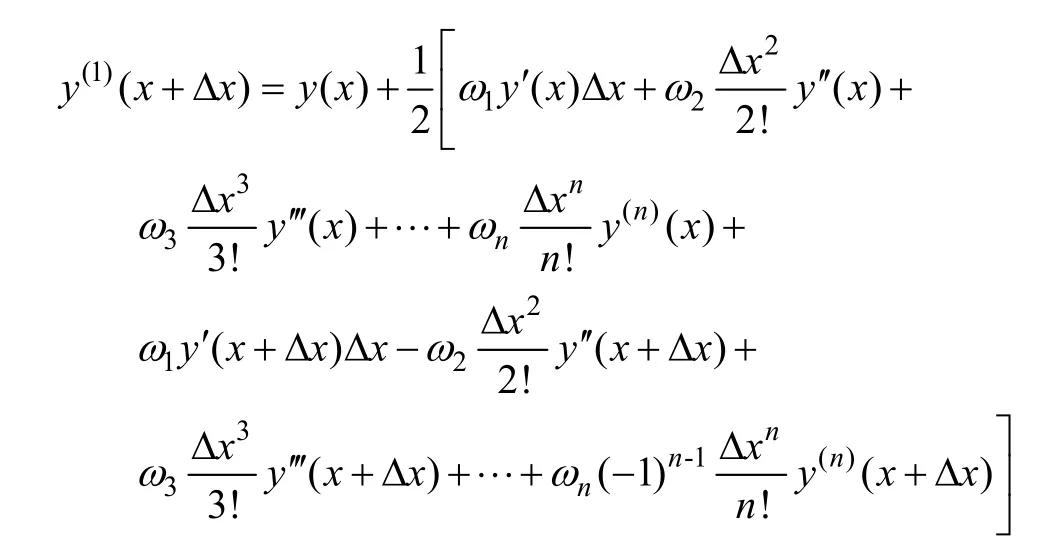
式中，ω1, ω2,…,ωn为隐式调谐Taylor级数法调节格式中待定系数。由隐式Taylor级数法迭代格式可知当展开阶数为N时，其中各调谐参数需满足条件：

以上两式中 ωi(i=1,2 … N)为N阶展开时对应于方程组（3）的解。

对应的隐式Taylor级数法绝对稳定域为

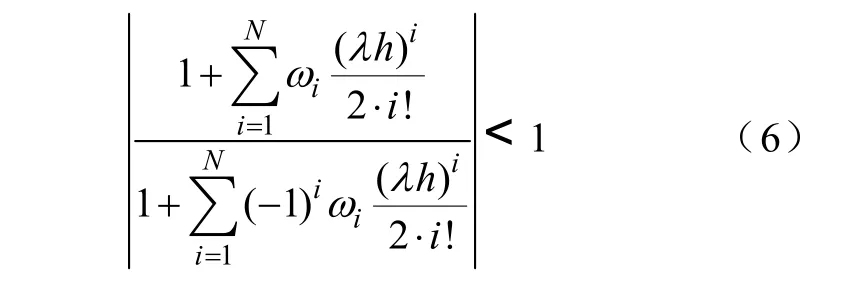
5 隐式调谐Taylor级数法算法稳定性分析

经过参数调节后所得到的上述迭代算法为A稳定的，下面给出证明。以N=4为例，由方程组（3）可知四阶展开时隐式 Taylor级数法可达 8阶精度（具体证明见调谐隐式 Taylor级数法计算精度分析）。它的稳定域为

式（8）只有当x＜0时才成立，故式（5）的解均在复平面的左边平面。因此，采用这种调谐方法的隐式Taylor级数法是A稳定的。类似可证N=5,6,⋅⋅的情形，这里不再赘述。N=5,6阶时具体稳定域分别在复平面的左半平面。

6 隐式调谐Taylor级数法计算精度分析

由隐式Taylor级数法数值计算精度分析可知：对于y=f(x)，当N为偶数时精度为N阶，而N为奇数时精度为N+1阶。对于隐式调谐Taylor级数法，以 N=4为例，由式（3）得到对应参数并与 y=f(x)隐式泰勒级数8阶展开式相减，可得（具体化简过程 从略）： y(1)(x +Δ x)-y(0)(x +Δ x)=O(Δ x9)

可见：隐式调谐Taylor级数法与y=f(x)的8阶Taylor展开式相减得到的局部截断误差为9O(Δx)。因此当隐式调谐Taylor级数法阶数为4时算法精度可达8阶。类似可分析其他展开阶数的情形。

7 隐式调谐Taylor级数法计算速度分析

在满足相同计算精度前提下，显式Taylor级数法的计算速度较常规四阶Runge-Kutta法快6倍左右[6]。由隐式调谐Taylor级数法迭代格式，可知若式（4）去掉调谐因子即为显式高阶 Taylor级数法的迭代格式。由式（4）和式（5）可知，对于隐式调谐Taylor级数法每步计算约为显式Taylor级数法的2倍。由隐式调谐Taylor级数法精度分析可知，当Taylor级数展开N阶时其计算精度为2N阶。因此，若保持隐式Taylor级数法和显式Taylor级数法计算精度相同，则相应显式Taylor级数法必须展开2N阶。而显式Taylor级数法，每一步计算量约为[10]

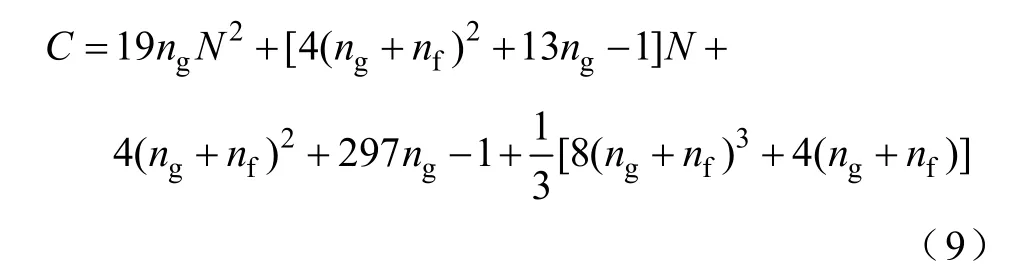
式中，ng为系统发电机个数，nf为故障点个数，N为 Taylor级数展开的阶数。由式（9）可知，当显式Taylor级数法展开阶数由N变为2N时增加的计算量还与具体系统规模有关。从本文采用的72机等效系统仿真结果可以看出，隐式调谐Taylor级数至少可以采用2倍于显式Taylor级数法的步长进行仿真，即进行相同的暂态稳定计算，隐式调谐 Taylor级数法计算步数仅为显示Taylor级数法的一半。由上述分析可知，隐式调谐Taylor级数仿真速度应略快于显式Taylor级数法。

仿真时设系统中66号发电机出口母线0s发生三相短路故障，隐式调谐Taylor级数法展开5阶，仿真步长0.06s，显式Taylor级数法展开10阶，仿真步长0.03s，进行20s仿真，隐式调谐Taylor级数法实际用时 25.6s，而显式 Taylor级数法实际用时27.1s。仿真结果验证了分析的正确性。

8 仿真计算

本文选用我国某省电力系统的等效 72机系统为实验系统。分别对显式Taylor级数法、隐式Taylor级数法和隐式调谐Taylor级数法在不同仿真步长下进行计算，并对计算结果进行分析。

8.1 小干扰仿真计算

设系统中14号发电机母线0.5s投入负荷，负荷等值阻抗Z=10+j10，并在6.2s切除该负荷，所有保护均不动作，仿真步长为0.01s，仿真结果如图2所示。

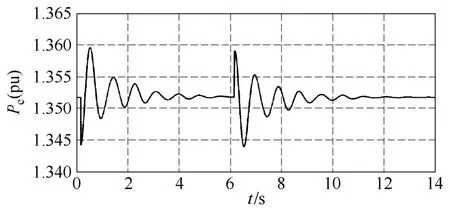
图2 隐式调谐Taylor级数法小干扰14机Pe曲线Fig.2 The Pe curve of No.14 generator with implicit tuned Taylor method when small disturbance

针对时域数值积分方法对扰动比较敏感的问题，对隐式调谐Taylor级数法进行小干扰仿真。从图2可以看出，在系统投入小负荷时发生功率振荡，并在5s时达到新稳定值1.353，切除负荷后最后稳定在未投切负荷时的1.351，未发生局部窗口失真或数值稳定性问题。利用该方法进行了大量小干扰仿真均未发现局部窗口失真或数值稳定性问题。

8.2 系统三相接地故障暂态仿真计算

设系统中66号发电机出口母线0s发生三相短路故障，0.1s故障清除，所有保护均不动作。图 3为仿真步长为 0.01s时显式 Taylor级数法、隐式Taylor级数法以及隐式调谐Taylor级数法的仿真曲线。图4、图5中仿真步长均为0.03s。图6和图7中仿真步长为0.06s。

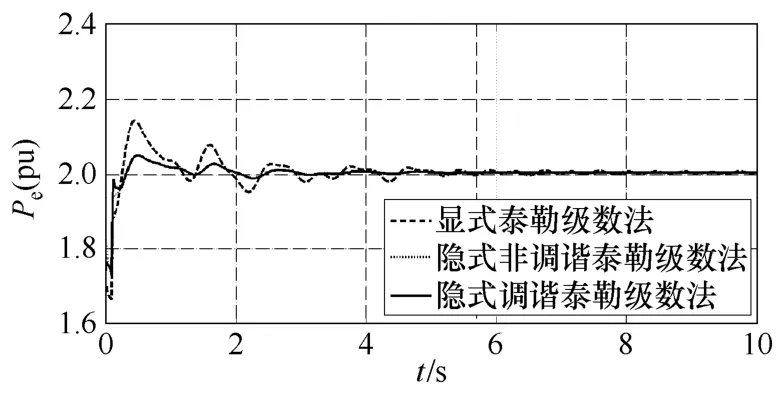
图3 显式、隐式和隐式调谐法66号机Pe曲线Fig.3 The Pe curve of No.66 generator with explicit,implicit and implicit tuned method

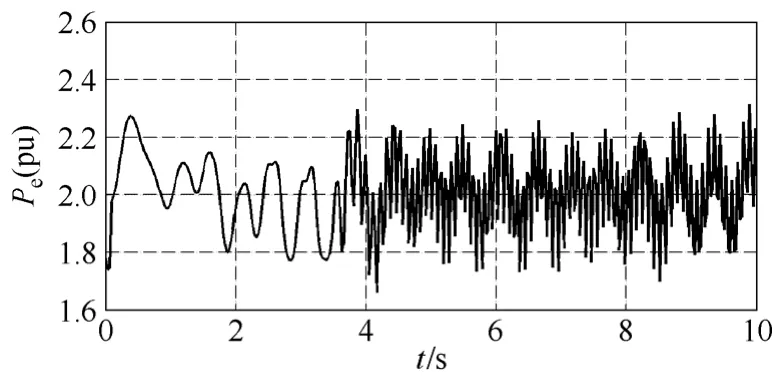
图4 显式Taylor级数法66号机Pe曲线Fig.4 The Pe curve of No.66 generator with explicit method

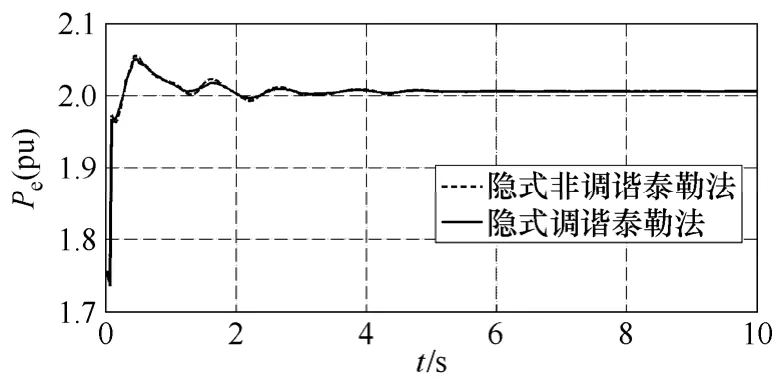
图5 调谐与非调谐Taylor级数法66号机Pe曲线Fig.5 The Pe curve of No.66 generator with implicit and implicit tuned method

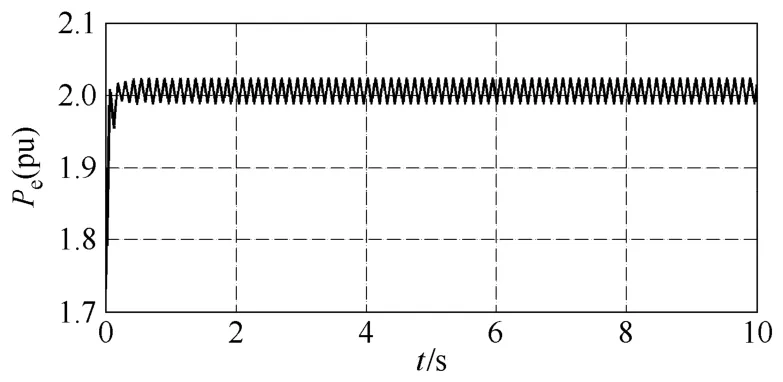
图6 隐式非调谐Taylor级数法66号机Pe曲线Fig.6 The Pe curve of No.66 generator with implicit method

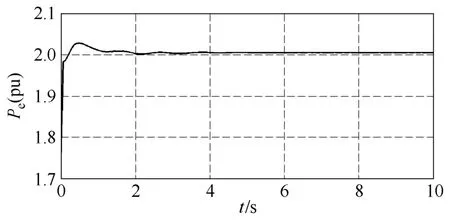
图7 隐式调谐Taylor级数法66号机Pe曲线Fig.7 The Pe curve of No.66 generator with implicit tuned method

由算例结果可以看出，显式Taylor级数法的数值稳定性较差，在取小步长时算法是稳定的，而当取较大步长时会出现“误差淹没真值”的现象，使计算无法继续。从图 3中可以看出，当步长均为0.01s时显式 Taylor级数法比隐式 Taylor级数法和隐式调谐Taylor级数法振荡的幅值大，振荡时间长。当积分步长增长到0.03s时显式Taylor级数法失去稳定，隐式Taylor级数法和隐式调谐Taylor级数法均能保持稳定；继续增加步长，当步长为 0.06s时隐式Taylor级数法也失去稳定，而隐式调谐Taylor级数法仍可以维持稳定。从图5中可以看出在相同步长情况下，隐式调谐Taylor级数法振荡幅值要小于隐式非调谐Taylor级数法。可见调谐Taylor级数法在保证较高计算精度情况下还具有很大的稳定域。

8.3 系统中长期动态仿真

对系统进行中长期仿真，设系统中243号母线0s投入负荷，负荷等值阻抗为Z=0.3+j0.8，并在30s切除该负荷，所有保护均不动作，仿真步长为0.06s，仿真结果如图8所示。

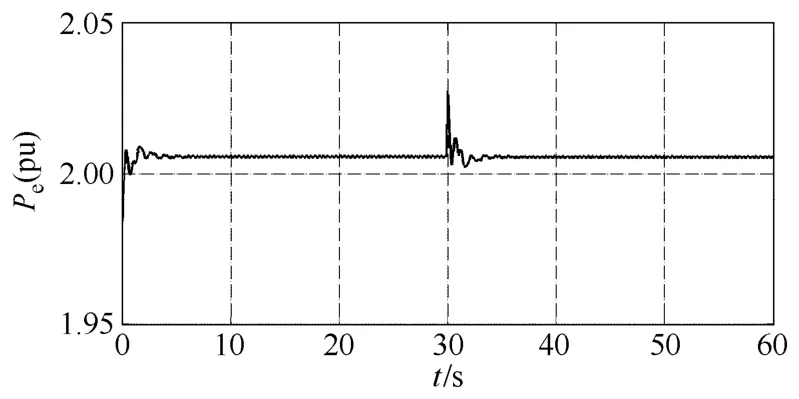
图8 隐式调谐Taylor级数法66号机Pe曲线Fig.8 The Pe curve of No.66 generator with implicit tuned method

从图8中可以看出隐式调谐Taylor级数法可以进行大步长、长时间动态仿真，因而可用于中长期的仿真。

9 结论

在隐式Taylor级数法[5]基础上，引入了隐式调谐 Taylor级数法迭代格式，通过数学推导得出了具有A稳定性的高精度隐式调谐Taylor级数法的计算格式。解决了原隐式算法高精度时数值稳定性较差的问题。当 N=2,3时调谐后即保持了原有的 A稳定性，同时又将稳定精度扩大为 2N阶。N≥4时既把稳定域扩大为A稳定同时又将计算精度提高为 2N阶。该方法突破了 Dahlquist提出的限制性结果，即隐式高阶Taylor级数算法通过调谐以后也可以在高阶保持A稳定。另外在仿真中可以使用较大的积分步长，能够适应较长动态过程仿真计算。

[1]李亦宁.电力系统暂态稳定性评估结果的稳定性研究[D].西安: 西安大学, 2008.

[2]Dahlquist G.A special stability problem for linear multistep method[J].BIT, 1963, 3(1): 27-43.

[3]王守相, 郑志杰, 王成山.计及不确定性的电力系统时域仿真的区间算法[J].中国电机工程学报,2007, 27(7): 40-44.Wang Shouxiang, Zheng Zhijie, Wang Chengshan.Power system time domain simulation under uncertainty based on interval method[J].Proceedings of the CSEE, 2007, 27(7): 40-44.

[4]郭志忠, 柳焯.快速高阶 Taylor级数法暂态稳定计算[J].中国电机工程学报, 1991, 11(3): 7-15.Guo Zhizhong, Liu Zhuo.Fast transient stability simulation by higher order Taylor series expansions[J].Proceedings of the CSEE, 1991, 11(3): 7-15.

[5]袁兆鼎, 费景高, 刘德贵.刚性常微分方程初值问题的数值解法[M].北京: 科学出版社, 1987.

[6]王宇兵, 常鲜戎, 罗艳, 等.基于隐式 Taylor级数法的电力系统暂态计算[J].华北电力大学学报,2005, 32(2): 1-6.Wang Yubin, Chang Xianrong, Luo Yan, et al.An implicit Taylor series method for simulation of power system transient[J].Journal of North China Electric Power University, 2005, 32(2): 1-6.

[7]Furuya S, Iwamoto S.Fast transient stability solution using Taylor expansion and energy function[J].Elect.Eng.in Japan, 1985, 105(3): 123-130.

[8]郭志忠.电力网络节点解析新探[D].哈尔滨: 哈尔滨工业大学, 1989.

[9]Xia D Z.On-line transient evaluation by system decomposition aggregation and high order derivatives[J].IEEE Transactions on Power Apparatus and Systems, 1983, 102(7): 2038-2046.

[10]白雪峰, 郭志忠.Taylor级数法暂态稳定计算中阶数的动态控制[J].电力系统自动化, 1999, 23(22):5-7.Bai Xuefeng, Guo Zhizhong.The dynamic control of oder selection in fast transient stability simulation on by higher order Taylor series expansions[J].Automation of Electric Power Systems, 1999, 23(22): 5-7.

[11]毛安家, 郭志忠, 张学松.一种基于广域测量系统过程量测数据的快速暂态稳定预估方法[J].中国电机工程学报, 2006, 26(17): 38-43.Mao Anjia, Guo Zhizhong, Zhang Xuesong.A fast transient stability predicting method based on the WAMS process measurement data[J].Proceedings of the CSEE, 2006, 26(17): 38-43.

[12]岳程燕, 周孝信, 李若梅.电力系统电磁暂态实时仿真中并行算法的研究[J].中国电机工程学报,2004, 24(12): 1-6.Yue Chengyan, Zhou Xiaoxin, Li Ruomei.Study of parallel approaches to power system electromagnetic transient real-time simulation[J].Proceedings of the CSEE, 2004, 24(12): 1-6.

[13]房大中, 张尧, 宋文南.泰勒级数在电力系统暂态稳定性分析中的应用[J].天津大学学报, 1998,31(6): 772-777.Fang Dazhong, Zhang Yao, Song Wennan.Application of Taylor series in power system transient stability assessment[J].Journal of Tianjin University,1998, 31(6): 772-777.

[14]于继来, 郭志忠, 柳焯.基于能量函数高阶 Taylor级数展开技术的直接法[J].电网技术, 1995, 19(2):18-20, 24.Yu Jilai, Guo Zhizhong, Liu Zhuo.Direct method with high order taylor series expansions of energy function[J].Power System Technology, 1995, 19(2):18-20, 24.

[15]汤涌.电力系统稳定计算隐式积分交替求解[J].电网技术, 1997, 21(2): 1-3.Tang Yong.An implicit integration alternating solution method for power system dynamic stability simulation[J].Power System Technology, 1997, 21(2):1-3.

[16]Liniger W, Willoughby R A.Efficient integration methods for stiff systems of ordinary differential equations[J].SIAMJ.1970, 7(l): 47-66.

[17]Johnson R B I, Cory B J, Short M J.A tunable integration method for the simulation of power system dynamics[J].IEEE Transactions on Power System,1988, 3(4): 1530-1537.

[18]容文光, 吴政球, 匡文凯, 等.基于泰勒级数展开的N-1牛顿拉夫逊法快速潮流修正计算[J].电网技术, 2007, 31(2): 42-46.Rong Wenguang, Wu Zhengqiu, Kuang Wenkai, et al.Taylor series expansion based N-1 fast power flow revision calculation using Newton-Raphson method[J].Power System Technology, 2007, 31(2): 42-46.

[19]夏世威, 白雪峰, 陈士麟, 等.多群模式 Taylor级数法暂态稳定计算[J].电力系统自动化, 2010,34(10): 24-28.Xia Shiwei, Bai Xuefeng, Chen Shilin, et al.Transient stability calculation by multi-machine equivalent taylor series method[J].Automation of Electric Power Systems, 2010, 34(10): 24-28.

[20]武和雷, 朱淑云, 胡凌燕, 等.适用于工程应用的Taylor展开系数的求解法[J].南昌大学学报(工科版), 2008, 30(2): 175-178.Wu Helei, Zhu Shuyun, Hu Lingyan, et al.Solutions of Taylor expansion coefficients for engineering application[J].Journal of Nanchang University(Engineering & Technology), 2008, 30(2): 175-178.

[21]郭志忠, 朱文东, 柳焯, 等.电力系统暂态稳定的快速时域仿真判定法[J].电工技术学报, 1994, (03):47-49.Guo Zhizhong, Zhu Wendong, Liu Zhuo.Fast judgment of power system transient stability by time domain simulation[J].Transactions of China Electrotechnical Society, 1994, (03): 47-49.

[22]林济铿, 李杨春, 罗萍萍, 等.波形松弛法的电力系统暂态稳定性并行仿真计算[J].电工技术学报,2006, 21(12): 47-53, 65.Lin Jikeng, Li Yangchun, Luo Pingping, et al.Parallel calculation for power system transient stability based on waveform relaxation method[J].Transactions of China Electrotechnical Society, 2006, 21(12): 47-53,65.

[23]卢锦玲, 朱永利, 赵洪山, 等.提升型贝叶斯分类器在电力系统暂态稳定评估中的应用[J].电工技术学报, 2009, 24(5): 177-182.Lu Jinling, Zhu Yongli, Zhao Hongshan, et al.Power system transient stability assessment based on boosting bayesian classifier[J].Transactions of China Electrotechnical Society, 2009, 24(5): 177-182.

[24]王守相, 张建军.基于统计学习的模糊暂态稳定事故筛选与排序[J].电工技术学报, 2006, 21(3): 112-117.Wang Shouxiang, Zhang Jianjun.Fuzzy contingency filtering and ranking of power system transient stability based on statistical learning[J].Transactions of China Electrotechnical Society, 2006, 21(3):112-117.

[25]李琰, 周孝信, 周京阳, 等.基于引入虚拟负荷的发电机暂态稳定预测[J].电工技术学报, 2008,23(3): 103-107, 130.Li Yan, Zhou Xiaoxin, Zhou Jingyang, et al.The generator transient stability prediction based on additional virtual loads[J].Transactions of China Electrotechnical Society, 2008, 23(3): 103-107, 130.