基于时间域建模的晶闸管调压装置缓冲电路设计

李 凯 袁 峰 丁振良

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

三相晶闸管调压装置被广泛地应用于变载和软起动等对转速指标要求不高的调速场合。在这些场合中，降低整个驱动系统的能量损耗，抑制电流对系统冲击是调速系统设计的目标。实际的电力电子器件并非是理想开关，在换流过程中存在器件损耗，这种损耗还与驱动电路和附加电路有关[1-3]，体现在:①驱动系统与电机之间的长传输线极易造成线路过电压和电压反射现象，抑制此类现象发生有利于降低谐波损耗保证电机系统的可靠运行。②晶闸管的半控特性使得驱动回路只能采取自然换流的工作模式，导致输入触发信号与输出电压之间存在一定时间的延迟，该延迟在晶闸管上产生的积攒电荷在导通瞬间会造成开通损耗，甚至能损坏晶闸管，有效地减少积攒电荷可降低这种损耗。③晶闸管关断瞬间，内部的结电容效应和反向恢复电流作用，会在驱动回路内产生较大幅值的du/dt和di/dt等冲击，这些冲击会造成晶闸管器件损坏和关断损耗。抑制冲击和关断损耗也是研究能耗问题的重点。

目前对第1类问题的研究多采用设计滤波器的方法。对第2类和第3类问题的研究采用设计缓冲电路的方法。RC缓冲电路能提供积攒电荷释放的通道，在大功率柔性输电装置和整流机组的可控串联补偿装置（Thyritor-Controlled Series Compensation,TCSC）上应用广泛，针对晶闸管调压装置的能耗分析和冲击抑制研究较少。本文利用时间域建模方法建立了单相晶闸管在一个工频导通周期内的电阻模型，根据等效电路法获得了不同触发条件下的定子电流，通过电路计算，构建了描述驱动系统能耗的指标函数，定量地将过电压、过电流和电压电流瞬变（du/dt，di/dt）作为方程的约束条件，在约束条件下优化指标函数，获得最佳 RC参数，给出能耗指标优化的结果，仿真曲线验证了抑制冲击的作用，实际的电压波形说明了新方法的有效性。

2 驱动装置模型和定子电流分析

2.1 晶闸管在一个导通周期内的时域模型

依据晶闸管静态伏安特性曲线:在截止区电流几乎为零；当门极电流达到擎柱电流后，晶闸管导通，其正向电阻几乎为零；而当电流小于维持电流后，晶闸管关断，其正向电阻为无穷大。在正弦交流电作用下的一个周波内，晶闸管完成了一个导通周期，按照时间尺度可将晶闸管等效为变化的电阻。

（1）正向截止区[t0，t1）。晶闸管在此区间不导通，处于正向截止状态。实际情况是晶闸管正向有微小的漏电流流过，而且正向电压越大，漏电流越大，其伏安特性表现为极高值电阻。ua为正向电压，ia为正向漏电流，可以用标定的极限情况来确定此区间晶闸管的阻值，如式（1）所示。

式中，Ua为实际正向电压有效值；Ia为实际漏电流有效值；UDRM为正向重复峰值电压有效值；IDRM为正向重复峰值漏电流有效值；RDRM为截止区等效电阻。

（2）正向恢复区[t1，t2）。晶闸管的端电压和电流在此区间都处于由关断向导通的过渡阶段。通态电阻为Ron，可把晶闸管等效成一个指数规律变化的时变电阻，如式（2）所示。

式中，ton为持续时间。

（3）正向导通区[t2，t3）。晶闸管在此区间端电压几乎为零，电流主要由外界负载决定，可用标定的通态平均管压降Uon与平均通态电流Ion之比来等效此阶段的电阻值即Ron，如式（3）所示。

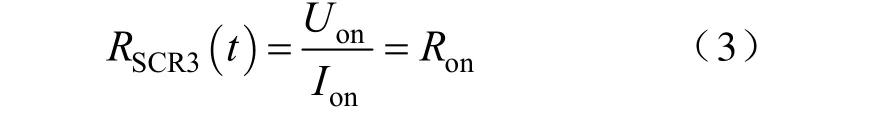
（4）反向导通区[t3，t4）。晶闸管在此区间承受反向电压，由于负载电路中存在电感，因此电流呈现过渡性衰减的状态，其阻断特性尚未恢复，端电压仍为通态电压。可以用平均通态电压和指数变化的电流来表示这一阶段的等效电阻，如式（4）所示。式（4）中，t3为电源正负半周交替时刻，tonr=t4-t3为反向导通区的持续时间。

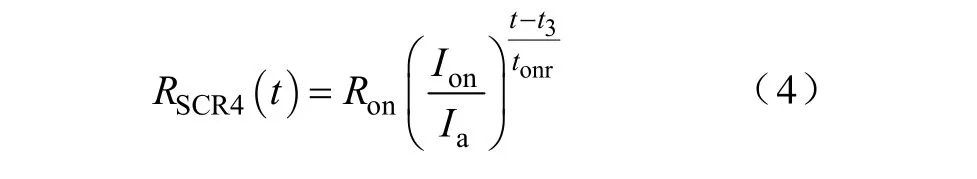
（5）反向恢复区[t4，t5）。晶闸管在此区间 t4时刻电流衰减到零，接着在反方向会流过反向恢复电流，达到反向峰值后，再衰减至零。从正向电流为零，到反向恢复电流衰减至零的时间，就是反向恢复时间。指数函数能够表征晶闸管的变化，如式（5）所示。

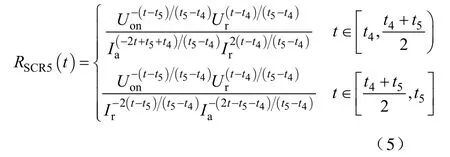
式中，Ir为反向阻断区漏电流有效值；Ur为反向阻断电压有效值。

（6）反向截止区[t5，T）。晶闸管在此区间端电压为实际反向电源电压Ur，电流为反向漏电流Ir，可以等效为反向阻断电阻RRRM，如式（6）所示。

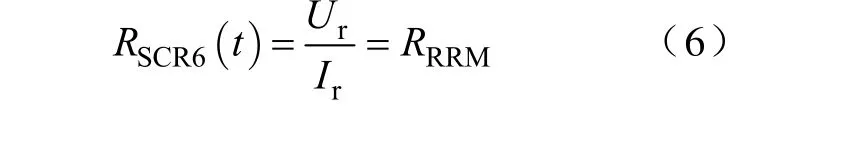
综合式（1）～式（6），统一时间关系，得到晶闸管在一个周期内的时变电阻模型，如式（7）所示。

式中，τ =t-nT，n=[t/T]，[ ]表示向 0方向取整，T为一个周期，即以上6个时间段之和，一个周期内，t0～t5的划分如图1所示。

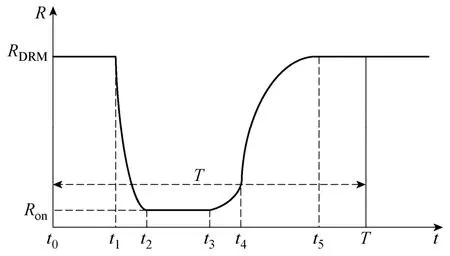
图1 晶闸管在一个交流电周期内的外特性曲线Fig.1 The output characteristics of thyristor in one AC period

2.2 定子电流分析

按照能量等效和绕组归算法则，忽略谐波影响和铁损，感应电机根据Thevenin定理可等效为T型等效电路，单相绕组的等效电路如图2所示。

图2 感应电机单相等效电路Fig.2 Equivalent circuit of single phase IM

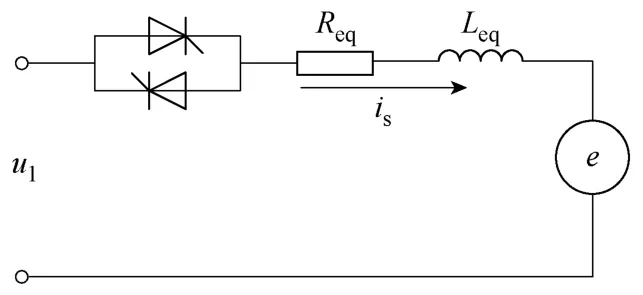
图3 单相晶闸管感应电机电路图Fig.3 Thyristor controlled single phase IM circuit

求解图3所示的电路，得到式（9）和式（10）

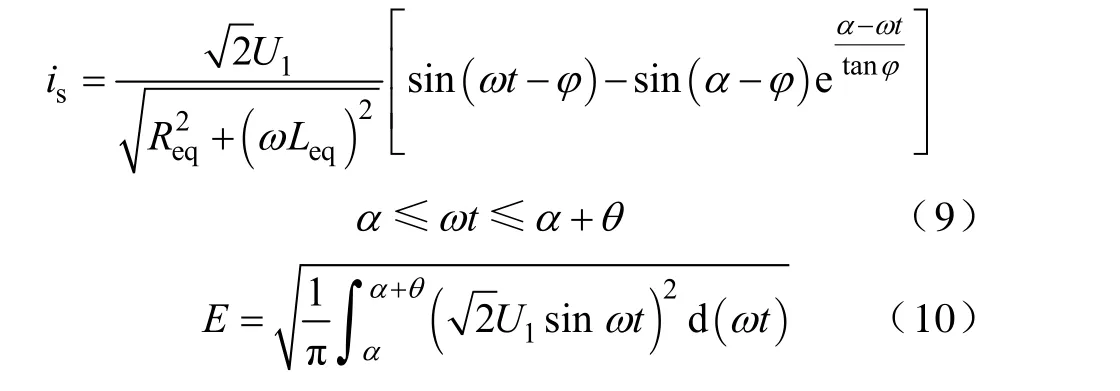
式中，ω=2πf为电源的角频率，φ=arctan（Leq/Req）为等效电路的功率因数角；θ 为晶闸管的导通角；E为反电动势的有效值。

当电源电压 u1的有效值为 220V，电频率为工频50Hz，已知Req=10Ω和Leq=0.3H时，获得不同触发角α对应的定子电流波形如图4所示。

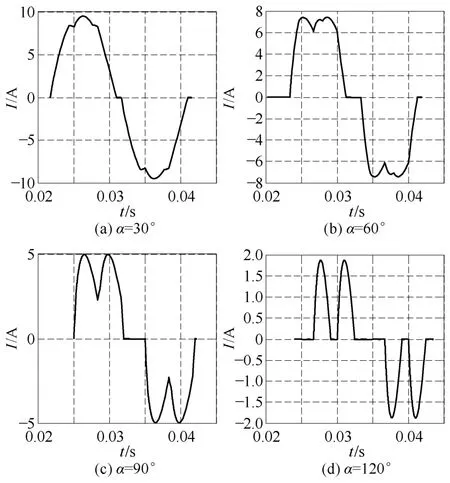
图4 定子电流波形Fig.4 Waveforms of stator current

3 约束条件和性能指标的数学描述

3.1 过压过流冲击的描述

第2节的分析可知:晶闸管可以等效为时变电阻，在门极触发和自然关断的瞬间阻值变化率极大，对应不同α值的定子电流呈现出明显的谐波成分。在电流正向或反向过零瞬间，恰为电流变化率最大时刻，因此畸变往往在此时刻发生。因此，在导通和关断的稳态阶段，求解稳态电路，获得稳态电流；在导通或关断的瞬间，以稳态电流作为初值求解以RC电路和晶闸管等效电阻构成的充放电回路，就可以获得电流过零时刻的特性，从而建立冲击的约束条件。不同状态的电路如图5所示。

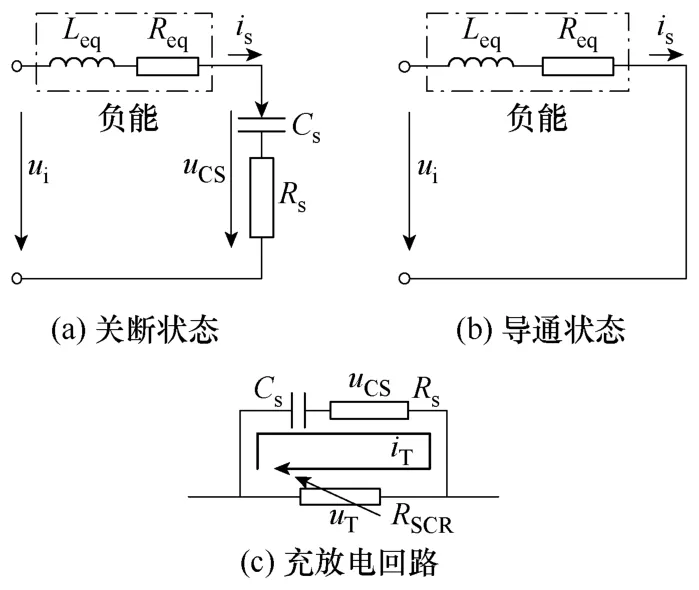
图5 带有缓冲电路的等效电路Fig.5 Equivalent circuit with snubber

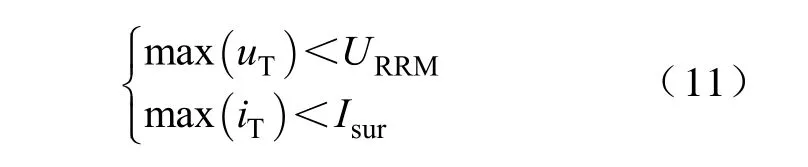
式中，URRM为断态重复峰值电压；Isur为浪涌电流。

3.2 电压电流瞬变的描述

电压电流的瞬变即为极高幅值的 du/dt和 di/dt现象。依据图5，获得电压电流瞬变的描述为

式中，max（duT/dt）和max（diT/dt）分别是电压和电流的最大上升率。

3.3 能耗指标的描述

驱动系统的能耗可以按照定义表示为在一个导通周期内的流经晶闸管的电流与其等效电阻二次方之积的积分，如式（13）所示。

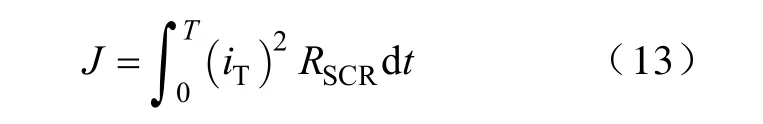
4 带有约束条件的优化问题求解

获得最佳缓冲电路参数的过程可以被理解为通过优化待优化变量对性能指标函数求极值的过程。具体的意义是:优化缓冲电路中的 Rs和 Cs可以描述为:基于图5a和图5b的电路模型，获得is和uCS的时域解析表达式，并以其触发时刻的数值作为图5c电路的初值，在满足式（11）和式（12）的条件下，计算过零点的数值，并求得式（13）的最小值。

4.1 二阶电路的求解

图5a中晶闸管关断时，电路应满足如下方程

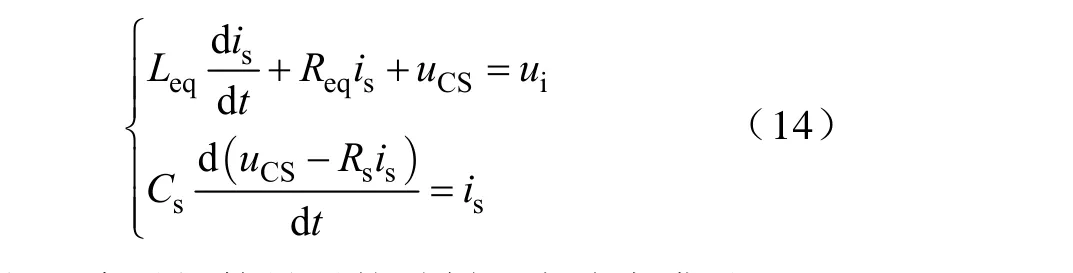
图5b中晶闸管导通的时刻，电路应满足

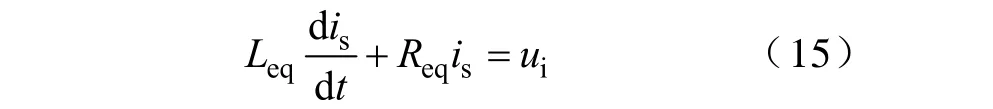
图5c中，充放电回路的电流方程为

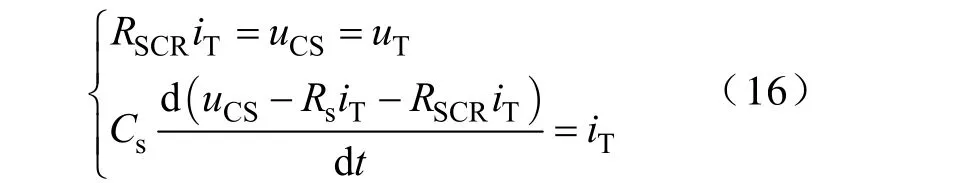
由式（14），当已知参数Req，Leq和ui时，可以获得含有参数 Rs和 Cs的 is时域表达式 is(t)。在 t0时刻晶闸管导通的瞬间有 is(t0)=iT(t0)存在，由此和式（16）可以联立求得充放电过程中晶闸管电流iT(t)。根据式（7），式（11），式（12）和式（13），最终的约束条件和能耗指标如式（17）和式（18）所示。

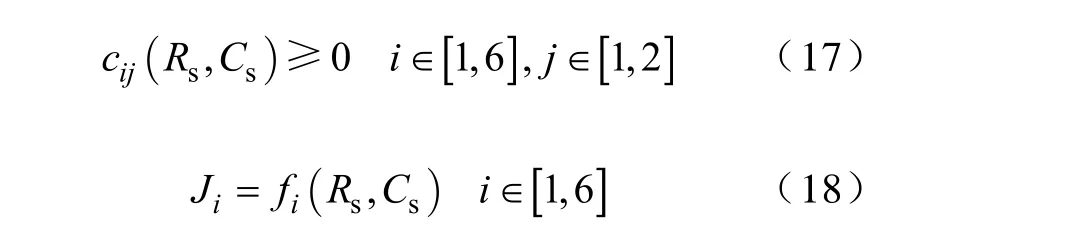
4.2 优化步骤

（1）按时域分段将定积分转为分段积分，如式（19）所示。

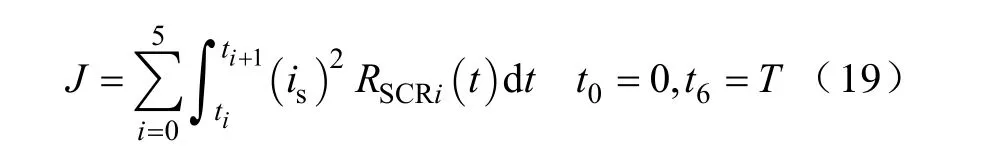
（2）计算每个分段时间域上的能耗Ji。

（3）对每个分段上的 Ji与约束条件 cij转化为Lagrange函数，如式（20）所示。

式中，x=(Rs,Cs)T。

（4）根据Fritz-John条件计算最优点，所得结果为这个区间上基于时间域建模法的缓冲电路参数。

（5）选取对应能耗指标最小的参数作为最终结果。

4.3 计算结果

电机等效电路的参数为:Req=3.115Ω，Leq=0.1811H。晶闸管（型号KP—200）的参数:URRM=UDRM=1600V，UTM=1.3V，IRRM=IDRM=15mA，ITM=200A。一个周期内的优化结果如表所示。

表 一个周期内的优化结果Tab The optimized solution in one period

由表得知:①在不同的时间区间内最小能耗对应的最佳参数匹配不一致，只能兼顾各个区间段的优化结果并选择折中的参数；②在反向恢复区最小能耗指标较大，此时缓冲电容较小时可以避免关断造成的冲击；③在正反向截止区最小能耗指标较小，此时缓冲电阻较小时能够抑制开通损耗。综合上述分析，最终确定Rs=10Ω，Cs=0.47μF。

4.4 仿真曲线和实际波形

图6的仿真条件为:交流电源电压有效值为220V，频率为 50Hz，触发角 30°，电流波形带有25A的限幅。电机参数和缓冲电路参数如 4.3节所示。图6a的仿真曲线未施加缓冲电路，图6b的仿真曲线施加了缓冲电路。从中可以明显看出缓冲电路能够有效地抑制过电流和电流突变。图7的仿真条件同图 6，只是触发角不同。仿真曲线表明:驱动装置能耗主要发生在反向恢复阶段，缓冲电路参数抑制能耗的作用不随触发角的变化而变化。

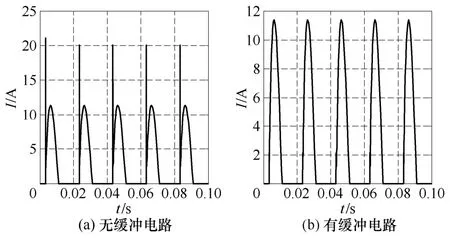
图6 晶闸管电流仿真曲线Fig.6 Current simulation curves of thyristor

在具体实验中，我们依据此方法设计了最优的缓冲电路参数，得到了如图8所示的实际电压波形。图8中上半部分为电源电压，下半部分为晶闸管输出电压，实验参数同4.3节，触发角为60°。两个波形的对比可以看出，过电压和较大幅值的 du/dt已经明显被抑制，在反向恢复区没有出现较大幅值的反向电压，这表明驱动系统的能耗抑制比较明显。

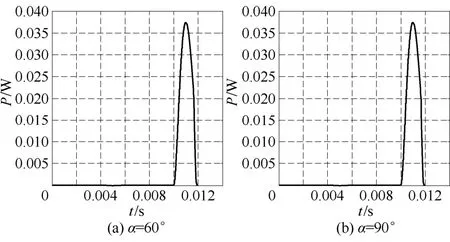
图7 晶闸管功耗仿真曲线Fig.7 Power loss simulation curves of thyristor

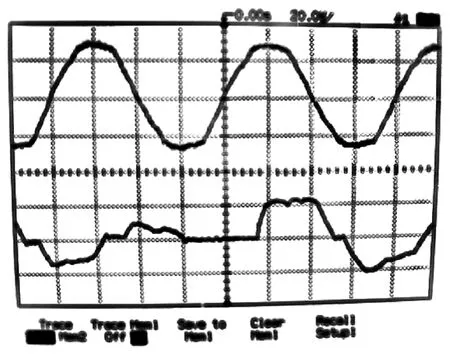
图8 带有缓冲电路的晶闸管电压实际曲线Fig.8 Actual thyristor voltage curves with snubber circuit

5 结论

本文以三相晶闸管调压驱动装置作为研究对象，为了解决驱动装置功耗和冲击抑制问题，采用时间域的建模方法构建了在一个导通周期内的等效电阻，并描述了能耗指标函数和冲击的约束条件。提出了优化带有约束的能耗指标，从而获得最佳缓冲电路参数配置的思想。并通过仿真和实验进行了验证。在构建能耗指标函数和系统冲击的约束条件时，只利用了求导的手段，而且对指标函数的参数化求解较为烦琐。文中的建模和优化基于电机的稳态参数。对应不同时间常数的参数变化对优化结果的影响没有考虑，上述问题值得进一步去讨论研究。

[1]蓝元良, 汤广福, 印永华.串联晶闸管反向恢复暂态过程研究[J].电网技术, 2006, 30(16): 15-19.Lan Yuanliang, Tang Guangfu, Yin Yonghua.Study on transient of reverse recovery of series thyristors[J].Power System Technology, 2006, 30(16): 15-19.

[2]王毅, 石新春, 李和明, 等.基于统一离散时域建模法的晶闸管串联运行暂态仿真[J].电力系统自动化, 2004, 28(18): 41-44.Wang Yi, Shi Xinchun, Li Heming, et al.Cascaded thyristors simulation based on unified discrete time-domain modeling[J].Automation of Electric Power Systems, 2004, 28(18): 41-44.

[3]Minseok Joo.Losses of thyristor on modified bridge type high-temperature superconducting fault current limiter[J].IEEE Transactions on Applied Superconductivity, 2004, 14(2): 835-838.

[4]王榕生.基于交流电机负载双向晶闸管关断电压暂态研究及缓冲电路参数优化[J].福州大学学报,2007, 35(2): 234-240.Wang Rongsheng.A study of transient state on triac off-state voltage and optimization of parameters of snubber circuit for 3-phase induction motors switching application[J]. Journal of Fuzhou University, 2007, 35(2): 234-240.

[5]张冬霞, 童陆园, 尹忠东, 等.描述可控串补装置暂态特性的数学模型[J].中国电机工程学报, 1999,19(5): 30-34.Zhang Dongxia, Tong Luyuan, Yin Zhongdong, et al.Analytical mathematical model for describing the dynamic behavior of the thyristor controlled series compensator[J].Proceedings of the CSEE, 1999,19(5): 30-34.

[6]葛俊, 童陆园, 耿俊成.基于电容电压同步下TCSC暂态特性的数学描述[J].中国电机工程学报, 2001,21(3): 1-5.Ge Jun, Tong Luyuan, Geng Juncheng.The mathematical model for describing transient characteristics of TCSC based on capacitor voltage synchronization mode[J].Proceedings of the CSEE,2001, 21(3): 1-5.

[7]Donlon John F, Motto Eric R, Yamamoto M, et al.A new gate commutated turn-off thyristor and companion diode for high power applications[C].Proceedings fo the IEEE Industry Applications Society Annual Meeting, 1998: 1-8.

[8]Cardoso Filho Braz J, Lipo Thomas A.Application of MTO-thyristors in current stiff converters with resonant snubbers[C].Proceedings fo the IEEE Industry Applications Conference, 1999: 1-8.

[9]Astrom U, Danielsson B, Nyberg K.Alternative solutions for thyristor control and gating for HVDC-valves[C].Proceedings fo the IEEE Power System Technology 1998: 1-4.

[10]汤涌.交直流电力系统多时间尺度全过程仿真和建模研究新进展[J].电网技术, 2009, 33(16):1-8.Tang Yong.New progress in research on multi-time scale unified simulation and modeling for AC/DC power systems[J].Power System Technology, 2009,33(16):1-8.