基于Tow-Thomas二阶节的椭圆低通滤波器的设计
2012-08-01任青莲高文华
任青莲,高文华
(太原科技大学电子信息工程学院,太原030024)
滤波器具有选频、滤波的功能,是去除信号中干扰和噪声的基本手段,在通信、电子工程和信号处理等领域起着非常重要的作用。椭圆滤波器以其通带纹波小、阻带衰减大、过渡带宽窄、所需阶数少等优良特性而著称,广泛用于幅频特性要求苛刻的场合。而椭圆函数是一种较复杂的逼近函数,当需要用椭圆函数对滤波网络进行综合设计时,用传统的方法要进行复杂的计算,还要根据计算结果进行查表,得出所需滤波器的阶数和归一化的零、极点,再用频率标度系数将零、极点去归一化,整个过程比较繁琐而且存在较大的困难[1-5]。
利用MATLAB提供的丰富的模拟滤波器设计函数,根据设计指标,通过编程,可以很便捷地求出所需椭圆滤波器的阶数和零、极点的位置,大大简化了椭圆滤波器的设计过程[1-2]。使用Tow-Thomas二阶节电路结构作为椭圆低通滤波器的核心单元,不仅使设计适用于多种不同的滤波要求,而且极大地方便了滤波器的通带增益、品质因数及截止频率等参数的调整[6-8]。
1 椭圆低通滤波器
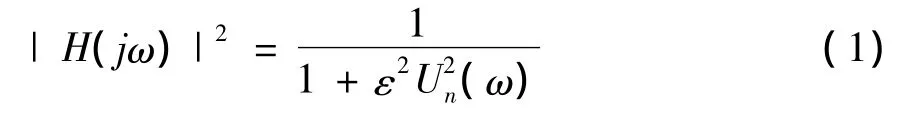
式中:n为滤波器的阶数,由式(2)计算(或查相关设计手册中图表数据得出),ε为纹波系数,Un(ω)为n阶Jacobi椭圆函数。
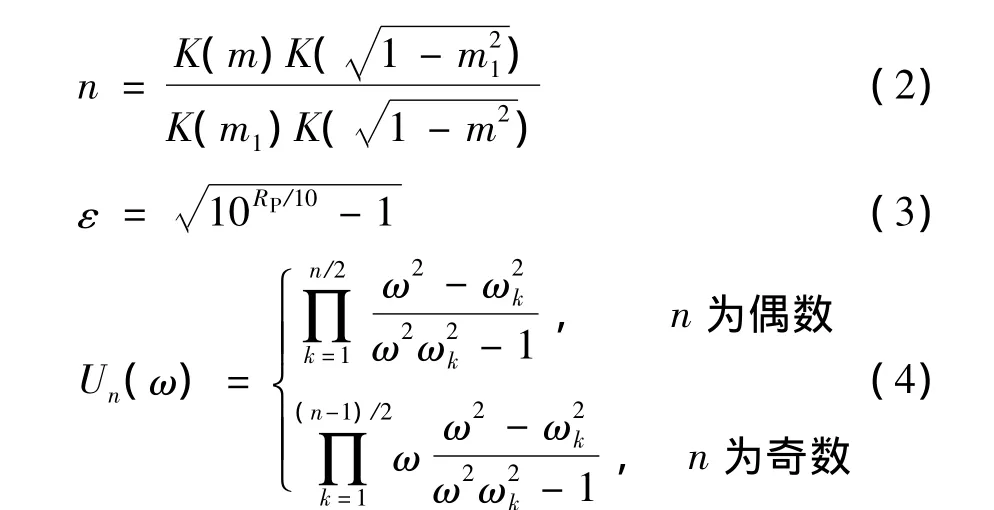
根据设计指标,包括:通带允许波动的最大值Rp和阻带衰减的最小值As,以及相应的通带截止频率ωp和阻带截止频率ωs,利用MATLAT提供的函数编程,求得滤波器所需的阶数n,数值传递函数的虚数零点(0,±ωk∞)以及复数极点(-αk,±βk),若滤波器的阶数为奇数,还包括实极点(-α0,0)。则可得滤波器的数值传递函数:
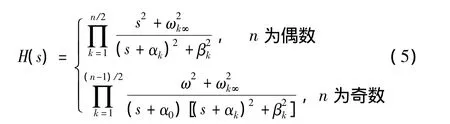
以上所得滤波器的传递函数为高阶多项式,采用把高Q值的极点与离该极点最近的零点配对的原则,可将其分解成若干一阶函数与二阶多项式的乘积,所以高阶滤波器可用级联法实现。如果滤波器阶数是偶数,那么该滤波器可以由多个二阶滤波器级联而成;如果滤波器阶数是奇数,那么滤波器可由一个一阶滤波器与多个二阶滤波器级联构成。级联设计的关键是二阶基本节的设计。
2 Tow-Thomas二阶节低通滤波器
最常用的二阶节电路结构有Sallen-Key与Tow-Thomas,Sallen-Key结构只需要一个运算放大器便可实现一个二阶函数,然而其容易受到寄生参数的影响,灵敏度太高,只适用于Q值比较低的滤波器的应用。相对于Sallen-Key滤波器,Tow-Thomas滤波器虽然需要多个运算放大器,但是其具有相对较低灵敏度,其最重要的特点是,可以通过调节电路中各元件的值来独立调节滤波器的通带增益、品质因数及截止频率等参数,大大简化了调谐的工作,因此被广泛应用于各种电路中。
具有传输零点的Tow-Thomas二阶节电路结构如图1所示。
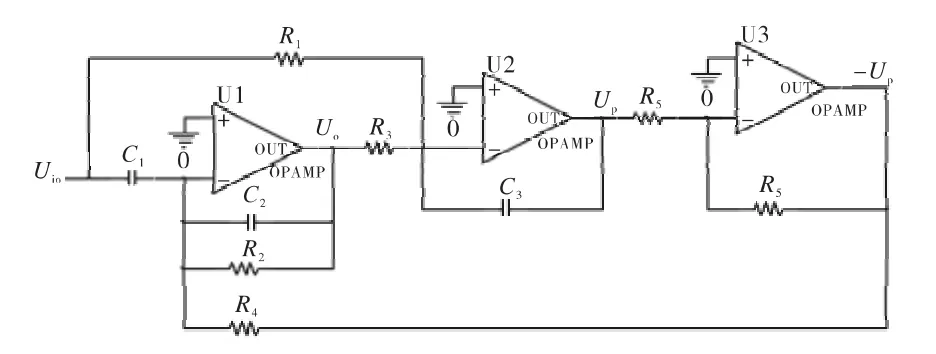
图1 具有传输零点的Tow-Thomas二阶节电路结构Fig.1 Tow-Thomas biquad with transmission zeros circuit
对电路列出方程式:
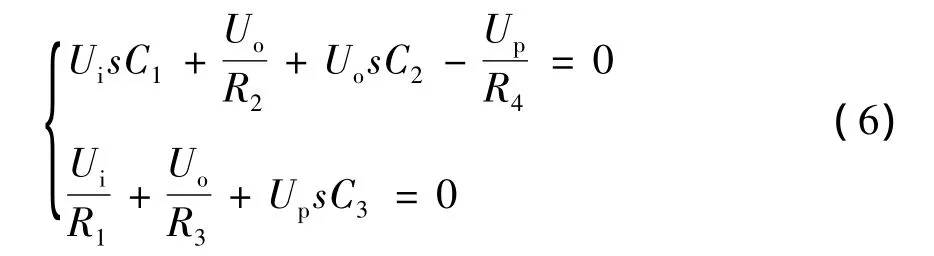
解联立方程组,可以得到电路的传递函数为:
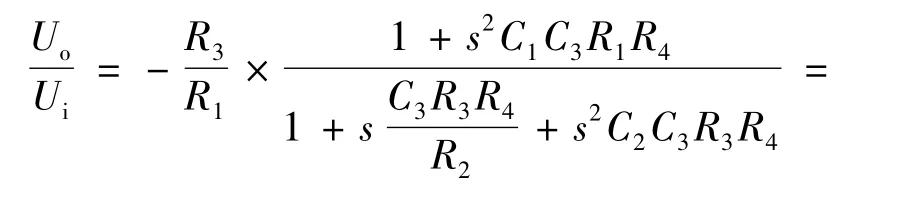

则可得电路的符号传递函数为:
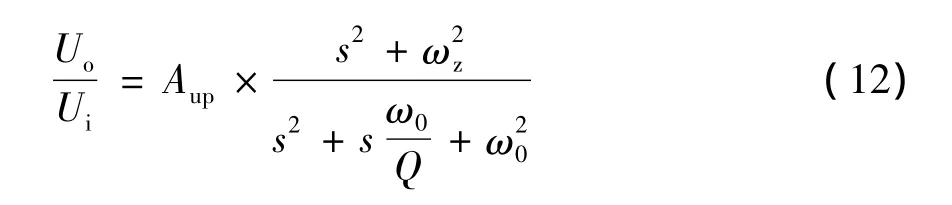
由式(12)可知,该二阶节提供了一对虚数零点和一对共轭复节点。与式(5)的数值传递函数对应,有以下关系:
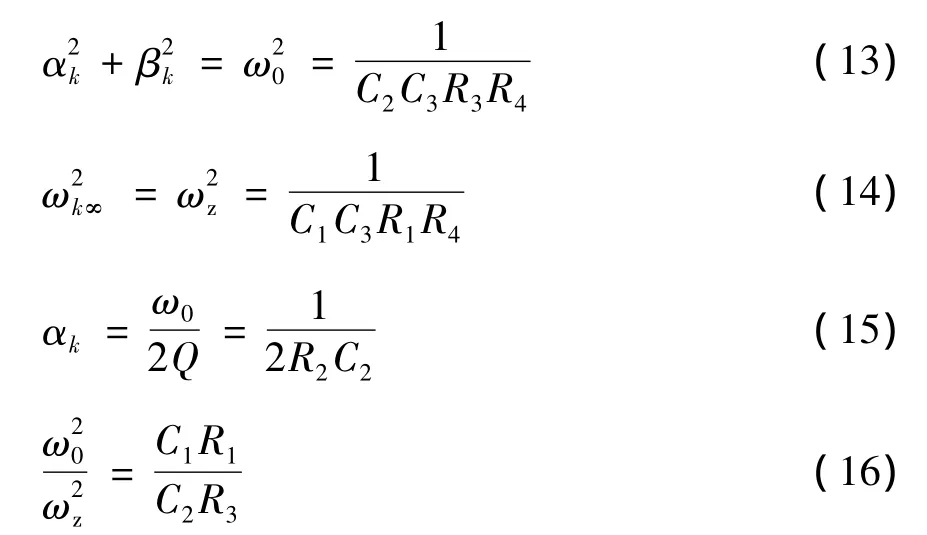
选取标称电容C和电阻R,令R1=R3=R,C2=C3=C,则得:
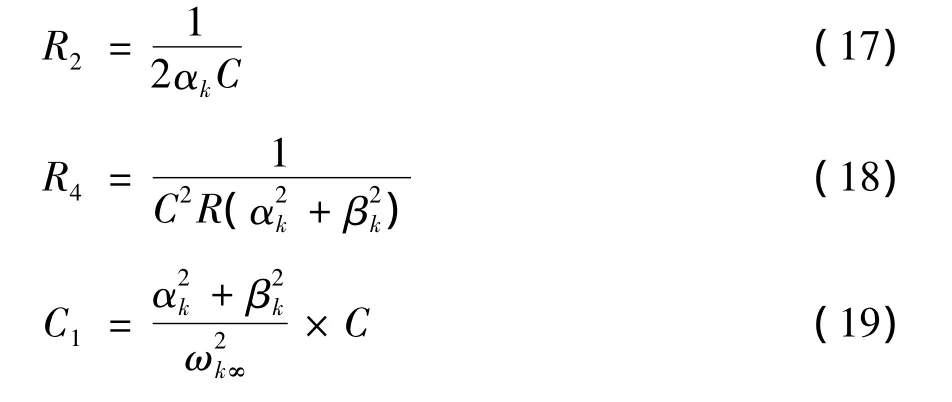
若有实数极点,在输入端加一阶有源滤波电路,如图2所示,取R0=R,C0由实数极点α0确定:

3 设计实例分析
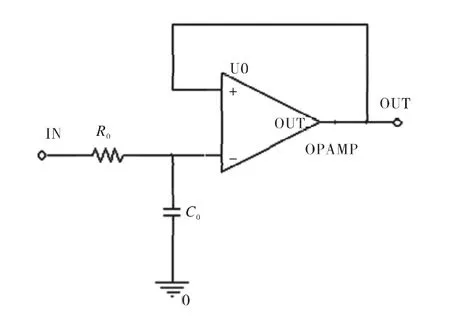
图2 一阶有源低通滤波器Fig.2 One step active low-pass filter
设计一椭圆低通滤波器,要求通带截止频率为6 kHz,阻带截止频率为 7.5 kHz,通带允许波动的最大值为0.28 dB,阻带衰减的最小值为35 dB.
调用MATLAB ellipord函数,确定所需阶数和带宽,程序代码如下:
Wp=6000*2*pi; %通带截止角频率
Ws=7500*2*pi; %阻带截止角频率
Rp=0.28; %通带纹波
Rs=35; %阻带最小衰减
[n,Wn]=ellipord(Wp,Ws,Rp,Rs,'s'),%n 为滤波器的最小阶数;Wn为滤波器的通带宽度。
计算结果为 n=5,Wn=37 699 kHz.
根据计算的滤波器的最小阶数n,调用MATLAB ellip函数求解滤波器的数值传递函数,确定零、极点,绘出滤波器零、极点图和滤波器幅频相应,程序代码如下:
[B,A]=ellip(N,Rp,Rs,Wn,'s');%B 为 H(s)的分子多项式系数;A为H(s)的分母多项式系数;
z=roots(B) %求解H(s)的零点;
p=roots(A) %求解H(s)的极点;
pzmap(p,z) %绘制系统的零、极点图;
W=linspace(100,9000,4000)*2*pi;
H=freqs(B,A,W);%幅频响应;
magH=abs(H);
plot(W/(2*pi),20*log10(magH));
得滤波器的虚数零点坐标(0,±ωk∞)分别为(0,±67 670)、(0,±47 848);复数极点坐标(-αk,±βk)分别为(-2 636,±38 673)、(-11 875,±29 894);实数极点坐标(- α0,0)为(-21 696,0).
零、极点图如图3所示,幅频特性如图4所示。由图4可知,该滤波器满足各项指标要求。
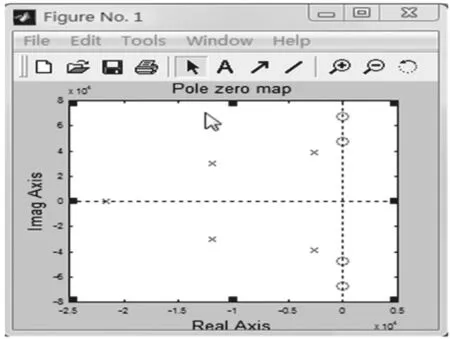
图3 零、极点图Fig.3 Zero,pole diagram

图4 滤波器的幅频特性Fig.4 The frequency characteristics of filter
在图3中,采用把高Q值的极点与离该极点最近的零点配对的原则,分配零、极点到每一节中,实极点分配到一阶滤波电路中。分A、B、C三节,如图5所示。其中A节包含实极点(-21 696,0),B节包含零点(0,±47 848)和复数极点(-2 636,±38 673),C节包含零点(0,±67 670)和复数极点(-11 875,±29 894)。
选择 R1=R3=R5=5.1 kΩ,C2=C3=0.01 μF,根据式(13)到式(20)利用MATLAB编写程序计算出各元件值,如表1所示。
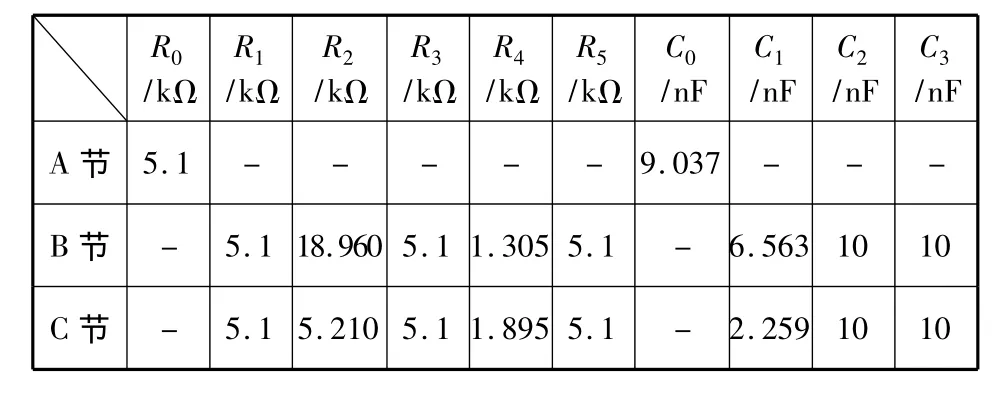
表1 各滤波节电阻与电容的计算值Tab.1 Each filter section resistance and capacitance calculation
根据表1计算所得的各元件值,利用Orcad10.5绘制电路图,如图5所示,调用Pspice10.5进行电路仿真,其幅频特性如图6所示,由仿真结果可知:带内衰减最大为0.28 dB,3 dB截止频率为6.23 kHz,在 7.5 kHz处的衰减为 40 dB,8.5 kHz时的衰减为35 dB,完全满足设计要求。
在实际调试时,可以通过调节各节的R2来改变滤波器的Q值,调整R1来获得不同的增益要求,调整C1的值来改变陷波点的位置。

图5 滤波器设计电路图Fig.5 The circuit diagram of filter
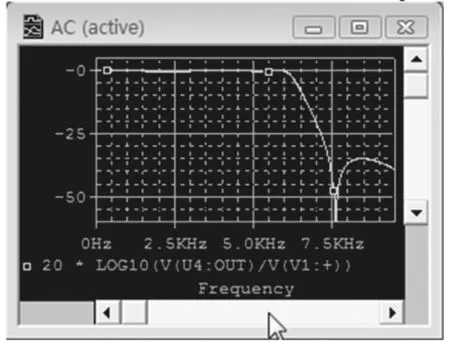
图6 滤波电路的仿真结果Fig.6 Filter simulation results
4 结论
根据给定的技术指标,利用MATLAB求出椭圆滤波器的零、极点,得出滤波器的数值传递函数,根据零、极点图进行零、极点配对,再与Tow-Thomas二阶节的符号传递函数对照,综合计算出电路的各元件值,最后,利用电路仿真软件Orcad/Pspice10.5对电路进行仿真分析,所得结果完全能满足设计要求。由于Tom-Thomas电路具有调整独立,制作方便的特点,因此,本文给出的方法具有一定的应用价值。
[1]肖有平,胡霞.高阶椭圆滤波器的设计与仿真[J].电子测量技术,2007,30(3):147-150.
[2]王田,CELESTINO A CORRAL.椭圆滤波器边带优化设计方法研究[J].仪器仪表学报,2005,26(6):562-565.
[3]滕建辅.用Tow-Thomas电路设计Bessel带通滤波器的方法[J].天津商学院学报,2005,25(3):1-3.
[4]赵建珍,董增寿.改进的自适应均值滤波算法及应用[J].太原科技大学学报,2010,31(1):34-37.
[5]韩建宁,韩如成,智泽英.一种快速自适应谐波检测的APF仿真研究[J].太原科技大学学报,2008(4):253-257.
[6]周明兴.CMMB调谐器中滤波器的设计[D].上海:上海交通大学,2010.
[7]滕颖.单片全集成 RC有源滤波器的设计[D].天津:天津大学,2007.
[8]王英.带有传输零点的集成有源滤波器设计[D].天津:天津大学,2008.
