铸态2.25Cr1Mo0.25V钢的高温热变形行为

焦永振，安红萍，刘建生

(太原科技大学材料科学与工程学院，太原030024)

随着石油冶炼技术的发展，加氢反应器作为炼油工业中的重要部件向着设备大型化、高性能的趋势发展。2.25Cr1Mo0.25V钢以其更高强度、良好的抗高温回火脆性及优越的抗堆焊层氢剥离性迅速成为了制造加氢反应器的首选材料[1]。目前，国内对该钢也做了些研究[2-5]，他们研究了锻态下的组织、性能、工艺热变形行为。但对铸态2.25Cr1Mo0.25V钢的热变行为涉及相对较少。在热变形过程中，形变温度、应变速率和流变应力等热力学参数都会影响材料的热变形力学行为，而材料的热变形力学行为，又是衡量材料塑性加工性能的一个重要指标。本工作研究了2.25Cr1Mo0.25V钢在铸态下的热变形行为，分析在热压缩过程中热力学参数之间的关系，为相关的数值模拟提供数据基础。

1 试验方法与过程

本次试验所用材料为中国二重冶炼的234t大型2.25Cr1Mo0.25V铸态钢锭，取样位置位于锭身处距冒口1 400 mm处，从钢锭中心部位，沿半径方向由内而外的等轴晶区内，其化学成分如下表所示:

表1 2.25Cr1Mo0.25V钢的化学成分(%，质量分数)Tab.1.Chemical compositions of 2.25Cr1Mo0.25V steel in wt%

将取下的材料制成尺寸为Ø8×12 mm的圆柱体试样，采用Gleeble-1 500D热模拟试验机做热压缩试验，形变温度分别为950℃，1 050℃，1 150℃，1 250 ℃，应变速率分别为 0.005 S-1，0.01 S-1，0.1 S-1，真应变为 0.5，试验流程如图所示(图 1)。

试样高温变形后，应立即进行急冷，使其保留高温形变结束时的组织。将热压缩变形后的试样，采用线切割机床沿轴线方向剖开后，进行磨制、抛光，用加洗洁精的过饱和苦味酸溶液在40℃的温度下进行腐蚀，并采用ZAISS Imager.A1m光学显微镜观察组织，用截线法测量观察到的晶粒尺寸，测定晶粒个数不少于300个。

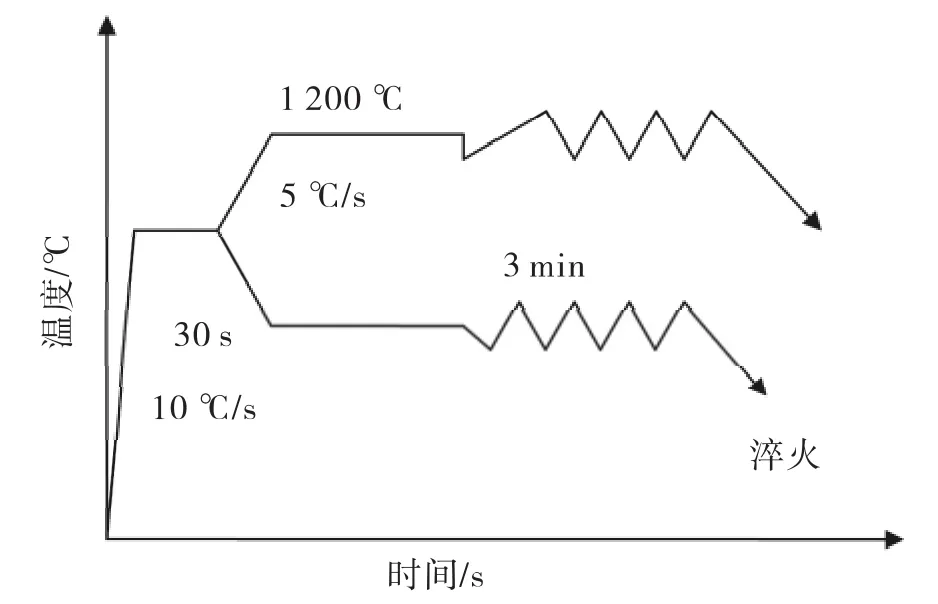
图1 实验流程图Fig.1 The experiment procedure

2 试验结果与分析

2.1 不同形变参数下的真应力-应变曲线图

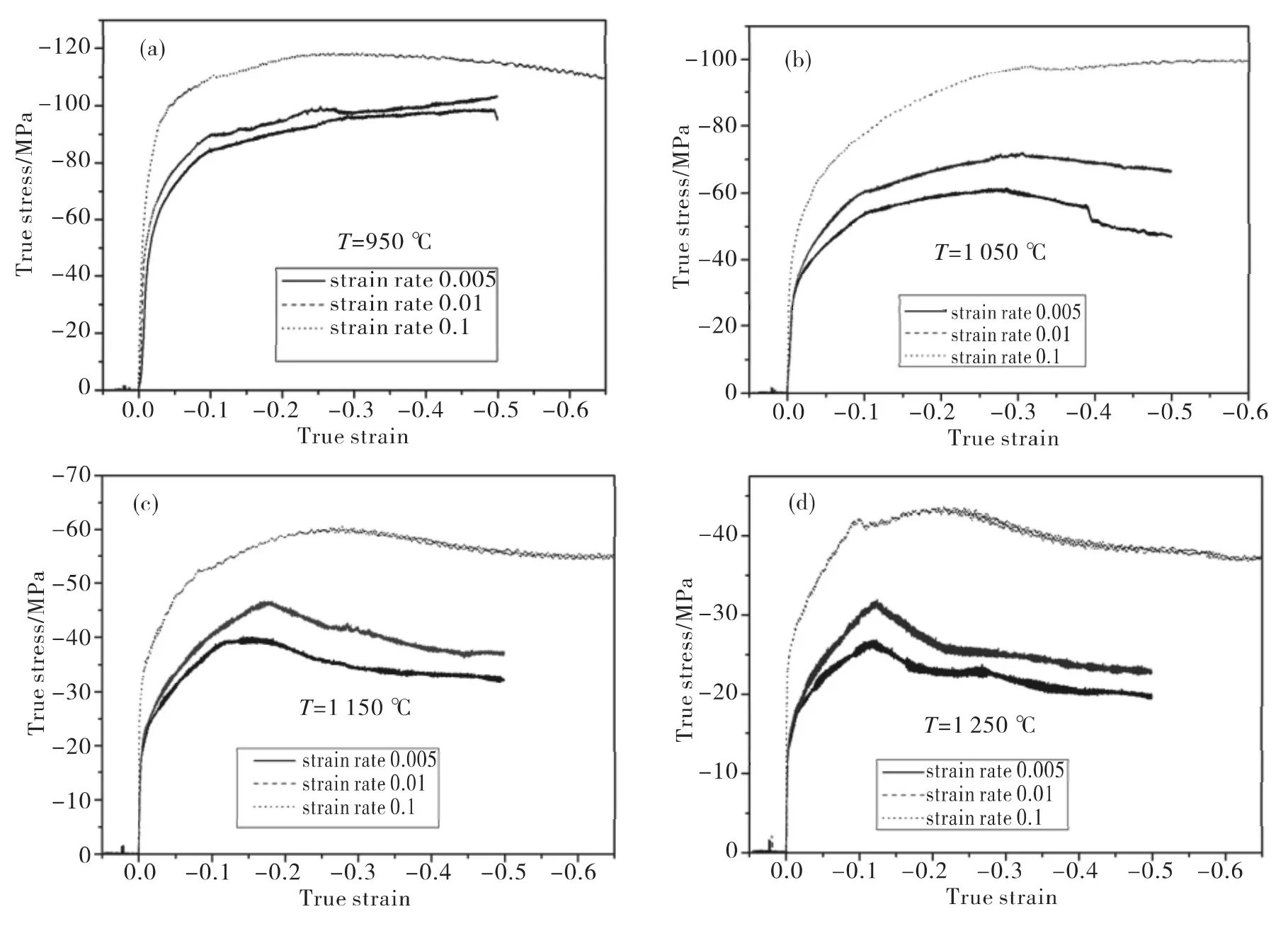
图2 不同变形条件下的真应力-真应变曲线Fig.2 True stress-true strain curves under different deformation conditions

图2是最大变形量为40%时，在不同的温度和应变速率下的真应力-应变图。从图中可以看出，应力应变曲线的类型包括，加工硬化型曲线、动态回复型曲线和动态再结晶曲线。在温度较低，应变速率较大的条件下，真应力应变曲线呈动态回复型;在温度较高，应变速率较低的条件下，真应力应变曲线呈现动态再结晶型。

温度为950℃，应变速率为0.005 S-1和0.01 S-1条件下的应力应变曲线的特征为，流变应力随着应变值的增加而增大，符合属于加工硬化型应力应变曲线的变化规律。温度为950℃，应变速率为0.1 S-1和1 050℃各个应变速率条件下的曲线特征为，其流变应力随应变的增大而增大，当达到某个定值时逐渐趋于稳定状态，符合动态回复型曲线的变化规律。在温度为1 150℃和1 250℃的条件下，各应变速率下的曲线的特征为，流变应力先增大到一个峰值，然后随应变的增加，流变应力有所降低，降低到某一定值后进入一个稳态的平衡阶段，该特征符合动态再结晶类型曲线的变化规律。

从应力-应变曲线图2中可以看出，在温度和应变量相同的条件下，应变速率越低，峰值应力越小，峰值应变越小。如在温度为1 050℃，应变速率为0.1S-1条件下的峰值应力为 100.12 MPa，应变速率为 0.01 S-1条件下的峰值应力为 72.028 MPa，应变速率为0.005 S-1条件下的峰值应力为61.357 MPa.由于应变速率较低时，动态再结晶容易发生，抵消了加工硬化作用，使得材料的流变应力降低。随着应变速率的提高，峰值应力和应变会随之增大，动态再结晶会变得困难。由于应变速率的增加，峰值应力增大，导致变形抗力增大，不利于动态再结晶的进行，因此在该条件下加工硬化在热压缩过程中占主导地位，致使流变应力增大。

在应变速率和应变量相同的条件下，材料的流变应力、峰值应力和峰值应变均随着形变温度的升高而呈现降低的势态。如在应变速率为0.005 S-1，温度为950℃的条件下，峰值应力为98.892 MPa，温度为1 050℃的条件下，峰值应力为61.357 MPa，温度为1 150℃的条件下，峰值应力为40.023 MPa，温度为1 250℃的条件下，峰值应力为26.815 MPa。由于当形变温度较低时，能量较低，无法使位错产生攀移和交滑移，此时加工硬化率大于动态再结晶和回复的软化速率，该阶段主要发生加工硬化。随着温度升高，原子运动能力增强，空位密度增大，位错运动的驱动力增大，动态再结晶会很容易发生。动态再结晶会完全或部分消除了加工硬化效果，使流变应力逐渐降低。曲线的峰值应变也随温度的升高而减小，较流变应力与峰值应力而言相对缓慢，受温度影响较弱。

2.2 高温热变形本构方程和形变激活能的确定

热变形激活能是发生动态回复和动态再结晶的动力，其大小决定了变形过程中的动态回复和动态再结晶发生的情况。Arrhenius方程包含了变形激活能Q、温度T和应变速率˙ε之间的关系[3-6]。

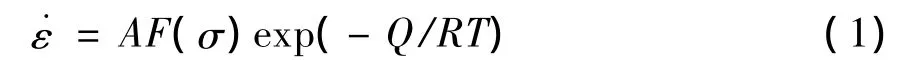
其中，F(σ)有三种形式，当应力较低时，即:ασ ＜ 0.8时，F(σ)= σn1;

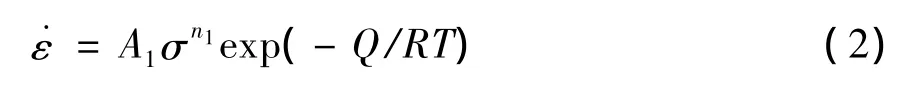
当应力较高时，即ασ ＞ 1.2时，F(σ)=exp(βσ)

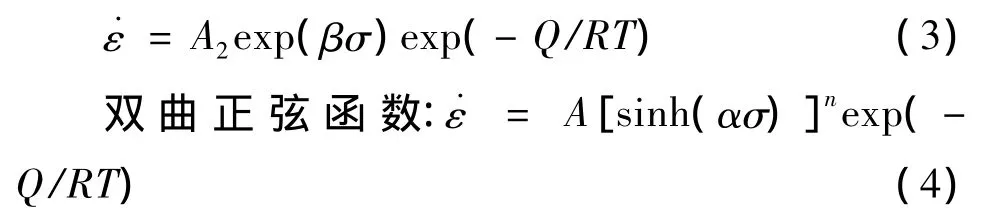
双曲正弦函数适用于不同温度、应变率和应变下的应力;式中:˙ε为应变速率(s-1);R为气体常数(8.31 J/mol·K);T为绝对温度(K);Q为形变激活能(kJ/mol);σ 取峰值应力 σp(MPa);A，A1，A2，α，n和n1为材料常数，其中α=β/n1.

对式(1)和(2)，两边求对数得:

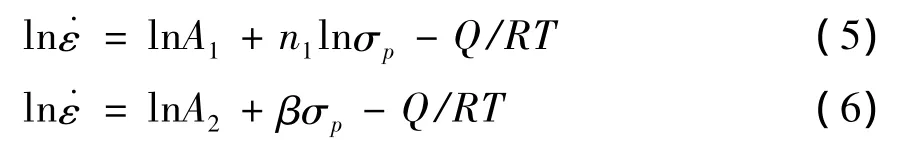
当形变温度相同时，上式中的lnA1、lnA2和Q/RT均为常数。分别绘制lnσp、σp和ln˙ε的关系图(图3、图4)。线性回归得出不同温度下的斜率，对其倒数求平均值得出n1=9.267 32;采用相同方法可求出 β =0.141 19，则 α = β/n1=0.015 2.

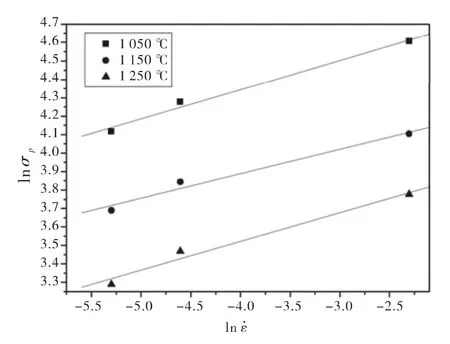
图3 lnσp与ln˙ε的关系Fig.3 Relationship between lnσpand ln˙ε

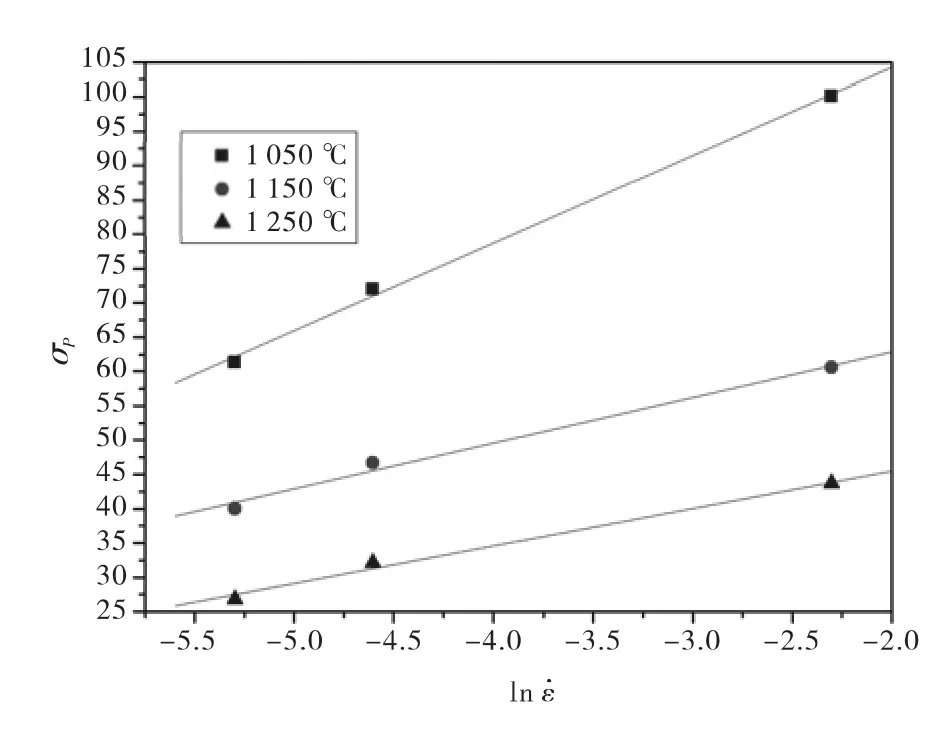
图4 σp与ln的关系Fig.4 Relationship betweenσpand ln

对(4)式，两边取对数得:

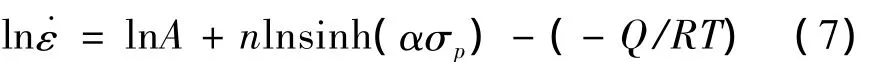
并对式(7)进行偏微分，得出形变激活能的Q的表达式:

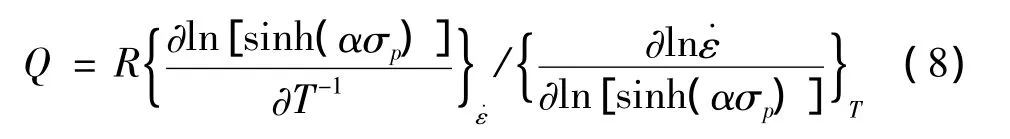
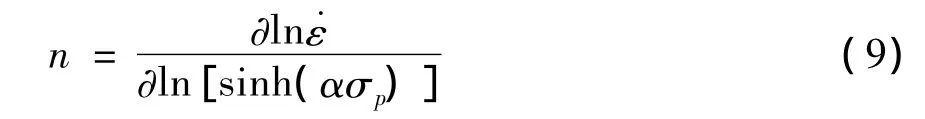
当温度不变时，n的求解关系式可表示为:

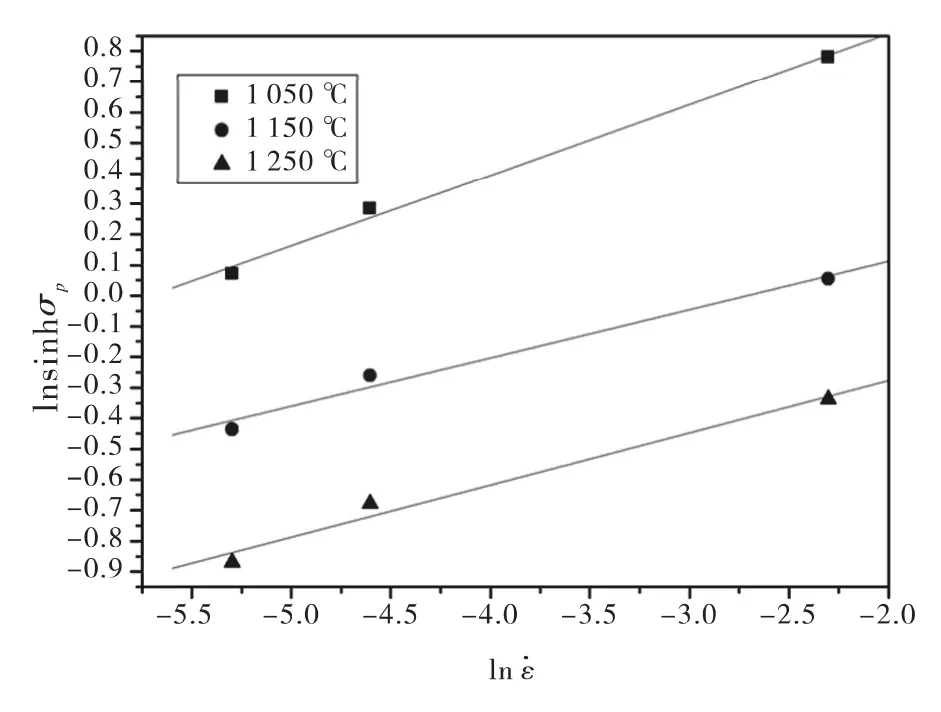
图5 ln[sinh(ασp)]与ln的关系Fig.5 Relationship between ln[sinh(ασp)]and ln

当应变速率不变时，形变激活能的关系式可表示为:

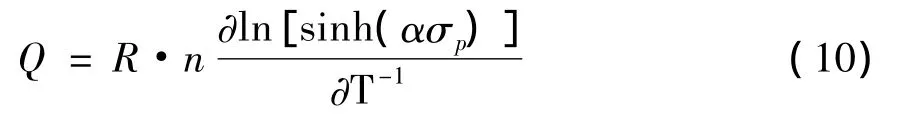
对ln[sinh(ασp)]和10 000/T的关系作图6，可得出平均值为0.61，将上述拟合出的数值带入Q的表达式:Q=R·n × 0.61=305.312 kJ/mol.

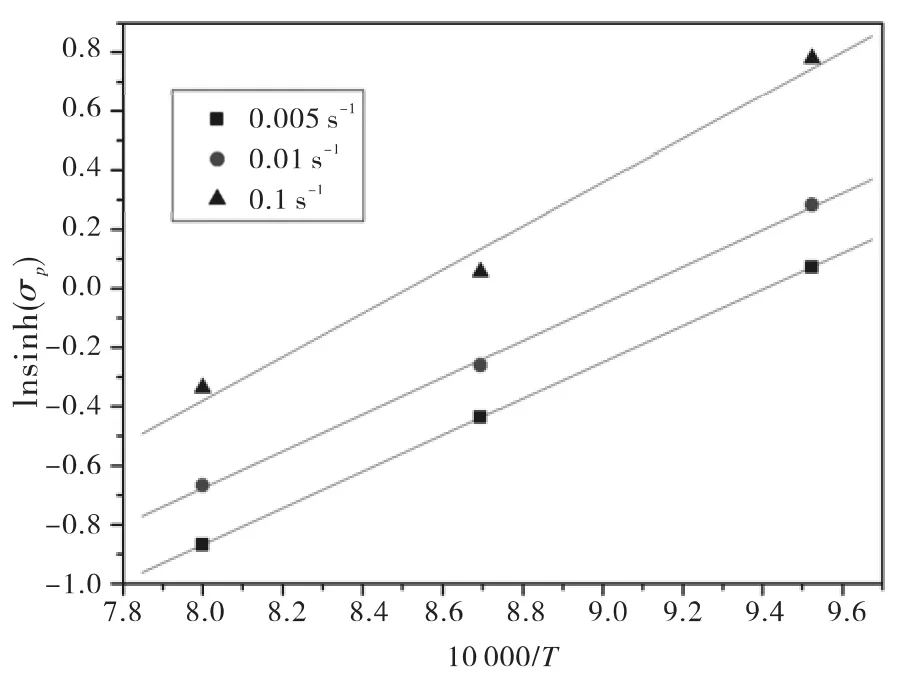
图6 ln[sinh(ασp)]与温度T的关系Fig.6.Relationship between ln[sinh(ασp)]and temperature

高温塑性本构关系体现了流变应力、形变温度和应变速率等变形过程中热力学参数之间的关系。Zener和Hollomon在1944年研究钢的应力-应变关系时发现，他们取决于应变速率和形变温度T，其关系可以用Zener-Hollomon参数来表示[7]:

式中Z是Zener-Hollomon参数，是用温度补偿了应变速率，Q为形变激活能，引入双曲正弦函数可得:

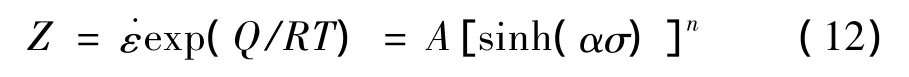
将求得的Q值、温度、应变速率及其它参数带入式(11)中，在得到lnZ值后，对式(12)两端求对数，并对 lnZ-ln[sinh(ασp)]作关系图7.

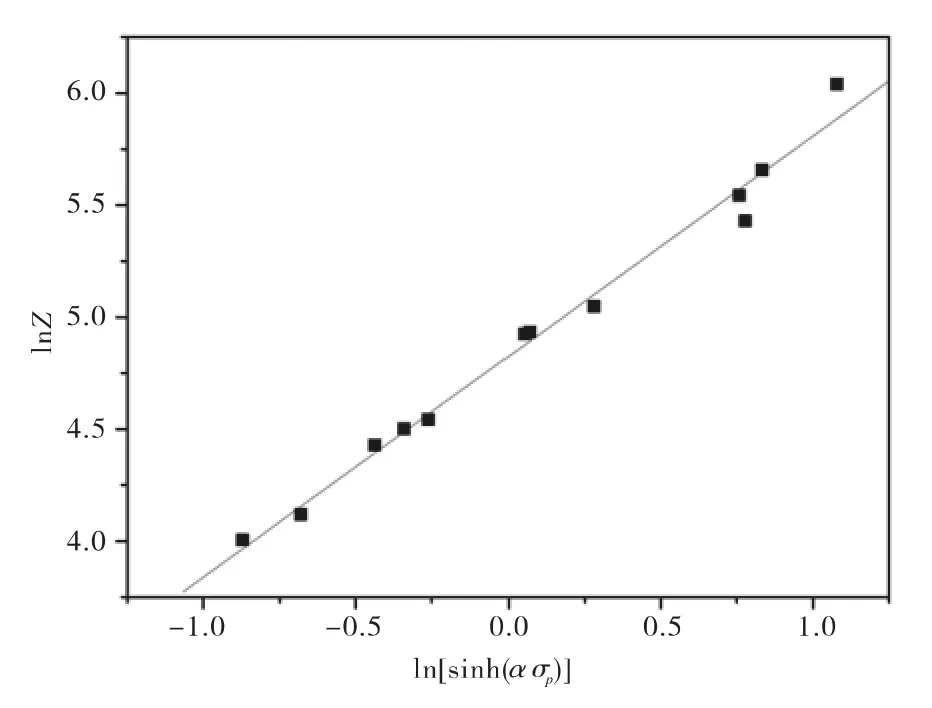
图7 lnZ 与 ln[sinh(ασp)]关系图Fig.7 Relationship between ln[sinh(ασp)]and lnZ

由图7可以看出lnZ与ln[sinh(ασp)]呈线性关系，其线性相关度达到99.3%，由此表明可以用双曲正弦函数来描述高温热变形过程的本构关系。而lnA为线性回归的截距，则lnA=29.053 3，则A=4.15×1012S-1;将拟合出的各个数据带入双曲正弦函数，可得到本构方程:

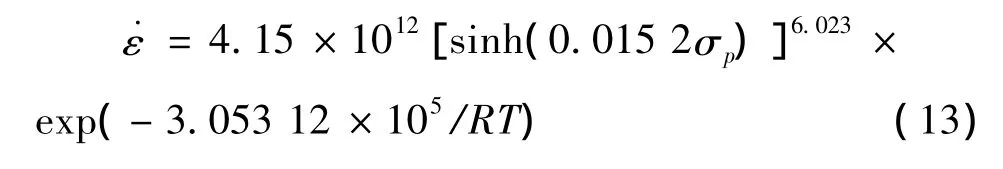
则Z参数可表示为:

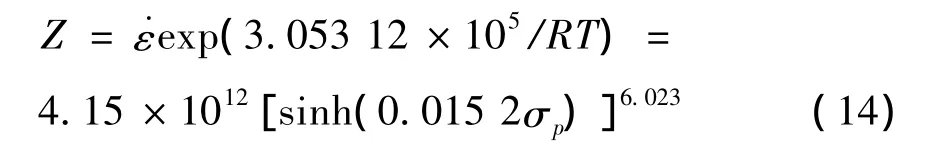
3 结论

(1)通过对铸态钢2.25Cr1Mo0.25V高温形变过程中应力-应变曲线的研究得出，随着形变温度的升高和应变速率的减小，流变应力减小，峰值应力和应变降低，但应变速率为0.005 S-1和0.01 S-1时，4个温度下的流变应力值较为接近。

(2)确定高温变形过程中的形变激活能Q为305.312 kJ/mol，并建立该过程中的本构方程为:

˙ε=4.15×1012[sinh(0.015 2σp)]6.023×exp(-3.053 12 × 105/RT)

[1]陈晓玲，李多民，段滋华.加氢反应器的发展现状[J].化工装备技术，2009，30(1):29-30.

[2]张景利，付瑞东，王纯宇，等.2.25Cr-1Mo-0.25V 钢的热变形行为及其形变组织[J].塑性工程学报，2010，17(3):45-49.

[3]RAO K P，H AW BOLT E.Development of constitutive relationships using compression testing of a medium carbon steel[J].Transactions of the ASME Journal of Engineering Materials and Technology，1992，114(1):116-123.

[4]HEE Y.KIM ，SOON H Hong.High temperature deformation behavior and microstructral evolntion of Ti-47Al-2Cr-4Nb intermetallic alloys[J].Scripta Materialia，1998，38(10):1517-1523.

[5]GRONOSTAJSKI Z J.Development of constitutive equation of copper-silicon alloys[J].Journal of Materials Processing Technology，1996，60(5):621-627.

[6]柏永清，陈明明，陈慧琴.316LN热变形行为及动态再结晶晶粒的演变规律[J].太原科技大学学报，2009，30(5):424-425.

[7]ZENER C，HOLLOMON J H.Effect of strain-rate up on the plastic flow of steel[J].J Appl Phys，1944，15(1):22-32.