起重机起升机构串电阻启动时刚性动载荷分析

冯 亮，文 豪，王全伟，张 君，陈言亭

(太原科技大学机械工程学院，太原030024)

起动机传动机构在启动和制动等工况突变时，产生的刚性动载是不可忽视的。GB/T3811《起重机设计规范》给出了计算管行动载系数的简单计算方法。但并未将影响该系数的电动机启动方式，机构间隙考虑在内。

Tt—— 启动转矩(N·m);

Tr—— 静转阻矩(N·m);

J1——靠电动机侧的惯量(kg·m2);

J2——靠低速轴侧的惯量之和。

为了便于计算，起重机通常用动力系数值来表示载荷的大小动力系数的定义是最大振动载荷与静载荷的比值，对于传动零件则是最大振动载荷力矩与电动机额定力矩之比。

1 建立系统模型[1]

1.1 电动机启动力矩

绕线式异步电机一般都是用串入转子电阻的方法启动，其启动过程见图1(a)为减少冲击载荷，在绕线电机的启动电阻中增加一个预备档电阻，(即图1中的特性曲线0)，机构启动时附加接入这个预备档电阻，电动机便产生约等于电动机额定力矩的75%的力矩，以消除传动机构中的间隙，并产生一定的预紧力，但尚不至于使机构启动，这样可以显著地减小振动载荷。

图1 绕线电动机串电阻启动Fig.1 The serial-resistance startup of wire-wound motor

从图1(a)[2]中可看出，绕线式电机的启动过程是:机构启动时先附加一个预备档电阻具有最大启动力矩Mmax，然后力矩随速度升高而减小，逐段切去电阻，力矩按图图示阶梯级曲线变化，直至全部切去电阻，按电动机自然特性曲线运转。但是经过分析，电动机在切去第一档电阻时速度从零启动，以后每切换一档电阻其产生的动载都小于第一档的振动载荷。所以在求机构的最大振动载荷时，

式 中: ωs—— 电 动 机 同 步 转 速 (角 速度，rad/s);

Tt0——电动机启动转矩(N·m)

1.2 起重机起升传动系的数学建模

起重机机构的振动载荷计算，以两质量单自由度系统最为合适。一般认为系统自由度越多，计算结果越精确，其实不然，以金属结构为例，如果在起重机金属结构有限元分析中，将起升质量作为质量矩阵中的一个元素，那么这个矩阵一定是奇异的，用这样的矩阵参与计算，一定会造成发散的计算结果。刚度矩阵也有类似的情况出现，所以在起重机有限元分析中，要对这些情况作特殊处理。[3]

在传动系统中，转动惯量相当于平移系统中的质量m.在比较转动惯量大小时，一般要把它们转换到同一传动轴上才有意义。一般是把他们换算到电动机轴上。经过换算，齿轮的J与电动机转子和联轴器的惯量相比就是很小的量。在实际计算中以计算轴为基点，将转动惯量分为两部分:靠电动机侧的惯量之和记为J1;靠低速轴侧的惯量之和为另一侧，记为J2;然后将J1和J2之间用无质量的弹性轴联系起来，弹性轴的弹性系数为k，这样就构成了两转动惯量的力学模型[4]，其中J1的广义坐标为θ1，J2的广义坐标为θ2，对这两个转动惯量分别应用牛顿第二定律，可得如下两个运动方程[5]:首先求得第一档就可以。

将上述的电机启动特性，用数学表达式表示为:

令:θ=θ1-θ2将式代入式(2)加以整理，以相对坐标θ表示，可得单个的运动方程:

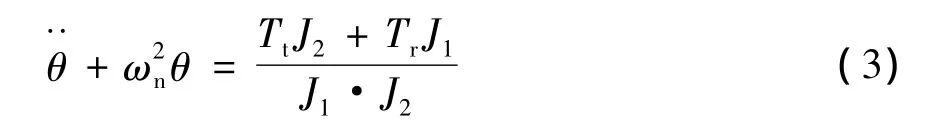
式中ωn为系统的固有频率，由式(4)计算得:

式(3)的全解为:

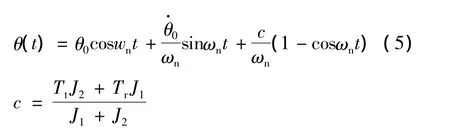
由于制造的原因，不可避免的会产生误差，传动机构总是存在一定的间隙。机构存在间隙，启动和制动是存在冲击，造成较大的动载荷。机构的间隙启动过程可以分为三个阶段，第一阶段:电动机启动，传动系统空转以消除间隙;第二阶段:传动机构开始接触并产生弹性变形，直至弹性转矩等于外阻转矩;第三阶段:整个系统成为一体继续振动。

第一阶段:电动机加速J1直至间隙消除，这时J1已具有初速度ω0但J2尚未运动。

第二阶段:J1与J2开始接触并产生弹性力，当弹性力增加到能够克服静阻力Tr时，这一阶段结束，这时轴的角速度:

第三阶段:从J2参与运动开始，整个系统产生振动。这一阶段的初位移是:θ1=Tr/k，初速度为式(6)表示的ω1.设为阶跃激励c，应用式(5)可得轴的转矩表达式:

于是得到最大值:

将有关常数代入，经整理得到最大转矩表达式为:

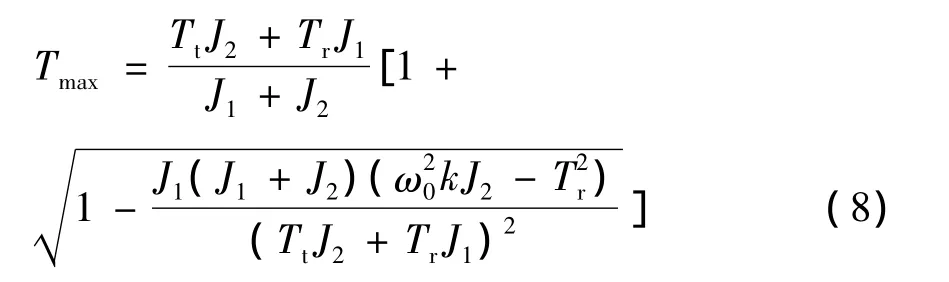
机构有间隙时的计算公式为式(8)为了观察传动间隙对动载荷的影响，这节做进一步分析。由于齿轮本身的转动惯量相对来说非常小，可以忽略不计，因此齿轮传动中各级间隙可以累计到高速级进行处理，其总间隙量以θ0(弧度)表示。

在式(8)中，间隙的影响通过ω0来表示，ω0是电动机驱动转动惯量J1直至间隙消除那个瞬间J1所具有的角速度。设这一阶段是等加速度运动，角加速度为:ε0=Tt0/J1

若这一阶段加速所需时间为t0，则根据运动学有:

从此得:

将式(10)代入式(8)，并应用α，β，ξ等无因次量取代，若用 Tmax表示产生的最大转矩，φ =，则:

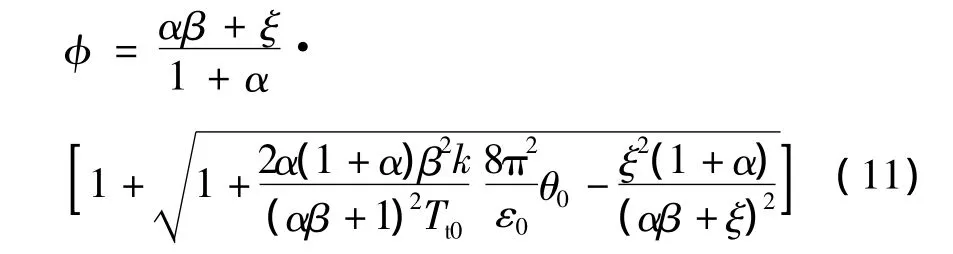
根据刚性动载洗系数的定义:

式中，φ5—— 弹性系数，φ5=2- ξ/β.

2 对有间隙起升机构的关系动载系数的分析

因为k/Tt0表示传动机构扭转刚度的相对值，它的倒数可表示为:

θn=Tn/k为传动机构在电动机额定转矩作用下的静扭转角，式(12)可进一步化简。于是从上述建模可得 φ 为 α，β，ξ，θ0等参数的函数。即:φ =f(α，β，ξ，θ0)

为了确定上述各因数对刚性动载系数的影响，必须先确定其他三个变量，才能得出所研究的变量与刚性动载的关系[6]。

一般情况下起升机构中α=1，运行机构和回转机构中α≥5启动转矩倍数β平均的取为1.6，ξ=0.5，θ0=1°～ 10°[3].下面通过固定其他变量，重点分析一个变量的方法，分析个变量与惯性动载荷的关系。本文推导公式为式(12)，原使用公式为:

下面对各个参数利用工具Matlab进行分析[7]。

(1)研究α与β的关系

表1 α与φ的关系Tab.1 The relationship between α and φ

图2 α与φ的关系Fig.2 The relationship between α and φ

由此可见本文推导出的公式与原不考虑间隙时的公式算出的刚性动载系数偏大，但α大于5以后所得的刚性动载增长率放缓。但是两公式的趋势是基本一致的。当α≥8时，ξ对φ的影响很小。在运行机构和回转机构中，α值均较大，故可略去静阻力[8]，即令 ξ=Tr/Tn=0，式(11)可简化为:

(2)分析β与φ的关系

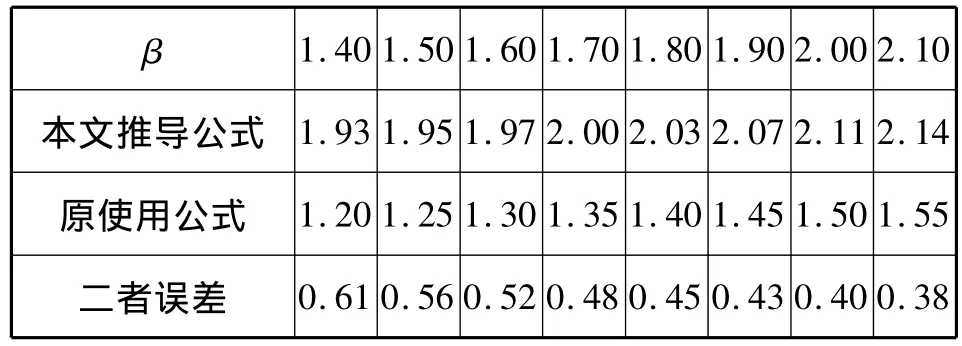
表2 β与φ的关系Tab.2 The relationship between β and φ

启动转矩倍数与刚性动载系数呈线性关系，两公式算出的平均误差为一倍。总体趋势是非常相似的。同时说明，启动转矩越猛烈，惯性动载越大，对机构的作用越不利。通常在启动前预加一个适当的预紧力。

图3 β与φ的关系Fig.3 The relationship between β and φ

(3)分析θ0与φ的关系

由表3和图4可以清楚的看出间隙对刚性动载系数影响很大，由于原公式没有考虑到间隙的作用，所以是一条水平直线，与间隙无关。

3 结论

利用二质量单自由度的起升机构模型，分析了刚性动载系数。将《起重机设计规范》(GB3811-83)未能考虑进去的一些影响因素考虑在内，使得模型的精度有一定提高。分析后得出的结论与预期的实际情况相似，这说明本文推导出的公式符合实际情况。能更加精确地描述起重机起升机构的刚性动载荷。

由上述的图表以及公式可得出如下几点:

(1)在其他条件相同时，间隙θ0越大，动载系数也越大。

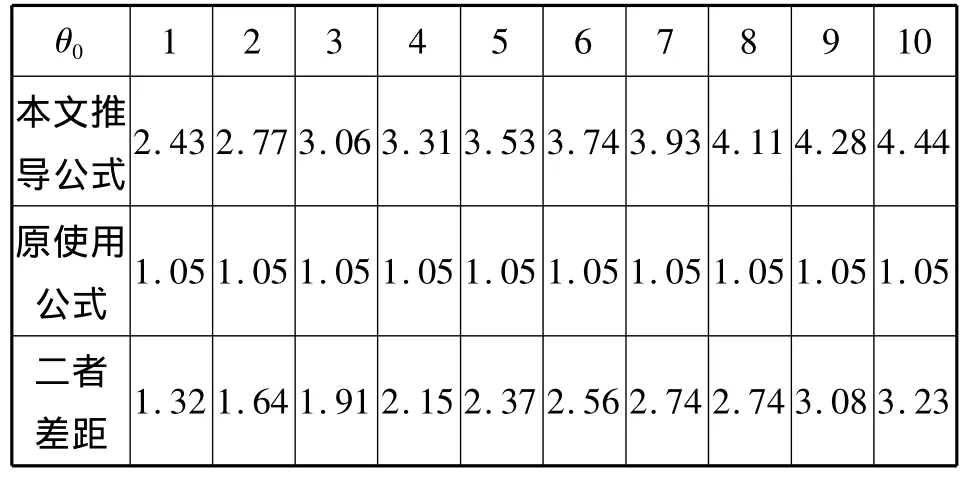
表3 θ0与φ的关系Tab.3 The relationship between θ0and φ

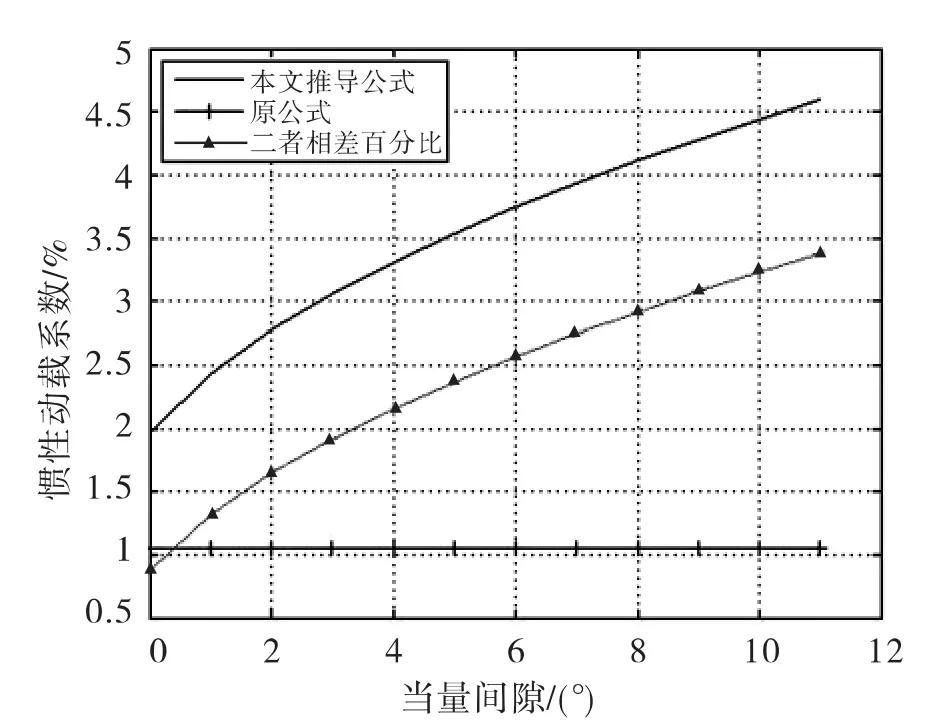
图4 θ0与φ的关系Fig.4 The relationship between θ0and φ

(2)其他条件相同时，系统的自振周期越大，刚性动载系数越小。

(3)在间隙值相同时，电动机驱动力矩不变时J1越小，刚性动载系数越小。

(4)当α值增大时，刚性动载系数也增大，但当α≥5时，刚性动载趋于定值。

[1]胡宗武.起重机设计与实例[M].上海:机械工业出版社，2008.

[2]李发海，王岩.电机拖动与基础[M].北京:清华大学出版社，2005.

[3]HAO WEN，QUANWEI WANG，GUANG ZHENG，et al.Analysis on the Super-winding Accident of Casting Crane and Contiguration of the Safeguard[J].Advances Materials Research，2011，145(11):390-393.

[4]胡宗武.起重机动载荷的简化计算[J].起重运输机械，1982(2):2-9.

[5]刘少武，张继福，高崇仁.起重机械检验挖掘系统的设计与实现[J].太原科技大学学报，2011，32(5):398-402.

[6]李宏娟，陶元芳.桥门机主梁设计时强度与刚度的关系[J].太原科技大学学报，2011，32(1):28-32.

[7]范元勋，卜廷春，李水水，等.基于ADAMS/MATLAB的桥式起重机起升动载荷的联合仿真[J].重型机械，2005(5):30-32.

[8]陶元芳，谢文宁，沈才华.起重机起升机构可视化CAD软件的应用.西安[J].重型机械，2007(4):15-25.