非均匀桨结合后掠桨尖的旋翼厚度噪声研究

李东红，黄庆彩，杨亦春

(1.太原科技大学电子信息工程学院，太原030024；2.中国科学院声学研究所，北京100190)

直升机的噪声问题严重制约了直升机在实际中的应用。探索降低直升机噪声的方法是直升机研究和发展的重要课题之一。Farassat给出了亚音速下旋翼噪声的计算公式[1-2]，徐国华利用Farassat提出的方法计算了直升机的噪声[3]。Farassat还分析了桨尖后掠对噪声的影响，发现后掠可以降低桨叶产生的噪声[4]。王立群、宋文萍等人利用Kirchhoff方法分析了桨尖后掠对高速脉冲噪声(HSI)的影响[5-6]，结果表明桨尖后掠可以降低噪声峰值。孙晓峰等介绍了一种针对后掠叶栅噪声的远场分析方法[7]。P.A.Shahady分析并试验验证了桨叶间距非均匀对噪声的影响，发现非均匀桨可以减低噪声线谱的幅值[8]。Brentner、蔡伟等人分析了桨叶间距非均匀对旋翼噪声的影响[9-10]。Bryan Edward等将非均匀桨作为旋翼噪声控制的重要手段之一[11]。W.Dobrzynski研究了将桨叶间距非均匀用于螺旋桨时的噪声变化并开展了相关的试验[12]。

采用后掠桨可以降低旋翼的噪声，而非均匀桨可以改变噪声的频谱特征，因此本文主要分析二者结合后对厚度噪声的影响，包括对比厚度噪声的声压级和指向性两方面的变化以及不同调制模式及后掠角度对噪声的影响，从而为旋翼噪声的分析和控制提供有益的借鉴和指导。

1 厚度噪声的计算方法

旋翼噪声通常可分为厚度噪声、载荷噪声和四极子噪声。厚度噪声是指直升机旋翼在运动过程中由于排开空气引起压力扰动而产生的噪声，主要与桨叶的几何形状和飞行状态密切相关。厚度噪声属于单极子噪声，其传播方向主要在桨盘平面内。Farassat对 FW-H方程进行了求解，得到了Formulation 1A 解[1-2]。根据 Formulation1A 公式，在亚音速条件下若忽略四极子噪声，旋翼噪声则表示为厚度噪声和载荷噪声之和，其中厚度噪声的预估计算公式如下[1-2]:

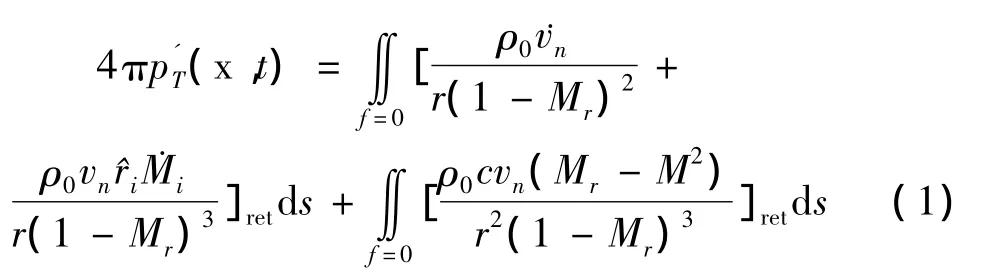
相关的理论分析及具体计算过程可参见Brentner等人的研究结果[13]。在前飞条件下，厚度噪声是桨盘平面的主要噪声成分，其数值远大于载荷噪声的计算结果[13]，因此本文主要针对厚度噪声来展开研究。在计算前飞条件下的桨叶噪声时，通常分析随直升机一起移动的观测点的噪声。若设直升机的速度为V(t)，则任意t时刻移动坐标系的原点在大地坐标系的对应向量X0(t)表示为[2]:

若计算移动坐标系内点X的声压则等同于计算大地坐标系内点X+X0(t)的声压，即:

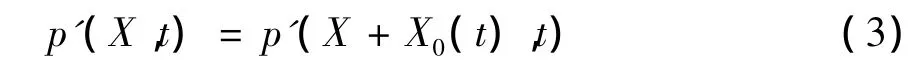
此外，关于噪声计算时的延时方程的求解方法以及如何分析桨叶刚性振动等参数的影响可参见相关的文献[13]。为了说明噪声计算方法的有效性，本文计算了文献14中的算例。其中观测点在桨盘平面内距离桨毂中心约4 m处的声压，具体位置为(3.27，-2.16，-0.17)，如图1 所示。其中桨叶的半径为 1.829 m，弦长为 0.133 4 m，翼型为 NACA0012，共2片桨叶。旋翼转速为1 300 rpm，前飞速度为 41.4 m/s.声速 c0为 350.1 m/s，桨盘倾斜角 αt为 -8.76°[14-15]，计算结果如图 2 所示。

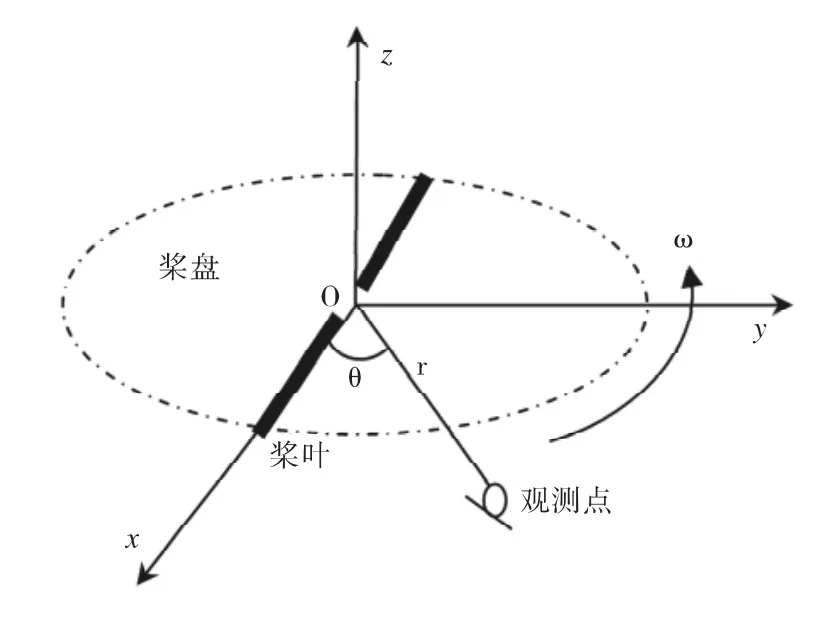
图1 厚度噪声观测点位置示意图Fig.1 Schematic of observer positions of thickness noise

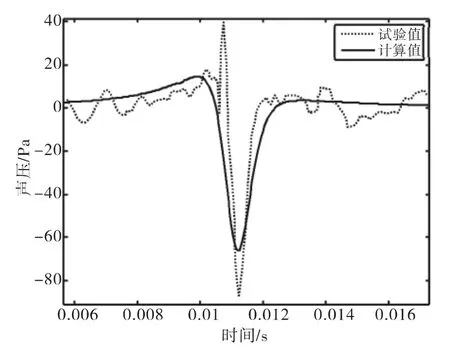
图2 本文计算结果与试验数据的对比Fig.2 Comparison of numerical results and the experimental results

从图2中可见，本文所计算的厚度噪声基本上反映了旋翼在桨盘平面的噪声变化规律。

2 桨尖后掠对厚度噪声的影响

桨尖的改型是提高旋翼性能的一个重要途径。后掠桨尖除了可提升悬停效率外，在削弱激波方面也有明显的作用[16]。后掠桨尖带来气动性能改善的同时，也会相应降低旋翼产生的噪声。本文所分析的后掠桨尖的结构如图3所示。

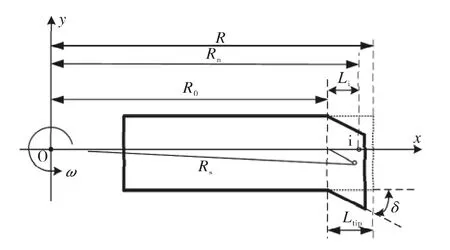
图3 后掠桨叶结构示意图Fig.3 Schematic of configuration of the blade with swept tip

图3中O为转轴中心，旋转角速度记为ω，无后掠时的桨尖长度 Ltip=0.05*R.其中xoy所在平面对应桨叶的旋转平面，桨尖后掠的起始位置记为R0，桨尖处无后掠时某一点的坐标为(x0，y0，z0)，则桨尖后掠后该点的坐标(xs，ys，zs)应满足下式

为了问题的简化，仅分析1片桨叶。观测点位于桨盘平面内距离桨毂中心3 m处。后掠角δ的变化范围为0～80°，其中后掠角为0°的情况相当于无后掠。不同后掠角的厚度噪声计算结果如图4所示，相应的转速为1 296 rpm，桨叶的弦长为0.133 4 m，翼型为n12，桨叶半径R为1.829 m.

从图4中各条曲线的对比可见，采用后掠桨尖可以明显降低厚度噪声，而且随着后掠角的增大，负向脉冲峰值减小。厚度噪声声压级随后掠角的变化如图5所示。

从图5中可见，随着后掠角的增大，使桨叶产生的厚度噪声明显降低。桨尖后掠80°时的厚度噪声声压值比无后掠时的声压值减小约3 dB.

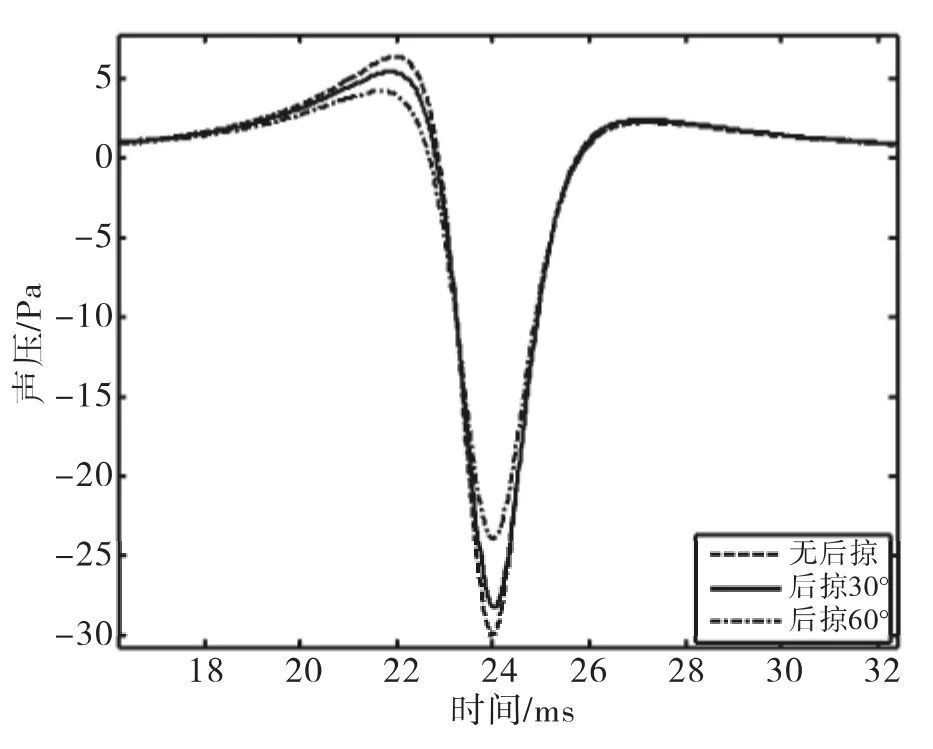
图4 悬停状态下不同后掠角的厚度噪声对比Fig.4 Comparision of thickness noise of hovering rotor with various swept angles

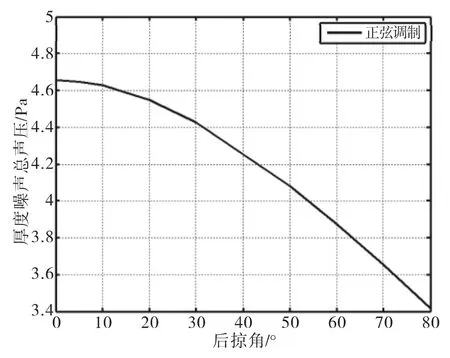
图5 声压有效值随后掠角的变化曲线Fig.5 Overall sound pressure of thickness noise via swept angle

3 非均匀桨叶间距与桨尖后掠对厚度噪声的影响

3.1 悬停状态下的声压级

非均匀桨是指桨叶间距不均匀，假设均匀间距情况下某一个桨叶的相角为θi，经过正弦调制后的桨叶相角为 θ'i，则:

其中i=1，2，…N;N为桨叶的总数。调制参数b表示桨叶间夹角变化量的最大值，m表示调制的循环次数。θi为桨叶间距均匀条件下第i片桨叶相对于桨叶起始位置θ0=0之间的夹角。

非均匀桨可以改变噪声的谱线特征，主要是降低桨叶通过频率的谱线峰值，而桨尖后掠可降低噪声。如果将二者结合，则可以发挥其各自的优点，即在获得一定降噪效果的同时减弱噪声的特征。因此本文对桨叶周向间距非均匀桨且桨尖后掠的5桨叶旋翼厚度噪声进行了数值计算，相关参数同前文所述，悬停状态下桨盘平面内距离桨毂中心3 m处的计算结果如图6所示。

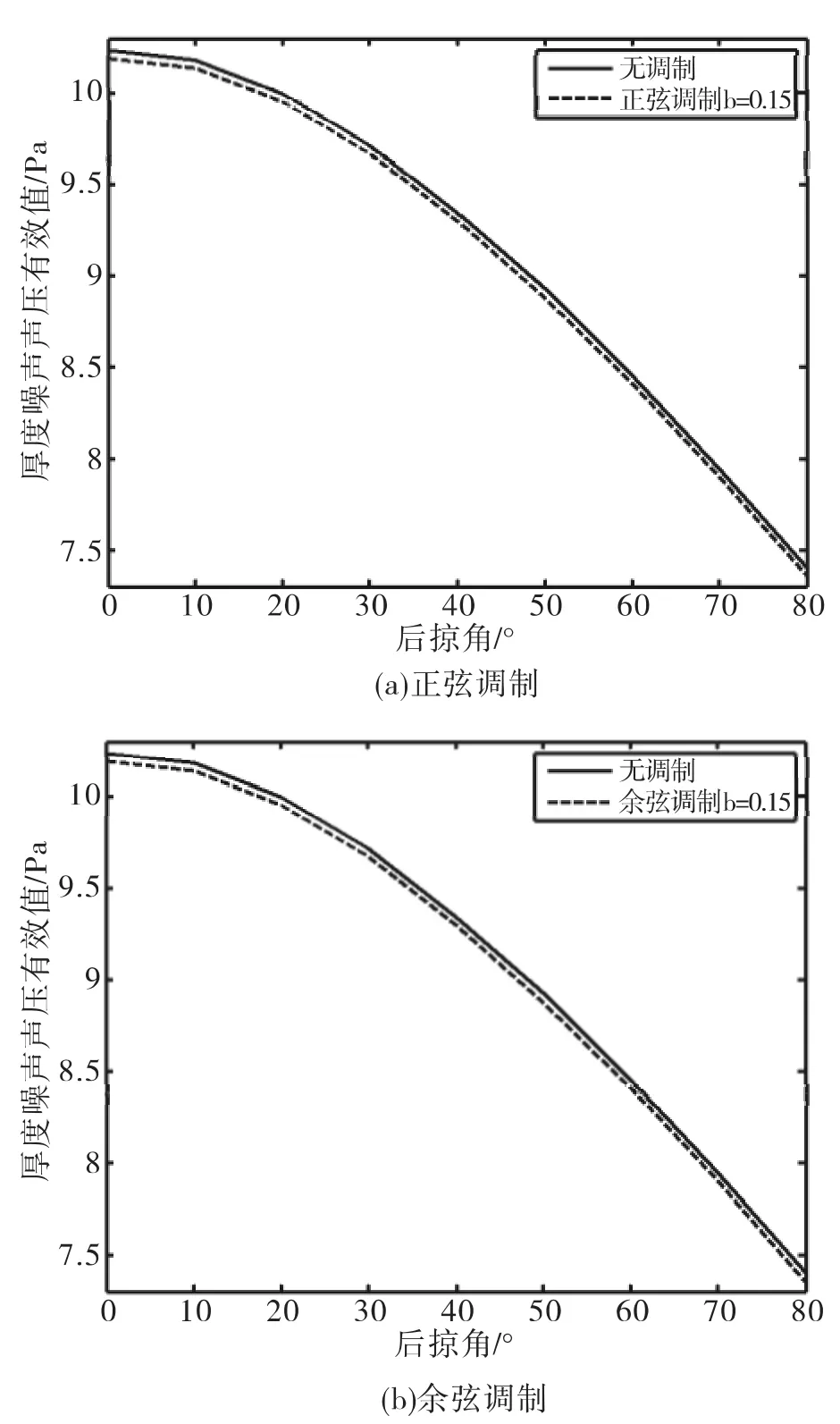
图6 非均匀+后掠桨厚度声压有效值随后掠角的变化曲线Fig.6 Overall sound pressure of thickness noise for rotor with uneven blade spacing and swept tip via swept tip angle

通过比较图6中两种调制方式在相同条件下的声压有效值，可见随着后掠角度的增大，厚度噪声声压的有效值都随之降低。结合桨叶间距调制和桨尖后掠的方式比相同条件下只采用后掠的方式进一步降低厚度噪声。对比均匀桨和采用正弦调制(b=0.15)非均匀桨的噪声频谱可见，将桨叶间距非均匀调制与桨尖后掠二者结合可以使厚度噪声主要线谱的幅值明显降低，但是桨叶通过频率及其谐频外的其它频率上的线谱幅值有可能增大。

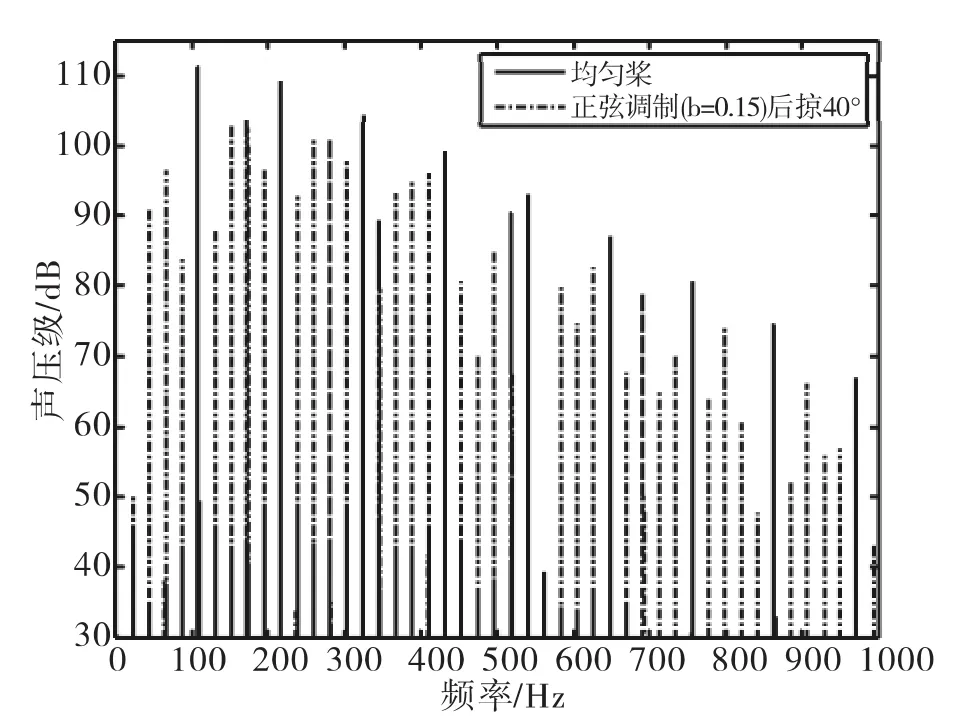
图7 正弦调制参数b=0.15且后掠角δ=40°时非均匀桨与均匀桨的频谱对比Fig.7 Comparison of spectra of thickness noise between normal rotor and rotor with uneven blade spacing(b=0.15，δ =40°)

3.2 后掠非均匀桨的指向性

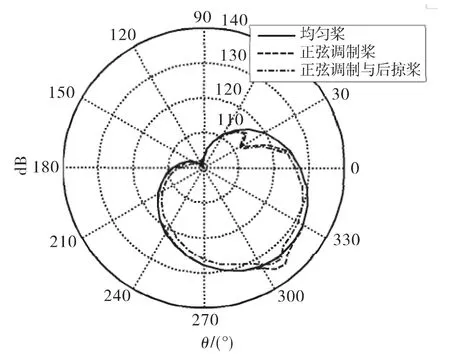
图8 桨盘平面内厚度噪声指向性Fig.8 Directivity pattern of thickness noise in rotor disc plane

本文计算了前飞速度为60 m/s时位于桨盘平面内距离桨毂中心3 m处的均匀桨和桨尖后掠40°的非均匀桨(正弦调制参数b=0.15)厚度噪声的指向性，如图8所示。从图8可知，由于前飞速度的影响，桨盘平面内厚度噪声的指向性图具有一定的特点，即出现了噪声声压级的峰值和谷点。此外，桨叶间距均匀桨和非均匀桨的厚度噪声指向性具有明显的区别。由于桨叶间距的调制作用，桨盘平面内的厚度噪声指向性相比于均匀桨的情况发生了一定的改变。桨叶间距调制后，可以降低某一方向上的噪声声压级(图8中θ=30°方向)，但是会导致另一方向上噪声的增强(图8中θ=310°方向)。如果在调制桨叶间距的同时，考虑桨叶桨尖的后掠，则可以使旋翼的噪声相比于无后掠的情况降低，且指向性曲线的变化趋势同非均匀正弦调制桨大致相同。

4 结果分析

无后掠时，假设桨尖处的某一点为i，其距离转轴的中心为R0+Li，显然，由于旋转，该点相应的线速度为ω(R0+Li)。在桨尖后掠角为θ时，同一点的线速度变为ωRs，如图3所示。由于R0+Li＞Rs，因此桨尖后掠的线速度小于无后掠的情况，而从厚度噪声的计算结果来看，桨尖处的噪声与速度密切相关，桨尖处的速度越大，产生的噪声也越大。因此通过桨尖后掠可以降低桨尖处的速度，进而降低其厚度噪声。

前飞时，对于前行桨叶由于其速度等于线速度与前飞速度之和，因此其附近的噪声得到了明显的增强。对于后行桨叶，其速度等于线速度与前飞速度的差，故其附近的噪声相对减弱。前行和后行桨叶的速度差异造成了声场的分布差异。

桨叶间距的非均匀主要是改变了厚度噪声的频谱特征。引起的主要变化是使噪声的频谱从均匀桨情况下的一个桨叶通过频率和其谐频变为多个桨叶通过频率。将非均匀桨和后掠桨尖二者相结合，可在降噪的同时使频谱特征也得到改变。

5 结论

非均匀桨可以降低旋翼厚度噪声的频谱特征，而采用后掠桨尖则可以降低旋翼噪声，将二者结合可在获得降噪效果的同时减弱噪声的频谱特征，这对于提高直升机的反探测能力具有十分重要的意义。使用该方法时必须考虑到桨叶间距调制对流场的影响，如对载荷平衡的影响，因此可酌情选择调制系数和后掠角。

[1]FARASSAT F.Theory of noise generation from moving bodies with an application to helicopter rotors[R].NASA Technical Report，TR R-451，1975.

[2]FARASSAT F.Derivation of Formulations 1 and 1A of Farassat[R].NASA Technical Memorandum，TM-2007-214853，2007.

[3]徐国华，高正.直升机旋翼旋转噪声的估算[J].南京航空学院学报.1991，23(2):20-26.

[4]FARASSAT F.Bounds on thickness and loading noise of rotating blades and the favorable effect of blade sweep on noise reduction[R].NASA Technical Report，1978.

[5]王立群，宋文萍.旋翼桨尖形状对噪声影响量级的研究[J].航空学报.2000，21(1):48-51.

[6]宋文萍，韩忠华，王立群等.旋翼桨尖几何形状对旋翼气动噪声影响的定量计算分析[J].计算物理.2001，18(6):569-572.

[7]孙晓峰，周盛.气动声学[M].北京:国防工业出版社，1994.

[8]SHAHADY P A，LYON C A，SCHAUER J J，et al.The Effect of Modulated Blade Spacing on Static Rotor Acoustics and Performance[J].AIAA，1973，44852.

[9]BRENTNER K S，EDWARDS B D，RILEY R，et al.Predicted noise for a main rotor with modulated blade spacing[J].Journal of the American Helicopter Society，2005，50(1):18-25.

[10]蔡伟，王阳，招启军.应用非均匀桨叶设计方法的旋翼降噪技术研究[J].直升机技术，2008，3:86-91.

[11]EDWARDS B，COX C.Revolutionary concepts for helicopter noise reduction-S.I.L.E.N.T program[R].NASA Contractor Report，CR-2002-211650，2002.

[12]DOBRZYNSKI W.Propeller noise reduction by means of unsymmetrical blade-spacing[J].Journal of Sound and Vibration，1993，163(1):123-136.

[13]BRENTNER K S.Prediction of Helicopter Rotor Discrete Frequency Noise:A Computer Program Incorporating Realistic Blade Motions and Advanced Acoustic Formulation[R].NASA Technical Memorandum，87721，1986.

[14]CONNER D A，HOAD D R.Reduction of high-speed impulsive noise by blade planform modification of a model helicopter rotor[R].NASA Technical Memorandum，84553，1982.

[15]BRENTNER K S.Prediction of helicopter rotor discrete frequency noise for three scale models[J].Journal of Aircraft，1987，25(5):420-427.

[16]徐广，招启军，王博，等.先进直升机旋翼悬停状态气动性能计算[J].航空学报，2010，31(9):1723-1732.