基于TEQ的固定边界托卡马克等离子体平衡模拟

刘志远， 李国强， 徐立清

（中国科学院 等离子体物理研究所，安徽 合肥 230031）

基于TEQ的固定边界托卡马克等离子体平衡模拟

刘志远， 李国强， 徐立清

（中国科学院 等离子体物理研究所，安徽 合肥 230031）

文章设计了新的TEQ计算流程，实现了由磁面位置及磁面上磁通值计算网格点上磁通的算法，修正了TEQ求解固定边界托卡马克等离子体平衡时输出g－file的程序，并以EAST装置为基础，用剪切和反剪切2种情况的安全因子、压强分布进行了检验，发现TEQ的结果与EFIT符合得很好，最后用TEQ构建了6组反剪切固定边界平衡，简单分析了压强对磁轴水平位置的影响。

TEQ程序；g－file程序；EAST装置；固定边界等离子体平衡；数值模拟

0 引 言

NTCC（National Transport Code Collaboration）［1］中的 TEQ 程 序 是 一个通过 数 值 求 解Grad－Shafranov方程来计算托卡马克磁流体力学平衡的程序，它是从Corsica［2］中独立出的，可以求解自由边界平衡，也可以求解固定边界平衡，是一个很强大的程序库［3－4］。

在托卡马克研究领域，最常用的平衡数据文件格式是 EFIT 程序［5］输出的 g－file，g－file几乎已经成为行业标准。但NTCC中的TEQ程序不能读取g－file，因此，本文对TEQ这方面的功能进行了补充并重新设计了相应的程序模块，对读入g－file的程序重新编写，修正输出g－file的程序中的不足，实现了由磁面位置及磁面上磁通值计算网格点上磁通的算法，并设计了新的程序流程，调整了部分参数。通过数据验证，发现TEQ所得的计算结果与EFIT计算所得的结果吻合得比较好。用TEQ可以构建多种平衡，计算所得的数据可以用来分析压强对磁轴位置的影响，还可以进一步分析平衡的稳定性，也可以为构建新的平衡提供一种依据并为设计新的装置提供一种参考。本文所有的计算都是以EAST（Experimental Advanced Superconducting Tokamak）装置为基础进行的。

1 托卡马克等离子体平衡方程

由单流体MHD方程描述的等离子体平衡由（1）式表示，即

其中，p为等离子体压强；B为磁感应强度；j为电流密度。在轴对称情况下，由（1）式可以得出角向磁通ψ所满足的Grad－Shafranov方程：

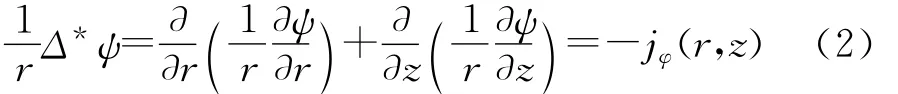
其中，（r，φ，z）表示柱坐标；jφ（r，z）为大环方向电流密度。

方程（1）所表示的平衡中，磁面就是ψ＝const表示的面，磁面也是平衡位形的等压面，且j只有在磁面上的分量［6］，由此可得：

其中，Ψ和F分别为相对于对称轴r＝0的角向磁通和电流通量。

轴对称等离子体的MHD平衡由准线性椭圆方程（2）和方程（3）来决定。一般情况下，给定P（ψ）和f（ψ）的具体函数形式，加上合适的边界条件，就可以解出ψ＝ψ（R，Z），已知ψ后，就可以给出平衡位形的所有物理量［7］。

在给定P（ψ）和q（ψ）求解平衡问题时，考虑角向磁通的守恒条件为：

其中，ψm为磁轴处的角向磁通；ψb为边界处的角向磁通。

在磁面上安全因子的分布为：

其中，Φ为穿过ψ＝const截面的环向磁通。

由f（ψ）和q（ψ）的定义，可得积分区域为ψ＝const所形成的环面，即

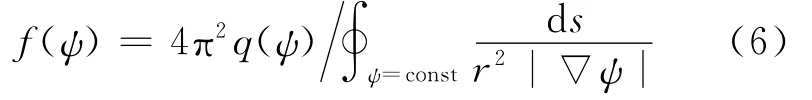
由（2）式、（3）式、（6）式可见，对于所考虑的平衡问题，只要知道P（ψ）和q（ψ）就可以了。引入对相邻磁面间体积V（ψ）的平均：

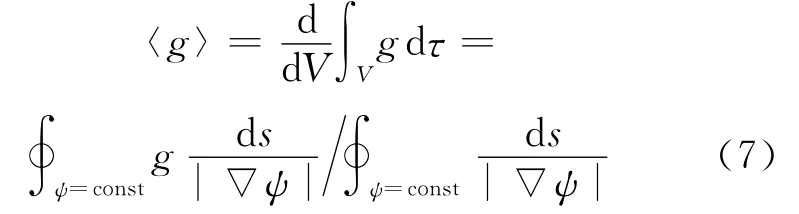
可以得到：

将（2）式写为非线性积分微分方程的形式，即

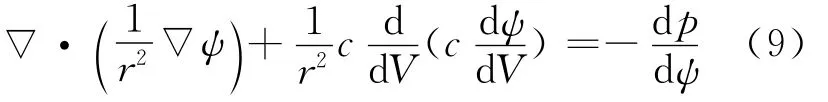
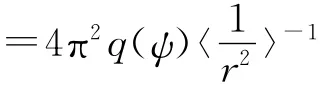
对（9）式取平均后，可得：

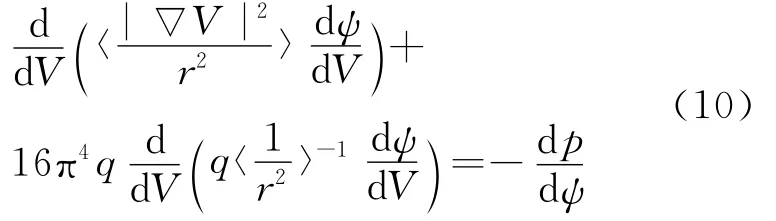
在给定了（4）式中的后，就可以得到方程（9）的唯一解［8］。

在程序中，一般用表示归一化的ψ，即

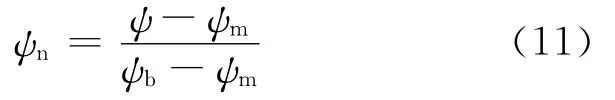
其中，ψm表示磁轴处的角向磁通；ψb表示边界处的角向磁通。为方便表示，后面也将ψn简记为ψ。另外，也用（12）式表示（3）式中的f［9］，即

2 TEQ读取g－file并进行计算

TEQ本身可以使用自由边界和固定边界2种方法求解等离子体平衡方程，但是由于这2种方法的计算原理不同，它们使用的变量也不相同。本文首先使用自由边界开始计算，需要注意的是，使用自由边界只是使TEQ程序开始运行的一种手段。用自由边界设定计算区域后，将自由边界转变为固定边界，再逐个改变需要改变的物理量，包括边界的位置、安全因子分布、压强分布以及控制程序运行的参数等，输出数据后再与EFIT所得结果进行对比。基本的流程如图1所示。

在使用固定边界求解Grad－Shafranov方程时，选取常用的q和P的位形作为计算平衡的输入数据，这些数据都从由EFIT计算出的g－file中获得。g－file中包含许多信息，但并不全部需要，一般只需要知道计算区域、固定边界位置、真空时磁轴处的磁感应强度、真空时磁轴的横坐标、等离子体电流、安全因子分布和压强分布即可。

图1 新的TEQ程序处理流程

通过EFIT－viewer可以得到平行方向电流的分布，它是衡量TEQ计算结果好坏的重要标准。此外，还需要对比磁面的分布，由于EFIT求解得到的是网格点上的磁通值，进而可以得到其等值线，而TEQ使用固定边界求解得到的是磁面的位置，因此在对比的时候只要两者不出现相交的情况，即认为计算是合理的。

在计算的过程中，需要注意的是TEQ使用的单位与EFIT使用的单位是不相同的，需要对g－file中的数据进行相应处理后才能进行计算。

3 TEQ 输出g－file

TEQ本身也可以产生g－file，但直接利用TEQ自带的程序输出的结果并不理想，输出的F、磁面位形与EFIT的计算结果有差别。

经过检查程序，发现TEQ默认以计算区域的中心的横坐标为真空时磁轴的横坐标，而一般情况下，这两者可能并不相等。

例如采用的EFIT的计算区域，即左边界为120cm，右边界为260cm，则TEQ默认的磁轴位置在190cm处，而实际上真空时磁轴位置（EAST）在185.8cm 处。根据（12）式对F进行修正后发现，它可以与EFIT的计算结果符合较好，因此需要在程序中人为地指定真空时磁轴的横坐标，然后再进行计算。

对于磁面位形的差别，经过对TEQ程序的分析，发现这主要是由于自由边界和固定边界的计算方法不同引起的。

自由边界计算时，会对整个计算区域进行计算，当把自由边界转化为固定边界时，程序会根据自由边界的计算结果来确定一组磁面的位置，而之后再以固定边界计算时，程序都不会再计算最外闭合磁面以外的区域，即TEQ自带的输出g－file的程序输出的其实是最后一次自由边界计算时的磁面位形。固定边界是对磁面位置进行计算，而自由边界是对网格点上的磁通进行计算。

因此，固定边界的计算结果没有办法以网格的形式直接输出。但用固定边界可以直接输出磁面的位置以及磁面上的磁通值，这相当于一组等值线，而输出g－file需要的则是这样一种网格，利用网格上的点可以画出与固定边界所给出的磁面相同的磁面位形，因此，设计了用磁面位置及磁面上磁通值来给出相应网格点上磁通的程序。

用固定边界求解时，TEQ输出的磁面上点的坐标是很有规律的，当把这些点的坐标变换到以磁轴为极点的极坐标时，发现它们对应的极角的分布都是固定的，相同极角的点从磁轴处向外辐射至边界处，这样的规律给计算带来了较大的方便。

可以先把磁面上点的坐标从直角坐标转变为极坐标，如果要计算一个网格点（X，Y）上的磁通值，先把它变成极坐标（ρ，θ），然后找出该点邻近的2条辐射线L1和L2，其中L1上的点对应的角为θ1，L2上的点所对应的角为θ2，θ1和θ2满足θ1≤θ＜θ2。

在L1上找出P1（ρ1，θ1）、P2（ρ2，θ1），使ρ1≤ρ＜ρ2，再在L2上找出P3（ρ3，θ2）、P4（ρ4，θ2），使ρ3≤ρ＜ρ4，依次在L1和L2上进行样条插值得出ρ处的磁通值，然后再根据该网格点到L1和L2的距离进行对距离的加权平均，这样就可以得到其磁通值了。对于边界处的点，先判断该点在边界内还是边界外，在边界内就用上面的方法来计算。边界外的点，由于不能确定其磁通值具体是多少，而且在计算中也不需要知道边界外的网格点的磁通值具体是多少，因此，统一设为比边界处的磁通值略小的值即可。

算法流程如图2所示，用此方法算出的gfile画最外闭合磁面时，会出现不光滑的现象，但对内部的闭合磁面基本没有影响，可以通过增加网格点的数量来降低最外磁面不光滑的程度。

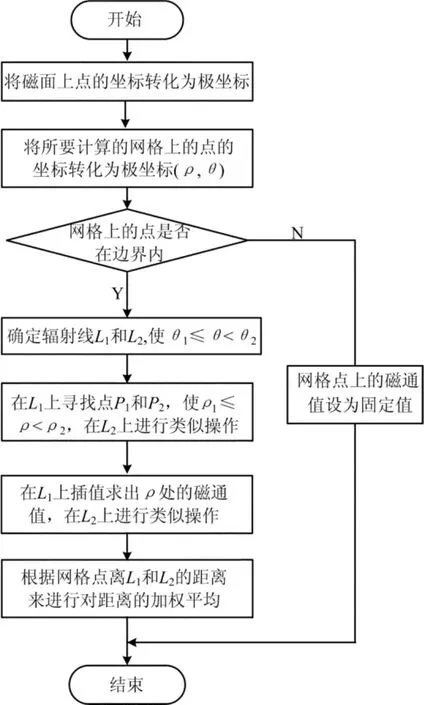
图2 修正磁面位形的程序流程

4 计算结果对比

本文以EFIT计算出的剪切及反剪切情况的g－file作为数据来源。以反剪切情况为例，安全因子分布如图3中虚＊线所示，其中，横坐标为归一化的ψ。

图3 反剪切情况下的安全因子分布

压强分布如图4中虚＊线所示，此种情况下，用EFIT－viewer画出的平行于磁场方向的电流，如图5中虚＊线所示，等离子体电流为1.05MA。在TEQ中用这样的安全因子和压强分布进行计算，得到的安全因子分布如图3中实线所示，压强分布如图4中实线所示，平行电流分布如图5中实线所示，等离子体电流为1.05MA，磁面位形如图6所示，其中虚＊线表示求解固定边界时设定的边界。由于TEQ采用固定边界求解，在边界以外的区域没有进行求解，因此，也就无法直接得到边界以外的磁面位形。可以看到反剪切情况下，由EFIT和TEQ得到的安全因子、压强分布符合较好，平行电流分布也基本相同。通过比较，磁面位形也相同。另外，对剪切情况进行计算，可以得出相同的结论。

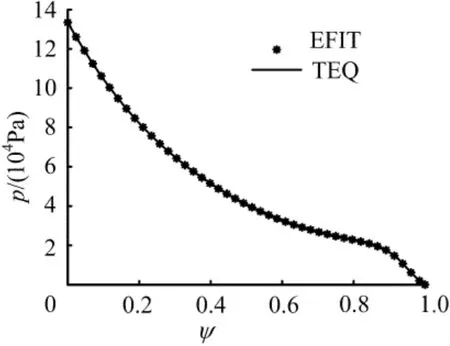
图4 反剪切情况下的压强分布

图5 反剪切情况下平行电流分布

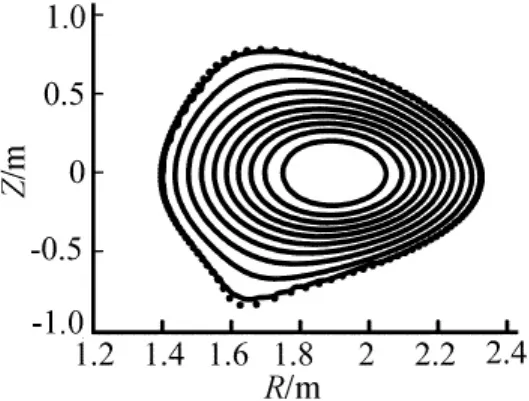
图6 反剪切情况下TEQ计算出的磁面位形

5 构建反剪切平衡位形

TEQ可以直接利用安全因子和压强来进行平衡的构建，这对设计新的托卡马克具有较大意义，可以方便地调节安全因子分布和压强分布，从而获得想要的磁面位形，比用EFIT方便。由于反剪切可以使等离子体性能大大改善，因此对先进托卡马克而言，反剪切是一种吸引人的选择，所以用图3中的安全因子分布、图4中压强分布分别乘以因子 0.50、0.75、1.00、1.25、1.50、1.75后，得到的一组压强分布作为输入来构建固定边界平衡，得到6组不同平衡参数，见表1所列［10－11］。以这种方式计算大量数据后，可以为构建需要的平衡提供一种参考依据。

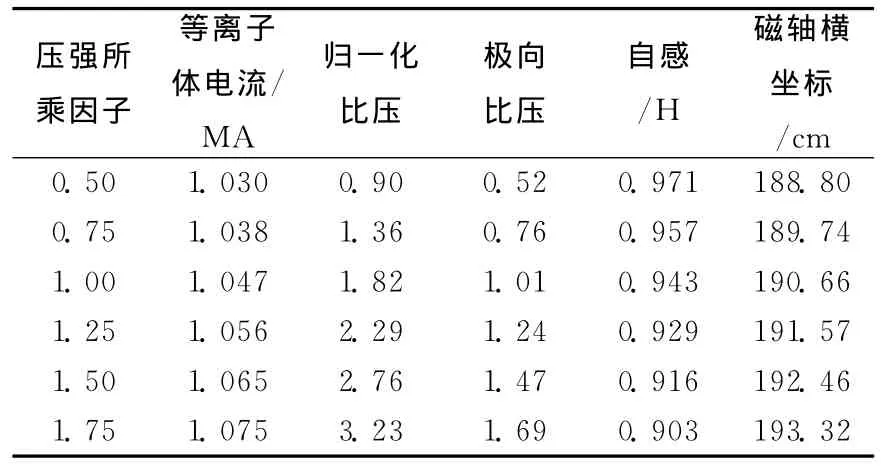
表1 6组反剪切平衡参数

由表1可以看出，随着压强的变大，磁轴横坐标变大，表明压强变大时，磁轴向外侧移动，而且压强越大，磁轴移动得越多。

这可以定性解释为：在托卡马克中，磁力线的平衡由指向内侧的磁张力和指向外侧的磁压力、向外的压力（由气体压强梯度产生）等来提供。在计算中，未改变磁场的大小，因此，磁压力的影响可以忽略，而当压强等比例增大时，压强梯度也变大，这样向外的压力就会增大，这只有依靠变大的磁张力来产生，而这就要求磁力线发生更大的形变来提供，于是便产生了上面的结果。

6 结束语

本文对TEQ输出g－file的程序进行了修正，使得计算出的安全因子、压强、F、平行方向电流的分布以及磁面位形都能与EFIT符合得非常好。通过对剪切和反剪切2种情况的检验，可以认为在TEQ基础上增加的读取g－file，并进行固定边界求解的功能得到了比较好的实现。

利用TEQ，可以方便地在知道安全因子分布和压强分布的情况下，进行平衡的构建，这对于设计期望的磁面位形具有重要意义。另外，从研究压强对磁轴水平位置的影响发现，当压强变大时，磁轴向外移动，并且压强变得越大，磁轴移动得越多。

［1］Kritz A H，Bateman G，Kinsey J，et al.The national transport code collaboration module library［J］.Computer Physics Communications，2004，164（1／3）：108－113.

［2］Crotinger J A，Lo Destro L，Pearlstein L D，et al.Corsica：a comprehensive simulation of toroidal magnetic－fusion devices［EB／OL］.（1997－06－12）［2011－10－19］.http：／／wormhole.ucllnl.org／software／corsica／finalreport.pdf.

［3］Carlsson J，Tech－X Corporation.TEQ library user manual［EB／OL］.（2007－07－31）［2010－10－15］.http：／／w3.pppl.gov／ntcc／Teq／TEQmanual.pdf.

［4］Carlsson J，Tech－X Corporation.Separatrix library user manual［EB／OL］.（2006－01－14）［2010－10－18］.http：／／w3.pppl.gov／ntcc／Separatrix／SeparatrixManual.pdf.

［5］Ferron J R，Walker M L，Lao L L，et al.Real time equilibrium reconstruction for tokamak discharge control［J］.Nuclear Fusion，1998，38（7）：1055－1066.

［6］胡希伟.等离子体理论基础 ［M］.北京：北京大学出版社，2006：23－69.

［7］查学军，朱思铮，虞清泉.托卡马克等离子体平衡的数值研究 ［J］.计算物理，2002，19（5）：413－418.

［8］Degtyarev L M，Drozdov V V.An inverse variable technique in the MHD－equilibrium problem ［J］.Computer Physics Reports，1985，2（7）：341－387.

［9］Bulmer R H，Pearlstein L D.DIII－D equilibrium and stability modeling with Caltrans［EB／OL］.（2003－01－28）［2010－10－15］.http：／／wormhole.ucllnl.org／software／corsica／d3d－demo.pdf.

［10］邱励俭.聚变能及其应用 ［M］.北京：科学出版社，2008：152－153.

［11］程曹军，肖炳甲，刘成岳.基于Corsica的EAST等离子体平衡计算 ［J］.合肥工业大学学报：自然科学版，2011，34（4）：613－616.

Simulation of fixed－boundary tokamak plasma equilibrium with TEQ

LIU Zhi－yuan， LI Guo－qiang， XU Li－qing
（Institute of Plasma Physics，Chinese Academy of Sciences，Hefei 230031，China）

A new calculation process of TEQ is designed.An algorithm to calculate magnetic fluxes on grid points with positions of magnetic surfaces and corresponding values of the magnetic fluxes is developed.And the program of outputting g－file is improved for solving the fixed－boundary tokamak plasma equilibrium with TEQ.Based on the EAST device，two groups of safety factor and pressure profile which denote shear and reverse shear respectively are used to test the program.It is shown that the result of TEQ coincides with that of EFIT very well.Finally，six reverse shear fixed－boundary equilibriums are constructed and the effect of pressure on the horizontal coordinate of magnetic axis is analyzed.

TEQ program；g－file program；EAST device；fixed－boundary plasma equilibrium；numerical simulation

O539

A

1003－5060（2012）03－0412－05

10.3969／j.issn.1003－5060.2012.03.028

2011－09－14；

2011－10－25

国家自然科学基金资助项目（10975161）；科技部ITER专项课题资助项目（2009GB01001）

刘志远（1988－），男，山东济宁人，中国科学院等离子体物理研究所硕士生；

李国强（1977－），男，河南杞县人，博士，中国科学院等离子体物理研究所副研究员，硕士生导师.

（责任编辑 吕 杰）