一个多介质流体的Baer－Nunziato修正模型及其Lax－Wendroff格式

吴 强， M.A.乌拉赫

（1.上海大学 数学系，上海 200444；2.合肥工业大学 数学学院，安徽 合肥 230009；3.吉大港大学 数学系，吉大港 4331，孟加拉国）

一个多介质流体的Baer－Nunziato修正模型及其Lax－Wendroff格式

吴 强1，2， M.A.乌拉赫3

（1.上海大学 数学系，上海 200444；2.合肥工业大学 数学学院，安徽 合肥 230009；3.吉大港大学 数学系，吉大港 4331，孟加拉国）

文章在BN模型基础上，提出了一个描述可压缩多介质流体的介质界面的修正模型，并且给出了该模型的具有二阶精度的Lax－Wendroff格式。无论模型和格式，都保证了总质量和分质量守恒、总动量和总能量守恒。更重要的是它消除了速度和压力在介质界面处的伪振荡，数值算例表明这一算法是有效的。

守恒律；多介质流；伪振荡；Lax－Wendroff格式

可压缩多介质流体流动的模拟及其数值方法是近年来计算流体力学中的一个研究热点［1－2］。该问题在流体力学、材料科学、天体力学以及武器物理、惯性约束聚变（ICF）、载人航天与探月工程等前沿科学领域和国家重大工程中有着广泛而重要的应用背景和实际意义。

多介质流体流动的模拟存在许多困难，其中最主要的困难是如何建立数学模型，以及由该模型所建立的数值方法可能造成速度和压力在介质界面附近的伪振荡［1，3－4］。

文献［2］提出了一个双密度、双速度和双压力的模型，然而该模型过于复杂难以用于实际计算。人们提出了许多简化或修正模型［5－7］，但这些模型依然无法消除多介质流体，特别是强激波情况下，速度和压力在介质界面附近的伪振荡。本文同样对BN模型［2］进行简化和修正，提出了多介质流体模型。

1 数学模型

本文以2种流体为例，提出多介质流体的数学模型，即在整个一维空间x轴方向上流动着2种流体，其形式为：

其中，ρ1、ρ2分别表示2种流体的密度；ρ为总密度；u为流体的速度；p为流体的压力；ρ1E1、ρ2E2分别为2种流体的能量。

此外，本文也采用了组份模型方程来描述物质界面的演化过程，即

其中，0≤α≤1。然而，和BN模型不同的是这里的组份α是用来计算总压力的，即

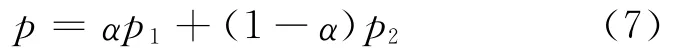
其中，p1、p2分别表示2种流体的压力，且分别具有状态方程，即

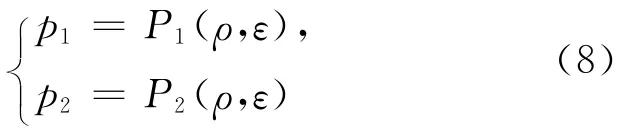
且满足：

这样，（1）～（7）式构成了多介质流体流动的数学模型，可以把（1）～（6）式写成矢量形式，即

其中

定理1 数学模型（1）～（7）式满足流体的分质量守恒、总质量守恒、总动量守恒和总能量守恒。

证明 （1）式、（2）式分别表明2种流体的分质量守恒；将（1）式和（2）式相加，可以得到流体总质量守恒；（3）式表明流体的总动量守恒；将（4）式和（5）式相加，可以得到流体总能量守恒。证毕。

定理2 数学模型（1）～（7）式是双曲型的。

证明 可以将方程组（9）式改写成非守恒量W＝（ρ1，ρ2，u，p1，p2，α）的拟线性形式，即

很容易得到A（W）的特征值为：

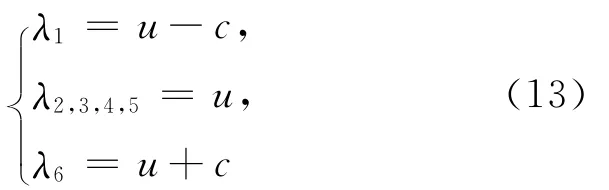
其中（14）式为流体声速，即

这样，由ρ1、ρ2、p和α的非负性和（8）式可得c为实数，即数学模型是双曲型的。

针对多流或多相流的数值模拟中速度和压力会出现伪振荡，文献［9］提出了关于模型及其离散形式有效性的一个准则，即“一个两相流体，其速度和压力如果在初始时刻是一致的，那么随着时间发展，它们依然是一致的”，称之为UPV（uniform in pressure and velocity）准则；同时指出，产生速度和压力的伪振荡的原因，就是这些模型及其数值方法破坏了UPV准则。下文给出的模型能够消除速度和压力在介质界面处的伪振荡的原因，就是模型满足该准则。

定理3 模型（1）～（7）式满足UPV准则。

证明 假设一多介质流体的初始速度和压力分别为常数，u（x，0）≡u0和p（x，0）≡p0。

（1）将（1）式、（2）式代入（3）式，可得：

（2）由（11）式可得p1和p2的发展方程，将2个方程相加，可得：

（3）由u和p的初值，可得（15）式、（16）式的唯一解，分别为u（x，t）≡u0和p（x，t）≡p0。证毕。

2 数值方法

采用文献［4］的方法，给出模型（1）～（6）式二阶精度的Lax－Wendroff格式，即

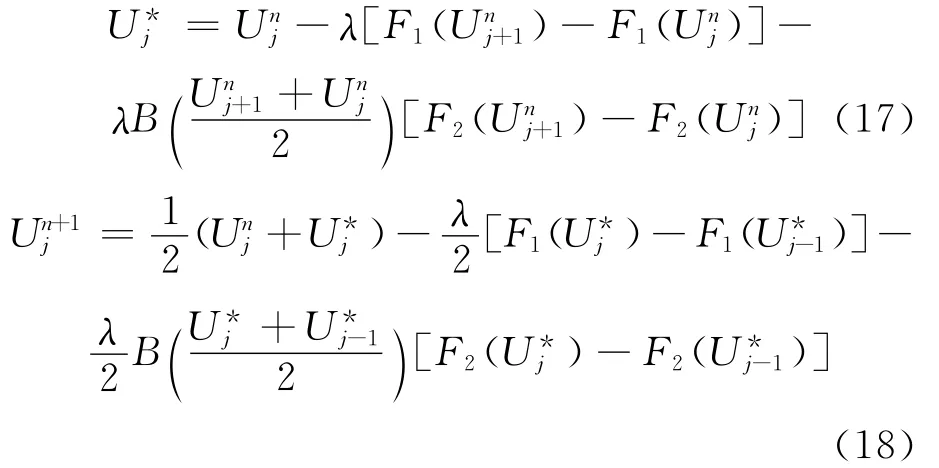
其中，j为空间网格；n为时间网格；λ＝τ／h；h为空间步长；τ为时间步长，并且满足如下CFL条件：

其中，c为流体声速。网格上总压力计算为：

分压力为：

如果将（17）式、（18）式写成分量形式，并且和定理1的证明类似，则很容易得到如下定理。

定理4 当CFL条件（19）式成立时，（17）式、（18）式满足分质量守恒、总质量守恒、总动量守恒和总能量守恒。

配电网N-1安全性准则是配电网规划和运行的重要准则，它规定了在配电网中主变压器或线路发生故障时，线路或主变压器所带负荷可通过与之联络的线路进行转供，即不对外停电。

定理5 （17）式、（18）式满足 UPV准则。

3 数值算例

通过2个算例来验证（17）式、（18）式在数值模拟多介质流体流动的有效性，其中实线代表通过求解Riemann问题的精确解，点代表Lax－Wendroff格式的数值解。

算命1 考虑不同理想气体的激波管问题，初始间断在x＝0.5位置，初值如下：

当0＜x＜0.5时，ρ1＝1.0，u1＝0，p1＝1.0，γ1＝1.6，α＝1.0；当0.5＜x＜1.0时，ρ2＝0.125，u2＝0，p2＝0.1，γ2＝1.2，α＝0。

本算例选自文献［1］，这是著名的Sod激波管问题，很多流体力学计算的论文都用它来验证自己的计算格式，理想气体的状态方程为p＝（γ－1）ρε。

算例2 考虑stiff气体和van der Waals气体的激波管问题，初始间断在x＝1位置，初值如下：

当0＜x＜1时，ρ1＝103，u1＝0，p1＝109，γ1＝4.4，π＝6×108，α＝1；当1＜x＜2时，ρ2＝50，u2＝0，p2＝105，γ2＝1.4，a＝5，b＝10－3，α＝0。

图1 算例1的计算结果

在区间［0，2］上，网格区间数为1 000，时间为0.000 24时的总密度、速度、总压力和总能量的计算结果［11］，如图2 所示。

本算例中左边stiff气体的π＝6×108，a＝5，b＝10－3，表明是刚性气体，相当于液体，而且两边压力很大，为强激波。计算结果表明，对于此数值算例，速度和压力的数值解和精确解也是非常吻合的。

图2 算例2的计算结果

4 结束语

本文提出了BN模型的一个简化和修正模型，并采用文献［4］的方法给出了该模型的具有二阶精度的Lax－Wendroff格式，该模型是双曲型的，而且无论模型和格式都保证了总质量和分质量守恒、总动量和总能量守恒。数值算例表明它有效地模拟可压缩多介质流体的介质界面的运动，更重要的是它能有效地消除多介质流体，特别是强激波情况下，速度和压力在介质界面处的伪振荡。

［1］Abgrall R，Karni S.Computation of compressible multifluid［J］.Journal of Computational Physics，2001，169：594－623.

［2］Baer M R，Nunziato J W.A two－phase mixture theory for the deflagration－to－detonation transition（DDT）in reactive granular materials［J］.International Journal of Multiphase Flow，1986，12：861－889.

［3］Chargy D，Abgrall R，Fezoui L，et al.Comparison of several upwind schemes for multicomponent one－dimensional inviscid flows［R］.INRIA report，1253，1990.

［4］MacCormack R W.The effect of viscosity in hypervelocity impact cratering［J］.Journal of Spacecraft and Rockets，1969，40（5）：757－763.

［5］Allaire G，Clerc S，Kokh S.A five－equation model for the simulation of interfaces between compressible fluids［J］.Journal of Computational Physics，2002，181：577－616.

［6］Berthon C，Nkonga B.Multifluid numerical approximations based on a multipressure formulation［J］.Computers and Fluids，2007，36：467－479.

［7］Saurel P，Petitpas F，Berry R A.Simple and efficient relaxation methods for interfaces separating compressible fluids，cavitating flows and shocks in multiphase mixtures［J］.Journal of Computational Physics，2009，228：1678－1712.

［8］Fedkiw R，Aslam T，Merriman B，et al.A non－oscillatory Eulerian approach to interfaces in multimaterial flows（the Ghost Fluid Method）［J］.Journal of Computational Physics，1999，152：457－492.

［9］Saurel P，Abgrall R.A multiphase Gogunov method for compressible multifluid and multiphase flows［J］.Journal of Computational Physics，1999，150：425－467.

［10］Shyue K M.A fluid－mixture type algorithm for compressible muilticomponent flow with van der Waals equation of state［J］.Journal of Computational Physics，1999，156：43－88.

［11］沃恒洲，姚智华，王国丰，等.发动机喷嘴内部空化流动的数值模拟研究［J］.合肥工业大学学报：自然科学版，2011，34（5）：651－654，670.

A modified Baer－Nunziato model of multifluid flow and its Lax－Wendroff scheme

WU Qiang1，2， M.A.Ullah3
（1.Dept.of Mathematics，Shanghai University，Shanghai 200444，China；2.School of Mathematics，Hefei University of Technology，Hefei 230009，China；3.Dept.of Mathematics，Chittagong University，Chittagong 4331，Banglandesh）

This paper proposes a modified Baer－Nunziato model and its Lax－Wendroff scheme with the second order accuracy for the simulation of material interface of different compressible multifluid flow.Both the model and the scheme fully guarantee the total and individual mass conservation as well as the total momentum and total energy conservation.And the spurious oscillation of velocity and pressure across the material interface is eliminated.Numerical examples verify the effectiveness of the algorithm.

conservation law；multifluid flow；spurious oscillation；Lax－Wendroff scheme

O241.82

A

1003－5060（2012）03－0417－04

10.3969／j.issn.1003－5060.2012.03.029

2011－06－25；

2011－08－12

国家自然科学基金资助项目（10971132）；安徽省自然科学基金资助项目（11040606M06）

吴 强（1973－），男，安徽芜湖人，上海大学博士生，合肥工业大学讲师.

（责任编辑 吕 杰）