B样条曲线曲面的一种光顺算法

秦贤杰， 黄有度

（合肥工业大学 数学学院，安徽 合肥 230009）

B样条曲线曲面的一种光顺算法

秦贤杰， 黄有度

（合肥工业大学 数学学院，安徽 合肥 230009）

文章给出了一种新的B样条曲线曲面光顺算法，该算法以型值点的变动量为未知量，以型值点变动量的变动范围为约束条件，给出能量函数；通过遗传算法对能量函数最小化求解，直接得到光顺后的新的型值点；最后给出实例，表明该B样条曲线曲面光顺算法是一种有效的光顺算法。

B样条；曲面；遗传算法；光顺；能量函数

在工业设计和反求工程中，B样条曲线曲面是一种进行形状设计和数据拟合的重要工具［1］。B样条曲线曲面的光顺性对最终产品外观有着直接影响。光顺处理包括曲线、曲面的光顺性检查和光顺准则制定以及曲线、曲面的修正，现将分别讨论这3个问题。国内外已有大量文献研究曲线曲面的光顺问题，但以型值点作为优化变量的文献较少。文献［2－3］用应变能最小作为光顺准则，加上约束条件对曲线曲面进行局部光顺，其最优化变量为曲线曲面的控制顶点。文献［4－6］将控制顶点作为优化变量，尽管其光顺准则有所不同。以控制顶点为优化变量的光顺方法，曲线曲面光顺后仍需曲线曲面与直线求交，然后求得光顺后型值点。与现有方法相比，本文方法直接以型值点变动量作为优化变量，光顺后直接得到型值点的变动量及新的型值点，这在船舶型线放样中有较强的实用性。

1 B样条曲线的光顺

1.1 曲线的光顺性检查

在实际工作中，经常会要求根据给定的型值点用样条攀成一条经过这些型值点的曲线，即数学中所说的按顺序插值型值点生成相应曲线。设给定型值点Q0，Q1，…，Qn，本文用3次B样条曲线按顺序插值这些型值点［7］。型值点的参数化为累加弦长参数化，即令：

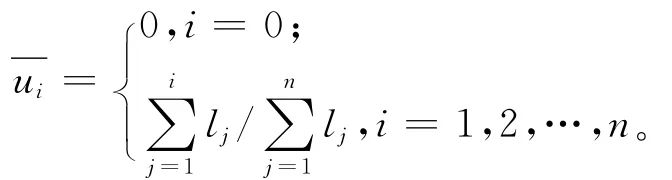
其中，li＝｜Qi－1Qi｜。设U＝｛u0，u1，…，un＋6｝＝｝为3次B样条的节点空间。B样条基函数的递推公式为：

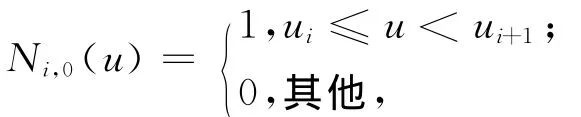
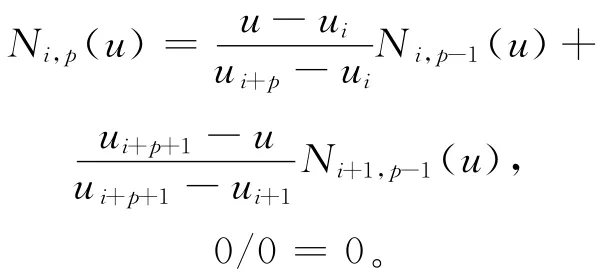
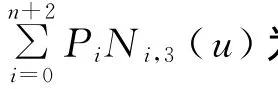
现在检查各型值点Qi（即P））附近的曲率变化情况，P（）附近曲率变化记作ΔK）。令，其中，i＝1，2，…，n－1。K（u）为3次B样条曲线P（u）的曲率，令

P）附近曲率变化）作为曲线光顺性的检查。大者说明型值点）点附近曲率变动大，相反，小者说明型值点点附近曲率变动小。此处认为小者附近曲线比大者附近曲线更为光顺。找出 max｛，i＝1，2，…，n－1｝，假设为，则将Qj、Qj－1、Qj＋1作 为 待 光 顺 的型值点。

1.2 曲线的光顺准则

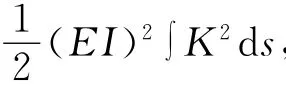
1.3 曲线的光顺算法

算法的基本步骤如下：

（1）找出“瑕点”，即型值点中型值点附近曲率变化最大的型值点。设max｛ΔK（），i＝1，2，…，n－1｝为 ΔK（），则Qj即为所对应的“瑕点”。

（2）将Qj、Qj－1、Qj＋1作为待修改的型值点。

（3）给定修改约束，设为新型值点，Δj＝｜－Qj｜≤ε，ε为给定的约束范围。

（4）利用基本遗传算法求解新型值点、

遗传算法求解步骤如下［9］：

（1）设型值点Qj、Qj－1、Qj＋1的变动量Δj、Δj－1、Δj＋1为 基 因，种 群 数 为 30，进 化 代 数为1 000。

（2）令＝Qj＋Δj；＝Qj－1＋Δj－1；，重新插值生成经过新型值点的3次B样条曲线，将作为适应度函数。

（3）经过选择、交叉、变异等操作后，终止进化，最终得到型值点的变动量Δj、Δj－1、Δj＋1及新的型值点，即：＝Qj＋Δj，＝Qj－1＋Δj－1，

（4）插值新型值点生成光顺后的3次B样条曲线。

（5）判断是否继续修改曲线，此时既可以设定为人工判断，也可以设定为计算机自动根据条件完成判断。

1.4 曲线光顺效果

图1所示为某工程船型线图中1条站线的部分曲线图，图2所示为带有噪声的曲线图，图3所示为用本文算法对图2进行3次光顺后的曲线图。可以看出本文曲线光顺算法十分有效。图1～图3中上方为曲线上离散点的曲率图。

2 B样条曲面的光顺

2.1 曲面的光顺性检查

对曲面的光顺一般可以转化为对曲面的网格曲线或曲面的u、v方向参数曲线的光顺。本文将曲面的光顺转化为对曲面的网格曲线的光顺。给定型值点列｛Qi，j｝，i＝0，1，…n，j＝0，1，…，m。根据上述插值曲线的方法，可以生成2组曲线，一组以｛Qi，j｝每一横列的m＋1个型值点生成n＋1条3次B样条曲线组，此处称为水线组；另一组以｛Qi，j｝每一竖列的n＋1个型值点生成m＋1条3次B样条曲线组，此处称为站线组。

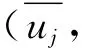
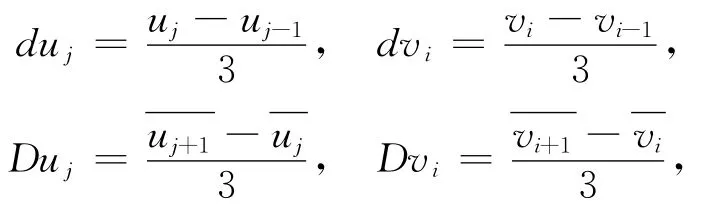
其中，i＝1，2，…，n－1；j＝1，2，…，m－1；K（u）为3次B样条曲线P（u）的曲率，令

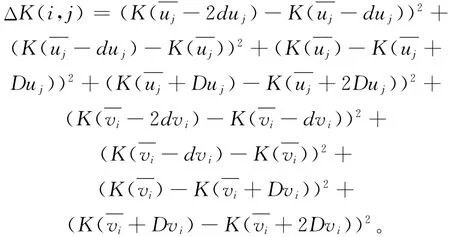
Qi，j附近网格曲线的曲率变化ΔK（i，j）作为网格曲线光顺性的检查。ΔK（i，j）大者说明型值点Qi，j点附近网格曲率变动大；ΔK（i，j）小者说明型值点Qi，j点附近网格曲率变动小。ΔK（i，j）小者附近网格曲线比ΔK（i，j）大者附近网格曲线更为光顺。找出 max｛ΔK（i，j），i＝1，2，…，n－1；j＝1，2，…，m－1｝，假设为 ΔK（i，j），则 将Qi，j、Qi－1，j、Qi＋1，j、Qi，j－1、Qi，j＋1作为待光顺的型值点。

2.2 曲面的光顺准则

曲面光顺过程中，可以将∬Ω＋）dΩ作为曲面光顺程度的判定［5］，其中，k1、k2为曲面的主曲率。本文按照上述曲线光顺中的方法，将2组B样条曲线组的应变能总和最小作为光顺准则，，其中，Wi为第i＋1条站线的应变能；Vj为第j＋1条水线的应变能，其求法与上文相同。

2.3 曲面的光顺算法

算法的基本步骤如下：

（1）找出“瑕点”，即型值点列中型值点附近网格曲率变化最大的型值点。max｛ΔK（i，j），i＝1，2，…，n－1，j＝1，2，…，m－1｝，设为 ΔK（i，j），则Qi，j即为所对应的“瑕点”。

（2）将Qi，j、Qi－1，j、Qi＋1，j、Qi，j－1、Qi，j＋1作为待修改的型值点。

（3）给定修改约束，设为新型值点，Δi，j＝≤ε，ε为给定的约束范围。

（4）利用基本遗传算法求解新型值点、

遗传算法求解步骤如下：

（1）设型值点Qi，j、Qi－1，j、Qi＋1，j、Qi，j－1、Qi，j＋1的变动量Δi，j、Δi－1，j、Δi＋1，j、Δi，j－1、Δi，j＋1为基因，种群数为30，进化代数为1 000。

（2）令＝Qi，j＋Δi，j，＝Qi－1，j＋Δi，j－1，＝Qi，j＋1＋Δi，j＋1，重新插值生成经过新型值点的3次B样条曲线网格，将作为适应度函数。

（3）经过选择、交叉、变异等操作后，终止进化，最终 得 到 新 的 型 值 点 的 变 动 量Δi，j、Δi－1，j、Δi＋1，j、Δi，j－1、Δi，j＋1及新型值点，即

（5）插值新型值点生成光顺后的3次B样条曲线网格。

（6）判断是否继续修改曲线网格，此时既可以设定为人工判断，也可以设定为计算机自动根据条件完成判断。

（7）根据光顺后的型值点及B样条曲线网格，用蒙皮法生成B样条曲面。

2.4 曲面光顺的效果

图4所示为某工程船部分水线、站线网格图。

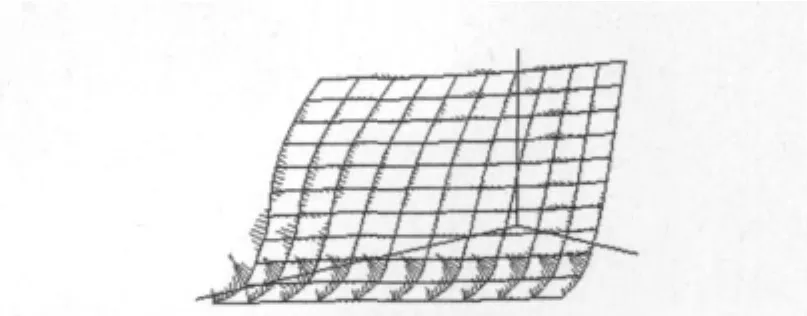
图4 水线、站线网格

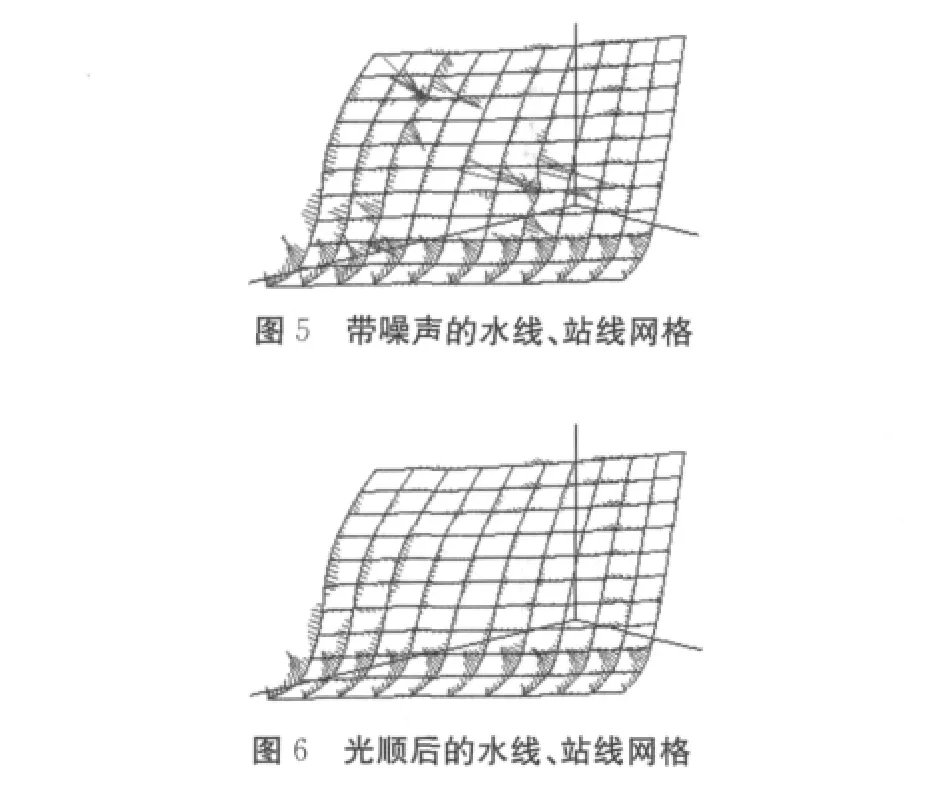
图5所示为带有噪声的网格图，图6所示为用本文算法对图5进行10次光顺后的网格图。从中可以看出本文算法是十分有效的。

3 结束语

本文提出了一种新的B样条曲线曲面的光顺算法，以型值点的变动量为未知量，以型值点变动量的变动范围为约束条件，给出能量函数，通过遗传算法对能量函数最小化求解，直接得到光顺后的新的型值点。该算法的优点在于以型值点变化量作为变量，光顺处理后直接得到光顺后的型值点，这在船舶放样等工业工程中有较强的实际应用。本文的不足之处在于，给定的修改约束ε过大或过小将影响光顺效果。ε过大则光顺后的曲线趋于平缓，ε过小则光顺的次数需增加。通过实例，可以看出本文算法是十分有效的。

［1］席 平，刘 勇.反向工程中的曲面光顺算法［J］.北京航天航空大学学报，2002，28（2）：125－128.

［2］Zhang Caiming，Zhang Pifu，Cheng Fuhua.Fairing spline curves and surfaces by minimizing energy［J］.Computer－Aided Design，2001，33：913－923.

［3］Liu Yujun，Zhu Xiuli，Ji Zhuoshang.Ship hull plate processing surface fairing with constraints based on B－spline［J］.Journal of Marine Science and Application，2005，4（3）：13－17.

［4］屠 静，檀结庆.参数3次B样条曲线的一种局部光顺方法［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2009，32（4）：568－571.

［5］Sari¨oz E.An optimization approach for fairing of ship hull forms［J］.Ocean Engineering，2006，33：2105－2118.

［6］Pérez－Arribas F，Suárez－Suárez J A，Fernández－Jambrina L.Automatic surface modeling of a ship hull［J］.Computer－Aided Design，2006，38：84－594.

［7］Piegl L，Tiller W.The NURBS book（2ndEdition）［M］.2nd ed.New York：Springer，1997：371－375.

［8］仵大伟，林 焰，纪卓尚.船体曲线曲面的B样条光顺［J］.中国造船，2002，43（4）：90－94.

［9］王小平，曹立明.遗传算法：理论、应用与软件实现［M］.西安：西安交通大学出版社，2002：18－50.

A kind of fairing method for B－spline curves and surfaces

QIN Xian－jie， HUANG You－du
（School of Mathematics，Hefei University of Technology，Hefei 230009，China）

In this paper，a new fairing method for B－spline curves and surfaces is presented.Taking the variation of points as the unknown and the range of the variation as the constraint，this method obtains new faired points after defining the energy function and minimizing the energy function with genetic algorithm.The examples given in the paper show the effectiveness of the method.

B－spline；surface；genetic algorithm；fairing；energy function

TP391.411

A

1003－5060（2012）03－0429－04

10.3969／j.issn.1003－5060.2012.03.032

2011－05－31；

2011－07－06

秦贤杰（1986－），男，安徽安庆人，合肥工业大学硕士生；

黄有度（1949－），男，广西贺县人，合肥工业大学教授，硕士生导师.

（责任编辑 张 镅）