冷弯薄壁方钢管梁柱加腋节点抗震性能研究

张春涛，李正良，2，王汝恒，贾 彬，

(1.重庆大学 土木工程学院，重庆 400045;2.重庆大学 山地城镇建设与新技术教育部重点实验室，重庆 400045;3.西南科技大学 土木工程与建筑学院，绵阳 621010)

上世纪90年代初期，Northridge和Kobe大地震中钢框架梁柱的传统焊接节点产生了大量脆性破坏。梁柱连接焊缝出现脆性断裂或脆性裂纹，而节点钢梁却尚未出现塑性变形，未达到预期的抗震设计要求，抗震可靠性能受到了广泛质疑［1－4］。为此，在震后研究中减小梁柱焊缝应力改善节点区域延性性能，迫使钢梁出现塑性铰，成为改善节点抗震设计的重要思路。

局部削弱梁截面或在梁端焊接加劲腋板迫使节点梁产生塑性铰是改善节点延性的两种重要方法。其中加腋节点由于既能在提高节点抗弯强度的同时，又能有效改变节点梁的剪力转移机理，降低结构对节点焊缝韧性的要求，迫使节点梁产生塑性铰，充分发挥其塑性耗能性能，获得了广泛关注。美国SAC Joint Venture［5］通过试验对不同规格的梁柱加腋节点进行了研究，试件最大塑性铰达到了0.05 rad，试验结果良好，为此SAC委员会提出了梁柱加腋节点不同形式的细部构造。Uang等［6］在对四个足尺试件进行静、动力试验的基础上，提出了加腋节点地震响应的简化计算模型，但该模型假设了节点柱弯曲状态应力按线性分布;并利用往复加载试验对梁柱加腋节点和局部削弱梁截面的改进节点进行了滞回性能研究，通过对不同工况下两类节点的6个试件进行对比分析，发现加劲腋板有效改善了节点的滞回性能，提高了节点梁塑性变形的能力［7］，但该试验中仅对梁端下翼缘进行了加腋处理，导致个别试件节点梁上翼缘出现了脆性破坏。Yu等［8］通过试验得到了加劲腋板能明显改善节点梁的剪力传递机理，提出了节点梁翼缘焊缝应力水平的简化计算模型，该模型能够同时考虑节点梁和加劲腋板之间的相互作用力和变形能力。Lee等［9］对加腋节点的延性及破坏特征进行了详细研究。

综上所述，不难发现上述学者均是对普通钢框架结构的梁柱加腋节点进行了相关研究，为此领域打下了良好基础。但关于冷弯薄壁钢管梁柱加腋节点的研究尚少，限制了冷弯薄壁构件在抗震地区的应用。2008年汶川地震后，冷弯薄壁型钢焊接节点在灾区重建中被广泛采用(如图1所示)。但冷弯薄壁型钢构件壁厚仅1～3mm，强度质量比高，焊接连接应用少，梁柱节点连接方式及力学性能还有待进一步研究。为此，本文依据“强柱弱梁”的抗震设计思想和控制塑性铰位置的思路［10］，在梁端加设了加劲腋板。并利用低周往复加载试验及有限元数值分析，对不同轴压比下普通节点和加腋节点的8个足尺试件进行了研究，通过对比分析讨论了两类节点的破坏模式、滞回性能，延性及耗能性能等。

图1 冷弯薄壁型钢梁柱节点Fig.1 Connection of cold-formed thin-walled steel structure

1 试验概况与加载制度

1.1 试件设计与制作

根据参考文献［10］的规定和参照实际钢结构工程，设计了两类节点试件，如图2所示。为了真实模拟循环荷载作用下梁柱节点在实际结构中的受力和变形特征，试件对梁柱节点的空间性以及节点间的相互作用进行了考虑，在两平面梁柱节点之间设置一纵向钢管梁，组成三维双节点空间模型。同时，为了通过对比分析，更好地研究加腋节点的抗震性能，钢管梁柱采用了不同的连接方式:图2(a)为普通节点J，纵横梁与钢管柱均采用普通焊接方式连接;图2(b)为加腋节点WJ，按“强节点，强锚固”的抗震设计原则，在普通节点J连接方式的基础上进行改进，两横梁上下翼缘与柱焊接处均增设垫板(120mm×100mm×3mm)和等边三角形腋板(100mm×3mm)，以达到增加节点的强度和变形能力，而纵梁与柱则直接焊接，与普通节点连接方式相同。

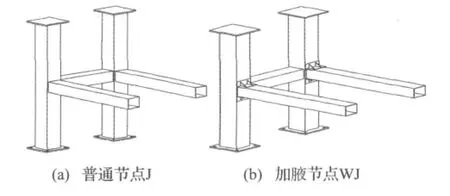
图2 节点构造Fig.2 Detail structure of connections

两类节点均采用足尺试件，钢管梁柱几何参数分别为:柱截面尺寸为120mm×120mm×3mm，柱高为1200mm;梁截面尺寸为100mm×100mm×2.0mm，跨度为800mm。钢管柱两端分别焊接截面尺寸为200mm×200mm×12mm的端板并加钻8个Φ18mm的栓孔，然后用4.8级M16高强螺栓与支座连接，试件梁柱连接焊缝用E43型焊条进行手工电弧焊焊接，试件成品如图3所示。同时，按照参考文献［11］的规定，在节点试件各构件中截取标准拉伸样坯，然后按照参考文献［12］的要求加工成材性试验试件。所有材性试验试件与梁柱节点试件同期加工，并按母材表面的处理方式对其进行抛丸除锈处理，材料力学性能指标见表1。与一般钢材相比，本次试验中弹性模量受钢材炼制工艺影响而偏小，为降低不同炉次的影响，各材性参数均为三个试件的平均值。

图3 梁柱节点试件Fig.3 Specimens of connection

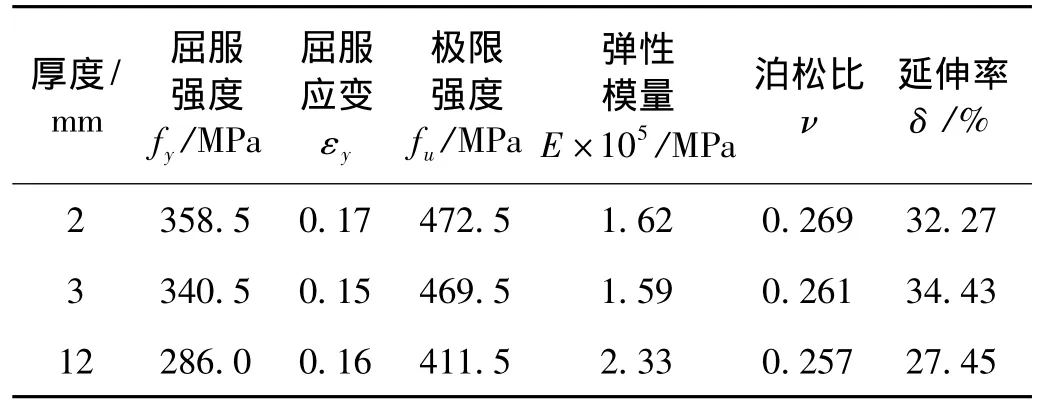
表1 材料力学性能指标Tab.1 Material characteristics of specimens

1.2 加载装置与测点布置

1.2.1 加载装置

试验中，因两类梁柱节点试件结构形式复杂，传统的MTS电液伺服加载系统尚不能满足要求。因此，按照参考文献［13］中几何可变式试验架的规定，项目组自行开发设计了一套改进加载试验系统，通过改进试验架的构造措施考虑了试件复杂的空间性，改进后加载装置如图4所示。

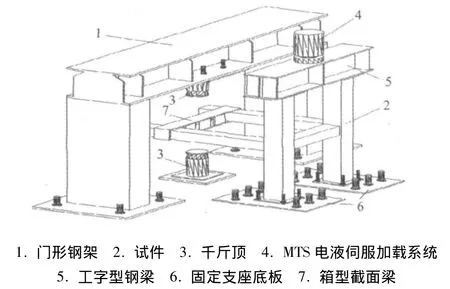
图4 试验改进加载装置图Fig.4 Detail diagram of improved test setup

1.2.2 测点布置

试件测点布置见图5，试验中共使用了7个位移计和3个百分表，位移计1～4用于测量横梁的变形，位移计5测量柱侧向位移，位移计6和7测量柱的平面内位移，其中以位移计4的测值作为施加往复荷载的控制位移Δ。同时，试件梁柱平面上布置64个测点，并通过四台DH3815应变采集箱采集应变数据，观察在往复荷载作用下节点区附近的梁柱翼缘应变的变化情况，了解两类节点的屈服与破坏机制。

图5 位移计布置Fig.5 Arrangement of displacementer

1.3 试验步骤与加载制度

根据参考文献［13］的规定，并结合本次试验自身的特点，采用荷载－位移双控加载制度对节点施加往复荷载，加载示意图如图6所示。试验加载步骤分为两个阶段:①根据方钢管柱的截面承载力，对两类节点各试件(普通节点 J试件编号:J－1、J－2、J－3、J－4;加腋节点 WJ试件编号:WJ－1、WJ－2，WJ－3、WJ－4)的柱子分别施加轴压比 0.2、0.4、0.6、0.8，对应的轴力分别为 120 kN、240 kN、360 kN、420 kN。②正式加载前为了消除构件安装缝隙、检查装置及仪表是否正常工作等，需进行预载。③正式加载时，首先按每级20 kN对钢管柱进行加载，直至预定轴压力为止。然后通过自平衡反力架上、下的千斤顶对横梁施加往复荷载。

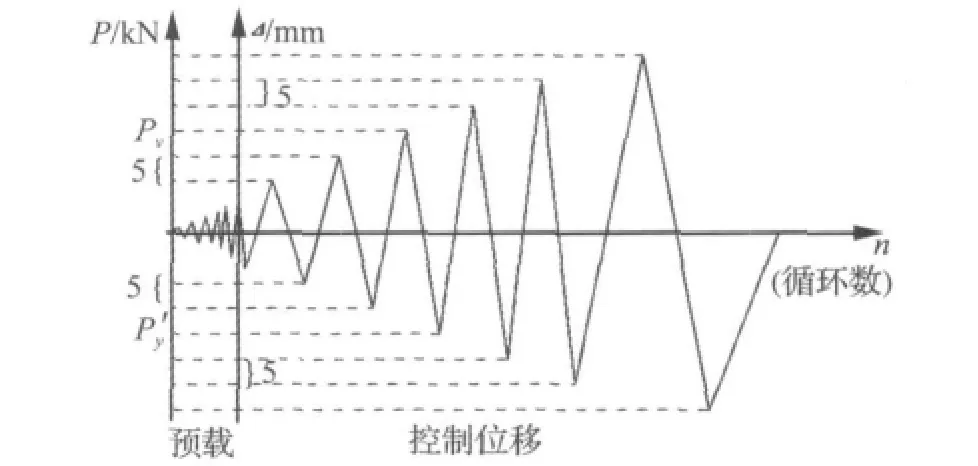
图6 荷载－位移双控加载制度Fig.6 The P－Δ double control loading system

2 实验现象及破坏模式

往复荷载作用下，两类节点以及同类节点的不同试件之间的试验现象和最终破坏模式均有明显差异。主要表现在:①轴压比对节点的破坏过程存在较大影响。轴压比为0.2和0.4时，两类节点均经历明显的弹塑性变形阶段，节点往复次数多，变形大;随轴压比增加到0.6和0.8时，荷载循环次数减少，节点脆性破坏特征明显增加;轴压比小于0.6时，与普通节点相比加腋节点受轴压比影响相对较小，节点承受循环荷载次数较多塑性变形充分;与加腋节点相比普通节点的破坏过程受轴压比影响较大。②节点最终破坏特征亦随轴压比不同而发生变化。轴压比小于0.6时，两类节点钢管梁柱协同变形能力较大，最终破坏时普通节点的柱棱角开裂较小且梁柱焊缝亦出现小裂纹，而加腋节点则为腋板边缘处梁壁出现屈曲，钢管柱棱角未出现裂纹;轴压比为0.6和08时，梁柱协同变形能力减小，普通节点最终破坏时钢管柱棱角开裂随轴压比增加而增大，加腋节点钢管梁局部屈曲变形增大。③加劲腋板对节点的受力和变形亦产生明显影响，致使相同轴压比下两类节点试件的最终破坏模式不同。如图7(a)～(d)所示，普通节点的最终破坏均是由钢管柱壁棱角开裂或梁柱连接焊缝拉裂引起。而加腋节点各试件的最终破坏则是钢管梁塑性变形过大出现局部屈曲，破坏模式如图7(e)～(h)所示。

加载过程中，控制位移Δ向下10mm时，不同轴压比下普通节点的钢管柱腹板出现最大压应变为1260 μξ，钢管梁的最大拉应变为410 μξ和最大压应变为488 μξ;但加腋节点的钢管柱出现最大压应变为1030 μξ，钢管梁的最大拉压应变分别为1313 μξ和1422 μξ。普通节点梁柱应变随轴压比增加呈先增加后减小的变化趋势，轴压比为0.2时达到最大值;加腋节点柱的压应变随轴压比呈线性增加，轴压比为0.8时达到最大值，而梁的拉压应变随轴压比亦呈先增后减变化，轴压比为0.4时才达到最大值。开始加载的几个往复循环过程中，两类节点均呈弹性状态，梁端残余变形小。随往复荷载增加，Δ为20mm时，普通节点的钢管柱棱角被拉裂，同时梁柱焊缝出现轻微裂纹，此时节点承载力随轴压比增加从19.23 kN减小到18.5 kN，部分应变片测值达到屈服应变1700 μξ;Δ为15mm时，加劲腋板边缘处梁下翼缘出现轻微向内凹陷，两则向外轻微鼓曲，此时节点承载力约为21.5 kN随轴压比变化较小，并且应变测值均小于屈服应变。Δ为25mm时，普通节点突然发出一声巨响，钢管柱棱角开裂，峰值位移处对应承载力小于上一循环，节点残余变形约为20mm随轴压比变化较小;该循环中加腋节点承载力继续增加，随轴压比增大从22.5 kN减小到19.2 kN，钢管梁屈曲变形加大，而残余变形却随轴压比增加从10mm增加到22mm，然后减小到13mm。Δ增加到40mm时候，普通节点的钢管柱棱角部位裂缝明显增大，承载力继续降低，节点域的部分应变片退出工作，而此时钢管梁的应变呈现减小变化趋势;不同轴压比下普通节点最终破坏形式为钢管柱棱角被拉裂，节点域的柱腹板屈曲，并且梁柱焊接裂缝开裂。加腋节点梁的变形速度随荷载往复运动加快，梁上部分应变片退出工作，而钢管柱上的应变片却仍处于弹性工作阶段，且承载力小于上个循环，此时梁的承载力已经进入下降阶段，节点最终破坏为钢管梁变形过大出现局部屈曲，但当轴压比为0.8时加腋节点试件的钢管柱棱角亦被拉裂。

图7 节点破坏模式Fig.7 Failure modes of connections

3 试验结果与分析

3.1 滞回性能分析

梁柱节点是罕遇地震作用下结构抗震性能的关键部位，只有了解了节点在低周往复荷载作用下的滞回性能才能正确评价其抗震能力。图8给出了两类节点在不同轴压比下的滞回曲线，对比分析可知:① 轴压比对两类节点的滞回曲线影响大，随轴压比增大节点脆性破坏特征增加，节点往复次数降低，滞回环环数明显减少而且逐渐趋于一条直线。对比图8(a)～(b)与图8(e)～(f)可见，轴压比小于0.4时，因加劲腋板增强了节点刚度，提高了节点的变形能力，致使加腋节点的滞回环数较普通节点多且形状饱满，钢管梁的塑性变形性能得到了充分发挥;当轴压比增加到0.6时，钢管柱轴压力增大变形能力减小，两类节点的滞回性能均受到明显影响，尤其是加腋节点在轴压比为0.8时滞回环数和包络面积急剧缩减。可见当轴压比较小时加劲腋板能增强节点的强度和变形能力，当轴压比较高时加劲腋板亦能增加节点的承载力但是节点变形能力相应降低。② 同一级循环荷载，加腋节点后续滞回环与首次循环滞回环的荷载值存在明显差距，节点存在明显强度退化，并且随轴压比越大强度退化越明显。对比分析图8(a)～(d)滞回曲线可知轴压比较小时普通节点强度退化不明显，随轴压比增加滞回环荷载峰值差距增大，强度退化越明显。③ 两类节点试件在初始加载阶段P–Δ曲线滞回环面积较小，荷载与位移之间呈直线变化，在节点往复过程中，残余变形亦极小，构件基本上处于弹性工作状态。但随荷载进一步增加，P–Δ曲线滞回环开始呈现曲线形，而且随往复荷载逐级增加节点的非弹性性能越来越明显，滞回曲线开始逐渐向位移轴倾斜而且普通节点的倾斜更严重，承载力开始逐渐下降，梁端的残余变形逐渐增加，并且每次卸载后残余变形的增加值大致相同。

图8 P－Δ滞回曲线Fig.8 P－Δ hysteretic curves

3.2 刚度退化曲线

往复荷载作用下，随循环荷载和控制位移Δ的幅值增加，塑性变形不断发展，刚度逐渐退化。本文采用同一级位移所对应的割线刚度来表示构件在低周往复荷载作用下刚度退化的特性。两类节点的刚度曲线如图9所示，对比分析可知:普通节点的初始刚度随轴压比增加而减小，当轴压比为0.2时，J－1的初始刚度为1330 kN·m，而当轴压比增加到0.8时，J－4初始刚度为1130 kN·m，减少了200 kN·m。但是当轴压比增加到0.8时，加腋节点的初始刚度从1580 kN·m增加到1740 kN·m，增加了160 kN·m。由此可见，加腋肋板提高了节点的初始刚度，防止了节点在荷载作用下产生过大的初始变形。

随循环荷载继续增加，两类节点的刚度均出现明显退化，控制位移越大，刚度退化越严重，轴压比越大刚度退化越快。并且由于包辛格效应，在同一循环荷载中，节点反向施载到相同控制位移Δ时其刚度明显小于第一次加载到相同控制位移Δ时的刚度。同时对比图9(a)与(b)也可看出相同往复荷载作用下加腋节点的刚度退化速度明显大于普通节点。

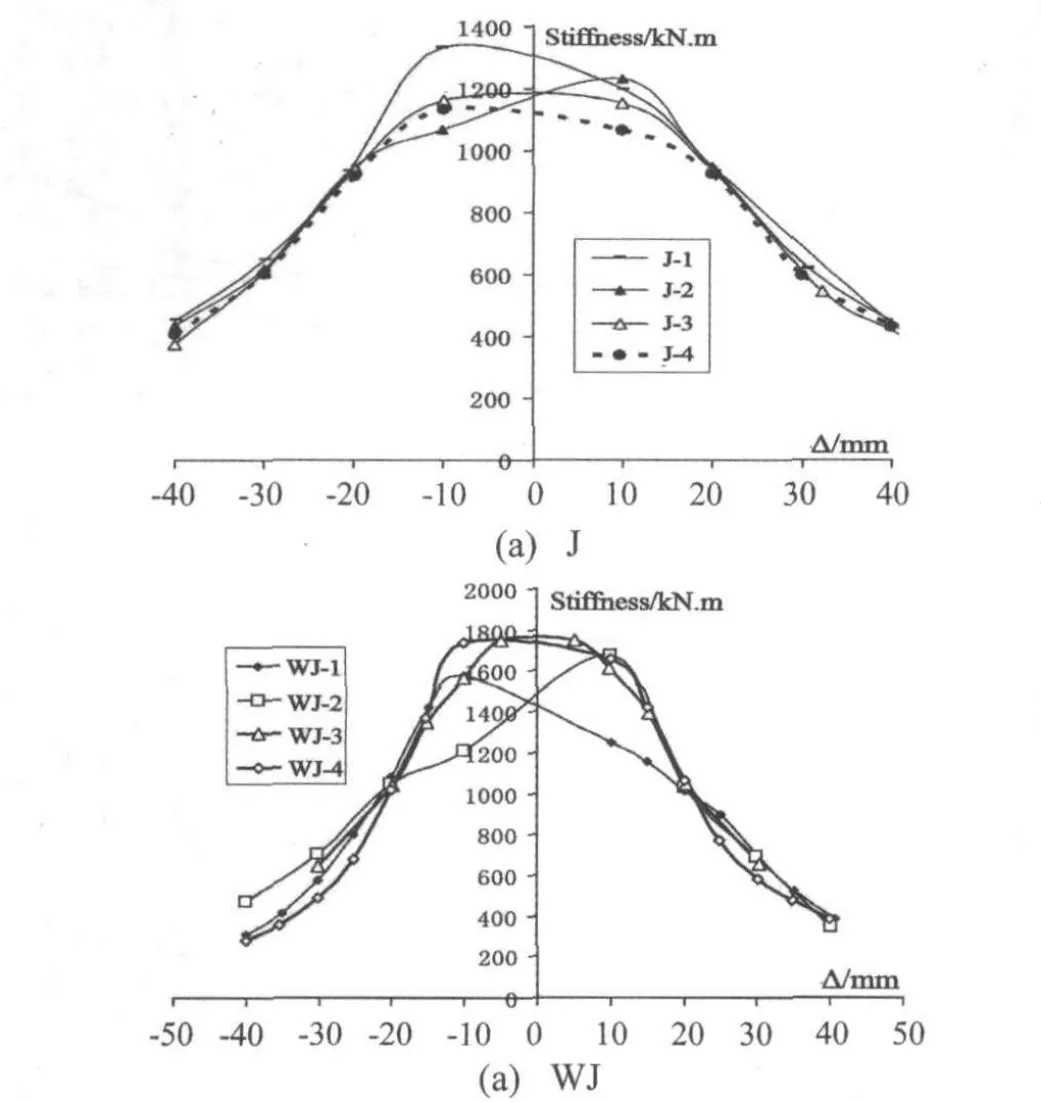
图9 刚度退化曲线Fig.9 Stiffness degenerated curves

3.3 延性及耗能性能

延性比是结构延性好坏的衡量标准，一般通过结构极限位移Δu与屈服位移Δy之比μ来表示。两类节点各试件的屈服位移、极限位移及延性系数如表2所示，不同轴压比下加腋节点梁与普通节点相比极限位移和屈服位移较大，延性系数高，抗震性能好。加劲腋板能增强节点区域的刚度使节点梁的弹塑性得到充分发挥，提高了节点的延性及往复变形次数。

结构耗能特性和阻尼是衡量结构抗震性能的重要指标，根据参考文献［10］的规定，计算可得衡量节点能量耗散能力的耗能系数E。实际应用中，等效粘滞阻尼比he亦是常用来衡量结构耗能能力的另一指标，等效粘滞阻尼比越大，结构的耗能能力越强。同时，在地震持续时间较长时，还需用累计能量消耗系数ηa来考虑节点累计耗能的能力。

两类节点耗能系数如表2所示，普通节点的耗能系数E和等效粘滞阻尼系数he受轴压比的影响小，随轴压比增加E和he减少了0.131和0.021，但累积耗能系数ηa却减少了2.45。与普通节点相比，轴压比对加腋节点耗能性能的影响更大，E、he和ηa随轴压比增加均有明显下降，分别减少了 0.487、0.076 和 10.56。由上述数据可知轴压比对加腋节点累积耗能性能影响最大，随轴压比增加加腋节点累积耗能能力急剧下降，但是试验中加腋节点累积耗能系数的最小值都大于普通节点的最大值。同时，由表2可得不同轴压比下普通节点的 E、he和 ηa的平均值分别为 1.18、0.19 和 8.45，而加腋节点的 E、he和 ηa的平均值则为 1.66、0.26 和15，可见加劲腋板提高了节点的强度、刚度以及各耗能系数，改善了节点的抗震性能。实际工程中，在抗震设防烈度高的地区，可考考虑采用加腋节点。

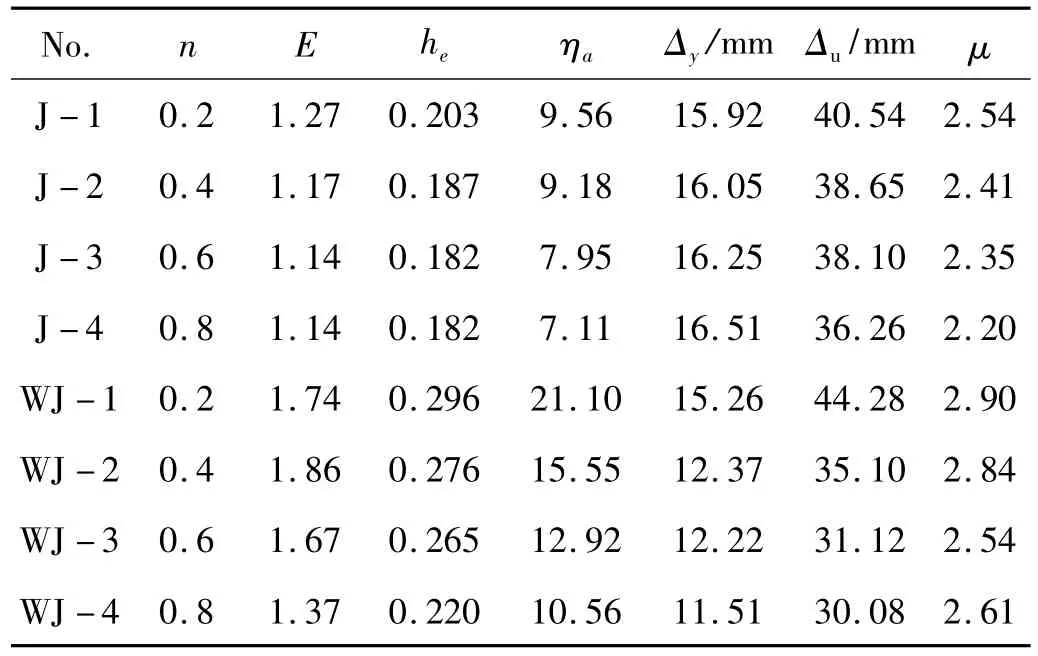
表2 延性比及耗能系数Tab.2 Energy dissipated capability and ductility coefficient

3.4 节点梁柱位移分析

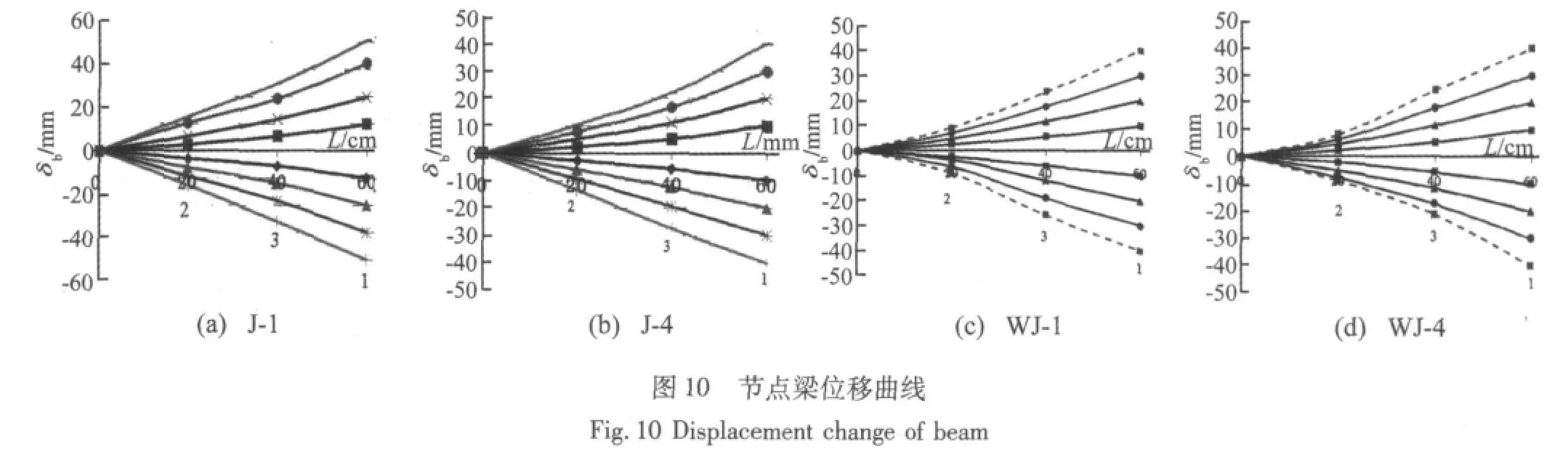
往复荷载作用下，通过对节点域周围梁柱位移的变化情况进行分析，可进一步了解节点的抗震性能。轴压比为0.2和0.8时两类节点梁的位移曲线(前几个荷载循环)如图10所示，往复荷载较小时，两类节点梁变形小，沿横梁长度L布置的位移计(1，2，3)测值δb连线为直线，未有明显曲率，节点产生转角位移。随往复荷载增加，位移计测值连线逐渐产生曲率，并随往复荷载增加而增大。此时，加腋节点钢管梁位移曲线在离节点20 cm处产生突变出现拐点，位移测值连线曲率增大，钢管梁在该区域出现了塑性铰，并且随轴压比增加钢管梁的弯曲程度增大。但整个往复加载过程中，不同轴压比下普通节点的钢管梁均未出现塑性铰，可见加腋节点达到了“强节点，弱杆件”的预期设计效果。同时，与普通节点相比轴压比对加腋节点横梁的位移幅值较小，不同轴压比下横向钢管梁均出现塑性铰。

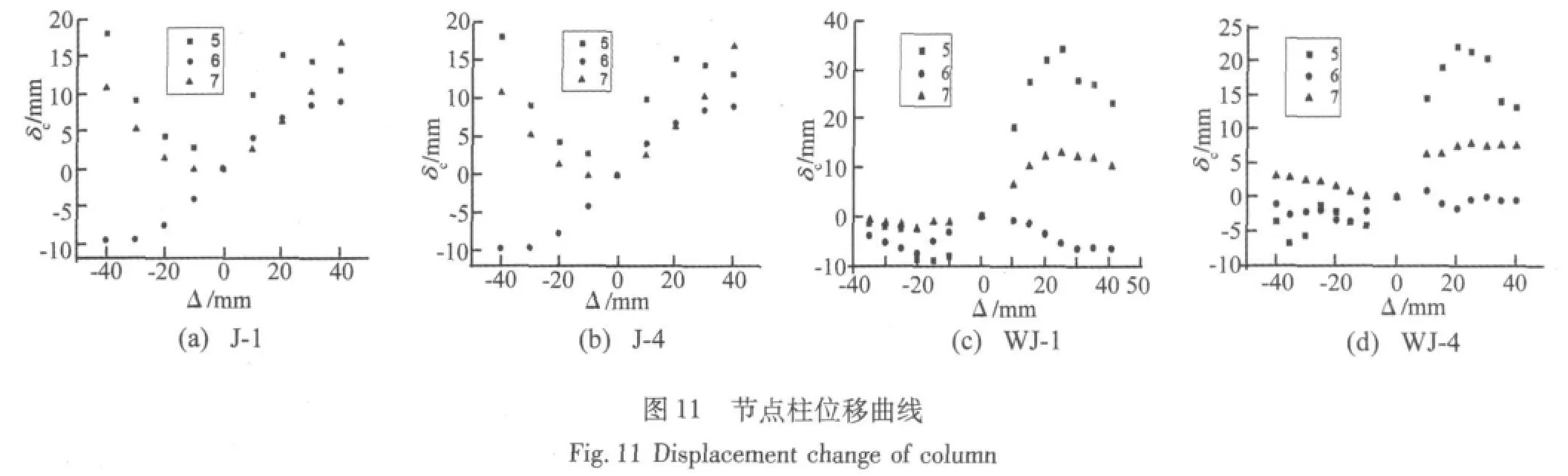
图11给出了轴压比为0.2和0.8时，前几个往复荷载循环中钢管柱在平面内(位移计6、7测值)与平面外(位移计5测值)侧移的变化情况。不同轴压比下，加腋节点钢管柱的平面外侧移随Δ增加而增大，并且侧移曲线具有明显曲率，约3mm达到最大值。而普通节点钢管柱的侧移则随Δ呈线性增加，约1.5mm达到最大值，然后柱平面外侧移因棱角开裂和正向循环荷载作用下钢管柱侧面受拉而逐渐下降。但是相同控制位移Δ处，两类节点钢管柱侧移均随轴压比增加而下降。负向循环荷载作用下，加腋节点平面外侧移相对较小。由此可见，加劲腋板提高了钢管柱自身变形的能力，循环荷载作用下钢管柱弹塑性性能得到发挥，但是普通节点试件因节点区域刚度和强度较弱自身变形较大，致使钢管柱直到节点破坏时还处于弹性变形阶段。普通节点柱平面内侧位与平面外侧移变化相同，而加腋节点的平面内侧移的变化相对复杂，但均小于平面外的侧移;而且随轴压比增加四个加腋节点试件的钢管柱平面内侧移逐渐减小，最大值分别为13.1mm、11.7mm、5.5mm、4.6mm。

4 有限元数值分析

4.1 单元模型

本文采用ANSYS软件对两类节点进行有限元分析，钢管采用三维各向同性8节点实体单元Solid95进行建模，柱上、下端采用固结约束。考虑材料非线性，采用多线性等向强化模型，使用多条直线段来模拟弹塑性材料的本构关系，材料遵守von Mises屈服准则及双线性随动强化(BKIN)准则。为真实反映试验与理论计算结果的偏差，在理论计算中模型参数均按表1设置，模型有限元网格划分如图12所示。

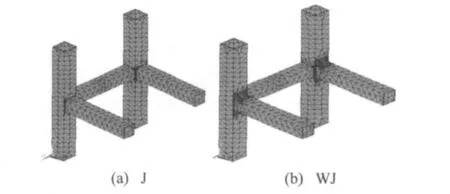
图12 焊接节点有限元模型Fig.12 Finite model of connections

4.2 结果对比

4.2.1 承载力

不同轴压比下，两类节点试件承载力的试验值和有限元数值计算值如表3所示，分析可知:① 随轴压比增加，两类节点屈服荷载Py的试验值PEy和计算值PFey均未出现明显变化，而且与普通节点相比加腋节点的屈服荷载值Py亦未得到明显提高。② 轴压比从0.2增加到0.8时，普通节点极限承载力的试验值PEu降低了1.68 kN，而加腋节点只降低了0.26 kN，但是两类节点极限承载力的有限元计算值PFEu却未出现明显变化。同时，计算可得不同轴压比下两类节点试件极限承载力的最大值和最小值仅变化8%。③ 不同轴压比下与普通节点相比加腋节点极限承载力的试验值和计算值均得到了明显提高。计算整理可得加腋节点与普通节点的承载力均值分别为20 kN和16 kN。由此可见，加腋节点及普通节点的屈服荷载和极限荷载均不随轴压比的增加而发生变化;虽然加劲腋板不能提高节点的屈服荷载，但是能够明显提高节点的极限荷载，改善节点的极限承载力。

同时，对比分析两类节点试验结果和有限元数值计算结果可知，因以下因素致使有限元数值计算结果均高于试验结果:① 试验中试件支座与有限元模型的边界条件存在差距。有限元计算时试件中钢管柱的上下支座均假设为理想固结，但实际试验加载过程中钢管柱的弯曲变形等致使柱上下端板均产生了转动变形，表现出一定程度的铰接性质。② 有限元数值计算中本构模型较为理想，与试验模型存在一定的误差。③ 文中节点试件为三维空间节点模型，梁柱构件较多，焊缝增加，提高了控制焊接质量的难度，而有限元数值计算中则不存在此问题。④ 其他试验误差等因素的影响致使试验值较有限元数值计算值减小。上述各因素致使试验和计算结果未能十分精确地相吻合，但是与试验结果相比计算结果的最大偏差亦未超过15%。

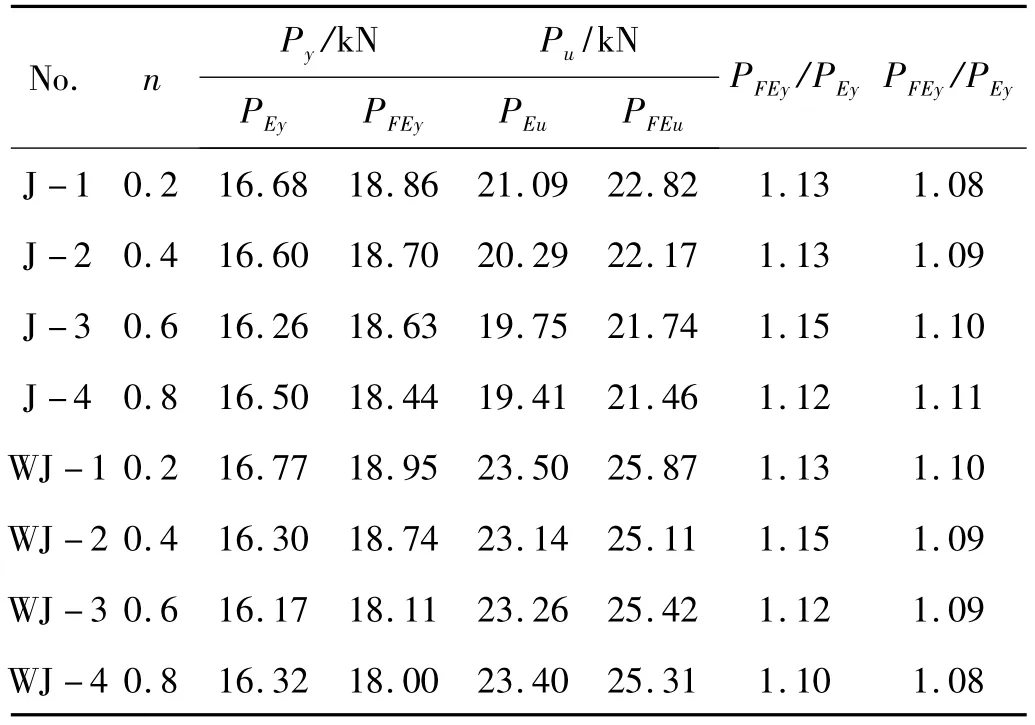
表3 节点承载力对比分析Tab.3 Comparison of experimental and simulated results

4.2.2 骨架曲线

本次分析取第一循环峰值点连接组成的包络线作为骨架曲线，普通节点试件的骨架曲线如图13所示。图13(a)与图13(b)中骨架曲线形状相同，各试件试验和有限元数值计算的荷载值P相差较小，并且随Δ的变化趋势相似。开始加载阶段两类骨架曲线均出现直线段，荷载P呈线性增加，试件处于弹性阶段;随循环荷载增加节点进入弹塑性变形，并达到极限承载力，随后节点进入塑性变形，承载力逐渐下降。图14给出了加腋节点的骨架曲线，图14(b)中有限元数值计算的骨架曲线较真实地模拟出了图14(a)中试验骨架曲线的发展趋势，试验中不同轴压比下各加腋节点试件的塑性变形和承载力下段均得到了真实的反映。

同时，由图13可见控制位移在－5mm～5mm之间普通节点的骨架曲线基本为一直线并且曲线间间距小，比较接近，表明在弹性变形阶段轴压比对节点的承载力影响较小;而由图14可知加腋节点在控制位移－15mm～15mm之间的骨架曲线均为直线，可见加劲腋板亦可提高梁柱节点的弹性变形能力。② 随往复荷载增加，节点达到极限承载力，而且各节点极限承载力随轴压比增加有较小的下降。这与4.2.1关于两类节点承载力的分析是一致的。③ 达到极限荷载后，各节点试件的承载力随即进入下降阶段。由图14可知加腋节点承载力下降阶段较普通节点明显，而且下载阶段相对较长，节点存在良好的塑性变形。并且在同一往复荷载循环中，正向循环时加腋节点的承载力均大于负向循环时所得的承载力，表出明显的包辛格效应。

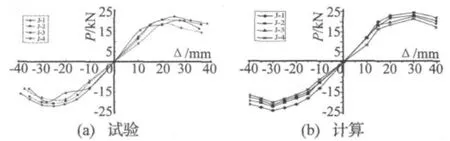
图13 J节点P－Δ骨架曲线Fig.13 P－Δ skeleton curves of J

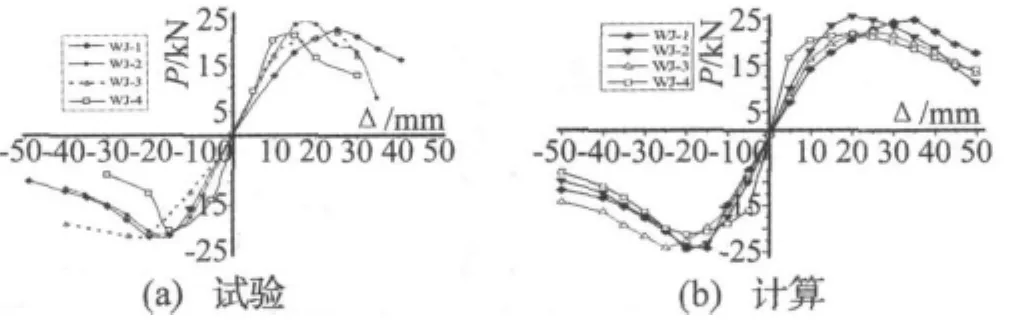
图14 WJ节点P－Δ骨架曲线Fig.14 P－Δ skeleton curves of WJ

5 结论

本文对普通节点和加腋节点的抗震性能进行了试验研究，基于试验结果及有限元数值计算分析得到了以下结论:

(1)相同轴压比下加腋节点与普通节点试件的最终破坏模式不同。普通节点最终破坏均是由钢管柱棱角开裂或梁柱连接焊缝拉裂引起，而加腋节点则是因钢管梁塑性变形过大出现局部屈曲导致节点失效。

(2)轴压比对节点的滞回性能影响较大。随轴压比增加节点塑性变形能力降低，脆性破坏特征逐渐增加，滞回环和包络面积急剧减小，耗能能力降低。

(3)加劲腋板能显著提高节点的极限荷载，改善节点的极限承载力。试验中加腋节点与普通节点的承载力均值分别为20 kN和16 kN，与普通节点相比加腋节点承载力可提高25%左右。

(4)加劲腋板提高了节点的延性系数和往复变形次数，增大了节点的粘滞阻尼和耗能性性能，尤其对节点的累积耗能能力得到了显著的提高，延长了节点塑性变形时间，从而改善了节点的抗震性能。

［1］GB 50018－2002冷弯薄壁型钢结构技术规范［S］.北京:中国计划出版社，2003.(GB 50018 －2002.Technical Code for design of cold-formed thin-wall steel structures［S］Beijing:China Planning Press，2003(in Chinese)).

［2］Zarghamee M S，Ojdrovic R P.Northridge postscript:lessons on steel connections［M］.Civil Engineering，1995.

［3］Nakashina M，Inoue K，Tada M.Classification of damage to steelbuildingsobserved in the1995 Hyogoken-Nanbu earthquake［J］.Engineering Structures，1998，20(4 －6):271－281.

［4］Zardhamee M S，Ojdrovic R P.Northridge postscript:lessons on steel connections［J］.Civil Engineering，ASCE，1995，65(4):68－71.

［5］SAC Joint Venture.Interim guidelines:Evaluation，repair，modification and design ofwelded steelmomentframe structures［R］.FEMA 267，SAC－95－02，1995.

［6］Uang C M，Bondad D，Lee C H.Cyclic performance of haunch repaired steel moment connections:experimental testing and analytical modeling［J］.Engineering Structures，1998，20(4－6):552－561.

［7］Uang C M，Yu Q S，Gross J.Cyclic testing of steel moment rehabilitated with RBS or welded haunch［J］.Journal of Structural Engineering，ASCE，200，126(1):57－68.

［8］Yu Q S，Uang C M，Gross J.Seismic rehabilitation design of steel moment connection with welded haunch［J］.Journal ofStructural Engineering，ASCE，200，126(1):69－78.

［9］Lee C H，Jung J H，Oh M H，et al.Cyclic seismic testing of steel moment connections reinforced with welded straight haunch ［J］.Engineering Structures，2003，25:1743－1753.

［10］GB 50011－2001建筑抗震设计规范［S］.北京:中国建筑工业出版社，2001.(GB 50011－2001 Code for seismic design of buildings［S］.Beijing:Chinese Building Industry Press，2001 (in Chinese)).

［11］GB 6397－86金属拉伸试验试样［S］.北京:中国建筑工业出版社，1986.(GB 6397－86 Metallic materials-test pieces for tensile testing［S］.Beijing:Chinese Building Industry Press，1986(in Chinese)).

［12］JGJ 101－96建筑抗震试验方法规程［S］.北京:中国建筑工业出版社，1997.(JGJ 101－96 Specification of testing methods for earthquake resistant building［S］.Beijing:Chinese Building Industry Press，1997(in Chinese)).

［13］GB/T 2975－1998钢及钢产品力学性能试验取样位置及试样制备［S］.北京:中国建筑工业出版社，1998.(GB/T 2975－1998 Steel and steel products-location and preparation of test pieces for mechanical testing ［S］.Beijing:Chinese Building Industry Press，1998(in Chinese)).