接触问题的MPI+OpenMP混合并行计算

肖永浩，莫则尧

(1.中国工程物理研究院 计算机应用研究所，四川 绵阳 621900;2北京应用物理与计算数学研究所，北京 100088)

接触问题广泛存在于汽车碰撞，金属成型等工程应用和现实生活中，对接触问题的数值模拟对于安全问题、武器模拟等非常重要。作为非线性大变形问题，接触问题的并行计算受到广泛关注。国外接触问题及其并行算法已有多年研究，PRONTO3D［1］，ALE3D［2］等程序都可进行接触问题的大规模并行计算，其并行算法值得借鉴。国内主要依赖DYNA、ABAQUS等商业软件，寇哲君［3］，亓文果［4］等在集群环境下进行了汽车碰撞的小规模并行模拟。

并行程序运行于并行机上，并行机的体系结构直接影响并行程序的性能。当前，节点内部多处理器共享内存而节点间分布式内存的多处理器集群(CLUsters of MultiProcessors，CLUMPs)成为主流。在多处理器集群存在两种编程模式，称之为单一编程模式和混合编程模式［5］。单一编程模式采用单一的API描述多处理器节点间和节点内部的通信，由于并行计算主要通过处理器间的消息传递(如 Message Passing Interface，MPI)来完成，因此这种模式也称为消息传递模式。混合编程模式将节点内的共享存储模式与节点间的消息传递结合起来。单一编程模式可采用MPI实现，混合编程模式可采用MPI+OpenMP实现。

虽然在大部分情形下，基于MPI实现的单一模式的并行程序的性能要优于混合并行模式的程序［5］，但是在诸如全局通信量很大，内存受限等条件下，混合并行模式的程序在CLUMPs系统上的性能要好于单一模式的程序。本文在接触计算程序IPDC的基础上，根据接触计算的特点，采用混合编程模式实现了接触问题的并行计算。

1 接触问题

接触计算一般采用Lagrangian有限元方法，其基本方程通过有限元离散后写成矩阵形式为:

时间方向采用显式时间积分，即对式(1)，若已知第n步的节点力，第n+1步的节点位移可以用下式计算:

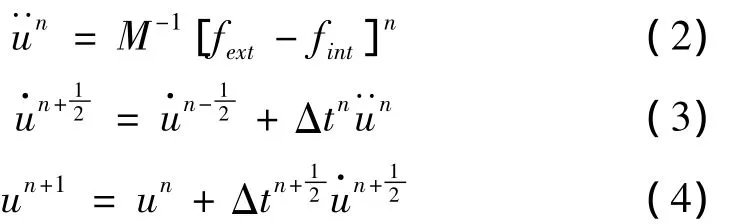
在一个时间步内，计算过程分为内力计算和接触力计算。其中内力计算通过计算单元应变率，应用本构方程计算单元应力，最终通过对单元节点的力装配得到节点内力。接触力计算用于更新接触点的接触力，其计算过程分为全局搜索，局部搜索和接触力更新，全局搜索确定离接触面片最近的接触点，局部搜索确定接触点在接触面片上具体的穿透点，最后更新接触力。接触问题的计算流程如图1所示。

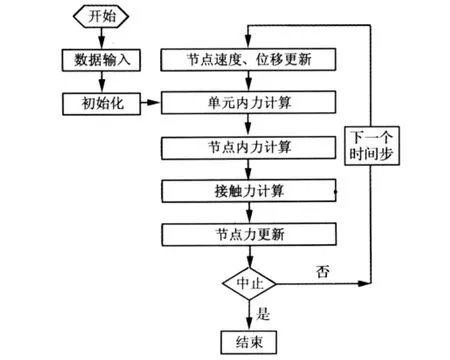
图1 接触计算流程Fig.1 Outline of contact problem solving

接触力计算中全局搜索是最耗时部分，point-in-box(捕捉盒)［1］、bucket-sorting(桶排序)［6］等算法用于加速接触点之间临近关系的搜索，其原理都是通过对搜索空间的划分，减少全局搜索量，本文程序采用桶排序算法。而接触力更新算法有罚函数法，动态约束法，分布参数法等［7］，本文程序采用罚函数法，即根据接触点穿透接触面片的穿透深度确定接触点所受到的接触力。

2 双重区域剖分算法

根据接触问题算法，时间步之间是严格顺序依赖关系，并行计算只能在时间步内进行。在一个时间步内，内力计算和接触力计算的计算对象是不同的，内力计算针对的是模型中所有的有限元网格，包括单元和节点，而接触力计算只针对模型外表面的面片和构成面片的节点。并且内力计算和接触力计算的对象间数据依赖性质不同，内力计算中数据依赖基于有限元网格拓扑连接，而接触力计算基于接触点的空间邻近关系。为了达到两部分计算的负载平衡，两部分的并行计算采取两种区域剖分算法，称之为双重区域剖分算法。

在碰撞计算过程中单元拓扑连接关系不变，因此内力计算区域只需要剖分一次，达到静态负载平衡即可。但是接触力计算中接触点之间的空间临近关系是时变的，易引起负载的动态不平衡。双重区域剖分算法不仅能较好的处理两种计算区域不同性质的剖分问题，而且可以通过对接触力计算区域的动态重剖分实现动态负载平衡。

接触问题的双重区域剖分算法步骤如下:

(1)内力计算区域剖分。

(2)内力 fint并行计算。

(3)接触力计算区域剖分。

(4)接触力并行计算。

(5)节点力更新，即计算f=fext－ fint。

(6)节点加速度、速度、位移更新，转至第(2)步。

2.1 内力并行算法

内力并行计算是直接的，在一个显式时间步中，每个单元只和其有限元网格拓扑关系上相邻单元有关系。每个内力计算子区域只需和这个子区域边界单元相邻单元所在的子域进行通信。

具体的，在每个时间步，单元应力、应变等的计算只需组成本单元节点的速度，位移等信息，可以并行更新。节点内力是由所有与这个节点相连接的单元应力装配得到的，因此，子区域间共享节点的节点内力装配需要拥有这个节点所有子区域得到的节点内力相加得到。

2.2 接触力并行算法

接触力计算中，局部搜索和接触力更新是局部计算，并行算法的核心是并行全局搜索算法，本文采用基于并行桶排序算法的全局搜索算法。假设已有分布于多个处理器上的内力计算子区域，而接触点是分布在各个内力计算子区域中的，接触力并行计算流程如下:

(1)根据内力计算子区域中接触点坐标构造全局桶。

(2)基于全局桶进行区域剖分，得到接触力计算子区域。

(3)内力计算子区域确定接触点所属接触力计算子区域，得到内力计算子区域和接触力计算子区域间通信关系。

(4)内力计算子区域发送接触点信息到接触力计算子区域。

(5)局部搜索和接触力更新。

(6)接触力计算子区域发送接触力至内力计算子区域。

3 并行实现

3.1 MPI实现

内力计算的区域剖分采用图剖分(Metis)实现，即将网格抽象为图，图的顶点代表单元，图的边代表单元间存在公共面，基于不同材料而导致单元计算量的不同，可通过施加图中顶点的权值来达到负载平衡。

接触力计算时，接触点空间坐标的时变导致接触点间空间临近关系未知，因此接触力计算的区域剖分面向并行桶排序。得到全局桶后，将每个桶抽象为图的顶点，若两个桶相邻，则相应的顶点间存在一条边，由此得到的图是接触点间临近关系图的一个超图。每个桶中接触点的数目作为相应顶点的权重，用于表示计算负载，最后通过图剖分(Metis)实现接触力计算区域的剖分。

接触点空间坐标的时变性质会导致接触力并行计算时负载的动态不平衡现象，为了实现负载平衡，需要进行接触力计算区域的重剖分。但是从接触力并行算法可知，其区域剖分需要耗时的全局操作，为了减少这种区域重剖分的次数，在确定内力计算区域和接触力计算区域通信关系时考虑发送冗余信息，内力计算子区域将接触力计算子区域中每个面片相邻的多个接触点发送给接触力计算子区域，使得在若干个时间步内，接触力计算子区域中的面片能在本区域找到最近的接触点。

并行程序中消息传递采用MPI实现，基于MPI的并行程序可运行在分布式内存和共享内存并行机上。

3.2 OpenMP实现

OpenMP是科学计算领域中共享内存并行机的主要并行化范式，运行在共享内存节点上的OpenMP程序在内存需求、编程效率等各方面都有它的优点［8］。OpenMP并行化最简单的方式是针对程序中的循环采用指导语句$OMP PARALLEL DO并行化。由于OpenMP指令本身带来的同步等系统开销，并行化所有的循环并不是最好的选择，可采用基于性能检测的增量并行模式，其流程见图2。这种方法通过测试典型算例来确定哪些循环需要被并行化，能保证所有并行化都能减少总的执行时间。

除了采用增量并行化方法外，增加OpenMP并行的粒度，是提高程序并行效率的另外一个途径。本文采用分块数据结构对单元进行分块操作。通过将循环中间计算数据的成块缓存，不仅能充分利用计算机的Cache，而且能增加 OpenMP 并行粒度［9］。

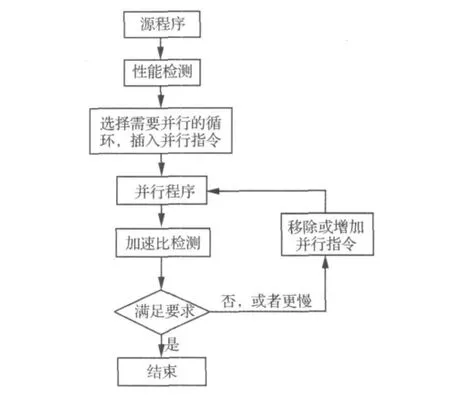
图2 OpenMP中增量并行模式Fig.2 Incremental parallelization model with OpenMP

以具体程序为例，假设要对NUM_ELE个单元进行计算，原始程序表示为:

假设单元块大小为NBLOCK，假设单元分为NUM_ELE_BLOCK块，有 NUM_ELE_BLOCK=NUM_ELE/NBLOCK。基于分块数据结构的单元块计算为BLOCK_OPERATION，经过分块和OpenMP并行化后的程序表示为:

采用顺序分块时，即根据通过对单元顺序遍历，将每NBLOCK个单元为一块。BLOCK_OPERATION(J)有如下形式:

分块数据结构提供了数据遍历的另一种方法，可以根据OPERATION中操作的数据对象确定分块方法，以增加每次OPERATION中从内存中读取和存储的数据的局部性，从而提高程序效率。本文程序采用顺序分块，今后将对其他分块方式进行研究测试。分块大小NBLOCK是可变的，其大小会影响程序运行效率，具体计算时可根据实际计算机环境和具体算例测试进行调整。

3.3 MPI+OpenMP 实现

基于双重区域剖分的接触并行算法在接触力计算和内力计算子区域之间的通信是全局通信，随着处理器数的增多，全局通信的开销增加的速度会远远大于通过并行计算而减小的计算开销，通过MPI+OpenMP混合并行模式的计算可有效的减少MPI中的全局通信开销。

MPI+OpenMP混合并行模式在每个MPI进程计算时增加OpenMP线程。MPI可以在CLUMPs节点间和节点内部实现信息传递，而OpenMP在节点内部利用共享内存实现并行计算。OpenMP可使用最大线程数为节点内部共享内存的处理器(核)数。通过程序输入参数调整，程序可以为串行程序，MPI并行程序，OpenMP并行程序，和MPI+OpenMP并行程序，使用何种并行模式取决于可用硬件资源，问题规模和并行程序特性。图3给出了接触并行计算中MPI+OpenMP混合并行计算模式，图中是在节点内部采用2个OpenMP线程对内力计算部分并行实现。

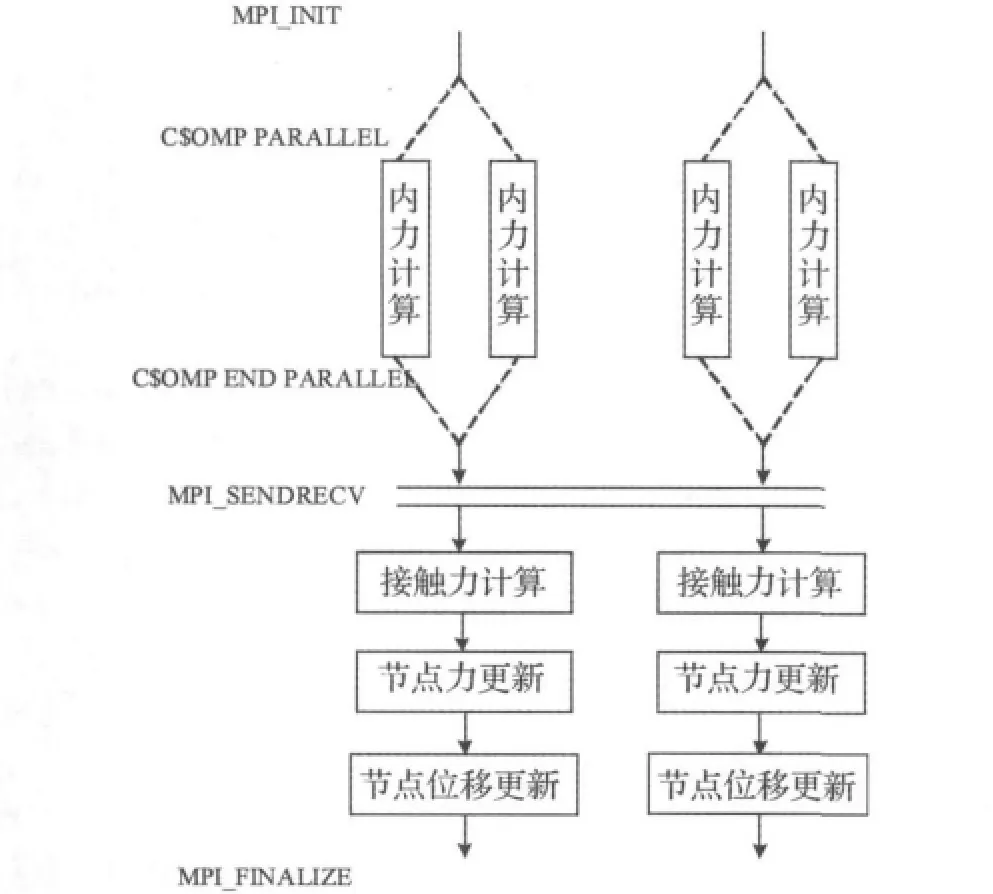
图3 接触并行计算中MPI+OpenMP混合并行计算模式Fig.3 MPI+OpenMP hybrid model in contact parallel computing

4 数值模拟实验

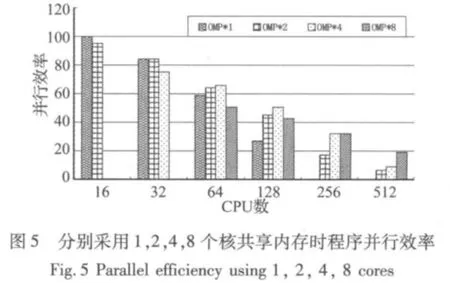
在某国产大型机上对接触并行程序进行了数值模拟测试实验。实验平台计算节点由8个处理器核共享32G内存。模拟锥形桶撞击平板过程，模型采用8节点实体单元，模拟自由度为1千万，计算5000时间步。图4给出了计算模型。测试时每个计算节点内部可使用1～8个处理器核共享内存并行，即OpenMP并行最多可使用8个处理器核，程序中分块大小取128。图5给出了从总处理器核数为P=16～512时，分别采用OMP=1，2，4，8个核共享内存时的程序并行效率，若记MPI进程数为MPIP，有P=OMP*MPIP。

从图5可知，在总处理器核数较少时，采用单一模式的MPI程序(OMP=1)的性能好于混合模式的性能。随着总处理器核数的增多，采用适当的OpenMP共享内存并行将提升并行效率。总处理器核越多，为了达到较好的并行效率，每个节点采用共享内存的核数需要越多，至总处理器核数512时，每个节点采用8个核共享内存时并行效率最好，此时有64个MPI进程参与并行计算。

为了深入分析产生以上现象的原因，给出总处理器核数为32，128，512，采用 OpenMP 线程数为 1，2，4，8时，总计算时间，内力计算时间和全局通信时间的趋势图，见图6。从图中可以看出:① 总处理器核数一定的情形下，全局通信时间随着OpenMP线程数的增加而下降。原因是MPI进程数随着OpenMP线程数的增加而减少。② 总处理器核数一定的情形下，内力计算部分开销随着线程数增加而增加。原因是内力并行计算部分通信简单，基于MPI的并行效率要高于基于OpenMP的并行效率。在总处理器核数为512时，采用4个线程的计算时间要小于采用MPI并行的时间，其原因可能是由于此时并行粒度较小，OpenMP并行效率在粒度较小时占优，但是随着线程数的继续增加，OpenMP系统开销增加较多，其运行时间又多于MPI并行程序。③ 随着总处理器核数的增多，全局通信在总计算时间中占有比例增加。如32处理器核时内力计算时间大于全局通信时间，而128处理器核时两条线有交叉，至512处理器核时全局通信时间大于内力计算时间。④总计算时间随着OpenMP线程增加的趋势从左至右依次为单调增加，先下降再增加，单调下降。

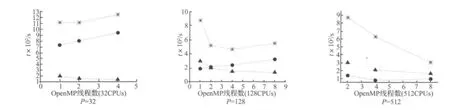
图6 不同处理器规模下的总计算时间(﹡线)，内力计算时间(●线)和全局通信时间(▲线)Fig.6 Total time(line with﹡)，Computing time of internal force(line with●)，and communication time(line with▲)with different CPUs

接触问题性质是产生以上现象的主要原因。内力计算子区域和接触力计算子区域间需要较多的通信，而且接触力计算区域剖分过程中需要全局通信，全局通信在分布式并行机上会严重影响并行效率，随着参与全局通信的处理器核数的增多，其影响越大。也就是说接触力并行计算中采用的处理器核数越多，全局通信的负面影响将越大。

位于每个节点内部的OpenMP并行模式下的并行程序可扩展性有限。原因之一是OpenMP并行只能针对部分程序并行化，其并行效率受限于串行运行部分;另一个原因是采用较多处理器核时OpenMP并行程序的系统开销，如隐式同步，Cache一致性等开销较大，降低了并行程序的效率。在本文算例中，通过增加OpenMP线程得到的内力计算部分并行效率在8核时只有50%～55%。在总处理器核数较少的情形下，OpenMP的并行效率低于MPI并行程序效率。

随着接触力并行计算采用的处理器核越多，由接触力计算部分产生的全局通信的开销会增加，最终通信开销的增加会抵消由处理器核数增加带来的计算时间好处。而在总处理器核较多时，采用OpenMP并行程序能通过内力计算部分的并行计算减少内力计算部分的运行时间，但接触力计算中全局通信量并没有增加。

5 结论

针对接触计算特点，在设计双重区域剖分并行算法的基础上，采用MPI+OpenMP的混合编程模式实现了接触问题的并行计算。采用基于分块的数据结构增加了OpenMP的并行粒度，OpenMP并行实现可有效的减少MPI并行程序在处理器核数较多时接触力并行计算中的全局通信开销。数值实验表明该并行程序能在数百处理器上计算上千万自由度的接触问题，而且具有较好的并行效率。今后将针对算法特点进行进一步的优化。

［1］Attaway S W，Hendrickson B A，Plimpton S J，et al.A parallel contact detection algorithm for transient solid dynamics simulations using PRONTO3D［J］.Computational Mechanics，1998，22(4):143 －159.

［2］Pierce T，Rodrigue G.A parallel two-sided contact algorithm in ALE3D［J］.Computer Methods in Applied Mechanics and Engineering，2005，194(27 －29):3127 －3146.

［3］寇哲君，程建刚，姚振汉.机群环境下汽车碰撞的并行模拟［J］.清华大学学报(自然科学版)，2003，43(5):666－668.

［4］亓文果，金先龙，张晓云.冲击－接触问题有限元仿真的并行计算［J］.振动与冲击，2006，25(4):68－72.

［5］Cappello F，Etiemble D.MPI versus MPI+OpenMP on IBM SP for the NAS Benchmarks.Supercomputing，ACM/IEEE，2000 Conference［C］.Dallas，04 －10 Nov，2000.

［6］Har J，Fulton R E.A parallel finite element procedure for contact-impact problems［J］.Engineering with Computers，2003，19(2):67－84.

［7］白金泽.LS－DYNA3D理论基础与实例分析［M］.北京:科学出版社，2005.

［8］Bader D A，都志辉译，面向千万亿次计算的算法与应用［M］.北京:清华大学出版社，2008.

［9］肖永浩，黄清南.基于分块数据结构的冲击问题并行计算［J］.计算机辅助工程，2011，20(1):33 －36.