基于混沌理论的心音信号非线性动力学分析

丁晓蓉，郭兴明，钟丽莎

(重庆大学 生物工程学院，重庆 400044)

心音是心动周期中心肌收缩、瓣膜开闭、血液流动等因素引起的机械振动所产生的声音，它是心脏机械活动的直接反映。当心血管疾病尚未发展到足以产生某种病变以前，心音中就会出现关于心脏各个部分如心房、心室、大血管、心血管及各个瓣膜功能状态的重要病理信息，对心脏疾病的诊断具有重要的意义。近年来国内外学者［1－2］对心音信号的研究提出了大量的分析识别算法并取得了一些成果，然而这些研究多是构建在心音信号线性(时变或时不变)模型基础之上的，即将产生心音信号的心脏动力学系统进行简化和抽象，建立理想的线性模型(如ARMA模型)。而心脏本身是一个由多种因素控制的复杂非线性系统，如果仅对其进行线性近似及相应的分析，就不可能从本质上认识生命活动规律，尤其是与非线性相关的特征规律［3－5］。国内外有学者［6－9］对心音信号进行探索性地研究，得出了一些有价值的信息。而目前临床上已有很多对二尖瓣狭窄进行诊断的方法，如右心导管术、超声心动图等。席晓萍［10］分别用超声心动图和心电图对二尖瓣左房扩大进行了研究，发现超声心动图与心电图对左心房扩大的检出率有显著性差异，二者对二尖瓣的临床诊断都有重要的意义。刘兵等［11］采用超声及可视化心音图对二尖瓣狭窄心杂音信号进行分析，得出了三维可视化心音图在二尖瓣狭窄临床诊断中的价值。当二尖瓣本身并未发生器质性病变，而由于经二尖瓣口的流量增大、流速增快以及主闭返流入左室的血液冲击二尖瓣前叶等因素，会发生相对性或功能性二尖瓣狭窄，此时心音会出现异常，例如舒张期杂音，从而有利于对二尖瓣狭窄进行早期诊断。同时由于二尖瓣狭窄而导致的血液动力学等方面的改变会导致相应的心音信号的复杂度及平稳性发生变化，而从非线性混沌的角度能够较好地反映这些变化，揭示与正常心音之间存在的差异性。

本文拟从混沌理论的角度对心音信号进行分析，作为非线性系统的一种极为重要的运动形态，混沌是指确定性系统中出现的具有随机性的运动，它揭示了非线性系统中有序与无序的统一，确定性与随机性的统一。将有助于我们更好地理解人体生命过程的非规则的动力学特性，并且用非线性的方法对心脏的健康和病理状态进行研究更能反映心脏的功能状态。

1 混沌特征提取算法

1.1 相空间重构

混沌分析所要进行的第一步工作是要对混沌信号进行相空间重构以恢复混沌吸引子，后者作为混沌系统的特征之一，体现着混沌系统的规律性——混沌系统最终会落入某一特定轨迹之中，这种特定的轨道就是混沌吸引子［12］。

混沌时间序列的相空间重构普遍采用Packard［13］提出的坐标延迟的相空间重构方法［14］，其本质是通过一维时间序列{x(n)}的不同时间延迟来构造m维相空间矢量:

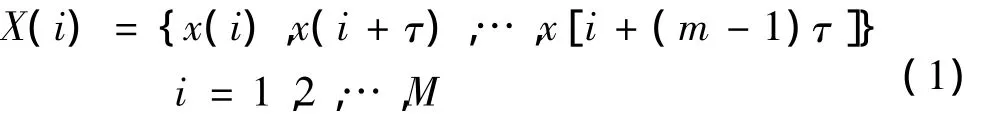
其中:M=N－(m－1)τ为矢量总数，m为嵌入维，τ为时间延迟，m和τ是坐标延迟相空间重构技术的两个关键参数。适当的时间延迟可以消除时间序列的自相关且使系统保持非线性结构;而对于嵌入维数m，当其满足Takens嵌入定理m≥2d+1(d为混沌吸引子的维数)时，重构后的相空间能够体现原系统的特性，所以只需确定反映结构的最小m值即可，太大的嵌入维数会造成数据的浪费，而太小的嵌入维数又不利于反映真实系统的结构。

τ的确定有自相关法、平均位移法和复自相关法等方法，但由于不满足非线性以及计算性能方面的缺陷，这些方法一般不用于计算τ，相比之下互信息法更具优点。Fraser等［15］提出用互信息来判断系统的非线性相关性，由于互信息量I(τ)的极小值表示x(t)和x(t+τ)是最大可能的不相关，所以重构时使用I(τ)的第一个极小值作为最优延迟时间。最小嵌入维数采用Cao［16］提出的最小邻近点改进算法——Cao法，计算时只需要延迟时间τ一个参数，就能够有效区分随机信号和确定性信号，并且使用较小的数据量就可以求得嵌入维。根据Cao算法，如果时间序列是确定的，则嵌入维是存在的，E1(m)将在m大于某一特定值m0后将不再变化。若时间序列是随机信号，则E1(m)应逐渐增加，但在实际应用中对一有限长序列E1(m)究竟是在缓慢变化还是已经稳定不容易判断，因此补充一个判定随机序列的准则。对于随机序列，数据间没有相关性，即不具备可预测性，E2(m)将始终为1;对于确定序列，数据点之间的相关关系式依赖于嵌入维m值变化的，总存在一些m值使得E2(m)不等于1。

1.2 关联维数及其计算方法

混沌理论中的分形维数是定量刻画混沌吸引子的一个重要参数，广泛应用于非线性行为的定量描述中。关联维数为分形维数的一种，最初由Grassberger和Procaccia［17］提出。计算关联维数的算法称为 G-P算法，被广泛地应用于维数分析中，可以用于生理信号特征的提取中，能有效地诊断心音信号［7］。

对于重构后的心音相空间，关联维数D可以通过计算关联积分Cm(r)获得，它是m维相空间中点对(Xi，Xj)之间距离小于超球体半径r的点对占相空间中所有点对(总点对数为M(M－1))的比例，其计算公式为:

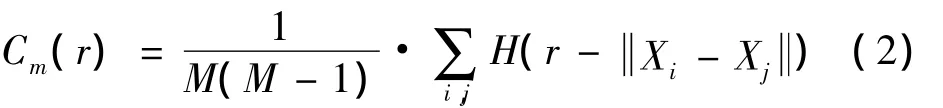
其中:M=N－(m－1)τ为相空间总点数，H是Heaviside函数，满足:

对于适当选取的 r，在无标度区存在如下关系:Cm(r)≈rD(m)，可以推导出即为关联维数。

1.3 最大Lyapunov指数的计算

Lyapunov指数是定量描述混沌系统的重要指标，它反映了相空间内系统相邻轨道收敛和发散的长期平均水平。Lyapunov指数是检验系统不稳定、出现混沌的一个非常有用的特征量，系统Lyapunov指数为正即意味着混沌，并且指数越大，说明混沌特性越明显，混沌程度越高。本文采用改进的最大Lyapunov指数算法计算Lyapunov指数。它通过τ和m重构相空间后，对重构的轨道X中的每一点Xi寻找其最近的邻域，这种最近邻域Xi间必须有短暂的分离，以保证邻域点对沿着不同的轨道运动。用FFT来计算序列的平均周期T，并取分离间隔为w=T/Δt为序列的采样周期。假定di(0)为到第i个点最近邻域的距离，即:

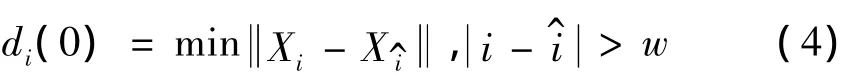
对相空间中的每个点Xi，计算出该邻近点对在j个离散时间步后的距离:

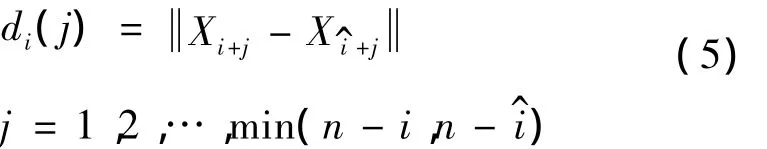
假定第i个最邻近点近似以最大Lyapunov指数的速率指数分散，即 di(j)=，此处 Ci为初始的分离距离常数。对其两边取对数，得:

方程代表一簇近似平行线，斜率为λ1。可以用最小二乘法拟合得最大Lyapunov指数λ1:

1.4 递归图及其定量分析

由于构成混沌吸引子的非稳态轨道在有限的的吸引子空间中会不断地近似逼近及分叉远离，从而出现递归现象。将系统中提取的时间序列重现系统动力学递归行为的方法即为递归法［18］。根据上述相空间重构方法，得到相空间矢量 Xi，i=1，2，…，M，其作为行和列构成N×N的矩阵递归图，图中的每个点由对应的行、列向量点之间的距离来描述:

式中:ε为临界距离，是预先确定的阈值，θ(x)是Heaviside 函数。当 Ri，j为 1 时，在递归图中(i，j)位置上表示为一个黑点，而当其为0时，(i，j)位置上表示为一个白点。所以，递归图将一个m维相空间的轨迹映射到一个二维图上。RP图可用于信号的定性分析。通过分析信号的递归图，可以直观地知道信号的复杂度，如周期性、平稳性、可预测性。为了量化递归图中的系统递归现象，Zbilut等［19］提出了定量递归分析，通过递归度(%REC)、确定性(%DET)、比率(Ratio，%DET 与%REC的比值)、线段分布熵(ENT)等量化参数来描述系统的动力学行为。其中，%REC表明了d维相空间中彼此靠近点额嵌入矢量的比例，较大的%REC意味着较长的周期性嵌入过程;%DET描述的是轨道周期递归的程度，值越大表明确定性却强，反之随机性越强;而ENT则代表动力学信息量或随机性的程度，用来说明递归图的复杂性。

2 心音信号分析

首先，采用心音采集设备采集健康及病理心音信号;然后，对心音信号进行去噪处理;最后，通过上述介绍的混沌算法对心音信号进行处理，包括计算关联维数、最大Lyapunov指数，及获取递归图和相应的定量分析。

2.1 心音信号的采集及预处理

采用重庆博精医学信息研究所研制的“运动心力检测仪”(ECCM，专利号01256971.2，第1代产品注册证号:渝药管械(试)字99第220007)进行心音信号采集，采集的信号最终以wav文件进行保存。采样频率为11025Hz，量化值为8 bit。由于在采集过程中存在一些人为及环境干扰带来的噪声，所以用基于小波的去噪方法对心音信号进行去噪，为进一步进行非线性混沌处理打下了基础。去噪后的正常及二尖瓣狭窄心音信号如图1所示。

2.2 心音信号相空间重构

根据互信息法得到一例正常心音信号的互信息图如图2所示，可知其最佳时延τ=5。

而图3为Cao法求得的E1、E2分布图，由E2的收敛性可进一步证明心音信号的确定非线性，且得最小嵌入维数为m=8。

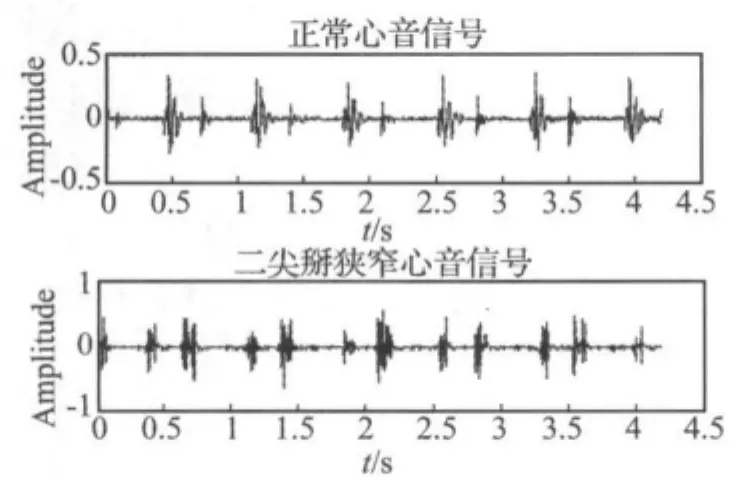
图1 正常及二尖瓣狭窄心音信号Fig.1 The normal heart sound and that with mitral stenosis

图2 正常心音互信息图Fig.2 Mutual information graph of normal heart sound

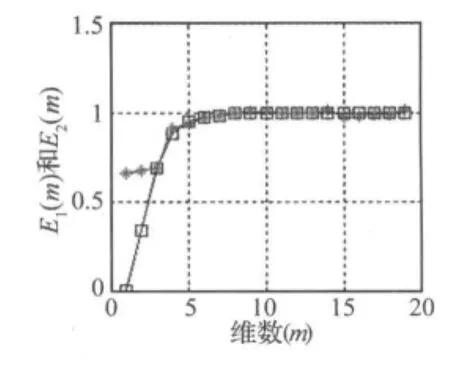
图3 正常心音最小嵌入维Fig.3 Minimum embedding dimension of normal heart sound signal

2.3 心音信号关联维数及最大Lyapunov指数分析

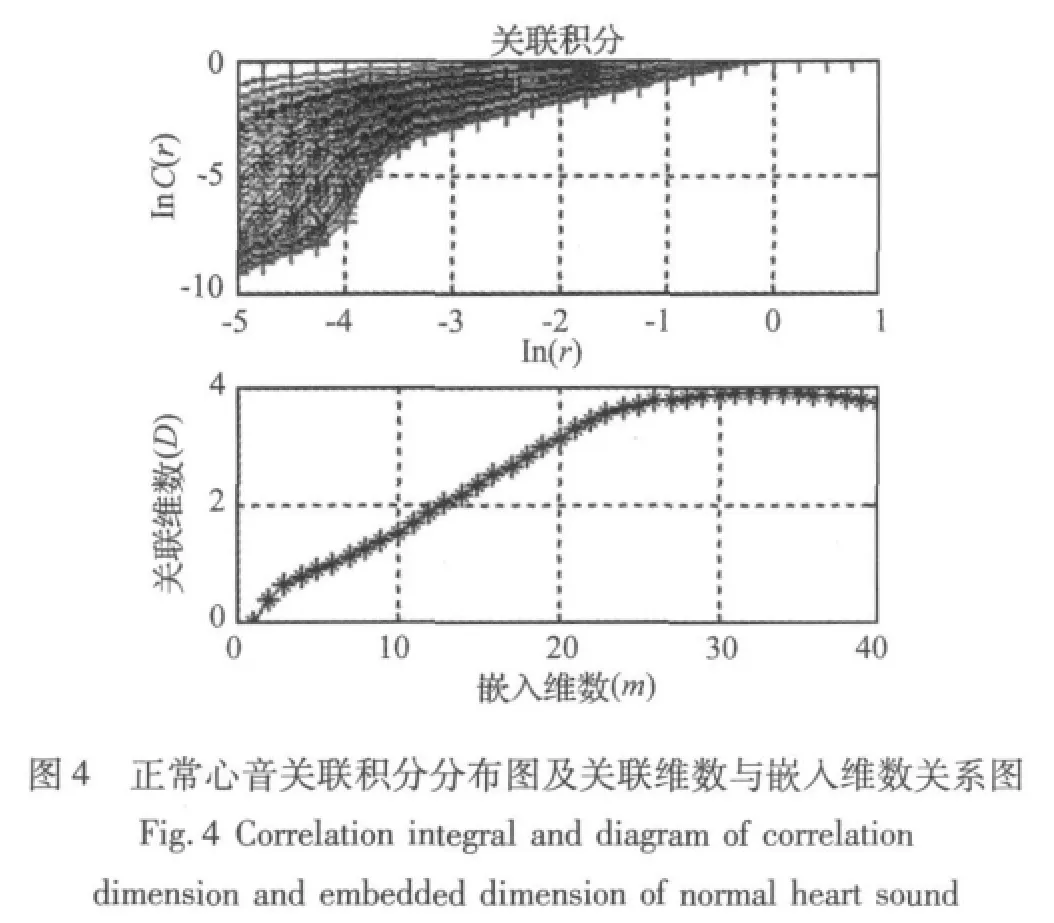
从原始心音信号中截取信号质量较好的几个心动周期，数据长度N=3000，嵌入维数m从1～40变化，延迟时间 τ按互信息量法求得，分别为 6，5，4，7，5，计算出相应嵌入维数下的关联函数Cm(r)，然后做出lnC(r)对ln(r)的分布图。确定关联积分分布图中的标度区，用最小二乘法对标度区域内的点进行线性拟合，计算其斜率得到关联维数。图4是一例正常心音信号的关联积分分布图及关联维数(D)～嵌入维数(m)关系图。由心音信号的关联维数同嵌入维数的关系图可以看出随着嵌入维数的增加，关联维数渐渐收敛于一个稳定值，且为分数，这也进一步证明了心音系统是混沌的。

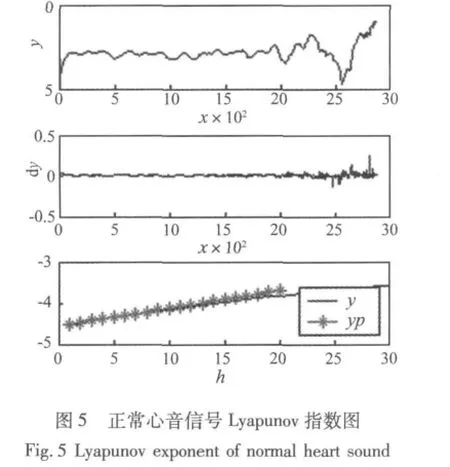
计算心音信号的最大Lyapunov指数，结果如图5所示，最后根据最小二乘法拟合得到的斜率即为最大Lyapunov指数值。

2.4 心音信号递归图

从递归图(图6)可以看出，二尖瓣狭窄心音信号的递归图纹理较正常心音复杂，正常心音表现出较强的周期性，而二尖瓣狭窄心音由于舒张期的心杂音呈现复杂的纹理。

3 结果分析

实验采集了13例正常心音及13例二尖瓣狭窄心音信号，其中二尖瓣狭窄心音信号包括有开瓣音、杂音组合及幅值加大的心音。对这些心音信号的关联维数及最大Lyapunov指数计算结果如表1所示，定量递归分析如表2示，并用SPSS 17.0对结果进行统计分析。

由表1可知，二尖瓣狭窄心音信号的关联维数及最大Lyapunov指数均大于正常心音信号，且通过独立样本t检验可以看出，二尖瓣狭窄心音与正常心音具有显著性差异。

表1 正常及二尖瓣狭窄心音信号的相空间重构参数及混沌特征参数Tab.1 Phase space reconstruction parameters and the chaotic characteristic parameters of normal heart sound and that with mitral stenosis

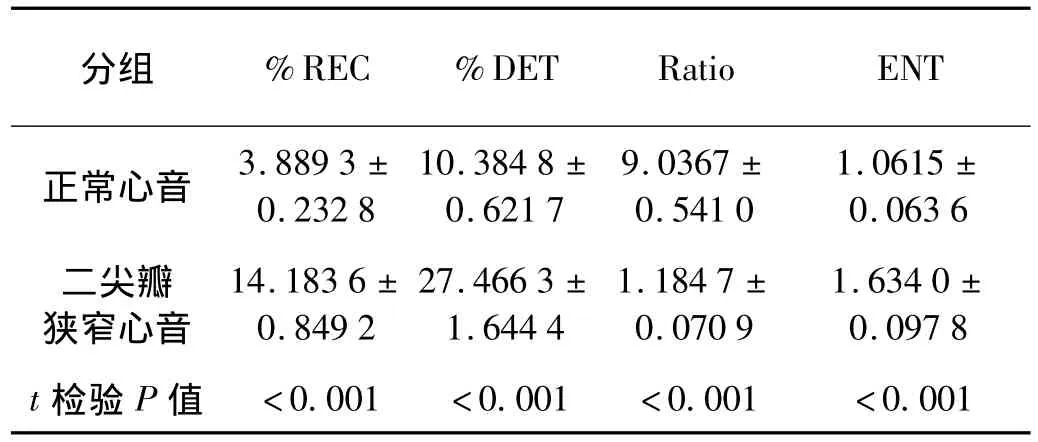
表2 正常及二尖瓣狭窄心音信号的定量递归分析Tab.2 Recurrence quantification analysis of the normal heart sound and that with mitral stenosis

同样地，二者的定量递归分析结果显示，二尖瓣狭窄心音信号的递归率及确定率都明显高于正常心音，而确定率与递归率的比值却远小于正常心音，说明正常心音的随机性更强。另外，正常心音的线段分布熵较低，反映了其递归图的长度分布更均匀，正常心音的递归图也正体现了这个特点，且二者的递归定量分析参数差异显著。

4 结论

混沌特征分析是反映系统非线性及复杂性的有效方法，已广泛应用于心电及脑电等生理信号的分析。本文通过提取心音信号的关联维数、最大Lyapunov指数、递归图及其定量分析参数，分析了二尖瓣狭窄心音信号的复杂性及对应血流动力学状态的改变。从关联维数及最大Lyapunov指数的结果可以看出，二尖瓣狭窄心音信号较正常心音信号要大，且具有显著差异性(P＜0.01)。可以推测，由于瓣膜的狭窄导致心脏血流发生异常而使相应的心音信号变得复杂。另外，递归图有助于定性分析正常及异常心音的差异性，而其定量分析参数对于信号的周期性、随机性、复杂性的反映也有一定的参考作用。

心音信号的混沌动力学分析，对于二尖瓣狭窄的早期诊断提供了新方法。为了该方法能应用于临床检查，还需进一步研究二尖瓣狭窄程度与相应混沌特征的关系，这将是后续研究的内容。

［1］Jandre F C， Souza M N. Wavelet analysis of phonocardiograms:differences between normal and abnormal heartsounds［C］. Proceedings ofthe 19th Annual International ConferenceoftheIEEE， 1997，4:1642－1644.

［2］Wu C H，Lo C W，Wang J F.Computer-aided analysis and classification of heart sounds based on neural networks and time analysis［J］.International Conference on Acoustics，Speech and Signal Processing，1995，5:3455－3458.

［3］Fojt O，Holcik J.Applying nonlinear dynamics to ECG signal processing［J］.IEEE Engineering in Medicine and Biology，1998，17(2):96－101.

［4］Ning X B，Bian C H，Wang J.Research progress in nonlinear analysis of heart electric activities［J］.Chinese Science Bulletin，2006，51(4):385－393.

［5］周 静，何 为.基于关联维数的心音分析研究［J］.现代科学仪器，2007，(2):56－59.

［6］Mayer-Kress G，Yates F E，Benton L，et al.Dimensional analysis of nonlinear oscillations in brain，heart，and muscle［J］.Mathematical Biosciences，1988，90(1 － 2):155－182.

［7］Padmanabhan V，Semmlow J L.Dynamical analysis of diastolic heart sounds associated with coronary artery disease［J］.Annals of Biomedical Engineering，1994，22(3):264－271.

［8］Kumar D，Carvalho P，Antunes M，et al.Discrimination of heart sounds using chaos analysis in various subbands［J］.Biosignals 2009:Proceedings of the International Conference on Bio-inspired Systems and Signal Processing，2009:369.

［9］Li B B，Yuan Z F.Non-linear and chaos characteristics of heart sound time series［J］.Proceedings of the Institution of Mechanical Engineers，Part H:Journal of Engineering in Medicine，2008，222(3):265－272.

［10］席晓萍.超声心动图、心电图诊断二尖瓣狭窄左房扩大的对比研究［J］.浙江中医药大学学报，2008，32(3):342－343.

［11］刘 兵，李 桥.二尖瓣狭窄杂音可视化心音图与超声对照研究［J］.生物医学工程研究，2005，24:53－54.

［12］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2001.

［13］Packard N H，Crutchfield J P，Farmer J D，et al.Geometry from a time series［J］.Physical Review Letters，1980，45(9):712－716.

［14］陈 铿，韩伯棠.混沌时间序列分析中的相空间重构技术综述［J］.计算机科学，2005，32(4):67－70.

［15］Fraser A M，Swinney H L.Independent coordinates for strange attractors from mutual information［J］.Physical Review A，1986，33(2):1134－1140.

［16］Cao L Y.Practical method for determining the minimum embedding dimension of a scalar time series［J］.Physica D:Nonlinear Phenomena，1997，110(1－2):43－50.

［17］Grassberger P，Procaccia I.Measuring the strangeness of strange attractors［J］.Physica D:Nonlinear Phenomena，1983，9(1－2):189－208.

［18］Eckmann J P，Kamphorst S O，Ruelle D.Recurrence plots of dynamical systems［J］.Europhysics Letter，1987，4(1):973－977.

［19］Zbilut J P，Webber J，Charles L.Embeddings and delays as derived from quantification of recurrence plots［J］.Physics Letters A，1992，171(1):199－203.