基于EMD的胶合板损伤声发射信号特征提取及神经网络模式识别

徐 锋，刘云飞

(南京林业大学 信息科学技术学院，南京 210037)

声发射(Acoustic Emission，AE)是材料受外力或内力作用产生变形或断裂时，以弹性波的形式释放应变能的现象［1］。目前AE技术已被应用于多个领域，但对胶合板的损伤监测，AE技术鲜有报道。胶合板的损伤模式主要包括基体开裂、纤维断裂、脱胶、分层等，每一种损伤都对应特定的AE信号。然而，不同的损伤模式通常以组合形式出现，类别特征相互重叠［2］，同时由于传播介质的各向异性和多源性噪声的污染，加大了AE信号鉴别的难度。因此，提取各声源信号特征与识别其损伤模式是AE技术应用的首要任务和核心技术。

文献［3］应用短时傅里叶变换对机械故障AE信号进行特征提取，但此方法只适合分析所有特征尺度大致相同的信号，窗口没有自适应性，分析非平稳的AE信号不够理想。文献［4－5］分别利用小波包变换对AE信号进行多层分解，构建以各频段能量序列为表征各损伤或故障信号的特征向量，其缺陷是小波基选择困难，分解层数难以确定。

经验模态分解(Empirical Mode Decomposition，EMD)是一种非常适合于非线性、非平稳信号的分析方法，其本质是对信号进行平稳化和线性化处理，把复杂的信号分解成有限个瞬时频率有意义、幅度或频率受调制的本征模态分量(Intrinsic Mode Function，IMF)。EMD技术现已广泛应用于海洋波动数据分析、设备诊断学和医学诊断学等研究领域［6－8］，并且取得了不错的效果，但在AE信号处理尤其是木质材料激发的AE信号处理方面国内外研究甚少。人工神经网络是由大量的人工神经元相互连接而成的非线性动力系统，近年来研究发现，人工神经网络可对数据量多、特征复杂的信号提供准确度较高的自动分类能力。

基于以上原因，本文提出基于EMD和BP神经网络相结合提取AE信号特征和识别的方法。该方法首先对滤波后的信号进行EMD分解;然后对得到的IMF分量进行筛选，以得到包含主要信息的分量组成，再计算各IMF分量能量占比，构建各损伤信号对应的特征向量;最后依此向量作为神经网络的输入样本建立神经网络分类器，实现对胶合板各损伤类型的识别。

1 基于经验模态分解的能量提取算法

EMD是把一个复杂的非平稳信号分解为有限个IMF和一个残余函数之和的形式，即:

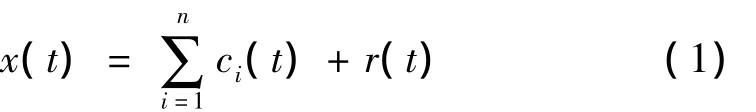
式中:r(t)为残余函数，它是一单调函数，ci(t)为各个IMF分量，并满足以下两个条件:

(1)在整个数据段，极值点的个数和零交叉点的个数必须相等或相差不能超过一个;

(2)在任何一点，由局部极大值点形成的包络线和局部极小值形成的包络线的平均值为零。

1.1 基于IMF能量的特征提取

EMD是依据信号本身的局部特征信息进行自适应的分解方法，分解得到的各个IMF分量既包含了信号的局部特征，也包含了不同的时间尺度信息，从而通过不同分辨率表达信号的特征信息，并精确地给出信号能量随频率和时间的联合分布情况［9－10］，即各频带能量的变化表征了各种信源的特征。因此，本文提取各尺度下IMF的能量占比作为各信号特征来识别声源类型。基于IMF能量的特征提取步骤:① 对原始信号进行EMD，选取包含主要信息的前n个IMF分量;② 求各IMF的能量Ei:

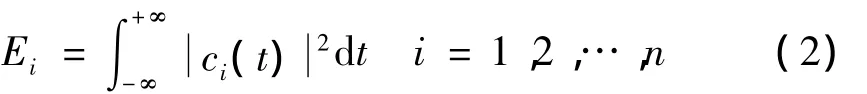
③ 以能量比为元素构造一个向量 T=［E1/E，E2/E，…，En/E］，此向量即表征了信号的特征。其中:

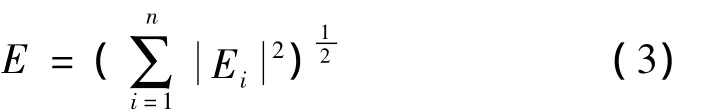
1.2 IMF选择原则

EMD分解不可避免的会出现过分解现象，即得到的分量个数比原信号实际组成分量多，也即出现所谓的虚假分量。过分解产生的原因很多也很复杂，目前一般认为跟EMD的算法、信号长度的有限以及终止筛选的标准有关。一般来说，信号越复杂，虚假分量的个数可能会越多，对后续信号的时频谱分析和进一步的处理越会产生不利影响。原则上，经EMD得到的各个模式分量ci(t)应分别对应于原信号各实际组分，然而由于前述原因，两者之间总存在误差，其差值即形成虚假分量。分析可知，各分量虽不等同实际组分，但必是后者的近似，即两者存在一定的相关性;而虚假分量由两者差值形成，相关性必然很小。因此，从各分量与原信号相关分析中应能分辨出其真伪。另据统计分析理论，因子的方差贡献率是衡量因子重要性的关键指标，该值越高，说明相应因子的重要性越高。于是分别定义各模态分量与原信号的互关系数和其方差贡献率:

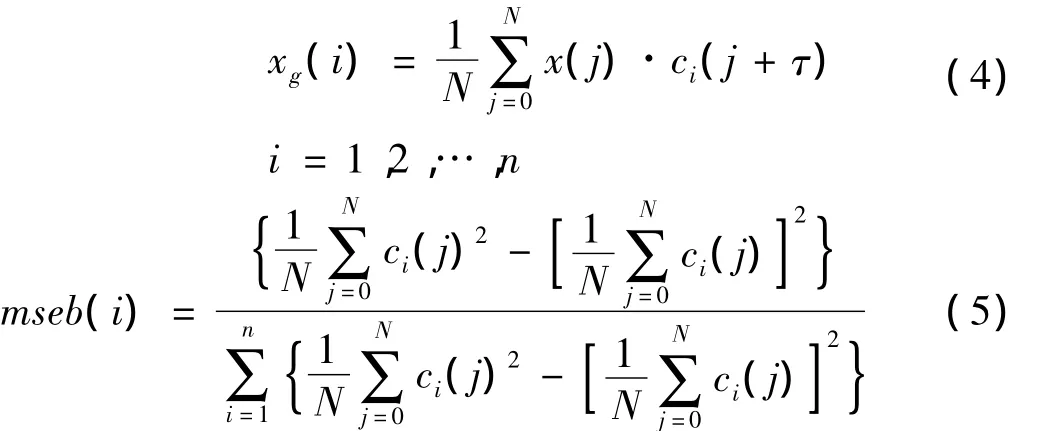
式中:xg(t)和mseb(i)分别为第i个IMF分量与原信号x的互关系数和方差贡献率，N为信号长度，n为IMF分量个数，τ为时间间隔。

本文即根据分量的相关系数和方差贡献率的大小来选取包含主要特征的各IMF分量。

2 人工神经网络模式识别方法

2.1 神经网络的选择

人工神经网络是一个高度非线性的自适应并行分布处理信息系统，其信息处理由神经元之间的相互作用来实现。信息的存贮表现为神经元之间的物理联系。网络的学习取决于神经元连接权系的动态演化过程。神经网络的类型多种多样，但和模式识别结合最成功的是多层前馈网络，即BP网络［11］，本文即选之进行模式识别。

2.2 BP网络结构的设计

由BP定理可知，一个带S型激活函数的三层BP网络，只要隐节点数足够多，就能以任意精度逼近有界区域上的任意连续函数，即一个三层BP网络就能完成任意的n维到m维的映射。BP神经网络最重要的是隐含层的确定。虽然隐层神经元数目选择不存在一个理想的解析式，但其节点数目与问题的要求、输入、输出单元的数目都有着直接关系。综合现有文献，隐含层节点数近似计算公式为:

式中:k为隐层节点数;n为输入节点数;m为输出节点数;a是［0，10］之间的常数。输入层节点数一般由一组特征值样本的数据量决定，输出层节点数可取类别数x或log2x。

2.3 训练函数的选择

采用不同的训练函数对网络的性能会有影响，比如收敛速度等。本文应用各种典型训练函数对网络进行训练，观察各种训练算法的收敛速度和误差，最后确定Levenberg-Marquardt算法为本识别的最优训练函数。

3 实验与分析

3.1 实验方法［12］

试验对普通胶合板强度进行测试研究。样品采用“兔宝宝”牌5层胶合板，其内部为杂木夹芯，外覆桃花芯面板，由环保脲醛胶粘合而成。试样(如图1所示)按GB/T9846.9－1988定义的普通胶合板力学性能测试试件方法锯制，尺寸为100mm×25mm×5mm。试验测试温度为25℃，样品为气干状态。加载系统为深圳新三思公司SANS－CMT6104台式万能试验机;采集系统选用美国PAC公司的PCI－2声发射采集系统，用两个宽带传感器S9208组成线定位阵列方式，同时采集各个波击的波形。

试验中为保证传感器与材料表面良好耦合，选用真空润滑脂作为耦合剂，传感器用透明胶带固定在试样的表面。试样两端夹紧于试验机的一对活动夹具中，使成一直线，试样中心通过夹具的轴线，拉伸沿试样长度方向上进行，等速加荷，速度为3mm/min，最大破坏荷重的读数精确到5 N，拉伸过程在准静态条件下进行，直到试样断裂为止。拉伸模型见图2。

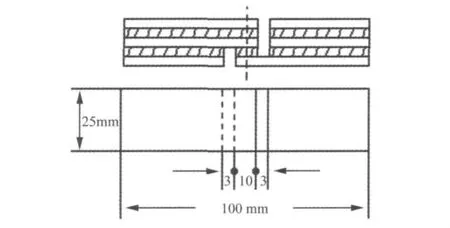
图1 五层胶合板拉伸试样图Fig.1 Five-plywood tensile specimen

3.2 胶合板加载声发射信号特征分析

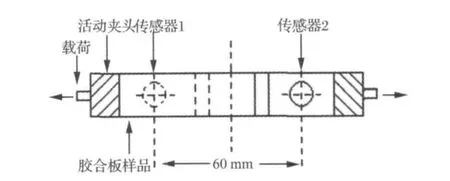
图2 五层胶合板拉伸模型示意图Fig.2 Tensile loading model of five-plywood

对于厚度方向尺寸远小于其他两个方向的板而言，相应于一定的激励条件，在其中主要形成的是板波(Lamb波)。由文献［13－14］可知，受激励后，板中存在多种模式的板波，但当板厚远小于波长时，主要以两种模式的波为主，即最低阶的对称波S0和最低阶的反对称波A0。前者即是膨胀波，其传播速度为一定值，没有频散效应;后者亦称弯曲波，其传播速度与角频率的平方根成正比，有频散效应。一般情况下，板中的波是这两种波的组合(互相耦合)。研究发现［13］当激励力源作用方向与板平面垂直时，在板中主要产生的是弯曲波，而当力源方向平行板方向时，主要是膨胀波。通常，膨胀波的高频成分要比弯曲波丰富。胶合板受载形变作为强声发射源，其声源有基体开裂、脱胶、分层和纤维断裂等。理想上，纤维断裂总在平面内完成，类似沿板平面方向的力源，因此，激发的AE信号应以膨胀波为主，无频散效应;而分层损伤则明显沿板厚方向发生，类似于垂直板平面方向的力源，因此，所激发的声信号波型当以弯曲波为主，存在频散现象;基体开裂、脱胶产生的AE信号，其特征介于两者之间，一般应同时表现为膨胀波和弯曲波两种组合形式。

3.3 实验结果分析

由实验得知，AE源主要集中在主损伤区或断裂部位。考虑到声源的位置、材料物理特性及波的传播对类别特征的复杂影响［2］，将所有样本取自主损伤区宽20mm范围内的事件。图3分别是胶合板拉伸基体开裂、脱胶、分层和纤维断裂为主导的典型时域信号(已按文献［15］去噪)。采样频率为2 MHz，单个AE信号采样长度为2048点。本文以图3(a)为例详细讲解特征提取过程，其余损伤信号特征提取过程类似，列于表1。

图3 五层胶合板拉伸损伤信号波形Fig.3 Waveform of damage signals from stretched five-plywood

表1 五层胶合板损伤信号各特征向量Tab.1 Eigenvectors of damage signals from stretched five-plywood

对图3(a)信号作EMD分解，共得到10个IMF分量和1个残余量(图4所示)。按节1.2方法，分别计算各IMF分量与原信号互相关系数和各自的方差贡献率，统计图见图5所示。研究发现，随着分解阶次递增到一定程度，各分量和原信号的互关系数和方差贡献率会急剧地减小。如IMF6与原信号的互关系数为0.0320，方差贡献率为0.4823%，而IMF8与原信号的互关系数则达1e－4级，趋近于零。多次实验表明，对于相关系数小于0.03的IMF分量，其方差贡献率不足2%，而从剩余分量的能量来看(见图6所示)，其值也极小。因此，可认为互关系数小于0.03的IMF分量即为虚假分量，应以剔除。按1.1节方法计算经筛选的IMF分量的能量占比(本文分量为6个)，以此作为表征损伤信号的特征向量，结果示于表1。

对比表1各信号特征可知，基体开裂与脱胶信号频率丰富，频段较宽，为膨胀波和弯曲波模式组合。一般来说，基体多为杂木，脆性较强，其剪切强度小于胶层强度，因此频率更高。而脱胶信号弯曲波模式占主导，频率稍低，从失效样品查看，明显存在分层和滑移现象，和3.2节分析基本一致。

纤维断裂频率较高且单一，无频散现象。在胶合板工艺过程中，由于木质纤维束张力不均匀以及纤维表面的惰性，使得界面的强度很低。这些初始缺陷，在胶合板承载负荷时发生复合形式的细观破坏。随着拉伸应力的加大，其发展和累积的结果导致材料的损伤加剧，纤维开始发生不同时断裂，造成应力的波动和重新分布，从而加速了周围基体和界面的进一步破坏。至破坏后期，纤维束对承拉起主要作用，随着断裂数量的增多，剩余纤维无法承受过大的拉伸载荷，因而发生整体断裂。结合样品断口纹理分析，断裂主要沿垂直于纤维方向扩展，呈剪切断裂方式，波形以膨胀波为主导。

由表1可知，信号类别特征虽有不同程度的重叠，但本文方法提取的信号特征甚为明显，显示出较强的鉴别能力。以此特征向量作为样本，可为后续使用神经网络进行识别提供依据。

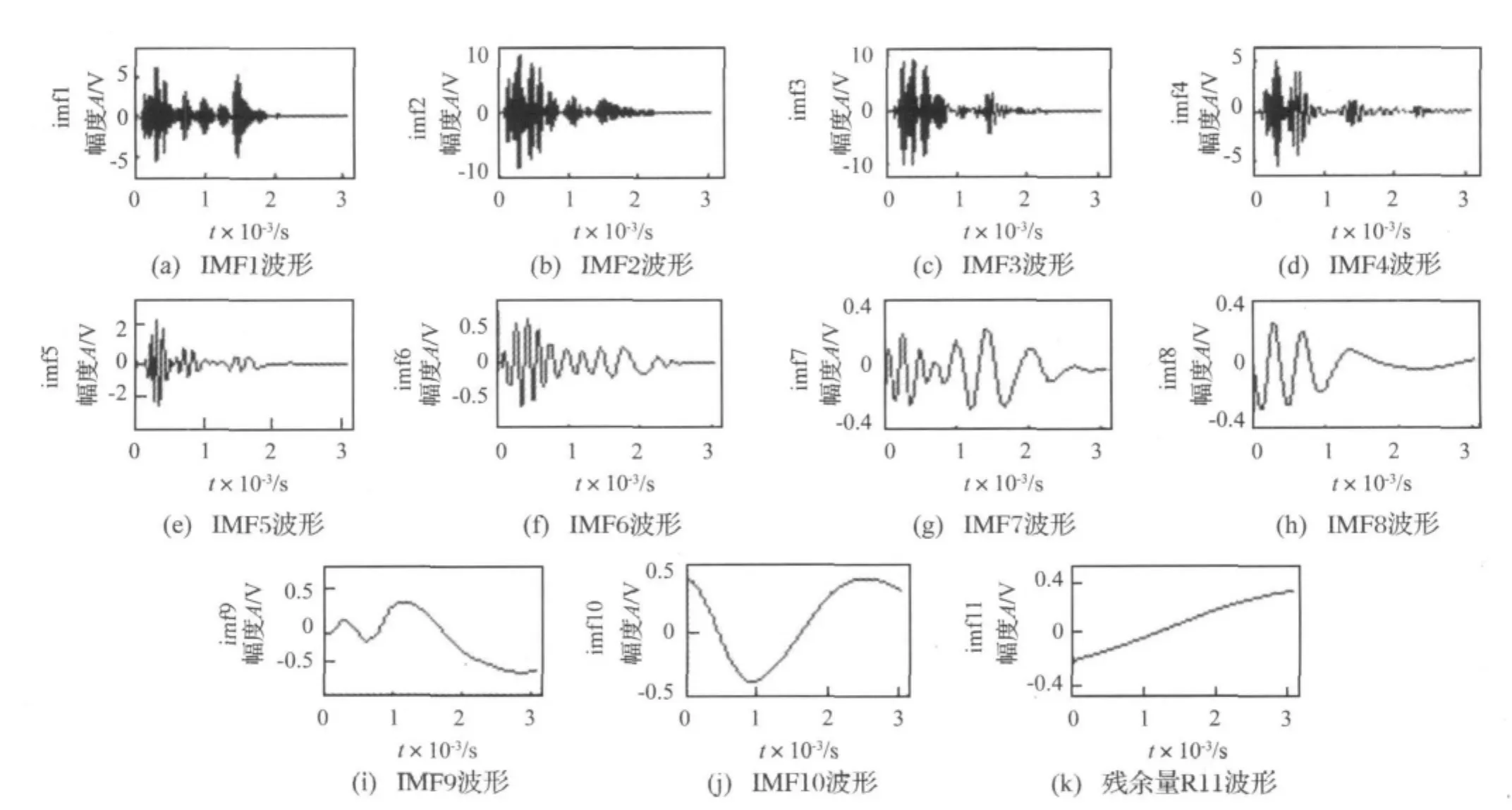
图4 基体开裂声发射信号EMD分解结果Fig.4 Results of EMD of AE signal of plywood matrix cracks

图5 各阶IMF分量与原信号互关系数及方差贡献率Fig.5 Cross correlation coefficient and variance contribution ratios

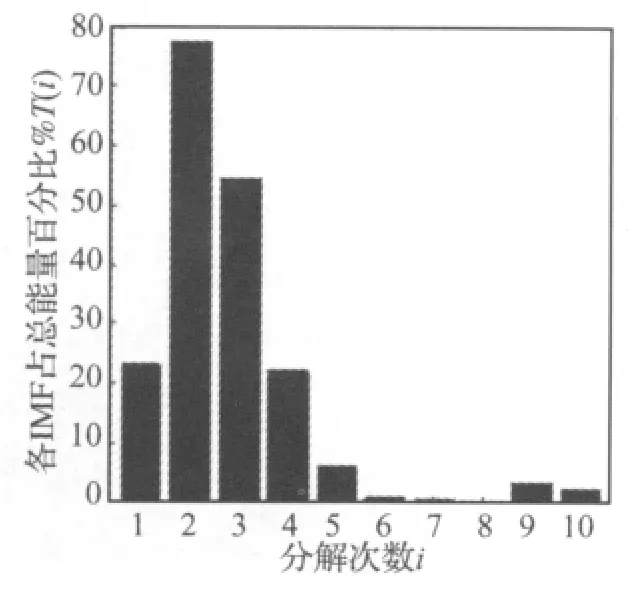
图6 各阶IMF分量能量比率Fig.6 Energy ratios of IMF

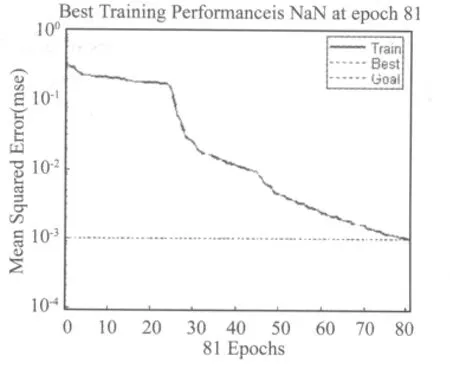
图7 网络训练误差变化曲线Fig.7 Curve of network training error

3.4 模式识别

把各特征向量作为BP网络的训练输入样本。样本包含胶合板基体开裂10组、脱胶8组、分层12组和纤维断裂10组共计40组。BP网络输入节点为6，输出节点为2，层数为3，隐层节点为7，隐含层采用双曲正切S型激活函数，输出层采用对数S型激活函数。网络在经过81次训练后达到设定的最小期望误差0.001(见图7)。用网络对训练数据进行识别，识别正确率达到100%。证明该网络具有较强的学习能力，能够按照给定的输入输出正确建模。

为检验网络的实际应用性能，用该网络对118组测试样本(脱胶30组、纤维断裂30组、分层28组和基体开裂30组)进行检验，识别正确率达到93.6%，这表明该人工神经网络的范化能力较高，设计结构合理，达到自动识别AE信号类别的目标。

为进一步比较本文方法的优越性，对同样的训练和测试样本使用文献［16］方法进行识别，识别成功率为91.2%，说明对AE这种非平稳、非线性信号，EMD方法比小波方法有更好的自适应性，且小波分析结果还取决于小波基选取和分解层次的问题，不同的小波基和分解层次，识别结果明显不同。

4 结论

针对胶合板损伤AE信号的非线性、非平稳性和损伤类别特征相互重叠的实际，提出基于EMD的特征提取方法。以分解得到的IMF分量的能量比率构建表征损伤的特征向量，并对分解中产生的虚假分量采用互关系数和方差贡献率来予以剔除，最后结合BP神经网络对胶合板损伤模式进行识别。

(1)EMD方法基于信号的局部特征时间尺度，是依据信号本身的信息进行的分解，是自适应的信号处理方法，非常适合非线性和非平稳过程。信号经EMD分解后所得的IMF分量突出了原信号不同的局部特征信息，有利于损伤信号的特征提取;

(2)理论分析和实验结果表明，根据IMF分量的相关系数和方差贡献率的大小来选取各主要IMF分量并以此作为表征损伤信号的特征向量是切实可行的;

(3)基于EMD和BP神经网络的声发射信号特征提取和识别方法能够有效地提取信号的特征，实现对胶合板各损伤类型较为准确的识别，并且这一方法比基于小波－BP神经网络的特征提取与识别方法准确率更高，说明EMD方法比小波方法对非平稳、非线性信号有更好的自适应性。

由于木质胶合板的声发射研究国内开展的不多，对该类材料的声发射特征的分析及识别还待进一步研究，尤其对多层胶合板声发射特征的定量研究还有待于大量实验数据的积累和归纳。

［1］袁振民，马羽宽，何泽云.声发射技术及其应用［M］.北京:机械工业出版社，1985.YUAN Zhen-min， MA Yu-kuan， HE Ze-yun. Acoustic emission technology and application［M］.Beijing:Machinery Industry Press，1985.

［2］徐 锋，刘云飞.基于中值滤波－SVD和EMD的声发射信号特征提取［J］.仪器仪表学报，2011，32(12):2712－2719.XU Feng， LIU Yun-fei. Feature extraction of acoustic emission signals based on median filter－ SVD and EMD［J］.Chinese Journal of Scientific Instrument，2011，32(12).

［3］廖传军，李学军，刘得顺.STFT在AE信号特征提取中的应用［J］.仪器仪表学报，2008，29(9):1862 －1867.LIAO Chuan-jun，LI Xue-jun，LIU De-shun.Application of STFT in feature extraction of acoustic emission signal［J］.Chinese Journal of Scientific Instrument，2008，29(9):1862－1867.

［4］邓 扬，丁幼亮，李爱群.基于小波包分析的拉索损伤声发射信号特征提取［J］.振动与冲击，2010，29(6):154－158.DENG Yang，DING You-lang，LI Ai-qun.Feature extraction of acoustic emission signals for cable damage based on wavelet packet analysis［J］.Journal of Vibration and Shock，2010，29(6):154－158.

［5］赵元喜，胥永刚，高立新，等.基于谐波小波包和BP神经网络的滚动轴承声发射故障模式识别技术［J］.振动与冲击，2010，29(10):162 －165.ZHAO Yuan-xi，XU Yong-gang，GAO Li-xin，et al.Fault pattern recognition technique forrollerbearing acoustic emission extraction based on harmonic wavelet packet and BP neural network［J］.Journal of Vibration and Shock，2010，29(10):162－165.

［6］张 超，陈建军，郭 迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法［J］.振动与冲击，2010，29(10):216－220.ZHANG Chao，CHEN Jian-jun，GUO Xun.A gear fault diagnosis method based on EMD energy entropy and SVM［J］.Journal of Vibration and Shock，2010，29(10):216－220.

［7］王玉静，宋立新，康守强.基于EMD和奇异值分解的心律失常分类方法［J］.信号处理，2010，26(9):1423 －1427.WANG Yu-jing， SONG Li-xin， KANG Shou-qiang.Arrhythmia classification based on empirical mode decomposition and singular value decomposition［J］.Signal Processing，2010，26(9):1423－1427.

［8］王军栋，齐维贵.基于EMD－SVM的江水浊度预测方法研究［J］.电子学报，2009，37(10):2130 －2133.WANG Jun-dong， QI Wei-gui. Prediction of river water turbidity based on EMD-SVM［J］.Acta Electronica Sinica，2009，37(10):2130－2133.

［9］Huang N E，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454:903 －995.

［10］Huang N E，Shen Z，Long S R.A new view of non － linear water waves:The Hilbert spectrum［J］.Annu.Rev.Fluid Mech.1999，31(3):417 －457.

［11］毛汉颖，成建国，黄振峰.基于BP神经网络的金属裂纹声发射信号特征参数的提取［J］.机械设计，2010，27(2):84－86.MAO Han-ying， CHENG Jian-guo， HUANG Zhen-feng.Collection on characteristic parameters of emitted signals of metal cracking sound based on BP neural network［J］.Journal of Machine Design，2010，27(2):84－86.

［12］陆仁书.胶合板制造学(第2版)［M］.北京:中国林业出版社，1993:10－23.LU Ren-shu.Plywood manufacturing science(2nd Ed)［M］.Beijing:China Forestry Publishing House，1993:10 －23.

［13］耿荣生，沈功田，刘时风.基于波形分析的声发射信号处理技术［J］.无损检测，2002，24(6):257 －261.GENG Rong-sheng， SHEN Gong-tian， LIU Shi-feng.Acoustic emission signal processing technique based on waveform analysis［J］.Nondestructive Testing，2002，24(6):257－261.

［14］Lowe M JS， DiligentO.Low－ frequencyreflection characteristics of the S0Lamb wave from a rectangular notch in a plate［J］.Acoustical Society of America，2002，111(1):64－74.

［15］徐 锋，刘云飞.基于中值滤波－奇异值分解的胶合板拉伸声发射信号降噪方法研究［J］.振动与冲击，2011，30(12):135－140.XU Feng， LIU Yun-ei. Research on noise reduction of acoustic emission signals generated from plywood stretching based on median filter－ singular value decomposition［J］.Journal of Vibration and Shock，2011，30(12):135－140.

［16］徐 锋，赵明忠，刘云飞.胶合板声发射信号的小波包特征提取及神经网络模式识别［J］.现代电子技术，2011，34(21):96－99.XU Feng， ZHAO Ming-zhong， LIU Yun-fei. Feature extraction and pattern recognition of acoustic emission signals of plywood［J］. Modern Electronics Technique，2011，34(21):96－99.