基于结构构形易损性理论的桁架结构分析

苏冠兴，张志强，叶继红

(1.东南大学 土木工程学院，南京 210096;2.江苏省苏科建设技术发展有限公司，南京 210008;3.东南大学 混凝土及预应力混凝土结构教育部重点实验室，南京 210096)

如果一个结构在某种局部破坏作用下所产生的后果是整个结构大范围的破坏，则称该结构就是易损的;反之，如果一个结构在一定程度上能够承受任意的局部破坏作用，则称该结构就是不易损的或是鲁棒的(强健的)。可以认为，结构的局部破坏引起的整体破坏范围越大，结构的易损性就越大。越来越多的专家认为:为了保证结构的安全，设计中必须考虑结构的易损性问题。在建立结构易损性和鲁棒性理论方面各国学者提出了不同的概念和方法，Lind［1］提出了基于概率的易损性和容许损伤的定义义，易损性定义为损伤系统的失效概率与未损伤系统的失效概率的比值，而容许损伤定义为易损性的倒数。Ziha［2］通过引入不确定测度的概念，提出了基于不确定性信息熵的事件系统鲁棒性理论，指出提高系统的鲁棒性要求有效模式和失效模式的概率分布尽量一致均匀。Beedy［3］提出了基于能量吸收思想的鲁棒性概念和单位体积允许损伤能量的概念，结构鲁棒性的要求就是指能够吸收由意外事故造成的损伤而不发生倒塌。柳承茂等［4］也对易损性问题进行了研究，提出了基于刚度的构件冗余关联度的概念，并在势能最小原理的基础上对构件冗余关联度与结构静不定次数的关系进行了证明。Blockley等［5－13］提出基于结构形式的易损性概念，通过研究结构构件组合的方式和结构可能发生的失效情况，研究结构中的薄弱部位，提出了系统的理论。本文正是基于这种理论研究桁架结构的易损性并与荷载作用相联系［14－15］。

1 基于结构构形的易损性理论

1991年英国布里斯托大学的 Blockley等［5－13］提出了基于结构构形的易损性理论，将易损性定义为部分的损坏引起整个结构不成比例的破坏。它主要研究的是结构形成过程、杆件可能的损害路径和结构的各种破坏模式。定义结构环或结构球为结构最基本的受力单元，结构由结构环(结构球)连接组合而成。首先选取连接能力最大的结构环为基簇，按照连接能力增大的原则，根据集簇规则集成其他杆件，最终与参考簇(大地)相连集成整个结构。集簇规则有最小损坏需求、节点连接度、与参考簇的距离。在集簇过程中结构连接能力是重要的参数，表征了结构承受各种作用的能力。

解簇过程是集簇的逆序，它不是无序进行的，有严格的规则，主要包括是不是参考簇和结构连接能力等。解簇过程中产生了结构分离度、相对损坏需求和易损性指数等重要参数。它们是区别结构失效模式的重要指标。每次解簇得到一个失效事件，直到结构成为机构，所有的失效事件构成一种失效模式。结构共有五种主要的设计者所关心的失效模式:整体倒塌失效模式、最大失效模式、最易发生失效模式、最小失效模式和特定失效模式。其中，整体倒塌失效模式结构破坏最大、损坏需求最小、易损性指数最大，是一种最易损的失效模式，其所包含的杆件也是设计者着重关心的。

在这种理论中主要提出了以下的基本概念:

(1)图模型:一系列被看作对象的结构单元和节点组成的集合。每个单元至少连接两个节点。

(2)结构簇:图模型的子集，能够形成结构环，处于结构簇中的对象更紧密地连接在一起。整个结构称为完整簇，结构集簇过程中形成的称为子簇。

(3)结构环:二维结构的基本组成部分，可以抵抗任意方向荷载，如图1所示。

图1 结构环示意图Fig.1 Structural ring

(4)连接能力:衡量结构的一个指标，它与结构类型、连接节点的杆件刚度、结构中杆件连接状态等有关，它分单个节点连接能力、结构环的连接能力和结构簇的连接能力。结构环和结构簇的连接能力等于其中所有节点连接能力的平均值。

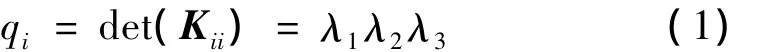
其中:Kii:为节点i的所有杆件刚度矩阵，qi为第i个节点的连接能力。

结构簇的连接能力等于该簇中所有节点连接能力的平均值。Q为结构簇的连接能力，n为结构簇中节点数。

(5)节点连接度:与某结构簇的节点相连的所有杆件数，表征了结构簇与其它簇相连形成新的结构环的潜在能力。

(6)失效事件:由作用引起的结构抵抗某个方向作用能力的丧失，如结构杆件的破坏，节点约束的减小。

(7)损坏需求:每次失效事件对应一定的损坏需求，以衡量引起结构失效作用的大小。失效事件的损坏需求与结构的主轴刚度系数成正比，可以定量的表示如下:

(8)相对损坏需求:一种失效模式的相对损坏需求是其损坏需求与结构最大损坏需求之比。

其中:D表示损害需求;

Dmax表示所有杆件的最大损害需求。

(9)分离度:衡量结构损坏的程度，它是损伤结构连接能力的损失与原结构连接能力之比。当结构成为机构而倒塌时，其分离度等于1。

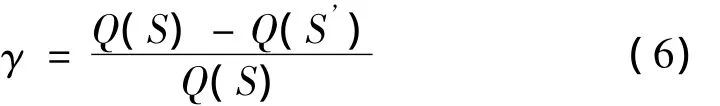
其中:Q(S)表示完整结构的连接能力指标

Q(S’)表示结构损坏后的连接能力指标。

(10)易损性指数:衡量结构的易损性，对一种失效模式它是分离度与相对损坏需求之比，表征了结构分离度与损坏需求不成比例。

其中:Dr表示相对损坏需求;r表示分离度。

(11)整体倒塌失效模式:结构成为机构而倒塌，在所有可能的失效模式中，它的分离度等于1，并且易损性指数最大。

(12)最大失效模式:结构遭受最大范围的损坏但未倒塌，其中，其易损性指数最大。

(13)最小失效模式:结构中具有最小连接能力的簇破坏

(14)最易发生失效模式:所有可能失效模式中，需要最小的损坏需求，所以是结构中最易发生的失效模式。

(15)集簇过程:集簇是基于结构本身构形易损性理论分析的重要过程，它是解簇的基础，其最终所形成的结构层级模型为我们提供了直观的结构形成过程。结构由最基本的节点和杆件组成，由节点和杆件连接成为能抵抗任意方向荷载的结构环(结构球)。这些结构环按照一定规则连接成簇，最终形成整个结构。其中共有五种规则:

① Q:首先也是最重要的规则是连接能力;②Dmin:最小损坏需求;③ N:节点连接度;④ Dis:与参考簇的距离;⑤ FC:当以上四种规则都无效时自由选择。

(16)解簇过程:在集簇过程中，介绍了结构环的退化等级模型及损坏需求的计算。对于集簇后的结构来说，也是一种结构环。可以通过一定的方法找到结构的退化等级和失效杆件，也就是解簇过程。解簇过程以集簇过程为基础，是集簇过程的逆序分析。它使用结构簇的层次等级模型，寻找各失效杆件及各种失效模式。从最高等级的结构簇开始同时分析各结构环，找到失效杆件，称为第一次失效事件。对于破坏后的结构再次集簇和解簇，找到更多的失效事件，直到整个结构或者其中一部分成为机构。

集簇过程从最高等级的结构簇开始依次按下列准则进行:

① 不是参考簇;② 与参考簇形成结构环;③与参考簇直接相连(但是不与其形成结构环);④ 是原始簇而不是中间簇;⑤ 有最小的连接能力;⑥ 有最小的损坏需求;⑦ 最后集成;⑧ 自由选择。

基于结构构形的易损性理论只关注结构本身拓扑关系而与可能承受的荷载无关，最终得到各种可能的失效模式和易损的杆件也不是在特定荷载作用下得到的，它只与结构本身有关，具有普遍性。这种失效模式及易损杆件，可能会在各种特定荷载作用下得到验证。

易损性不同于可靠性，易损性不考虑荷载作用，而可靠性是针对特定荷载作用下结构或构件的安全程度，它与荷载作用密切相关。结构易损性分析用一种简单但有逻辑的方法找到结构中潜在的易损杆件，它与引起结构破坏的各种荷载作用相分离，然而找到结构失效模式之后，设计者就可以评估结构在特定荷载下结构可能的破坏模式，如果这种危险不能承受，就可以采取有效的措施避免。这样的理论补充了安全性和可靠性及风险评估的现有理论。

2 桁架结构易损性分析

由于桁架结构力学简单明了、受力性能良好、自重较轻，被广泛应用于桥梁、屋架、起重机以及大跨屋盖等结构中。本文从国家建筑标准设计图集(05G515)中选取标准平面桁架对其进行结构易损性分析［14－15］。

2.1 桁架－集簇解簇过程

选取15 m跨桁架，其示意图见图2，节点编号见图3，杆件截面见表1，对结构进行易损性分析。

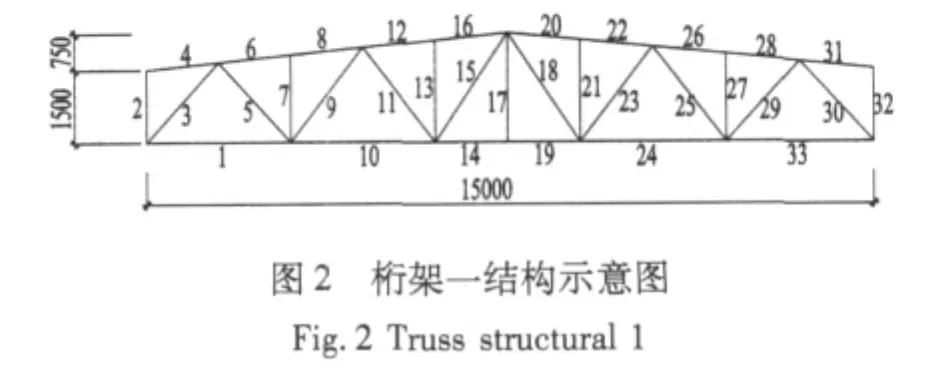
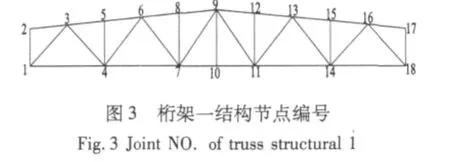
表1 桁架一杆件截面Tab.1 Members section of truss structural 1

按照易损性分析理论，首先计算结构中结构环及节点的连接能力、杆件损坏需求等参数，为集簇解簇过程做准备，计算得到整个结构的连接能力:

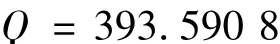
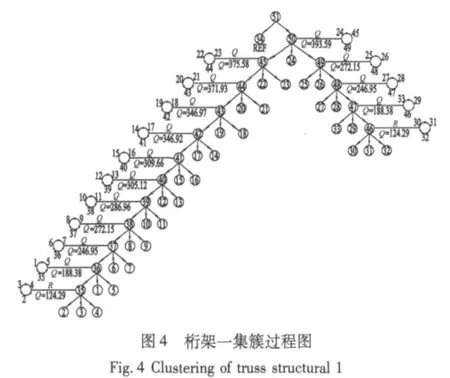
按照结构集簇过程的五种原则，对结构集簇。集成过程及结果如图4所示。对于此结构，连接能力最大结构环是(2、3、4)选取此环为基本簇35，按照连接能力增大的原则逐步集成杆件1、5、6、7等形成结构簇45。此时，如果集成杆件24、25结构连接能力值减小。所以，从剩余杆件中选取结构环连接能力最大(30、31、32)形成簇46，再次按连接能力增大的原则集成形成簇49。此时对杆件24、簇45、簇49集成形成簇50，结构的连接能力值达到390.59。簇50和参考簇34相连，最终形成稳定的簇51。结构集簇完毕。

以簇51为例解簇过程如下:

按解簇的原则对结构解簇，对于簇51解簇过程如图5所示，从簇51开始，簇34是参考簇，所以选取簇50，其由簇49、45、24组成，三个簇都不与参考簇形成结构环，而簇49、簇45与参考簇直接相连，其中簇49有较小的连接能力，选取簇49。下面按照与参考簇直接连连的原则依次选取簇48、47。簇47由簇46、33、29组成，按照选取叶簇的原则，最终确定杆件33首先损坏，称为一个失效事件。此时结构没有形成机构，所以对杆件33损坏后的结构重新集簇解簇，找到杆件32损坏，此时结构称为机构，解簇过程终止。在此种失效模式中包含杆件33、32损坏两个失效事件。

计算结构簇的最大损坏需求如下表。

对簇51解簇最终得到失效事件33、32。计算结构的相对损坏需求，易损性指数如下:

损坏需求:

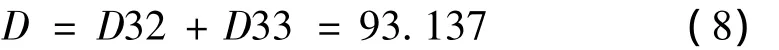
相对损坏需求:

分离度:

易损性指数:

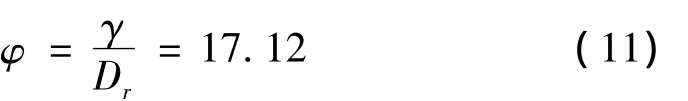
同理，对各簇按照相同的原则集簇解簇，最终找到各种失效模式如表2所示。

以上分析了结构的解簇集簇过程，得到了结构各种失效模式，其中，重要的四种如表3所示。

最易发生失效模式:杆件10、24、33、1的损坏需求最小;最小失效模式:集簇过程中24号(10号)杆最后集成，其破坏后结构仍然为不变体系，分离度不为1;最大失效模式:杆件3、30破坏后，易损性指数最大;整体倒塌失效模式:易损性指数最大，同时分离度为1，失效事件与最大失效模式相同。

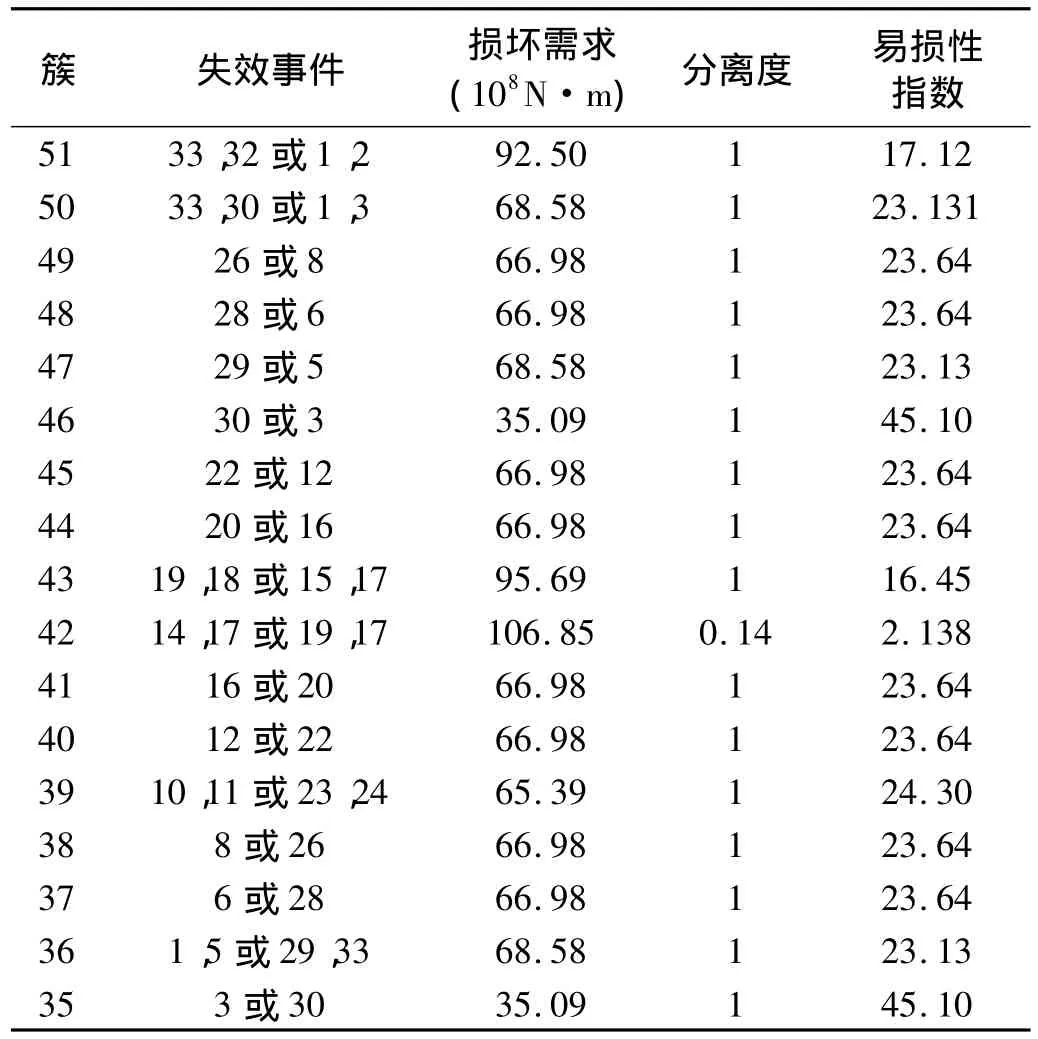
表2 桁架一解簇结果Tab.2 Unzipping results of truss structural 1

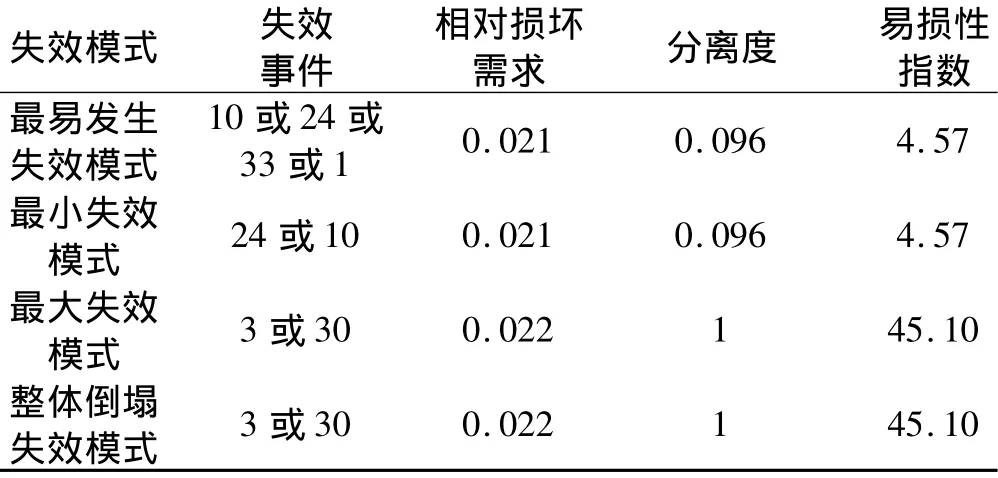
表3 四种失效模式Tab.3 Four different failure scenario

2.2 桁架结构易损性分析结果

从国家建筑标准设计图集(05G515)中再选取四种标准平面桁架对其进行结构易损性分析。其中桁架一、二、三跨度相同，杆件截面不同;桁架四、五跨度不同，杆件截面相同。经过集簇解簇过程求的各桁架的连接能力、损坏需求、分离度和易损性指数等特征参数。最终得到各种失效模式，有五种是最主要的，其中整体倒塌失效模式是设计者重点关注的。表4列出了各桁架的易损性分析结果。

3 失效杆件对比验证

在使用中，桁架主要承受屋面恒载、活载、雪荷载和风荷载等作用。设计中考虑各种荷载组合的影响，取最大值设计杆件截面。本文通过计算桁架杆件内力，求得其应力比。对于应力比较大的杆件其安全储备低，可靠度系数小。对比结构易损性分析结果，发现二者有对应关系。结构应力比计算结果如表5所示。由于结构对称及篇幅所限，表5只列出部分杆件的应力比，对称的杆件应力比大小相同。

表4 桁架易损性分析结果Tab.4 Vulnerability analysis results of truss

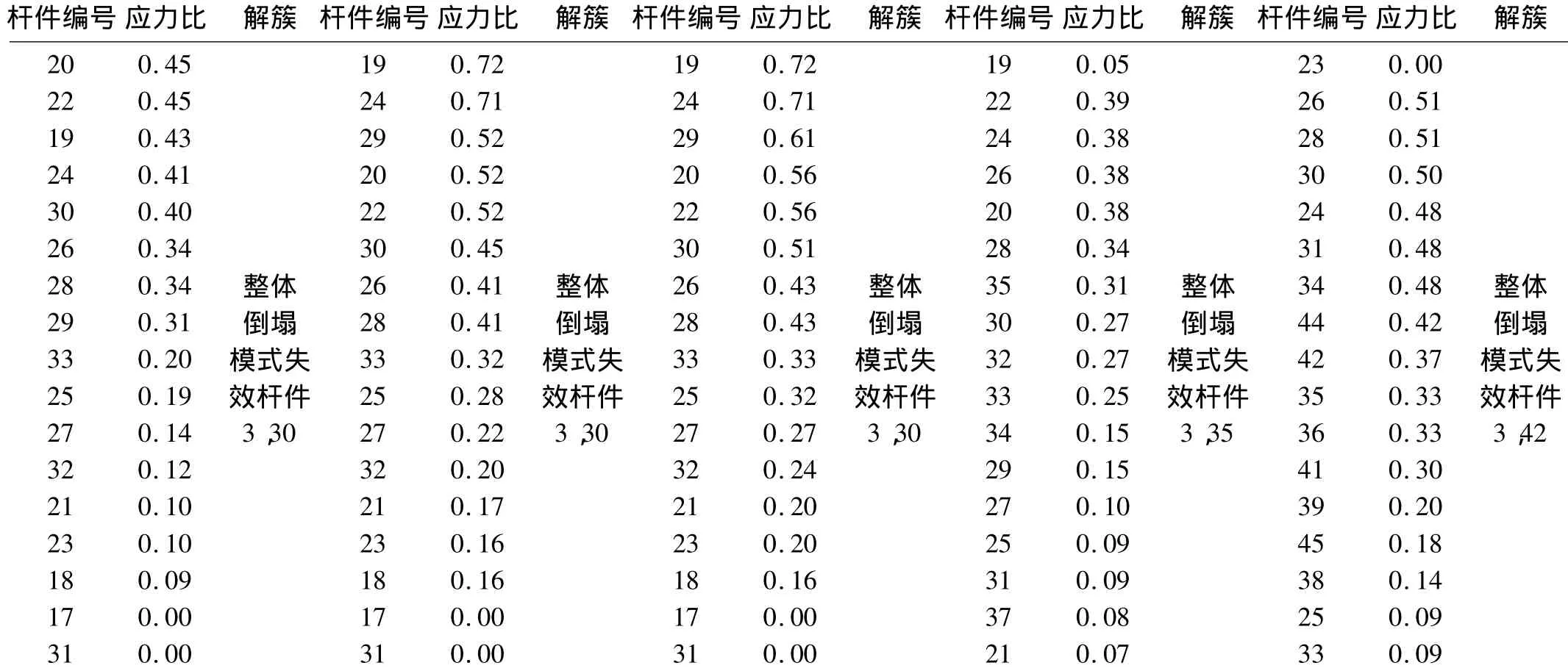
表5 桁架杆件应力分析Tab.5 Stress analysis of truss members

由表5可知，结构易损性分析结果得到的失效杆件(关键杆件)应力同样比较大。例如，对于桁架一整体失效模式的失效杆件是杆3、30，其应力比达到0.40在所有杆件中较大。同时，应力比较大的杆件也是解簇过程得到的失效杆件。例如，对于桁架二应力比最大的杆件是杆19、14，在解簇过程中14、19号杆是簇42解簇得到的关键杆件。

通过以上分析可知，结构易损性分析得到的失效杆件与应力比较大的杆件有对应关系。这些杆件是结构中可靠度较小的、易损的，其损坏后会对结构造成大的破坏。对这些杆件有必要加强其设计，并重点监测。

在结构集簇解簇过程中，要对结构集簇过程的各中间簇进行解簇。对于桁架这种比较小的结构其计算量是可以接受的。然而对于大跨网壳等杆件数量较多的杆件计算量仍然很大。通过以上分析给设计者提供了一种可行的方法，在结构杆件设计过程中必然要计算结构的应力比，对应力比较大的杆件计算其分离度、相对损坏需求、易损性指数等参数，进而判断结构的失效模式，找到整体倒塌失效模式。从而避免了对各中间簇重复集簇解簇。

4 易损性特征参数与极限荷载

对各桁架在跨中施加集中力，考虑材料非线性，得到结构荷载位移曲线。如图6所示。

由图6可以看出，随荷载幅值增加位移曲线切线斜率发生变化，刚度削弱，部分杆件进入屈服破坏。如桁架一:结构在集中力为108 kN时，荷载位移曲线斜率有明显变化，说明此时部分构件进入塑性。在108 kN时，位移幅值为0.0326，为结构跨度的1/460。

由表6可看出:

(1)桁架一、二、三跨度相同，杆件不同，具有相同的结构组成和类似的集簇过程。随着结构连接能力Q、损坏需求Dmax的增加，集中力作用的临界荷载值也逐渐的增加。而随着易损性指数φ增大，临界荷载值逐渐减小，表现了结构的易损性。

(2)桁架一、四、五杆件相同，跨度不同，结构集簇过程完全不同。随着易损性指数φ增大，临界荷载值逐渐减小。对比桁架四和桁架五连接能力增大，而临界荷载值没有增大反而减小。这是因为结构集簇过程完全不同，易损性特征参数与结构屈服临界峰值、临界位移等没有可比性。

图6 桁架荷载位移曲线Fig.6 Stress’s amplitude-maximum joint displacement curve

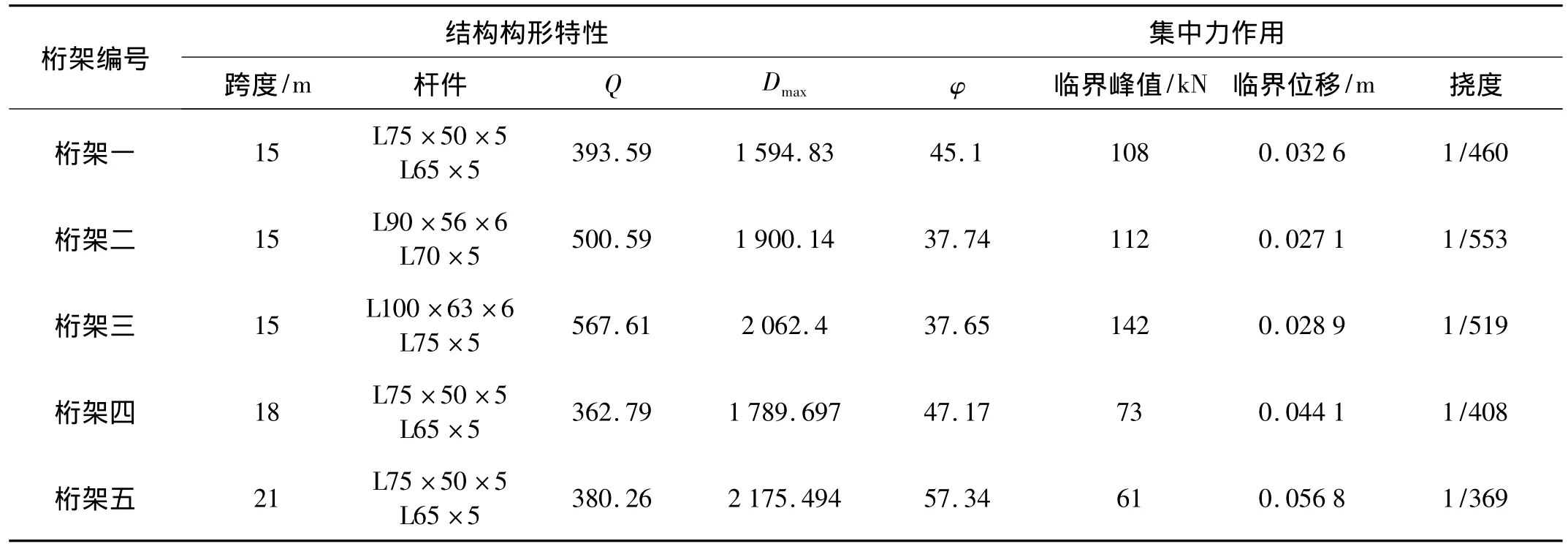
表6 桁架结构各参数表Tab.6 Parameters of truss structural

由以上分析可知，结构杆件、矢跨比、跨度等的变化都会引起结构集簇过程的变化。而对于具有相同的结构组成和集簇过程的结构，易损性特征参数与结构屈服临界峰值、临界位移等有对应关系。结构连接能力增大，屈服临界荷载增大;易损性指数增大，屈服临界荷载减小。如果结构集簇过程不同，则二者没有必然联系，无可比性。

5 结论

通过以上分析可以看出:

(1)基于结构构形的易损性理论自成体系，在分析简单结构(例如桁架)中简单易行，可行性高，通过集簇解簇过程得到了结构的易损性特征参数，及各种失效模式，为判断结构易损性提供了依据。

(2)发现结构应力较大的杆件与易损性分析的失效杆件有对应关系，为大跨网壳等杆件数量多、易损性分析计算量大的结构提供了新的思路，即直接计算应力比较大杆件的易损性参数，找到各种失效模式，判断结构易损性。

(3)通过将集中力作用下结构的临界峰值与易损性分析特征参数对比，发现如果结构形式相同、集簇过程类似，那么随着连接能力的增大结构临界荷载增大，易损性指数增大结构临界荷载减小，结构表现的更易损。如果集簇过程差别很大，则连接能力与临界荷载没有必然联系。

［1］Lind N C.A measure of vulnerability and damage tolerance［J］，Reliability Engineering and System Safety，1995，48:1－6.

［2］Ziha K.Redundancy and robustness of systems of events［J］.Probabilistic Engineering Mechanics，2000，15:347 －357.

［3］Beeby A W.Safety of structures and a new approach to robustness［J］.The Structural Engineer，1999，77(4):16－21.

［4］柳承茂，刘西拉.基于刚度的构件重要性评估及其与冗余度的关系［J］.上海交通大学学报，2005，39(5):746－750.LIU Cheng-mao，LIU Xi-la.Stiffness-based evaluation of component importance and its relationship with redundancy［J］.Journal of Shanghai Jiaotong University，2005，39(5):746－750.

［5］Wu X，Blockley D I，Woodman，et al.Vulnerability of structural systems Part 1:Rings and c1usters［J］.Civil Engineering Systems，1993，10:301－317.

［6］Wu X，Blockley D I，Woodman，et al.Vulnerability of structural systems Part 2:Failure scenarios［J］.Civil Engineering Systems，1993，10:319 －333.

［7］Lu Z，Woodman N J，Blockley D I.A theory of structura1 vu1nerabiJity［J］.The Structura1 Engineering，1999，77(18):17－24.

［8］Blockley D I.Risk based structura1 safety methods in context［J］.Structura1 Safety，1999，21(4):335 －348.

［9］Blockley D I，Heslop S.Managing vu1nerability and risk for sustainability［J］. CivilEngineering and Environment System，2001，18(1):61－86.

［10］Agarwal J，Blockley D I，Woodman N J .Vulnerability of systems［J］.Civil Engineering and Environment System，2001，18(2):141－165.

［11］Agarwal J，Blockley D I，Woodman N J.Vulnerability of 3 －dimensional trusses［J］.Structura1 Safety，2001，23:203 －220.

［12］Pinto J T，Blockley D I，Woodman N J .The risk of vulnerable failure［J］.Structural Satety，2002，24:107－122.

［13］Agarwal J，Blockley D I，Woodman N J.Vulnerability of structural systems［J］.Structural Safety，2003，25(3):263－286.

［14］朱南海，叶继红.基于结构易损性理论的网壳失效模式分析初探［J］.振动与冲击，2011，30(6):248 －255.ZHU Nam-han，YE Ji-hong.Failure scenarios analysis of single-layer latticed domes based on structural vulnerability theory［J］.Journal of Vibration and Shock，2011，30(6):248－255.

［15］苏冠兴.基于易损性理论的结构倒塌模式分析［D］.南京:东南大学，2010.SU Guan-xing.Research on structural failure mechanism based on vulnerability theory，M.S.Thesis，Southeast University，Nanjing，China.2010.