圆钢管含粗骨料超高性能混凝土短柱轴压承载力的正交分析

2021-03-08唐佳军李九阳

人民珠江 2021年2期

唐佳军，王坦，李九阳

(长春工程学院土木工程学院，吉林长春 130012)

一般认为，超高性能混凝土(Ultra high performance concrete, UHPC)包括2种类型：一是不含粗骨料的活性粉末混凝土(Reactive powder concrete, RPC)，二是抗压强度高于100 MPa的含粗骨料超高性能混凝土(Ultra high performance concrete with coarse aggregate, UHPC-CA)[1-2]。以往研究表明，粗骨料的掺入可降低UHPC的收缩变形与成本[3]；粗骨料对高温后UHPC残余抗压强度的提高具有显著作用[4]；粗骨料有利于提升UHPC的高温爆裂性能[5]。因具备良好的力学性能与耐久性能，UHPC-CA的研究已然成为混凝土研究领域的一个热点。

与钢筋混凝土柱相比，钢管混凝土柱具有承载力高、延性好、抗疲劳、耐冲击、施工速度快等优点[6]。闫志刚等[7]通过轴心推出试验研究了圆钢管RPC短柱的界面黏结性能。结果表明：圆钢管RPC短柱的试验现象、破坏形态与荷载-滑移曲线与普通钢管混凝土柱有相似的规律。王一凤等[8]基于ABAQUS软件分析了加载方式(轴压与偏压)和套箍系数ξ对圆钢管RPC短柱受压性能的影响。结果表明，随着ξ的增加，2种加载方式下圆钢管RPC短柱的极限承载力均得到不同幅度的提升。罗华[9]将96组圆钢管RPC短柱的实测数据绘制成Nu/(fcAc)-ξ散点图，利用Origin软件先后进行了线性拟合和多项式拟合，最后提出了圆钢管RPC短柱轴压承载力的一次函数和二次函数的计算公式。戎芹等[10]试验发现，随着ξ的加大，圆钢管RPC短柱的破坏类型由剪切破坏(ξ介于0.63～0.88)转变为腰鼓型破坏(ξ≥1)。可以看出，目前有关圆钢管RPC短柱的研究较多，而缺少圆钢管UHPC-CA短柱的研究。

为此，本文以钢管外径、钢管壁厚、钢材强度和混凝土强度为因素，圆钢管UHPC-CA短柱的轴压承载力为指标，通过直观分析、极差分析、层次分析、因素指标分析、承载力-套箍系数分析和承载力-径厚比分析来研究轴压承载力的变化情况，为后续圆钢管UHPC-CA短柱的试验研究提供参考。

1 试验概况

1.1 试验方案设计

设计L9(34)正交试验方案，选取4个因素：钢管外径(因素A)、钢管壁厚(因素B)、钢材强度(因素C)和混凝土强度(因素D)，每个因素对应3个水平，试验因素与水平见表1。其中，因素A包括102、121、133 mm 3种；因素B的水平有6、8、10 m 3类；因素C的3个水平是Q235、Q345和Q390；因素D的3个水平C130、C150、C180UHPC-CA分别源自杨娟[11]、朋改非[1]和黄政宇等[12]论文中的数据。共设计9组圆钢管UHPC-CA短柱，柱高均为400 mm，试验方案设计见表2，柱立面与断面见图1。

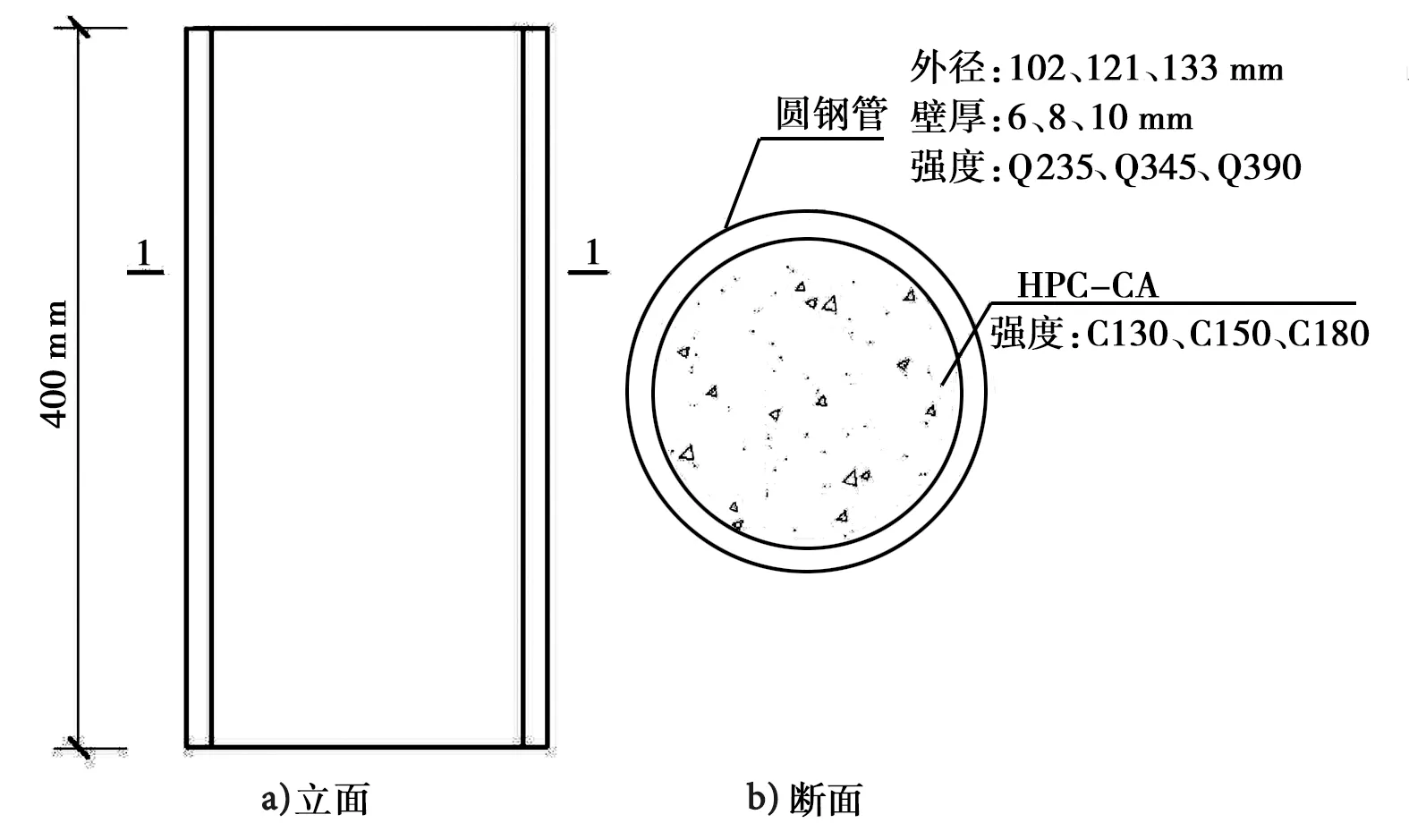
图1 柱的立面与断面

1.2 轴压承载力的计算

本研究采用文献[13]中罗华的基于极限平衡理论的圆钢管RPC短柱极限承载力的计算方法来计算圆钢管UHPC-CA短柱的轴压承载力，计算公式如下：

Nu=fcAc(1+1.188ξ)

(1)

ξ=fsAs/fcAc

(2)

式中Nu——圆钢管UHPC-CA短柱的轴压承载力；fc——UHPC-CA的轴心抗压强度设计值；Ac——钢管内核心UHPC-CA截面面积；ξ——套箍系数；fs——钢材的抗压强度设计值；As——钢管截面面积。

2 试验结果分析

2.1 直观分析

表3示出了各试验组圆钢管UHPC-CA短柱轴压承载力的试验计算结果。由表可知，第1组试件柱的轴压承载力最低，为969.7 kN，此时的正交组合为A1B1C1D1；第9组柱试件的轴压承载力最大，为2 222.8 kN，此时的正交组合为A3B3C2D1。对比分析可以看出，对于C130UHPC-CA，同时提高其钢管外径(102～133 mm)、钢管壁厚(6～10 mm)、钢材强度(从Q235至Q345)，圆钢管UHPC-CA短柱轴压承载力增加了1 253.1 kN，增幅为129.2%，增长效果显著。

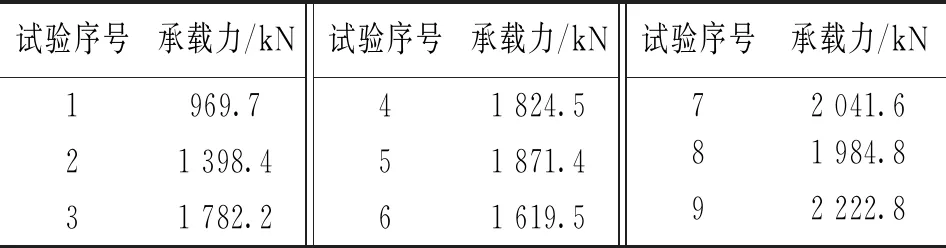
表3 试验计算结果

2.2 极差分析

表4为钢管外径、钢管壁厚、钢材强度和混凝土强度等4个因素对圆钢管UHPC-CA短柱轴压承载力影响的极差值。可以看出，因素A、B、C、D对应的极差值分别为699.7、262.9、373.7和177.3，各因素对轴压承载力的影响由大到小依次为A>C>B>D，即钢管外径>钢材强度>钢管壁厚>UHPC-CA强度。

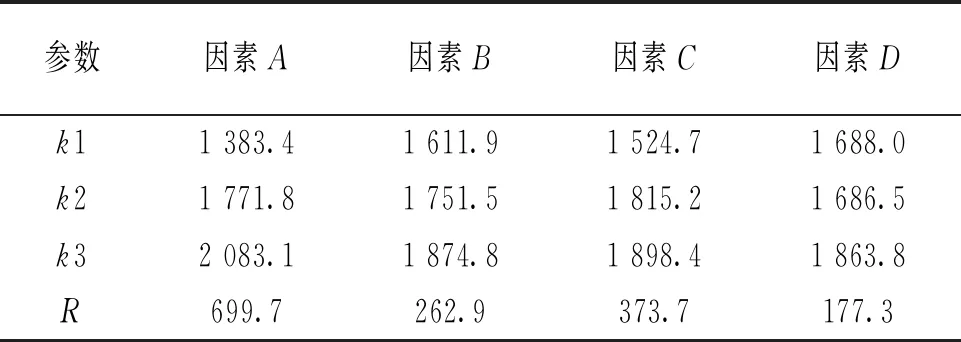
表4 轴压承载力的极差分析

2.3 层次分析

为了得到各因素水平对圆钢管UHPC-CA短柱轴压承载力的影响权重，对研究指标进行层次分析。基于文献[14]中的方法将表4中极差分析计算结果编写成矩阵的形式，并输入MATLAB软件求解，将得到的因素水平对轴压承载力的影响权重值列于表5。

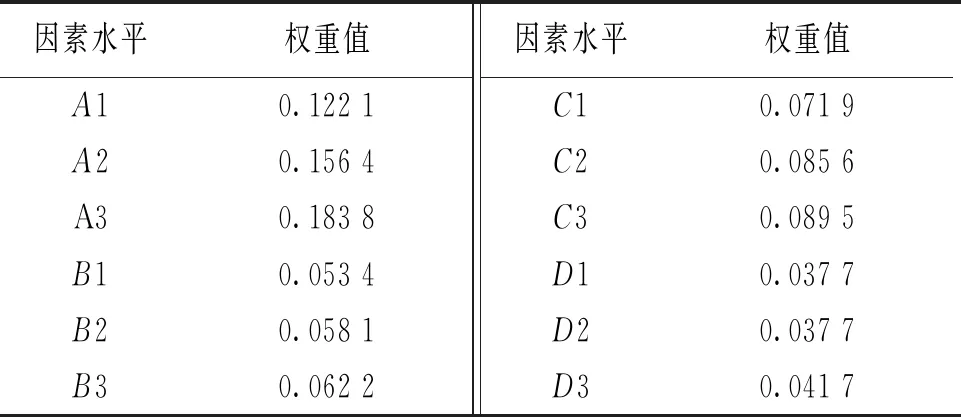
表5 轴压承载力的层次分析

由表5可知，在钢管外径的3个水平中，A3对圆钢管UHPC-CA短柱轴压承载力的影响权重最大，权重值为0.183 8；在钢管壁厚的3个水平中，B3对轴压承载力的影响权重最大，值为0.062 2；在钢材强度的3个水平中，C3的影响权重最大，值为0.089 5；在UHPC-CA强度等级的3个水平中，D3的影响权重最大，值为0.041 7。因此组合为A3B3C3D3，即钢管外径是133 mm、钢管壁厚是10 mm、钢材强度是Q390、UHPC-CA强度是C180时，圆钢管UHPC-CA短柱的轴压承载力将达到最大值。

2.4 因素指标分析

图2示出了圆钢管UHPC-CA短柱轴压承载力随因素水平的变化情况。由图可知，随着因素A、B、C的增长，圆钢管UHPC-CA短柱的轴压承载力均逐渐增加；随着因素D的增加，轴压承载力先略有降低后逐渐增长。当钢管外径由102 mm增长至133 mm时，轴压承载力提升了50.6%；当钢管壁厚从6 mm增加到10 mm时，轴压承载力升高了16.3%；当钢材强度从Q235变化至Q390时，轴压承载力增大了24.5%。当UHPC-CA强度由C130增强至C150时，轴压承载力仅降低了1.5 kN；由C150增强至C180时，轴压承载力升高了10.5%；C180 UHPC-CA对应的轴压承载力较C130 UHPC-CA增加了10.4%。可见，钢管外径、钢材强度和钢管壁厚的增加对短柱轴压承载力的增强作用较UHPC-CA强度更为显著，以上分析结果与极差分析结果相符合。限于本研究中的试验数据较少，圆钢管UHPC-CA短柱轴压承载力随各因素的变化情况需要进一步研究。

图2 轴压承载力随因素水平的变化

2.5 承载力-套箍系数分析

由以上分析可知，钢管外径对圆钢管UHPC-CA短柱轴压承载力的影响最大，图3示出了不同钢管外径条件下轴压承载力随套箍系数的变化情况。由图可知，当钢管外径为102 mm，套箍系数ξ由0.77增加至1.74时，轴压承载力升高了83.8%；钢管外径为121、133 mm时，轴压承载力分别提升了15.6%(ξ由0.65增加至1.44)和12.0%(ξ由0.57增加至1.50)。这是因为套箍系数ξ愈大，圆钢管对UHPC-CA的侧向约束效应愈强，最大主压应力轴的抗压强度与压缩变形能力提高得愈多[15]。可以看出，套箍系数增量相差不多时(0.79～0.97)，随着钢管外径的增加，圆钢管UHPC-CA短柱轴压承载力的增长幅度是逐渐降低的。

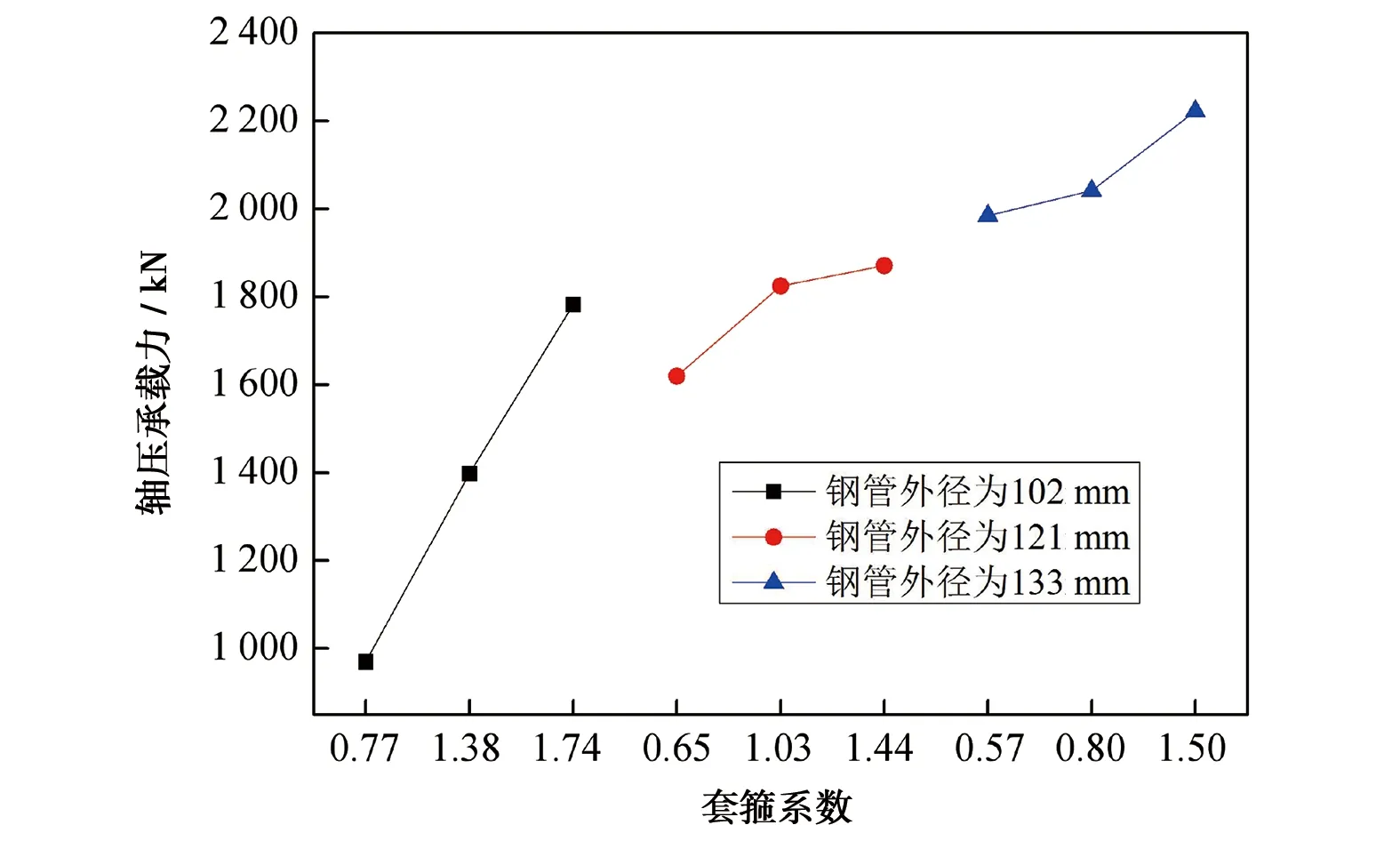
图3 轴压承载力随套箍系数的变化

2.6 承载力-径厚比分析

由层次分析可知，D1(C130UHPC-CA)和D2(C150UHPC-CA)对轴压承载力的影响权重值相同，均为0.037 7；由因素指标分析可知，当UHPC-CA强度由C130增强至C150时，轴压承载力仅降低了1.5 kN，变化不大。若忽略因素D水平1、2的不同影响，可得到不同钢材强度条件下圆钢管UHPC-CA短柱轴压承载力随径厚比的变化情况见图4。

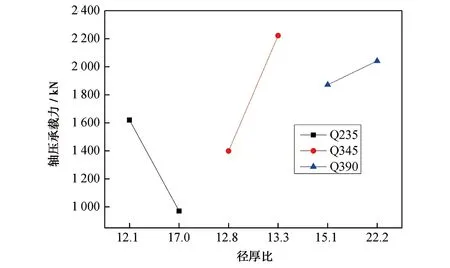
图4 轴压承载力随径厚比的变化

由图4可知，对于Q235钢系列柱，当径厚比从12.1增加至17.0时，圆钢管UHPC-CA短柱的轴压承载力降低40.1%；对于Q345钢系列柱，当径厚比从12.8增加至13.3时，轴压承载力升高30.5%；对于Q390钢系列柱，当径厚比由15.1增加至22.2时，轴压承载力提升9.1%。可见，不同钢材强度的圆钢管UHPC-CA短柱轴压承载力随径厚比的变化规律差异较大。