基于非广延小波特征尺度熵和支持向量机的轴承状态识别

董绍江，汤宝平，张 焱

(重庆大学 机械传动国家重点实验室，重庆 400030)

轴承作为机械设备的基础零部件，其安全运行对于机械设备的可靠性和安全性起到关键的作用。通过对轴承运行状态的准确识别和判定以便评估和预测轴承的寿命，对预防设备性能的进一步退化和失效意义重大。轴承状态识别的关键是振动信号的特征提取和状态的分类。经验模式分解(Empirical Mode Decomposition EMD)［1］，小波变换［2］等非线性分析方法能够在时频域对信号进行多尺度变换，具有多分辨率分析的特点，因此被广泛的应用于特征信息的提取。然而，实际采集到的振动信号往往噪声成分复杂、数据相关性强，因此，单纯依靠EMD，小波分解的方法提取信号的特征运算量较大，状态特征信息相对不明显。文献［2］将Shannon熵和小波分析相结合，特征提取的效果明显改善。但是Shannon熵属于B－G广延熵，而实验证明某些小波分解系数具有非广延性，即小波分解的过程中相邻尺度间可能存在能量泄漏和混叠［3］，因此用Shannon小波熵进行分析并不能准确的表征某些信号的特征，而非广延Tsallis熵克服了这一缺点［4］。因此本文选择Tsallis熵提取信号的特征。但是通过Tsallis熵分析后获得的特征信息仍存在维数较高，特征信息间冗余严重，敏感特征信息需要人为选取等问题，若选择不当将会严重影响轴承状态的判定。流形学分析算法LPP［5］是专门用于解决冗余信息严重情况下数据维数约简的新方法，克服了线性降维算法PCA，LDA不能处理非线性问题的困难，同时由于其通过寻找流形上的Laplace Beltrami算子的最优线性逼近特征函数，因此，相对ISOMAP，LE和LLE等非线性算法具有更高的处理速度。

轴承状态识别的另外一个重要步骤是在特征提取的基础上建立可靠的状态识别模型。文献［6］利用支持向量机建立了滚动轴承的状态寿命评估模型，并对滚动轴承的状态寿命进行了判定。虽然SVM具有较好的识别和分类的能力，但是标准的SVM存在对非线性特征信息不敏感，只适合均匀分布的样本并可能收敛于局部极值等问题［7］。文献［8－9］中提出的Morlet小波核向量机有效的解决了以上的问题，明显提高了向量机的识别精度和逼近精度。因此，本文将其作为轴承状态的识别模型。

根据以上的讨论，本文将非广延小波特征尺度熵和Morlet小波核支持向量机结合，提出了一种轴承状态判别的新方法，该方法充分发挥了非广延小波特征尺度熵在特征提取，流形学分析算法在数据维数约简和Morlet小波核支持向量机在模式识别方面的各自的优势，具有较高的识别精度。

1 非广延小波特征尺度熵

1.1 Shannon小波特征尺度熵存在的问题

Shannon小波特征尺度熵是小波分析和Shannon熵理论结合的产物，即对小波分解后不同尺度上的小波系数(或重构信号)进行 Shannon熵运算。但是Shannon熵属于广延熵，即Shannon小波特征尺度熵为小波分解重构后各尺度单支信号Shannon熵之和。但是，小波变换过程中存在着小波混叠和能量的泄漏等问题，造成利用Shannon熵对其计算并不合理，因为信号x(n)经过小波分解时，运算的主要算法是Mallat算法，被测信号经过m层小波分解后，低频和高频子带Dj(k)及 Aj(k)的频带范围为［3］:

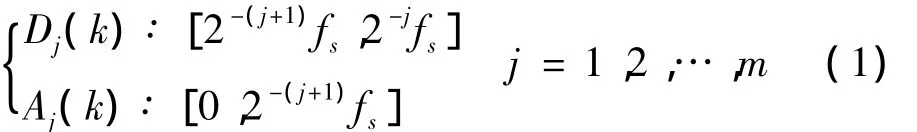
式中:fs为信号的采样频率。得到各个尺度下的小波系数:Dj={dj(k)，k=1，…，N，j=1，2，…，m}和尺度系数Am。但是从式(1)可以发现，随着分解层数的增大，在高频范围内由于信号间的相互影响，以及Mallat算法对高频段信号分解过于粗略，将造成相近的高频分量处于同一尺度。从而对熵值的准确性造成影响。

1.2 非广延Tsallis熵

Tsallis熵是统计物理学的一种新的信息度量方法，这种新的方法可以对混杂或是具有不规则的碎片形状的非可加性系统提供满意的物理解释。表达式为［10］:

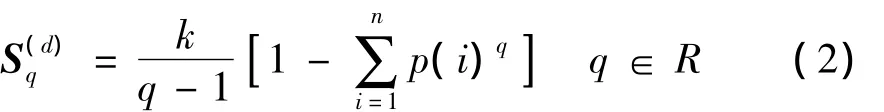
式中:q为非广延参数，p(i)为随机变量i的概率密度分布函数，k为常数，本文取k=1，

1.3 非广延小波特征尺度熵

在小波分解的基础上，对小波系数(或重构信号)定义一个滑动数据窗，设窗宽为 w∈N，滑动因子δ∈N，则滑动数据窗可以表示为:

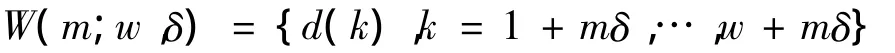
式中 m=1，2，…，(N －w)/δ。在尺度 j下的小波系数(或是重构信号)上滑动数据窗，将数据窗划分为L个=区间，有 ，其中{Zl［sl－1，sl］，l=1，2，…，L}，设pm(l)表示数据窗内小波系数(或重构信号)d(k)落入区间Zl的概率，则在第j尺度下Tsallis小波特征尺度熵定义为:

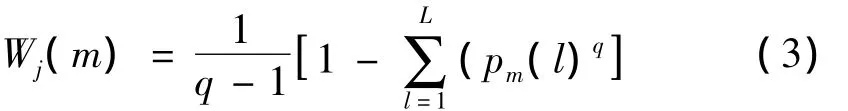
2 流形学习

流形学习的目标是发现嵌入在高维数据空间中的低维流形结构，并给出一个有效的低维表示。它能够较好地解决数据处理中的“维数灾难”问题。尤其是最近提出的流形学习算法LPP能够较好地发现数据空间中的局部几何结构，并具有计算简单的优点，因此，采用基于LPP的降维方法进行维数的处理是一种理想的选择。具体的算法描述见文献［5］。由于LPP是通过寻找优化线形映射来发现嵌入在高维数据空间的低维流形结构，并且是基于局部邻域结构的，因此嵌入向量的求解是求解稀疏矩阵的特征向量，从而大大减少了计算量，具有较高的运行速度。

3 Morlet小波核向量机模型的建立

支持向量机通过核函数实现函数的映射，核函数的选取将直接影响分类的精度。支持向量机的核函数必须满足的条件是 Mercer［11］定理。

定理1 L2(R)下的对称函数k(x，x')为特征空间中内积的充分必要条件是:对于使得的所有g≠0，如下条件成立:

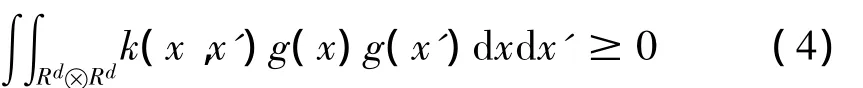
该定理提供了判断和构建核函数的方法。但是对于平移不变核函数，很难将其分解为两个相同函数的点积形式，因此由以下定理给出平移不变核函数的充分别要条件。

定理2 平移不变核函数k(x，x')=k(x－x')是一个允许支持向量机核，当且仅当其傅里叶变换满足:

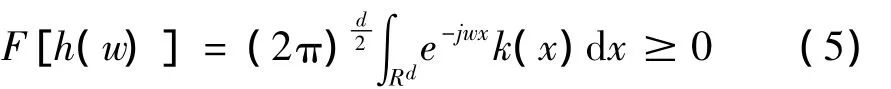
若小波函数ψ(x)满足ψ(x)∈L2(R)∩L1(R)，L1(R)为一次可积空间，且ψ(0)=0，则按照如下方式生成函数簇ψa，m(x)是连续小波:

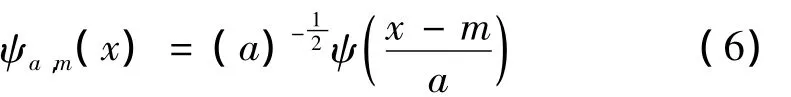
式中:m∈R;a≥0;a，m分别为伸缩和平移尺度因子;ψ(x)为母小波。利用Mercer定理和张量机理论［12］，若一维母小波函数为ψ(x)，可分离的d维小波函数的特殊情况可以写成:

根据上式，构造如下平移不变核函数:

其中ai＞0为小波收缩因子，平移不变核函数应严格满足定理2的允许条件。Morlet小波是满足该条件的小波，其表达式为:

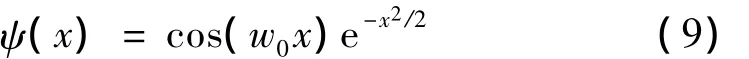
则基于Morlet小波构造的平移不变核函数为:

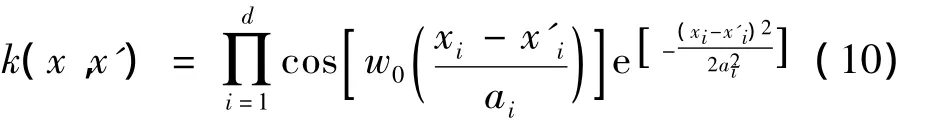
根据Mercer定理2的要求，将式(10)代入式(5)中得F［h(w)］≥0保证了核函数选择的正确性。

从而得到 Morlet小波核 SVM分类问题的输出函数:

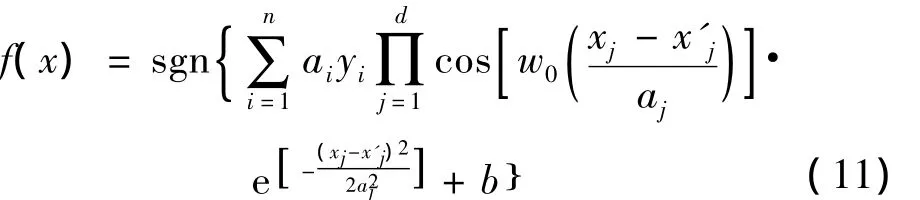
文中w0=5［8］，为了计算简便，将 aj=a即核函数参数个数变为了1，取a=0.3。

状态识别是个多分类问题，而支持向量机是个两类分类器，因此，应该将其构造为多类分类器，构造的思想是通过组合多个两类分类器进行，本文选择基于一对一算法［11］实现Morlet小波核多类SVM状态识别。

4 基于非广延小波特征尺度熵和Morlet小波核的轴承状态的识别

本文的基本思路是基于非广延小波特征尺度熵提取信号的特征信息并利用MWSVM进行状态识别，但是振动信号经过小波熵值进行特征提取后大量的熵特征信息间存在着混叠严重，数据维数较高的问题，若将这些信息输入到MWSVM中进行模式识别，由于数据量较大，数据间存在严重的冗余，将造成识别困难，甚至严重影响识别精度。因此，引入流形学算法LPP进行维数的约简，LPP维数约简的主要特点是整个提取过程不需要人为干预，并能实现数据冗余信息的剔除。将约简后的特征信息输入到MWSVM中进行模式识别。其具体流程(图1)和步骤如下:

图1 状态识别模型的实现流程Fig.1 The realization process of the state recognition

(1)将轴承信号(正常状态和故障状态)进行离散小波变换，获得各个尺度的系数。本文选取db5小波进行5层分解，利用Tsallis熵提取出各个尺度下的特征熵值，并将其进行归一化处理。

(2)利用流形学分析算法LPP对所提取的熵值进行维数约简。

(3)将约简后的特征数据输入到MWSVM中构建轴承状态的识别模型。

(4)将轴承实测数据进行步骤(1～2)的处理，将处理后的信号输入到识别模型中进行状态的识别。

5 试验分析

为了验证所提方法的有效性和实用性，对轴承正常情况下和几种故障状态下的数据进行分析。数据来自美国 Case Western Reserve University［13］。实验采用6205－2RS型深沟球轴承，轴承的内径为25mm，外径为52mm，厚度为15mm。滚动轴承实验装置由功率为1.5 kW的电动机、扭矩传感器/译码器、测力计和电器控制装置组成，由电机带动输入轴.模拟轴承在正常状态，内圈存在故障深度为0.18mm，0.36mm，0.53mm，0.71mm的情况下的运行状态，这样，数据就反映了轴承在运行状态不断恶化的情况下的运行情况。采样频率为12 kHz，选取1024个采样数据点进行分析。选取20， 15 ，外的5组用于测试。图2为一组轴承内圈正常状态和4种不同故障深度状态下的振动信号。

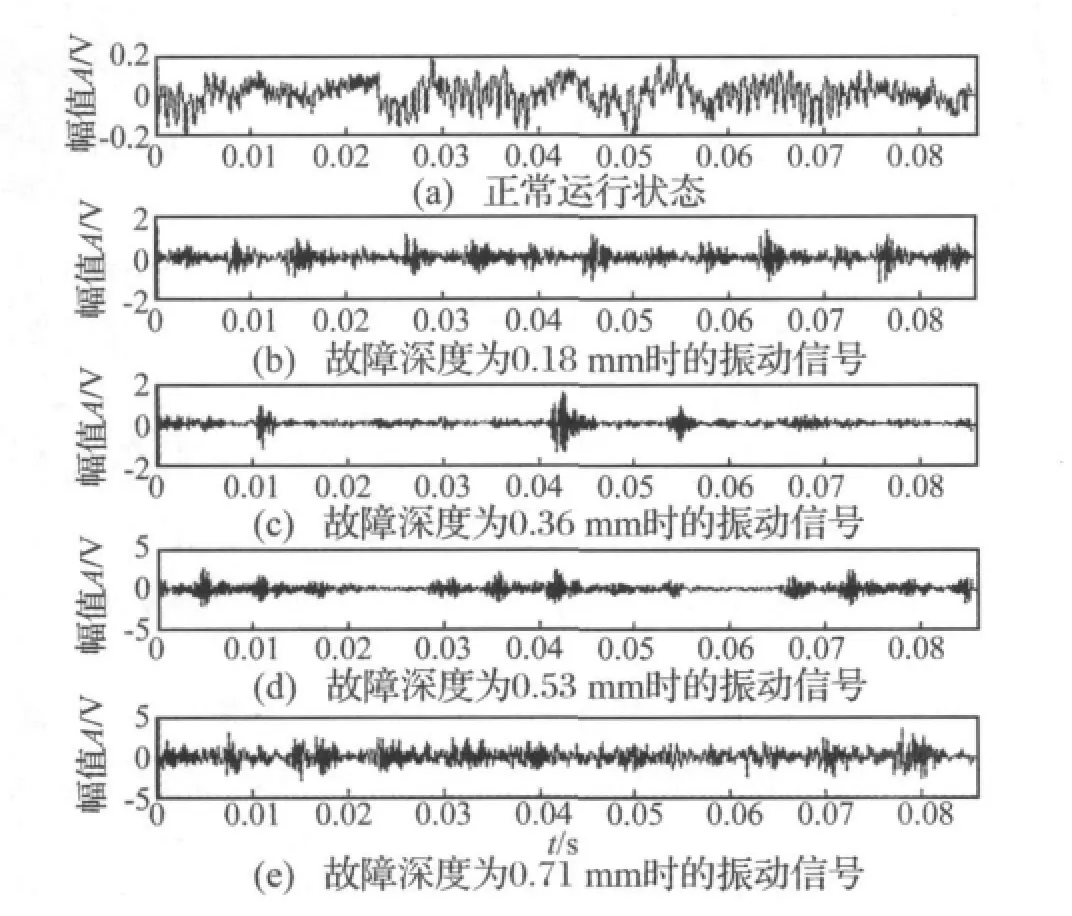
图2 一组内圈在不同运行状态下的振动信号Fig.2 A group of an inner race vibration signals under different operating conditions

对各组数据进行小波分解，并利用Tsallis熵提取特征信息，(由于第5层的低频重构信号熵值较小，因此，没有将其计入)。其中窗宽w设置为10，滑动因子δ设置为1，非广延参数 q取1.5［4］。获得的图2所示一组内圈信号的熵值如表1所示(未进行归一化处理前)。

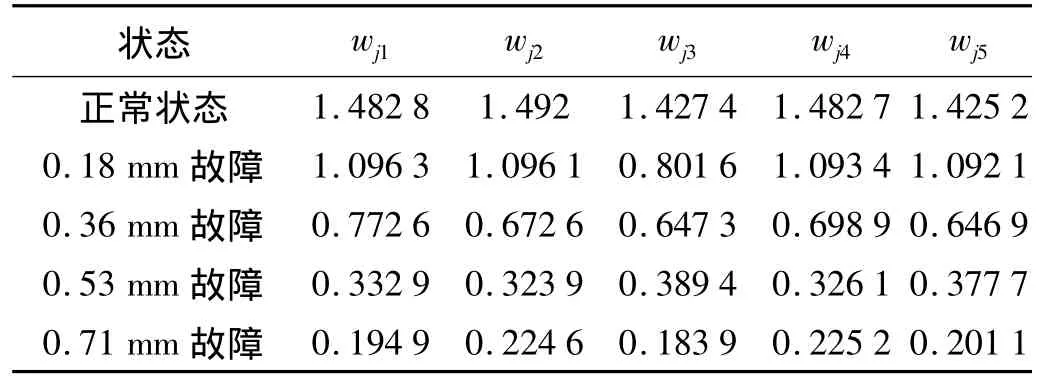
表1 轴承内圈5种运行状态下的非广延熵值Tab.1 The non-extensive wavelet feature scale entropy of inner race signal under five operating condiction

从表1可以看出，正常状态下的非广延小波熵值最大，因为在正常状态下，振动信号的能量分布相对平均，不确定因素较多。另外不同运行状态下振动信号的熵值也不相同，通过非广延小波特征尺度熵值可以粗略的反映轴承的状态。

将获得的15组数据的熵值进行归一化处理，并输入到LPP算法中进行维数的约简。约简后的效果图如图3所示，为了表明所选的LPP流形算法对维数的约简和冗余信息的处理效果，将LPP算法与局部线性嵌入算法(Locally Linear Embedding，LLE)对试验数据处理的效果(图4所示)进行对比:其中，为了具有可比性，将LPP和LLE维数设置为d=3，即输入MWSVM的数据维数为3，邻域数k=12。

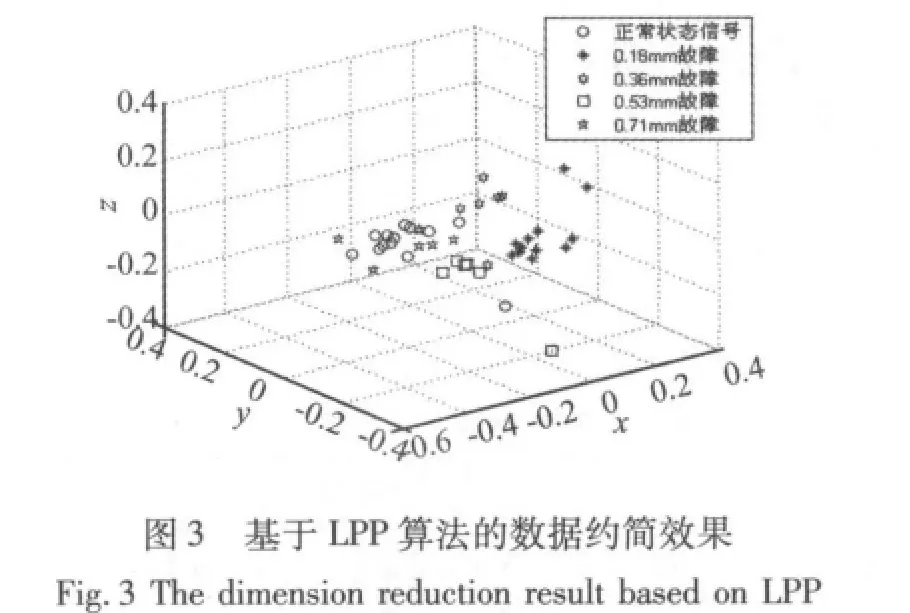
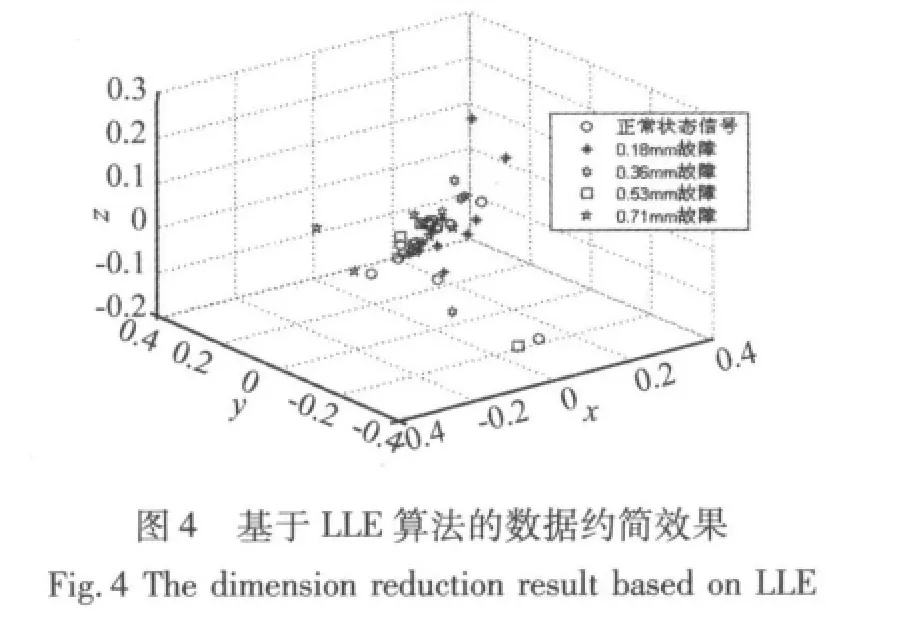
通过图3和图4对比发现，基于LPP约简后的数据被均匀的分开，达到了非线性数据降维和处理的目的。而基于LLE算法处理后，数据间仍存在严重混叠，将影响支持向量机的识别效果和精度。

将维数约简后的数据输入到支持向量机进行模型的训练和状态的识别，为了对比识别的效果，将:

(1)小波特征尺度熵处理后的数据不经过LPP约简直接输入到MWSVM;

(2)小波特征尺度熵处理后的数据通过LLE约简后输入到MWSVM;

(3)本文所提方法。进行对比，效果如表2所示。

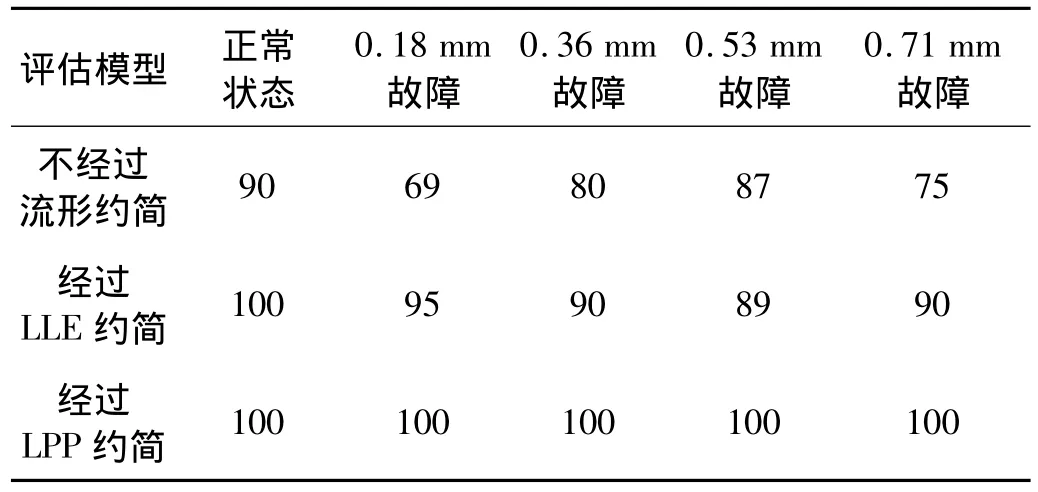
表2 3种识别方法的识别率对比分析 (识别率η%)Tab.2 The recognition rate of the three different methods

从表2可以看出，经过流形学LPP算法维数约简和敏感特征信息提取后，由于LPP对于空间局部几何结构的敏感性，从而状态识别精度明显提高，远高于其它两种算法的识别精度，因此，对熵值处理后的特征信息进行流形学LPP算法约简是有效的和实用的。

为了进一步验证所提方法的识别精度，将经过LPP约简后的特征信息输入普通的RBF(其中，惩罚因子C取100，核参数 γ=0.1)支持向量机和本文所提的MWSVM进行识别精度的对比，对比结果如表3所示。

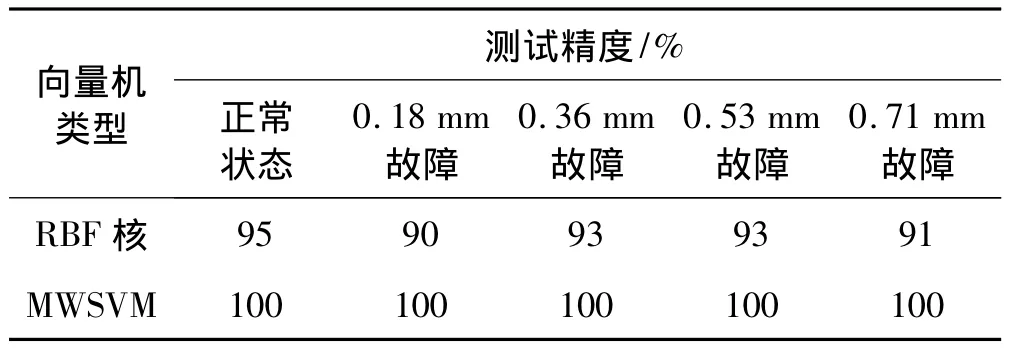
表3 RBF核和Morlet小波核支持向量机识别率比较Tab.3 The recognition rate between RBF and Morlet kernal SVM

通过表3的对比可以看出，基于Morlet小波核的支持向量机由于核函数对于敏感信息能够较好的识别和逼近，从而使得MWSVM的识别效果较普通RBF核支持向量机的识别效果明显较好，因此，选用MWSVM作为轴承状态的判别可以有效的提高识别的精度。

下面对比:①熵值信息不经过LPP约简直接用MWSVM进行识别的方法;②LPP约简后进行RBF向量机识别的方法;③本文方法，3种方法的训练和测试运行时间，对比结果如表4所示。

表4 3种方法的运行时间对比Tab.4 The running time comparison of three methods

从表4可以看出，经过维数约简后，向量机的识别速度明显提高，另外基于MWSVM的识别方法运行时间最短，原因在于Morlet小波核对冲击信息比较敏感，从而能够更加高效的处理数据信息。

6 结论

(1)分析了传统的Shannon小波熵所存在的问题，并提出了基于非广延小波特征尺度熵的特征提取方法，从而能更好的从轴承振动信号背景噪声中提取出轴承状态的信息。

(2)针对非广延小波特征尺度熵数据处理后熵值间维数较高，数据间冗余性较为严重的问题，为了有效地进行维数的约简，提取敏感的信息特征，减少约简过程中人为因素的干扰，本文通过流形学算法LPP进行特征维数的约简。

(3)为了更加精确地识别轴承的状态信息，选用Morlet小波核函数构造支持向量机，利用Morlet小波的信号逼近性来实现向量机识别精度的提高。

(4)通过对比分析，表明本文所提方法各个环节之间相互补充，充分发挥了各个部分的优势，从而实现了较好的识别精度和效率。

(5)实际的轴承运行过程中将存在几种状态混叠的情况，识别难度将更大。由于试验条件的限制，本文未予以讨论，但这是笔者将进一步深入研究的内容。

［1］张 超，陈建军，郭 迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法［J］.振动与冲击，2010，29(10):216－220.

［2］何正友，陈小勤.基于多尺度能量统计和小波能量熵测度的电力暂态信号识别方法［J］.中国电机工程学报，2006，26(10):33 －39.

［3］杨建国.小波分析及其工程应用［M］.北京:机械工业出版社，2005.

［4］陈继开，李浩昱，杨世彦，等.Tsallis小波包奇异熵与功率谱分析在电力谐波检测的应用［J］.电工技术学报，2010，25(8):193 －199.

［5］王自强，钱 旭.基于流形学习和SVM的Web文档分类算法［J］.计算机工程，2009，35(15):38－40.

［6］苗学问，田喜明，洪 杰.基于支持向量机的滚动轴承状态寿命模型［J］.航空动力学报，2008，23(12):2190－2195.

［7］汤宝平，李 锋，陈仁祥.基于Littlewood-Paley小波支持向量机的故障诊断［J］.振动与冲击，2011，30(1):128－131.

［8］武方方，赵银亮.一种基于Morlet小波核的约简支持向量机［J］.控制与决策，2006，21(8):848－856.

［9］周建萍，郑应平，王志萍.基于Morlet小波核多类支持向量机的故障诊断［J］.华东电力，2008，36(8):76 －79.

［10］Tsallis C.Possible generalization of boltzmann-gibbs statistics［J］.Journal of Statistical Physics，1988，52(1 － 2):479－487.

［11］Cristianini N，Taylor J S.An introduction to support vector machines and other Kernel-based learning methods［M］.New York:Cambridge University Press，2000.

［12］王向红，朱昌明，毛汉领.基于核主成分分析及支持向量机的水轮机叶片裂纹源定位［J］.振动与冲击，2010，29(11):226－229.

［13］These data comes from Case Western Reserve University Bearing Data Center website［OL］.http://www.eecs.cwru.edu/laboratory/bearing.