两自由度轧机非线性扭振系统的振动特性及失稳研究

侯东晓，刘 彬，时培明，刘 飞，刘云静

(1.东北大学 秦皇岛分样自动化工程系，秦皇岛 066004;2.燕山大学 电气工程学院，秦皇岛 066004)

随着轧制速度和轧制强度的不断提高，轧机传动系统在轧制过程中时常出现扭振现象，导致轧制产品的表面质量变差，剧烈的扭振还可能造成断辊、断带等事故，严重威胁轧制生产的安全运行。

轧机传动系统的扭振问题一直为科研人员所关注。文献［1］研究了一类具有非线性摩擦阻尼的单自由度轧机扭振动力学模型，分析了摩擦系数对系统自激振动的影响。文献［2］针对一类具有非线性刚度的扭振系统进行了研究，采用多尺度法得到了系统振动时的解析近似解。文献［3］研究了具有间隙时轧机传动系统的动力学特性，并针对间隙带来的扭振问题提出了一些解决方法。轧机传动系统实际上是一个多非线性因素共同作用的动力学系统，多非线性因素的存在使得轧机的扭振行为变得更为复杂，因此研究多非线性因素的影响才能更真实反映出轧机传动系统的非线性扭振特性。

本文考虑轧机传动系统传动轴的非线性刚度以及轧辊受到的非线性摩擦阻尼作用，建立了轧机传动系统的两自由度非线性扭振动力学方程。通过坐标变换得到电机加载力矩作用下系统的等效非线性扭振方程。分析了该非线性扭振系统在周期激励下的主共振和分岔特性。最后以实际轧机为例，研究非线性参数对轧机主共振幅频特性的影响以及导致轧机出现失稳振动的条件，为保证轧机传动系统的稳定运行提供了理论参考。

1 具有非线性刚度和非线性摩擦阻尼的两自由轧机非线性扭振模型

在轧制状态下，考虑轧机传动系统传动轴的非线性刚度［4］以及轧辊与轧件间非线性摩擦阻尼［1，5］，可将轧机传动系统简化为由电机和负载组成的两自由度非线性扭振力学模型(如图1所示)。

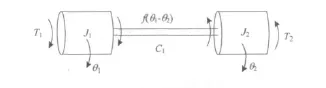
图1 两自由度轧机非线性扭振力学模型Fig.1 The 2 DOF nonlinear mechanical model of torsional vibration of rolling mill

图中J1和J2分别为电机和负载的等效转动惯量，θ1与θ2分别为电机和负载运转时的扭转角，f(θ1-θ2)=K1(θ1-θ2)+K2(θ1-θ2)3为轧机传动轴的非线性刚度，C为传动轴的结构阻尼系数，T1为电机输入力矩，T2为负载端受到的非线性摩擦阻尼，T2=-aRPe-bRθ·2+c，其中P为轧制力，R为轧辊半径。

由图1中力学模型可得到如下两自由度非线性扭振方程:

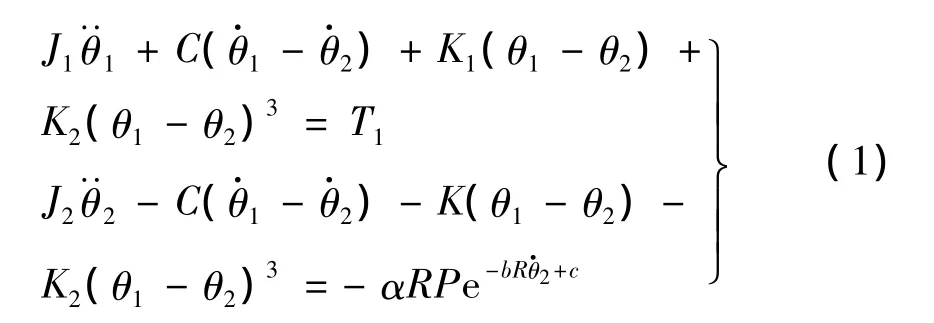
2 电机加载力矩下等效非线性扭振方程

轧机传动系统运转时的转动角是随时间变化的，由于非线性因素的影响，轧机传动系统在零点附近的运行和稳定状态［2，4］将与传动系统受电机加载力矩作用时实际运行情况有较大差别［6］，研究电机加载力矩作用下的轧机传动系统更接近于实际。

令电机加载力矩T1=T'1+T″1，其中T'1为电机加载力矩的恒定成分，为一常量，T″1为电机加载力矩的扰动成分。此时电机和负载端的相对扭转角可写为θ1-θ2=Δθ+x1-x2，其中 Δθ为恒定加载力矩T'1造成的扭转角，为一常量，x1和x2为扰动力矩T″1造成的扭转波动角;电机和负载的转动速度可分别表示为，其中和分别为由力矩T'1形成的电机和负载的稳定转速，存在;电机和负载的转动加速度可分别表示为，在恒定力矩T'1下存在。将上述的代入式(1)中，并将负载端的非线性摩擦阻尼在稳定转速处泰勒公式展开，可得到轧机传动系统在稳定点附近的等效非线性扭振方程:

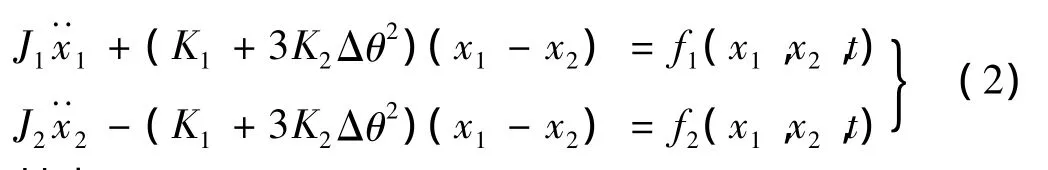
其中:

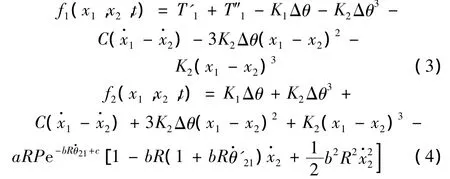
在上述非线性扭振方程中，当系统的扰动力矩趋于0时，即T″1=0时，存在如下的平衡力:

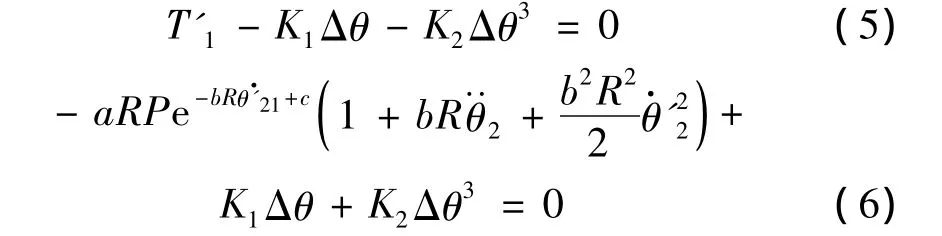
其中，Δθ和θ·21为恒定加载力矩形成的传动轴扭转角和负载端转速，为轧机传动系统运行时的稳定点。

将式(5)、式(6)代入式(2)中，考虑到式(2)中的非线性项为弱非线性，将其冠以小参数ε，可得到如下矩阵形式:

其中:

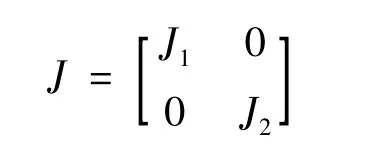
为系统的惯量矩阵;

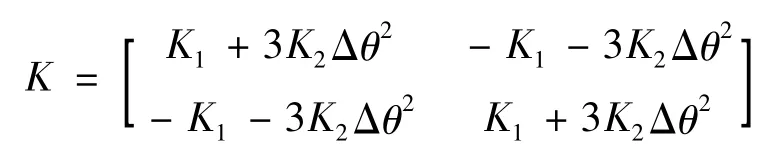
为系统的刚度矩阵;

f(x1，x2，t)=［f'1(x1，x2，t)f'2(x1，x2，t)］T为系统的非线性作用力矩阵，此时:

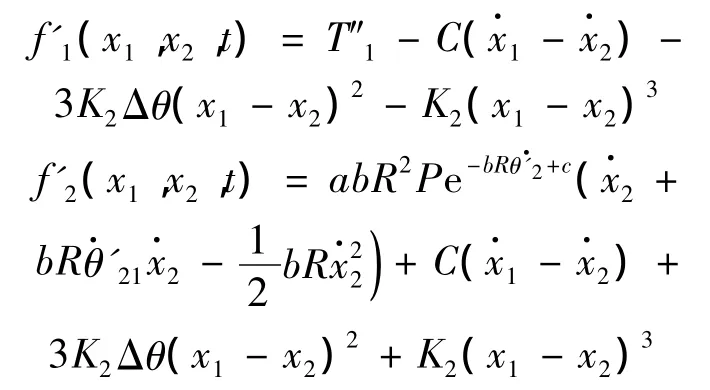
由上可见，在电机加载力矩作用下，轧机传动系统的非线性扭振方程转换为一个同时包含二次及三次非线性项的方程。

3 非线性扭振系统的振动特性分析

3.1 非线性扭振系统的主共振特性分析

由于式(7)中的两自由度非线性扭振方程只存在一个固有频率，因此可只考虑单频振动作用影响，即认为该系统是以系统的固有频率或某一种频率为主的振动［7］。

当轧机传动系统受到外部周期激励扰动频率ω接近于系统的固有频率ω0时，即T″1=F0sin(ωt)，采用平均法设式(7)存在如下形式的周期解:

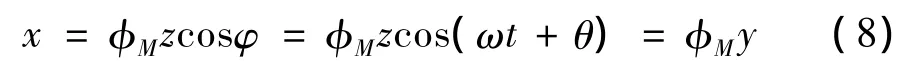
式(8)中的φM=［φM1φM2］T为振型函数，可通过求解式(7)的奇次方程组得到，该奇次方程组如下:

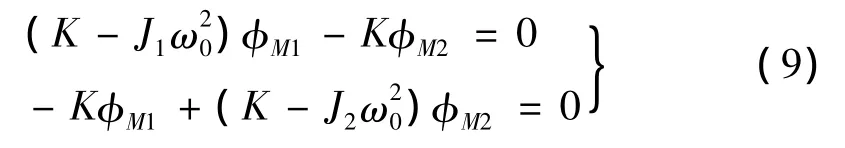
式(9)中ω0为系统的固有频率，可通过求解如下特征行列式得到:

由式(10)可解得:

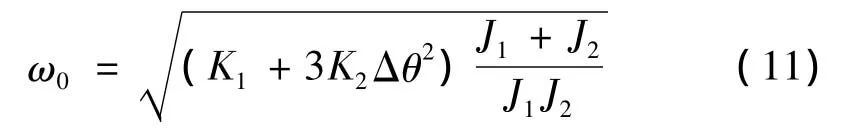
将式(11)代入式(9)可解得:

将式(7)的左边和右边都乘以φTM，可将式(7)化为第一主坐标上的方程式:

其中主质量M1和主刚度M1ω20分别为:

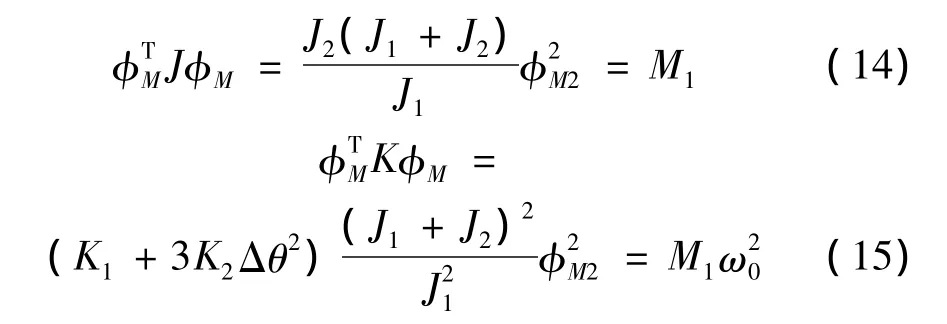
式(13)右边的非线性项为:

其中:

由于式(13)的方程在主坐标上是独立的，因此可采用单自由度系统的求解方法对系统进行分析。

考虑到轧机传动系统受到的扰动频率ω接近系统固有频率ω0，设:

其中σ为调谐因子。

将式(17)代入式(13)可得:

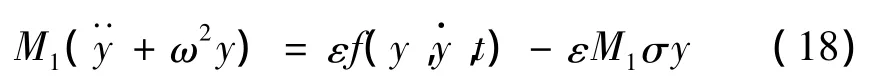
采用平均法可得到系统的幅值和频率方程为:

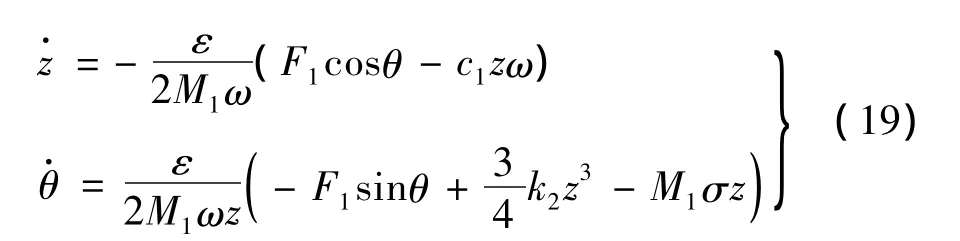
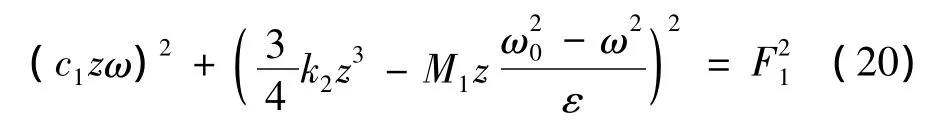
3.2 非线性扭振系统的分岔特性分析

为分析系统主共振时的分岔特性，可将式(20)考虑为奇异性理论中的一个开折问题，通过引进附加参数来研究扰动对方程分岔形态的影响。

将式(20)展开可得如下形式:

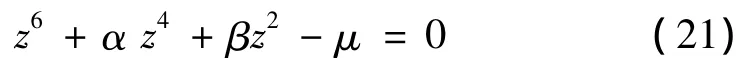
其中:

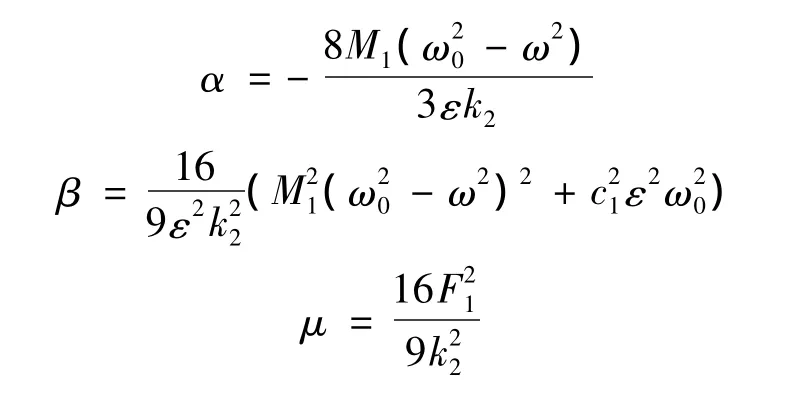
式(21)可写为:

将式(22)写成如下形式:

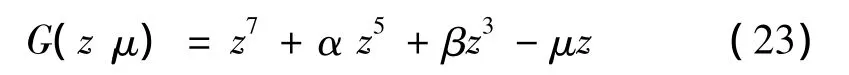
由奇异性理论可知，式(23)是范式z7-μz=0的普适开折，其余维数为2。其中，α、β为开折参数，其不同的取值会导致系统出现不同的分岔形式;μ为分岔参数，在确定的分岔形式下，振幅z将随系统的参数μ的变化而发生变化。

分别将式(23)对z和μ求导，可得到:

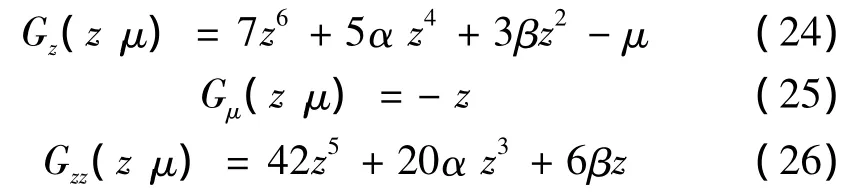
根据转迁集的定义可得:

(1)当G(z，μ)=Gz(z，μ)=Gμ(z，μ)=0 时，存在分岔点集B0(Z2)=φ，B1(Z2)=φ;

(2)当G(z，μ)=Gz(z，μ)=Gzz(z，μ)=0 时，存在滞后点集H0(Z2)={β=0}，H1(Z2)={β=α2/3，α≤0};

(3)存在双极限点集D(Z2)={β=α2/4，α≤0};

(4)系统的转迁集∑=B0∪B1∪H0∪H1∪D。

图2为系统在不同开折参数α和β下的转迁集。

图3为系统在不同的转迁集以及转迁集划分的区域中对应的分岔曲线。

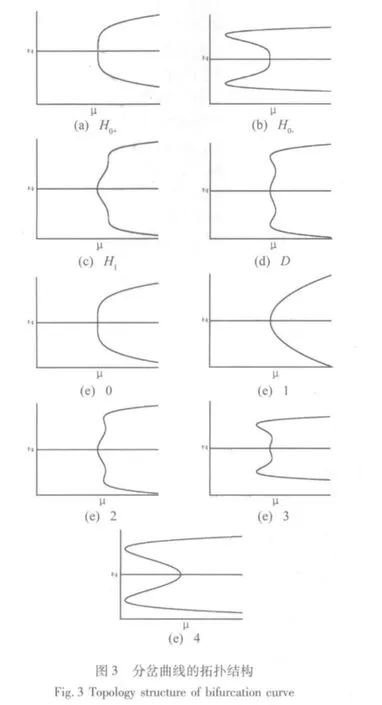
由图3可见，系统具有9种不同的分岔形式，其中，H1、H0+、H0-、D为系统转迁集上的分岔曲线，(e)1、(e)2、(e)3和(e)4为转迁集划分出的4个不同分岔区域，在这4个分岔区域中，(e)2、(e)3和(e)4都存在幅值跳跃现象，这对轧机的振动是不利的，因此应尽量使系统的开折参数保持在区域图3(e)1中。

4 仿真分析

以某厂1780轧机传动系统为例，取如下参数:J1=1.317 ×104kg·m2，J2=913 kg·m2，K1=1.13 × 107Nm/rad，C=1.6 × 104N/(m·s-1)，R=0.42 m，a=0.1，b=0.02，c=0.5，T'1=2.15 ×106Nm，P=3.14 ×107N，φM2=1。

由式(20)可得到在不同非线性参数影响下系统的幅频响应变化曲线。其中图4为不同非线性刚度下系统的幅频响应曲线，可见非线性刚度将使系统的幅频曲线发生弯曲，导致系统出现跳跃现象。

图5为取不同非线性阻尼时系统的幅频响应曲线。

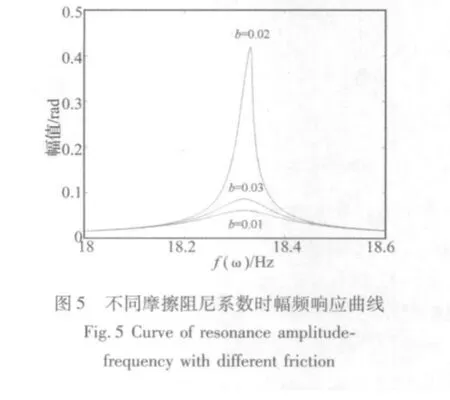
由图5可知，非线性阻尼系数的变化会影响系统共振的大小，阻尼系数b值对共振的影响比较复杂，当b在0.02附近时，系统的等效阻尼系数c1将最小，此时系统的共振将最大，当远离0.02时，c1增大，正阻尼效应变强，共振幅值变小。

轧机阻尼系数的选取对传动系统的稳定性有着重要作用。当阻尼系数c1＞0时，轧机传动系统的阻尼为负，此时将产生负阻尼效应，导致轧机发生失稳振动。因此当轧机传动系统中阻尼系数c1＜0，即满足如下条件:

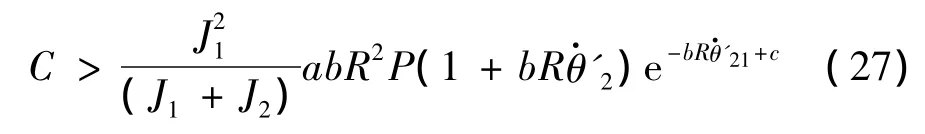
此时轧机传动系统是稳定的，否则系统将发生发散性振动。由式(27)可看出，传动系统电机和负载的转动惯量、轧辊半径、轧制力、轧制速度、摩擦系数以及结构阻尼系数都会影响轧机运行的稳定性，轧制生产中应适当选取这些参数，才能避免轧机失稳振动的发生。

图6和图7为在不同的轧制速度下轧机出现振动的仿真曲线。其中图6为轧制速度等于61.6 rad/s时，c1=-6.26×103N/(m·s-1)＞0，此时轧机的振动是稳定的。

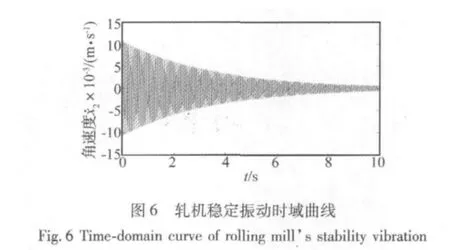
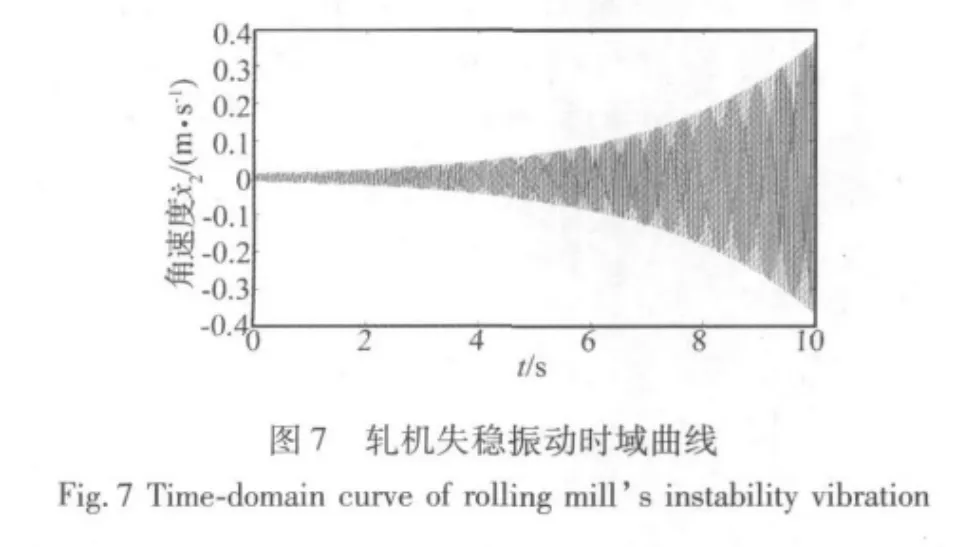
图7中轧制速度为6.6 rad/s时，c1=5.47×103N/(m·s-1)＞0，此时轧机将产生失稳振动，这与现场发生发散性振动是比较相似的［8］。由图7可看出，轧机发生振动时，系统的振动发散，振幅随时间增大，这将对轧制生产造成很大的影响，应尽量避免这类振动的发生。

由文中仿真可知，轧机失稳振动发生于轧制速度有着密切关系，这里应注意的是文中考虑的非线性摩擦阻尼只发生在轧制过程中某一速度段(即混合摩擦状态)［8］，因此对轧制工艺进行设计时，应尽量避免轧制速度的不稳定区域与混合摩擦状态下速度区域重合，这样可减少这一类不稳定振动的发生。

5 结论

(1)建立了具有非线线性摩擦阻尼的轧机传动系统两自由度非线性扭振动力学方程，并通过坐标变换得到电机加载力矩作用下轧机传动系统的等效非线性扭振方程。

(2)得到轧机在外部周期激励下的主共振分岔方程，应用奇异性理论得到系统的转迁集以及系统出现各种分岔行为的条件，并通过数值仿真分析了非线性刚度系数以及非线性阻尼系数对轧机主共振的影响。

(3)得到轧机发生失稳振动的条件，发现轧机传动系统中电机和负载的转动惯量、轧辊半径、轧制力、轧制速度、轧辊与轧件间摩擦系数以及结构阻尼系数等都会影响轧机运行的稳定性，生产中应适当选取这些参数，使其满足式(27)，才能避免轧机失稳振动的发生，这可为抑制轧机扭振和保证轧机平稳运行提供理论参考。

［1］鲁晓燕，叶黔元，瞿志豪.一类轧机自激振动现象的分析与解决［J］.上海理工大学学报，2004，26(2):141-144.

［2］时培明，刘 彬.相对转动非线性系统及其在强迫激励下的解［J］.物理学报，2007，56(7):3678-3682.

［3］ Wang Z H，Wang D J.Dynamic characteristics of a rolling mill drive system with backlash in rolling slippage［J］.Journal of Materials Processing Technology，2000，97(1):69-73.

［4］ El-Bassiouny A F.Vibration and chaos control of nonlinear torsional vibrating systems［J］.Physica A，2006，366(1):167-186.

［5］ Niziol J，Swiatoniowski A.Numerical analysis of the vertical vibrations of rolling mills and their negative effect on the sheet quality［J］.Journal of Materials Processing Technology，2005，162(15):546-550.

［6］刘浩然，张业宽，李晓梅，等.轧机非线性传动系统冲击扭振的研究与抑制［J］.振动与冲击，2010，29(7):179-183.

［7］郑兆昌.关于线性和非线性系统内在的本质联系——多自由度非线性系统的定性与定量分析［J］.振动与冲击，2008，21(1):4-8.

［8］邹家祥，徐乐江.冷连轧机系统振动控制［M］.北京:冶金工业出版社，1998:75-95.