大跨越高压输电线路覆冰断线的冲击动力学模型

刘春城，初佂宇，孙显鹤，张 伟

(1.东北电力大学 建筑工程学院，吉林省 吉林 132012;2.大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116023)

输电线路覆冰是一种严重的自然灾害，覆冰造成断线、倒杆(塔)事故时有发生［1］。1993年美国Nebraska州发生多米诺骨牌效应的连续倒塔事故，400多基输电杆塔发生连续倒塔［2］。2008年1月，我国南方电网大部分地区遭受了50年一遇的冰雪凝冻灾害，造成电网区域4 216条输电线路被破坏，线路破坏的主要形式为断线和倒塔［3］。大跨越输电塔-线体系作为高压电能输送的载体，由于档距、高差较大、铁塔高柔等特点，线路覆冰对其影响更加严重，同时，大跨越输电线路的电压等级较高，载流量较大，线路破坏造成的经济损失巨大。

线路断线的冲击荷载不但会引发线路振荡，同时也给本来承受较大覆冰荷载的输电杆塔带来巨大的冲击力和不平衡断线张力，当输电杆塔主要承重构件达到其极限承载力时，杆塔会发生局部压曲失稳倒塔。目前，我国的架空输电线路设计规范和标准［4，5］中对于覆冰的计算通常是按等效静力荷载方法来考虑的，对于线路的覆冰断线冲击效应并未涉及，可见，现有输电线路覆冰设计标准是偏低的。关于输电线路断线的研究可以追溯到20世纪七八十年代，Peyrot等［6］结合实测研究了输电线路断线动态张力前两个峰值的估算公式。Mozer和Wood William等［7］，通过对输电杆塔线体系进行模型试验，测试出了输电杆塔在断线情况下顺导线方向的静态和动态响应，Fleming 和 Siddiqui等［8，9］编制了通用程序计算当一根或多根导线突然断裂时输电杆塔线体系受到的动力冲击响应，Thomas等［10］提出了对于不同的导线配置基于数字方法的断线荷载历程。McClure和Rene tinawi［11］提出了断线一致响应的数学模型，McClure，Lapointe［12］曾使用 ADINA 程序来进行断线瞬态响应动力分析。在国内，李黎、沈国辉等［13-16］利用数值模拟技术研究了导(地)线突然断线的冲击响应和跌落过程的震荡效应。从以上研究来看，研究成果主要体现在利用数值方法研究输电线路断线响应，没有从理论上进行系统研究，同时没有考虑输电杆塔和导(地)线的覆冰断线的冲击影响。本文在已有研究基础上，针对大跨越输电线路、导线分裂布置的输电线路覆冰情况，基于能量方法，建立覆冰断线的冲击动力学模型，以某大跨越输电线路的一个典型耐张段为实例，给出了不同断线工况下的覆冰断线对塔线体系的冲击动力响应。

1 冲击动力学模型

1.1 运动模型描述

导(地)线覆冰断线分析通常按平面内的水平与竖直运动考虑，现场实际观测表明，分裂导线断线过程中由于覆冰的不均匀性，还常常发生扭转运动。本文以等效单根导线代替分裂导线，以导线整体运动为前提，将子导线的横截面中心用一根等效单导线的虚拟曲线即参考曲线连接起来，其运动与分裂导线的运动同步。将分裂导线视为柔性索，用间隔棒联结起来，组成一种柔性构件。导线的静态位置由其本身自重、覆冰重量、以及初张力确定。假设分裂导线的参照曲线中心与横截面质量中心重合，忽略偏心;此外，相邻档距均作理想化假定，导线约束用等效线性弹簧代替。等效单导线模型采用了间隔器和参照曲线，如图1所示。

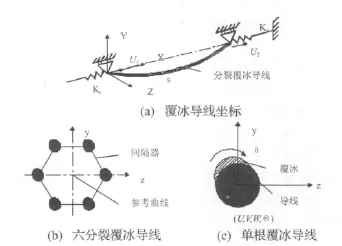
图1 导线覆冰模型Fig.1 Ice accretion model of wire

1.2 基本假定

为将单导线模型应用于分裂导线，引入如下假定:

(1)惯性力和阻尼力分布于线路纵向，忽略该方向各导线的旋转分量;

(2)导线的垂跨比很小;

(3)不考虑导线脱冰引起的冲击响应;

(4)忽略分裂导线间的相对运动，导线的纵向运动同步;

(5)耐张塔认为是刚性的，绝缘子和相邻档导线连接可认为是弹簧连接。

1.3 运动方程的建立

由图1可知，位移关系可描述为:

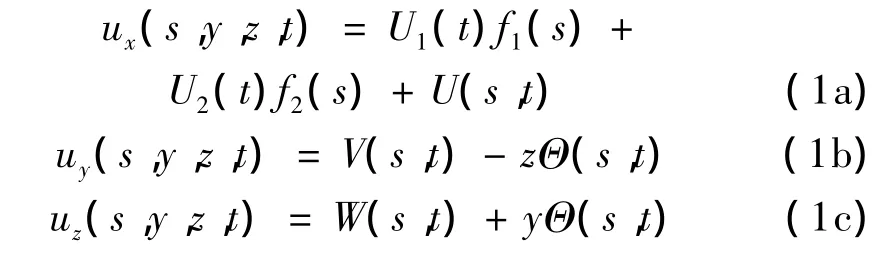
式中，X、Y、Z为总体坐标系，x、y、z为局部坐标系，ux、uy、uz为局部坐标系下t时刻在坐标点(s，y，z)处的位移，U(s，t)、V(s，t)、W(s，t)分别为参考曲线上任意一点在t时刻沿X、Y、Z方向的整体位移;U1(t)和U2(t)分别为导线左、右悬挂点在t时刻的位移，s为分裂导线横截面距参考曲线原点沿导线长度方向的坐标长度。f1(s)和f2(s)为参考曲线坐标s的函数，这里f1(s)=1-s/L，f2(s)=s/L，L为某一档距内导线的实际长度。Θ为分裂子导线相对于参考曲线的扭转角位移。

一般情况下，U(s，t)、V(s，t)、W(s，t)、Θ(s，t)可表示为如下形式:

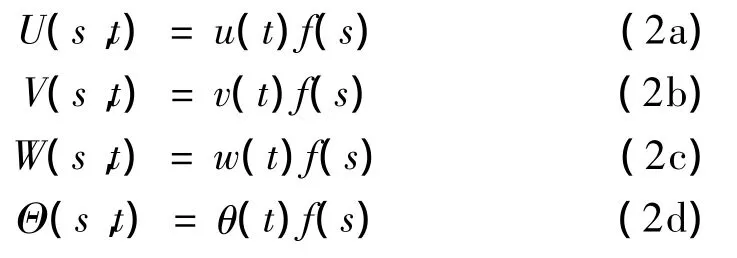
式中，u(t)，v(t)，w(t)，θ(t)为广义坐标，f(s)为相应的振型位移。

利用变分原理，运动方程的变分形式为:

式中，Tk和Ve分别为总的动能和势能;Wnc为非保守力所做的功;δ表示一阶变分。

由位移关系可知，各部分能量可表示为:

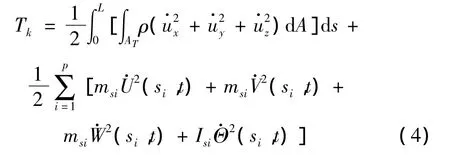
式中ρ为覆冰导线的等效密度，AT为等效单根覆冰导线的总截面面积，L为某一档距内导线的实际长度;msi和Isi分别为第i个间隔器质量和惯性矩;si为第i个间隔器沿参考曲线方向的固有坐标;p为间隔器的数量。

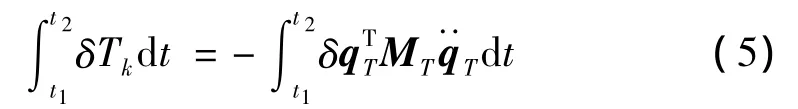
这里，

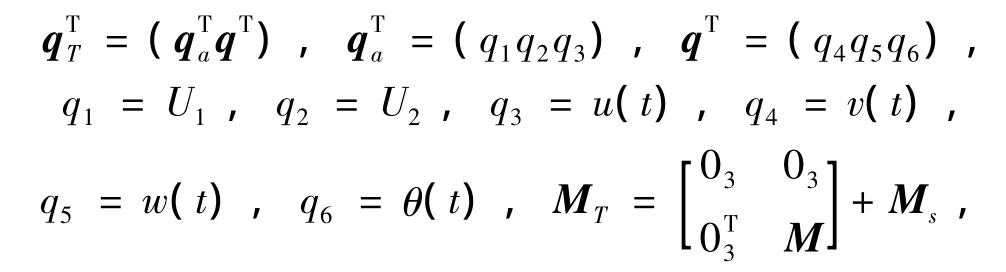
式中，03为3×3阶零矩阵，矩阵M的元素分别为mij=βijfi+3fj+3ds，i，j=1，2，3，且M为对称矩阵。其中β11=β22= ∫ATρdA，β33= ∫AT(y2+z2)ρdA，β13=- ∫ATzρdA，β23=∫ATyρdA，β12=β21=0，Ms为间隔器形成的质量矩阵，可表示为:

分裂导线整体运动的势能包括重力势能和应变能两部分之和，总势能公式可表示为:

式中ε，σ分别为应变、应力列向量，可表示为:

其中εs为沿参考曲线方向的拉格朗日应变，εθ为扭转角应变。

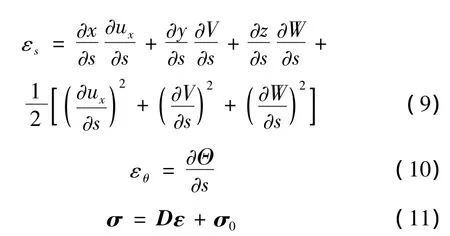
其中D为弹性矩阵，σ0为初应力矩阵。

式中A为等效单根导线的总截面面积，E为弹性模量，BT为轴向-扭转耦合刚度，GJ为单根导线抗扭刚度。

式中，T为单根导线初始静张力，M0为单根导线初始静扭矩。

式中，KT为6×6阶刚度矩阵。

由于非保守力只有阻尼力存在，则有:

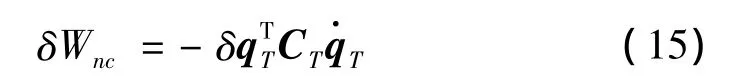
代人运动方程(3)，通过变分可得:

其中:

式中，03为3×3阶零矩阵，对角矩阵C的元素分别为:

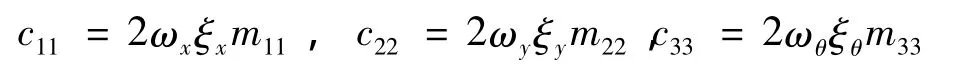
KT的元素分别为:

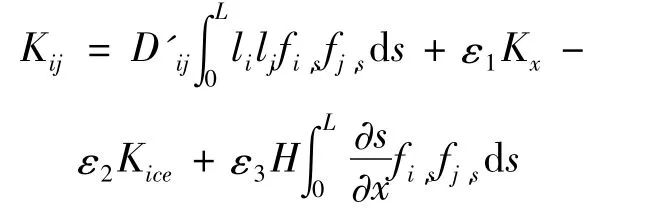
其中:

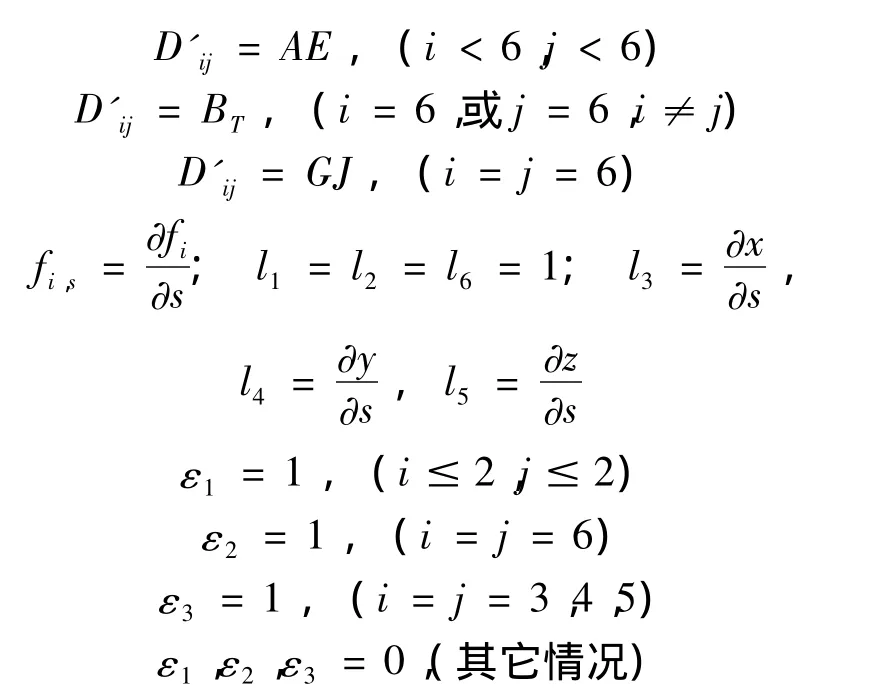
其中，Kx为导线耦合刚度，包括轴向抗拉刚度和导线与绝缘子及相邻档距耦合刚度之和，本文采用Veletsos和Darbre给出的计算公式［17］。Kice为导线覆冰刚度，本文采用 Gortemaker［18］给出的计算公式。

2 工程实例

本文选取某1 000 kV大跨越输电线路的一耐张段为研究对象，耐张段为耐-直-直-直-耐型式，档距为450 m+1 220 m+995 m+986 m。直线塔为钢管角钢混合酒杯型铁塔，耐张塔为干字型角钢塔。直线塔高122.8 m，耐张塔高68.0 m，导线为六分裂型式。耐张塔由于刚度很大，以固结方式简化处理。塔线体系纵断面图见图1。三塔四线体系从左到右依次设定为1#塔、2#塔和3#塔;档距从左到右依次为第一、第二、第三和第四档距;导线及地线断线点位于2#塔右侧，见图3。关于断线对输电塔作用的施加和计算，在本文中是采取瞬间在断点释放导线，让导线做自由落体运动，时间采取1e-8 s。由于塔头、横担端、曲臂、塔颈以及塔腿是工程实际中铁塔易损坏的部位，也是铁塔的主要控制截面，本文提取以上部位的内力和位移响应，控制截面位置见图4。

每基铁塔杆件上千根，为一个较复杂的格构式塔架。铁塔钢材分别为Q235、345和420等规格。钢材的弹性模量E=210 GPa，密度为ρ=7 850 kg/m3，泊松比为μ=0.3。导地线材料及参数见表1。

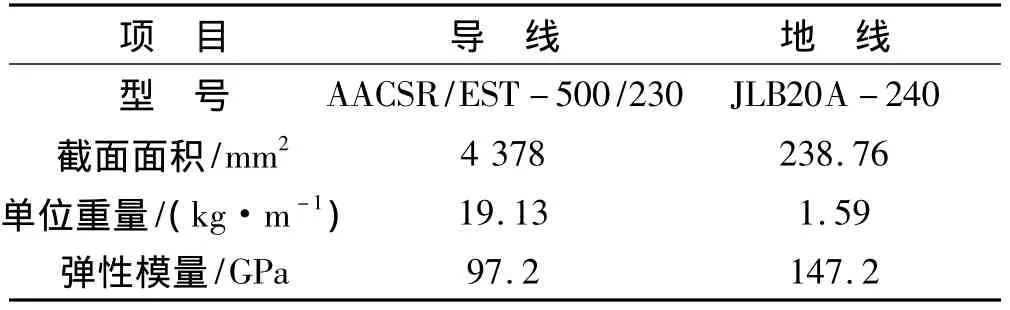
表1 导地线参数Tab.1 Conductor and ground wire's parameter

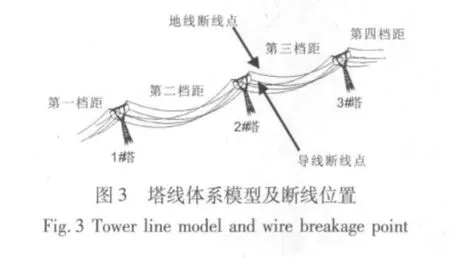
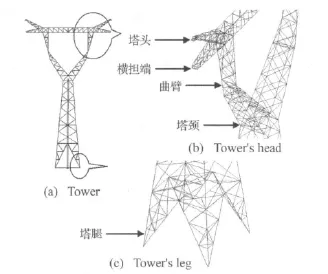
图4 直线塔及其控制截面位置Fig.4 Tower and its controlling section

3 导地线覆冰断线冲击响应计算

本文计算了在无风无冰以及无风10 mm覆冰两种工况下，断1相导线和1相地线时体系的动力响应。设分析时间为30 s，对于无冰工况，0-5 s为体系自重平衡阶段;对于有冰工况，0-5 s为体系覆冰平衡阶段;第5 s开始断线，断线时间极短，可以认为是瞬间断线;5 s以后为体系振荡阶段。

经分析可知，距断线点最近的2#塔所受的断线冲击响应最大，提取并对比了线路无覆冰和10 mm覆冰条件下2#输电杆塔各控制截面处的响应。

3.1 无冰断导线及10 mm覆冰断导线的体系响应

图5至图8为无覆冰及10 mm覆冰工况下，导线断裂时2号塔的塔腿、塔颈、横担端、塔头轴力响应。图10、图11为无覆冰及10 mm工况下，导线断裂时2#塔塔头、横担端处的位移响应。

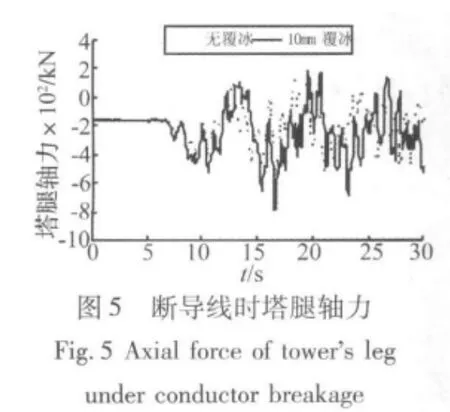
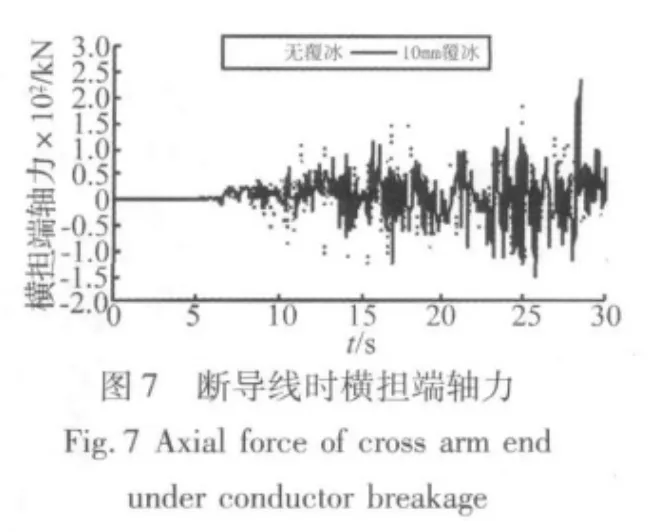
从图5至图8可以看出，在导地线覆冰条件下，覆冰断线产生的轴力皆大于无覆冰时导线断裂产生的轴力。由图可知，断线对塔腿和横担端的轴力冲击响应最大，对于横担端处:无覆冰时轴向拉力为194.493 kN，轴向压力为 -124.404 kN，轴力随时间波动的幅值为318.897 kN;10 mm覆冰断线时轴向拉力为 236.600 kN，增 大 21.65%，轴 向 压 力 为-151.973 kN，增大27.57%，轴力随时间波动的幅值为388.473 kN。对于塔腿处:由图可见，无冰断线时的轴力幅值为645.26 kN，而覆冰断线情况下轴力幅值可达 780.93 kN，增加21.03%，由此可见，10 mm 覆冰后断导线对铁塔轴力的冲击增大很多。图9和图10给出了无冰和10 mm覆冰断导线工况下，2#塔塔头和横担端位移时程曲线，由两图可见，断线后塔头摆动位移最大，无冰断线时塔顶位移的最大幅值为588.6 mm，而位移随时间波动幅度可达916.2 mm;10 mm覆冰断线时位移最大幅值为873.8 mm，位移随时间波动幅度可达1 290.3 mm。分别增大了48.45%和40.83%，因此覆冰断线对铁塔的位移冲击响应也显著增大。

3.2 无冰断地线及10 mm覆冰断地线响应

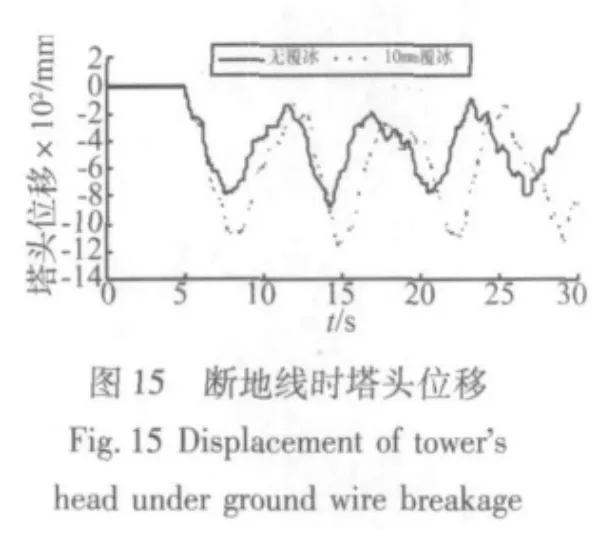
图11至图13为无覆冰及10 mm覆冰工况下，地线断裂时2#塔塔腿、曲臂、横担端轴力响应。图14给出了无冰工况断导线和断地线的响应。图15、图16给出了无覆冰及10 mm工况下，地线断裂时2#塔塔头、曲臂位移响应。

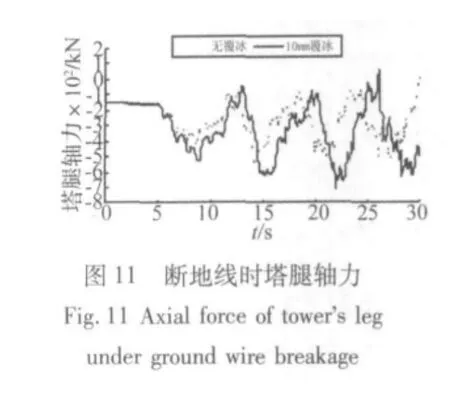
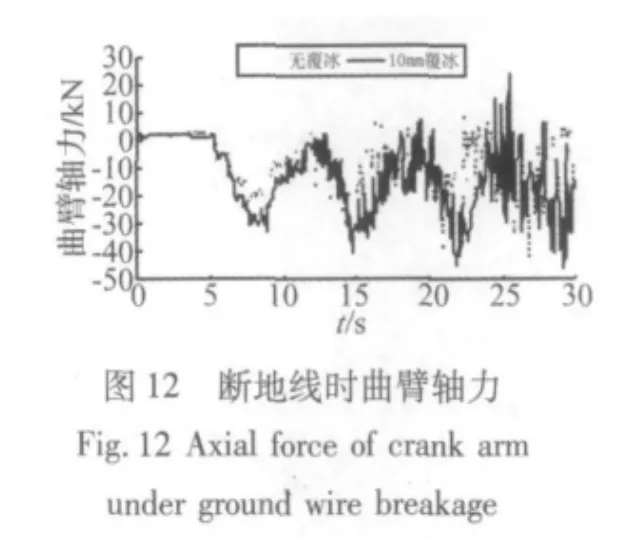
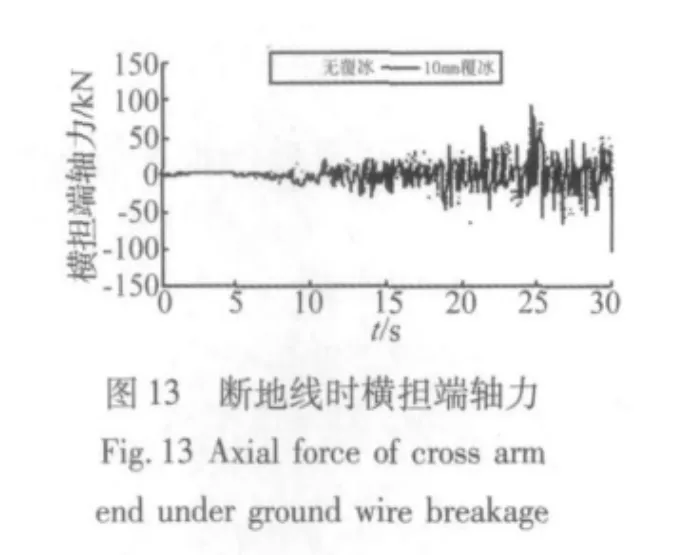
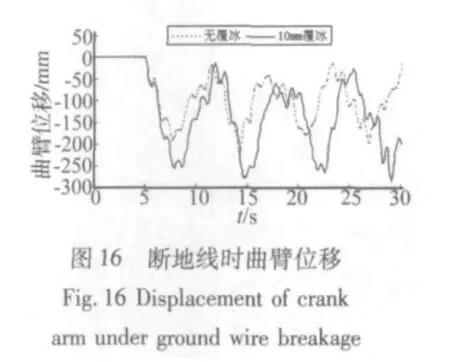
当无覆冰断地线时，塔腿轴向压力最大值为-546.377 kN;10 mm覆冰断地线时，塔腿轴向压力最大值为-713.71 kN，增加了30.63%，曲臂处和横担端轴力极值增加了9.0%和61.71%。由此可见，覆冰断地线时对铁塔轴力的冲击响应影响较大。

图14给出了无冰断导线和断地线时塔头轴力响应，从图中可以看出，断导线的轴力响应要明显大于断地线的轴力响应，对于覆冰断线时，结果相似。图15和图16提取了无冰和10 mm覆冰断地线工况下，2#铁塔塔头和曲臂处的位移时程曲线，由图可见，断线后塔头摆动位移最大，无冰断地线时位移的最大幅值为877.4 mm，10 mm覆冰断地线时位移最大幅值为1 157.8 mm，位移增大了31.96%，因此覆冰断地线对铁塔的位移冲击也显著增大。

无论在10 mm覆冰断导线和断地线的工况下，断线后的轴力、位移响应均大于无覆冰时的响应。线路覆冰后断线冲击更加剧烈。覆冰断线对于输电杆塔的轴力、位移均产生很大的冲击作用。

为了定量评价上述几种工况下铁塔各控制位置杆件的断线响应，引入了冲击系数η的概念，冲击系数可定义为:

其中η表示冲击系数，N1为断线工况下某杆件轴力最大值的绝对值，N0为导地线自重荷载或冰重荷载情况下某杆件轴力值。

由于2#塔临近断线点，所受冲击响应最大，因此提取在无覆冰断线及10 mm覆冰断线工况下各控制截面轴力响应最大值，按式(17)求得的无覆冰断线和覆冰断线的冲击系数η1和η2，结果见表2。

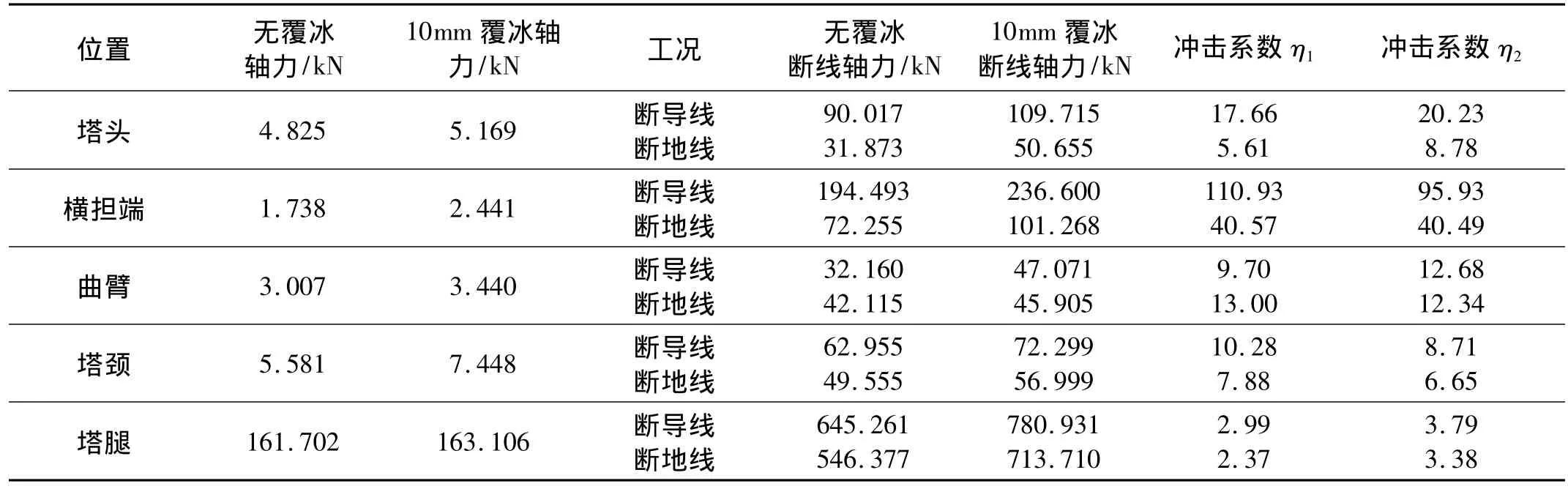
表2 2#塔控制截面轴力和冲击系数Tab.2 Axial force and impact coefficient of controlling section of tower 2#

4 结论

(1)本文以等效单根导线代替分裂覆冰导线，利用能量方法，建立了大跨越高压输电线路覆冰断线的冲击动力学模型，以某一大跨越高压输电线路为例，计算了无冰和10 mm覆冰断线时铁塔主要控制截面的内力和位移响应，为覆冰断线分析提供了一种有效的计算方法。

(2)从计算结果来看，覆冰时导地线断裂产生的冲击效应要明显大于无冰断线情况，导线断线产生的冲击效应要明显大于地线断线的冲击效应，对于输电杆塔来说，塔腿、塔颈部、横担端、上下曲臂交点是轴力冲击影响最严重的位置，而塔顶和横担端导线断线点是冲击位移影响最严重之处，故对于重冰区应适当提高这些部位的强度、刚度和稳定性设计等级，以抵抗覆冰断线造成的灾害。

(3)本文建立的冲击动力学模型为研究高压输电线路在各种环境荷载下作用下导地线断线冲击动力响应计算和工程应用提供了参考。同时也为大跨越高压输电线路覆冰断线试验分析和数值模拟提供理论依据。

［1］苑吉可，蒋兴良，易 辉，等.输电线路导线覆冰的国内外研究现状［J］.高电压技术，2004，30(1):6-9.

［2］Oswald B，Schroeder D，Catchpole P.Investigative summery of the july 1993 nebraska public district grand island moore 345kV transmission line failure［C］//.Transmission and Distribution Conference，Proceedings of the 1994，IEEE Power Engineering Society，1994，574-580.

［3］胡 毅.电网大面积冰灾分析及对策探讨［J］.高电压技术，2008，34(2):215-219.

［4］中华人民共和国电力行业标准，《架空送电线路杆塔结构设计技术规定》(DL/T5154-2002)［S］.北京:中国电力出版社，2002.

［5］国家电力公司华东电力设计院.《110 kV～500 kV架空送电线路设计技术规程》(DL/T5092-1999)［S］.北京:中国电力出版社，1999.

［6］Peyrot A H，Kluge Robert O，Lee Jun W.Longitudinal loads from broken conductors and broken insulators and their effect on transmission lines［J］.IEEE Transactions on Power Apparatus and Systems，1980，99(1):222-234.

［7］ Mozer J D，Wood William A，Hribar John A.Broken wire tests on a model transmission line system ［J］.IEEE Transactions on Power Apparatus and Systems，1981，100(3):938-947.

［8］ Fleming John F，Mozer A R S，John D.A program for longitudinal load analysis of electric transmission lines［J］.Computers and Structures，1978，9(3):237-253.

［9］ Siddiqui F M A，Fleming John F.Broken wire analysis of transmission line systems［J］.Computers and Structures，1984，18(6):1077-1085.

［10］ Thomas M B，Peyrot A H.Dynamic response of ruptured conductors in transmission lines［J］.IEEE Transactions on Power Apparatus and Systems，1982;PAS-101(9):3022-3027.

［11］ McClure G，Tinawi R.Mathematical modeling of the transient response of electric transmission lines due to conductor breakage［J］.Computers and Structures，1987;26(1/2):41-56.

［12］ McClure G，Lapointe M.Modeling the structural dynamic response of overhead transmission lines［J］.Computers and Structures，2003，81(8-11):825-834.

［13］夏正春，李 黎，梁正平，等.输电塔在线路断线作用下的动力响应［J］.振动与冲击，2007，26(11):45-49.

［14］李 黎，夏正春，江宣城，等.输电线断线振荡研究［J］.工程力学，2008，25(6):165-169.

［15］沈国辉，何运祥，孙炳楠，等.绝缘子断裂对大跨越输电线路的动力效应［J］.浙江大学学报，2008，42(11):1990-1995.

［16］沈国辉，莫增禄，孙炳楠，等.突然断线对输电塔线体系的冲击作用研究［J］.振动与冲击，2009，28(12):3-8.

［17］ Veletsos A S，Darbre G R.Dynamic stiffness of parabolic cables［J］.Journal of Earthquake Engineering and Structure Dynamics，1983，11(3)，367-401.

［18］ Gortemaker P C M.Galloping conductors and evaluation of the effectiveness of in-span dampers［C］.Kema Science and Technology Report，1984，2(4)，27-39.