振荡压气机叶栅叶片表面非定常响应以及气弹稳定性分析

郑 赟，杨 慧，田 晓

(北京航空航天大学 能源与动力工程学院发动机数值仿真中心，北京 100191)

叶片颤振与由叶片振动引起的非定常流动密切相关。一般认为叶片颤振是一种流体诱发的自激振动，通常称为叶片气弹稳定性问题，它是伴随叶轮机发展的经典难题。在叶片振动过程中，从流体吸收的能量大于包围叶片的流体和叶片根部对叶片做的阻尼功时，颤振发作，最终可能导致结构性破坏。叶片颤振问题常常会影响叶轮机的风扇、压气机前几级和具有相对长叶片的低压涡轮后几级叶片。与强迫振动不同，颤振与发动机转速不相关并覆盖相对广的发动机工作范围［1］。

传统上，借鉴以往机翼失速颤振的经验，通过由试验并结合经验公式或半经验公式得到的经验“设计准则”预测和避免颤振发生。根据经验将每一个气动条件下的叶片特征截面的折合频率与相对进口马赫数(或攻角)相关联以确定颤振边界［2］。但这种方法不足以用来理解叶轮机内部真实流动的非定常特性，例如激波附面层干扰的粘性效应对非定常流动特性的影响;而过保守的设计往往以牺牲发动机性能为代价;并且其结果无法外推于新机型。

近年来，高推重比［3］的设计趋势，以及新颖轻质叶片刚度降低，这些因素都增加了叶片颤振发生的可能性。为提高级增压能力而使用跨音叶片，会引发超音非失速颤振，可以在任何压比下发作，并穿过压气机工作线，威胁着压气机的高速运转［4］，设计者必须在工作点或其附近对此类颤振进行检验。振荡激波周围强烈的非定常负荷是这类颤振最显著的特点。对于风扇/压气机叶片的跨音工作状态，研究激波对振动叶片非定常响应的影响有着重要的工程意义。因此，发展新机型的需求迫使叶片颤振分析与预测技术必须有所突破。发展以理解叶片颤振内在物理机制为基础的数值预测方法尤为必要，可有效地、低风险地协助工程技术人员减少地面试验次数，进行工程仿真，以及更好地理解气体的流动过程，是有效的颤振主动控制技术的基础。

基于目前对叶片颤振物理机制的认识，数值模拟的气动弹性分析模型大致分为三种:能量法［5］、特征值法［6］与流固耦合方法［7-9］。无论哪种颤振预测方法都要涉及叶片振动引起的非定常气动响应分析。早期只有分析法和半分析法，而这些方法只能应用于无载荷的平板这样的简单结构［10］。

近二十年来，随着信息技术、硬件和计算方法的发展，利用非定常CFD技术对振动叶栅非定常绕流进行数值模拟，提供流场详细信息，分析振动叶片与周围流场间的相互作用，国内外取得了一定进展，涌现了大量近似程度不同的非定常气动模型［11-14］。其中非线性时间推进法因其可以模拟强非线性(如分离和激波)，而得到广泛应用［13-15］。但是以理解颤振发作机理，寻找颤振影响主导因素为目的的实验研究和数值模拟研究都开展的不多。对压气机振动叶栅进行多参数，多振动形式，多流态的全面分析是十分必要的。折合频率(k)是描述非定常流动问题的重要参数。对于叶片颤振，定义为叶片振动频率与流速的比值，典型的一阶弯曲振动的折合频率为0.3，一阶扭转振动大约为1，流动的非定常性的影响很显著。而叶片间相角(IBPA)又是描述振动叶片间气动耦合的重要参数。为此本文使用时间推进法，选取气弹标准算例集［16］中10号实验—高亚音/跨音流的振荡压气机叶栅为分析对象，研究叶片做弯曲振动，不同的影响参数，如流动状态、折合频率和IBPA，对振荡叶栅叶片表面非定常响应以及气弹稳定性的作用。

1 流动模型及数值算法

不包括彻体力和外部热源，一般曲线坐标系下的三维可压缩非定常N-S方程为:

式中t为时间为守恒变矢量，代表单位体积的密度、动量和总能量;为无粘矢通量，，为粘性矢通量，压力p由理想气体状态方程获得。对于湍流，选择了计算效率和精度都较好的一方程 S-A模型。

非定常可压缩N-S方程的求解基于多块结构化网格的有限体积方法，它的优点是计算速度较快，精度较高。对流通量的计算采用了ROE的迎风格式，粘性通量使用二阶中心差分法。多重网格算法用于加速定常流动计算和非定常计算中子叠代的收敛。

为了提高非定常流的时间精度，又具有较高的计算效率，使用了基于Jameson等人提出的双时间步方法，在每个物理时间步进行4～15次虚拟时间步的牛顿子迭代以提高格式的时间精度。时间推进格式使用三点后差的二阶格式。

在求解振动结构的非定常流动时，由于固体边界随时间变化，需要流体网格进行相应的变形以保证计算的正常进行，通常是对上一时间步的网格进行微调以适应物面的变形，本文采用了基于弹簧法的多块协调变形技术以动态调整网格内点，以保证叶片表面变形不会引起网格失效。

2 标准算例10介绍及计算网格

气弹标准结构10(STCF10)的叶片为改进的NACA0006翼型(如图1所示)，圆弧形的叶型中弧线，最大高度为弦长的5%。叶栅几何参数见表1。

表1 STCF10叶栅几何参数Tab.1 Geometrical parameters of cascade STCF10

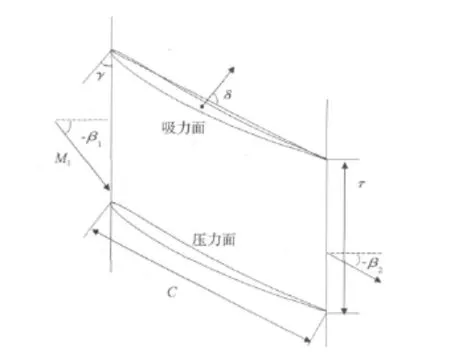
图1 标准算例10叶栅几何结构Fig.1 Geometry of cascade STCF10

图2为一个通道的计算网格，节点数为237(流向)×79(周向)。非定常流动模拟，选择高亚音和跨音两种流动状态，对应每个流态，选取4个折合频率，每个折合频率下，又选取两个叶片间相位角，共16种工况(见表2)。在每一个非定常流动工况模拟之前，先进行定常流动模拟，其结果作为非定常模拟的初始流场，以加快其收敛速度。定常流动数值模拟中，按照实验数据，给定进口总温、总压和来流进气角，出口给定静压。

图2 标准算例10的单通道计算网格Fig.2 Multi-block grid for a single passage of STCF10

非定常流动模拟根据叶片间相位角(IBPA)的要求，增加通道个数，在周向边界上施加周期性边界条件，进出口的边界条件与定常计算相同。按照实验给定的弯曲振动方向和振幅，利用网格变形技术控制流场网格随叶片运动的变化。非定常计算达到周期稳定一般需要三到四个振动周期，然后输出一个周期内叶片表面的压力随时间的变化历程，根据式(2)进行傅里叶变换，得到非定常压力第一阶谐频的幅值F1，以及与振动位移的相位差φ1。

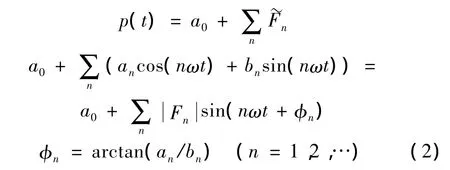
根据叶轮机械颤振特点，气弹稳定性分析广泛使用能量法［17］。其忽略非定常气动力对振动模态的影响，通过获得叶片表面气动力对叶片所做的功判断结构的气弹稳定性，气动功为正，则振动发散。本文用其考察各关键参数对振荡叶栅气弹稳定性的影响。

假设振动位移为s=Asin(ωt)，在一个振动周期内非定常力在位移s上做的功为:

由式(3)可以看出，气动功的正负取决于sinφ1的正负，是气弹稳定性的标志。当吸力面相位在0°至180°之间，表示非稳定，压力面表示稳定;当吸力面相位在(-180°)至 0°之间，表示稳定，压力面表示非稳定。

表2 非定常实验参数Tab.2 Unsteady experimental parameters

3 STCF10亚音流动分析

3.1 亚音定常流动分析

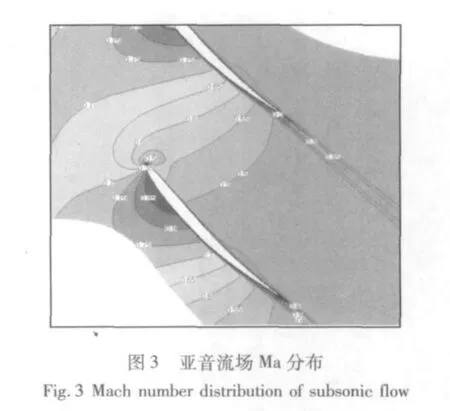
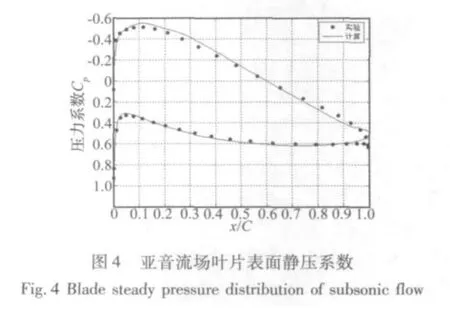
数值模拟的亚音流场马赫数分布如图3所示，在压气机叶栅中，气流在吸力面的前10%弦长，压力面前5%弦长加速降压，此后随着通道扩张，气流开始不断减速增压。叶片表面静压分布与实验数据的对比见图4，总体上，亚音工况叶片表面压力系数的模拟结果与实验数据吻合很好。

3.2 亚音非定常流动分析

IBPA为0°时，在振动周期的任意时刻叶栅中每个叶片的运动方向一致，气流通道的大小不随时间改变。

非定常压力幅值见图5。k为0.25，压力幅值的峰值，在压力面和吸力面的叶片前缘处。随着折合频率k的升高，整个叶片的非定常压力幅值都增加，表明非定常扰动效应随k而增加。当非定常扰动效应达到最大(k=1)时，吸力面的峰值由叶片前缘向叶中(20%～35%弦长)移动，压力幅值沿吸力面和压力面的弦向分布规律充分体现了叶片静载的影响，表明改变叶片静载分布将影响叶片的气弹稳定性。

当k=0.25时，(见图6)压力面尾缘处非定常压力相位角领先，压力面起稳定作用，吸力面前35%弦长起稳定作用。随着折合频率k的提高，两个表面的相位不断下移，增加到1时，压力面前缘10%弦长起失稳作用，吸力面前70%弦长起稳定作用。并且，缩减了吸力面弦长10%到尾缘处的弦向相位差异。由于压力面前缘相位角随折合频率的增加减小得比较快，当k=1时，压力面与吸力面前缘之间的相差由近180°降为 120°。

IBPA=90°，k=0.25 时(图7)，压力面压力幅值的形状与IBPA=0°(图5)相比，没有变化，吸力面弦向变化趋势比IBPA=0°平滑。压力幅值水平比IBPA=0°有所提高，表明IBPA从0°变为90°，气流通道大小在振动周期的每一时刻都发生变化的非定常性减弱了静载对非定常响应的影响。随k升高静载对非定常响应加强的特征，在IBPA=90°仍有体现。

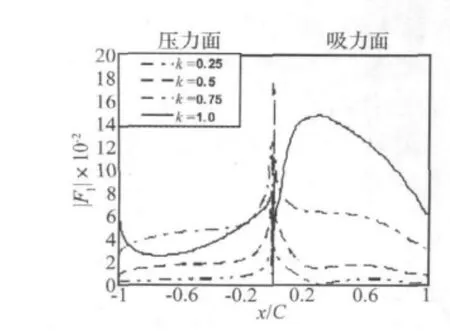
图5 非定常压力幅值(亚音工况:IBPA=0°)Fig.5 Amplitude of unsteady pressure(subsonic flow:IBPA=0°)

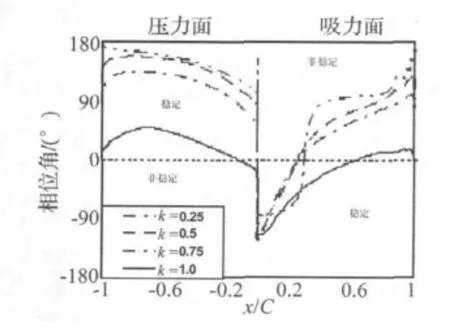
图6 非定常压力相位(亚音工况:IBPA=0°)Fig.6 Phase of unsteady pressure(subsonic flow:IBPA=0°)

图7 非定常压力幅值(亚音工况:IBPA=90°)Fig.7 Amplitude of unsteady pressure(subsonic flow:IBPA=90°)

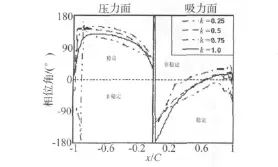
图8 非定常压力相位(亚音工况:IBPA=90°)Fig.8 Phase of unsteady pressure(subsonic flow:IBPA=90°)

k=0.25时，与IBPA=0°相比，压力面相位角弦向差异变大(见图8)，表明叶片间气动耦合增加了非定常的弦向波动。随k增加，压力面中段各点相位弦向差异变化不大，尾缘和前缘弦向差异增加，但压力面相位整体没有平移，叶片间相位角与k增加对非定常效应的作用是相反的。

在低折合频率(k=0.25)，随IBPA通道变化，吸力面弦向各点之间的相位差异减小，同样表明IBPA引起的气流通道变化减弱了静载的非定常效应。随着k增加，吸力面前半弦长各点之间的相位差异增加，90%弦长以后尾缘的相位角曲线不平滑现象(对应尾缘分离区)随着k的增加有所改善。吸力面前缘相位只在k=1时发生平移。表明高k时，IBPA通道变化加强了静载的非定常效应。

4 STCF10跨音流动分析

4.1 跨音定常流动分析

跨音流动数值模拟的定常流场分布如图9所示。吸力面前缘气流不断加速降压，在20%-25%弦长处产生一道激波。计算所得的叶片表面的静压分布与实验数据的对比见图10。数值模拟的激波位置和激波强度与实验基本相符。

图9 跨音流场Ma分布Fig.9 Mach number distribution of transonic flow

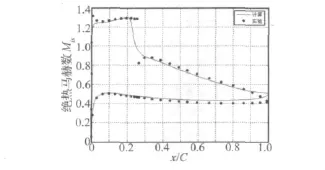
图10 跨音流场叶片表面绝热Ma分布Fig.10 Isentropic Mach number distribution at the wall(transonic flow)

4.2 跨音非定常流动分析

IBPA=0°时，k=0.25，在吸力面 12% 弦长处，压力幅值和相位角(见图11和图12)都有突跃，对应于非定常压力时均图(图13)的激波突跃处。在时均线和定常线交叉点之后的10%弦长，弦向相位没有差异。

对比图5，跨音流的非定常压力幅值在叶片两个表面上都比亚音流高。这是由于跨音条件下，叶片静载高于亚音流。

跨音流压力面的弦向相位差异比亚音流动大(对比图12和图6)。由于激波的非定常响应，在两个表面上相位都发生了平移，并与亚音流对稳定性的贡献相反，比如压力面由亚音的稳定相区移向不稳定，吸力面前半弦长由亚音的稳定相区移向不稳定，后半弦长由亚音的不稳定相区移向稳定。

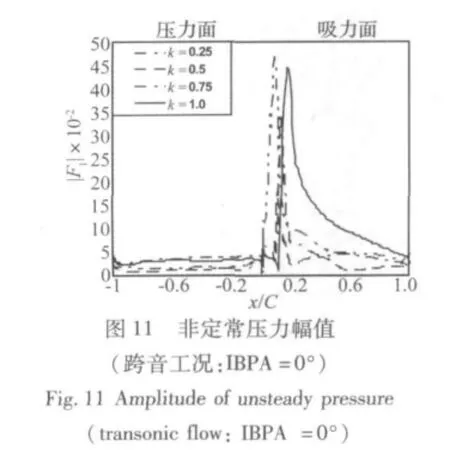
对于k=0.25，IBPA由0°变为90°对压力面幅值的影响不大(对比图11和图14);对吸力面，加大了激波后幅值的弦向差异。吸力面激波峰值的弦向位置与压力时均值相对应，而亚音流动对应的是定常流(图16)。对比图13和图16发现，不同叶片间相位角下由于激波的非定常响应不同，造成非定常压力时均值也不一样。随k的增加，压力面前缘幅值增加，尾缘变化不大，导致弦向差异加大;吸力面，k大于0.5时，激波突跃数值增大，激波后的波动被抹平，弦向差异随k增加加大，此与IBPA=0°(图11)的规律一致。对于吸力面，IBPA不但提高了激波峰值，而且增加了激波的弦向影响范围。

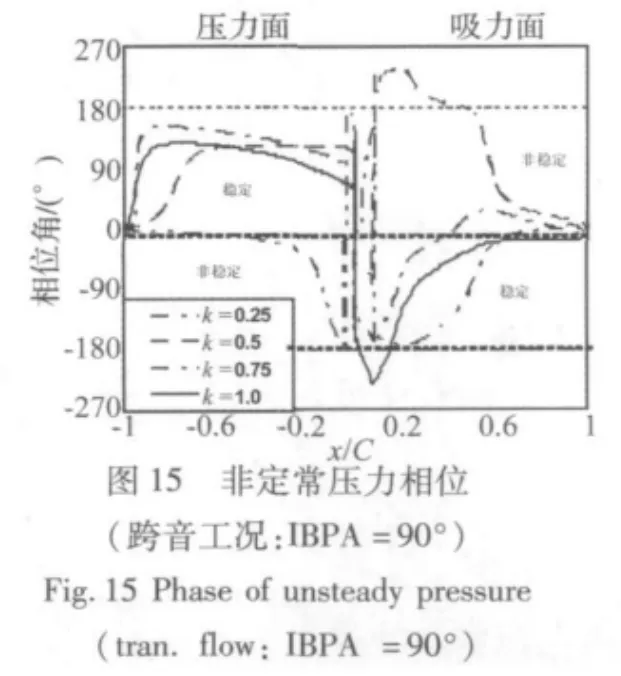
IBPA的改变对于k=0.25的非定常压力相位角的影响表现为，加大了压力面前20%弦长相位和吸力面后50%弦长的弦向差异(图15)，减小了压力面20%弦长以后相位的弦向差异。随折合频率的增加，叶片两个表面的相位角走势与IBPA=0°时(图12)相似，与亚音流动下，叶片间相位角的作用不同。亚音流下叶片气动耦合加强时(IBPA=90°)非定常压力相差不随折合频率增加而变化的规律，在跨音流下由于k对激波非定常响应的作用抵消了IBPA的通道效应，因此IBPA的影响主要通过改变非定常压力幅值的大小来体现。

5 STCF10气弹稳定性分析

图17为叶片做弯曲振动，16种非定常流动工况下，压气机叶栅的气动功。以能量法为基础，由一个周期内叶片表面气动力对振动叶片所做的功得到。由图可知，跨音工况，IBPA=0°，k=0.25 时气动功为正，最不稳定;亚音工况，IBPA=90°，k=1时气动功为负的最大值，最稳定。除去亚音工况，IBPA=0°，k=1的情况，同一IBPA，亚音工况比跨音工况稳定。两种流态，同一IBPA下，对于k的变化趋势是一致的。对于两种流动工况，叶片间气动耦合较弱时(IBPA=0°)，折合频率增加引起的气动功负向递增，即结构稳定性增加，在k=1时，发生了改变。通过以上叶片表面非定常响应分析可知，折合频率对气弹稳定性的影响主要通过平移非定常压力相差来实现。当叶片间气动耦合较强时(IBPA=90°)，高k时(k=1)，IBPA引起的通道效应抵消了折合频率的非定常效应，加强了静载的非定常效应，导致气动功依然负向递增。

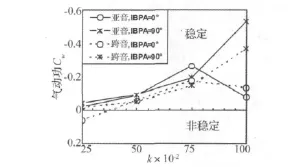
图17 STCF10气动功Fig.17 STCF10 aerodynamic work

6 结论

本文通过数值模拟压气机叶栅在弯曲振动下，多种影响参数对叶片表面非定常响应及叶栅气弹稳定性的作用。得到如下结论:

(1)在亚音流动下，非定常压力幅值沿吸力面和压力面的弦向分布规律体现了叶片静载的影响。

(2)折合频率增加的非定常效应体现在增加叶片表面的非定常幅值，整体平移相位角。主要由两个表面相位角所处的区域是否稳定决定结构的气弹稳定性。

(3)在跨音流下，在激波附近，非定常时均流场与定常流场不同，随折合频率以及叶片间相位角不同而变化。激波在叶片表面有很强的非定常响应，其响应点与时均流场相关，而不是定常流场。

(4)跨音振荡叶栅中，激波对结构气弹稳定性的影响主要取决于非定常压力相差，在此压气机结构中激波起非稳定作用。激波对结构的非定常效应，抑制了折合频率所强化的通道非定常效应。

(5)在此叶栅中，同一折合频率下，叶片间相位角的通道非定常效应与激波的失稳作用，静载的非定常效应，k增加的非定常效应相互抵消。但在高折合频率下(k=1)，叶片间相位角引起的强气动耦合却加强了静载的非定常效应，导致结构气弹稳定性增加。

(6)由分析可知，关键参数对结构气弹稳定性的影响不是独立作用，而是多个参数相互耦合作用的结果。这也是颤振机理研究的难点与关键点。

［1］Srinivasan A V.Flutter and resonant vibration characteristics of engine blades［R］.ASME Paper，1997，97-GT-533.

［2］Mikolajczak A A.Technology status for blade flutter in axial turbomachinery［J］.Journal of Fluids Engineering，1976，98:337-339.

［3］陈 光.航空发动机结构设计分析［M］.北京:北京航空航天大学出版社，2006.

［4］Kielb R E.CFD for turbomachinery unsteady flows-an aeroelastic design perspective［R］.AIAA paper，2001.

［5］Clark W S，Hall K C.A time-linearized navier-stokes analysis of stall flutter［J］.Journal of Turbomachinery，2000，122:467-476.

［6］Bleeg J M，Yang M T，Eley J A.Aeroelastic analysis of rotors with flexible disks and alternate blade mistuning［J］.Journal of Turbomachinery，2009，131(1):11-19.

［7］郑 赟.基于非结构网格的气动弹性数值方法研究［J］.航空动力学报，2009，24(9):2069-2077.

［8］Johnston D A，Cross C J，Wolf J M.A architecture for fluid/structure interaction analysis of turbomachinery blading［R］.AIAA paper，2005，2005-4013.

［9］金 琰.叶轮机械中若干气流激振问题的流固耦合数值研究［D］.北京:清华大学，2002.

［10］ Peter D S，Chae M R，George S C，et al.CFD investigation of aeromechanics［R］. ASME paper，2001-GT-0267，2001.

［11］ He L，Chen T，Wells R G，et al.Analysis of rotor-rotor and stator-stator interference in muti-stage turbomachines［J］.Journal of Turbomachinery，2002，124:564-571.

［12］ Hall K C，Clark W S，Lorence C B.A linearized Euler analysis of unsteady transonic flows in turbomachinery［J］.Journal of Turbomachinery，1994，116(3):477-488.

［13］ Sanders A J，Hassan K K，Rabe D C.Experimental and numerical study of stall flutter in a transonic low-aspect ratio fan blisk［R］.ASME paper，2003，GT2003-38353.

［14］胡运聪，周新海.二维振荡叶栅非定常粘性流动数值模拟［J］.应用力学学报，2003，20(3):79-81.

［15］ Gru ber B，Carstens V.The impact of viscous effects on the aerodynamic damping ofvibrating transonic compressor blades-a numerical study［J］.Journal of Turbomachinery，2001，123:409-417.

［16］ Bolcs A，Fransson T H. Aeroelasticity in turbomachines comparison of theoretical and experimental cascade results［C］.Communication du Laboratoire de Thermique Appliquée et De Turbomachines，Nr.13，Lausanne:EPFL，1986.

［17］张 潇.基于能量法的叶片颤振边界预测方法［D］.北京:北京航空航天大学，2008.