基于小波变换和反向传播网络的模态参数辨识

代 煜，张建勋

(南开大学 机器人与信息自动化研究所，天津 300071)

小波变换是一种能对观测信号进行时频联合分析的方法，系统的自由衰减响应信号在连续小波变换域上的系数分布呈现出脊的特征，由此发展出多种根据脊上小波变换系数的相位、幅值信息使系统自动解耦，并提取线性系统的模态参数［1-3］或弱非线性阻尼及刚度［4］的方法。

在对系统的自由衰减响应信号进行小波变换时，小波变换系数必然会受到边界效应的影响。边界效应产生的根本原因是小波变换中的卷积运算，实际采集的信号都是在时域离散而且有限长的，对这样的序列作卷积相当于加矩形窗，因此在小波变换系数的两个边界处会发生畸变，这必然影响到模态参数的识别。对于模态参数识别中遇到的边界效应问题，目前主要有以下几种解决方案:Boltezar和Slavic［5］提出用反射窗法、等窗面积法和自适应小波函数法来改变小波函数以消除边界效应;伊廷华等［6］提出运用自回归滑动平均模型进行信号预测以消除边界效应的影响;徐增丙等［7］提出运用最小二乘支持向量机对小波骨架进行预测延拓的方法;Kijewski和Kareem［8］提出采用镜像延拓技术以消除边界效应对小波变换系数的影响;Yan等［9］定量计算了不受边界效应影响的小波变换系数的范围，指出只有这部分系数才能用于估计模态参数，其余受到边界效应影响的部分应当剔除。这几种方法可以分为两类:一类是通过调节小波函数中的参数实现对边界效应的抑制，一类是对信号进行延拓以获得较多不受边界效应影响的小波变换系数。受到种种条件的限制，小波函数的改变程度有限，因此研究信号的延拓方法是克服边界效应的最重要途径。在众多的延拓方法中，类似镜像法、补零法的一些方法不具有对待分析信号的自适应性，这将对模态参数的估计精度带来一定程度的影响。

考虑到人工神经网络具有通过自学习逼近任意映射的能力，突破了需要建立参数模型的传统方法，本文将利用反向传播网络对采样时长较短的自由衰减响应信号进行双向延拓，然后对信号进行连续小波变换，从而提取各阶模态的阻尼比和无阻尼自振频率。

1 基于连续小波变换的模态参数识别方法的理论基础

小波变换是一种能对信号进行多尺度(分辨率)分析的线性变换。设ψ(t)是L2(R)(L2(R)表示平方可积的函数空间)内的实值或复值函数，当且仅当ψ(t)的傅里叶变换ψ^(ω)满足以下不等式时函数ψ(t)可以成为母小波:

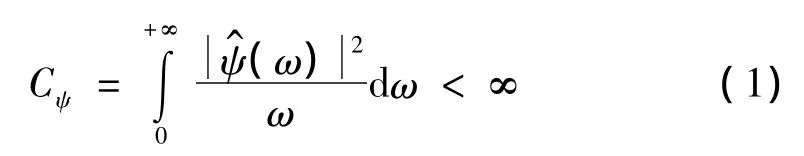
函数x(t)∈L2(R)在尺度因子为a，时移因子为b时的连续小波变换Wx(a，b)表示为:

式中，a，b和t均是连续变量，且a＞0，ψ*(·)表示复共轭，〈·〉表示卷积。本文采用最常用的Morlet复小波作为母小波，定义如下式所示:

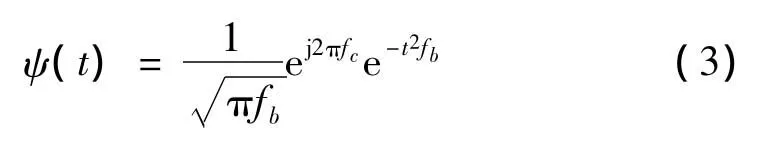
式中fc为小波中心频率，fb为带宽参数，j是虚数单位。二者都可因分析对象的不同而改变，这就提供了极大的灵活性。

线性多自由度系统的自由衰减响应为［9］:

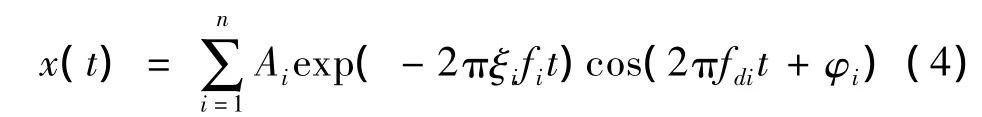
式中Ai表示第i阶模态的振幅，φi表示初相角，fi是第i阶模态的无阻尼自然频率是有阻尼自然频率，ξi表示阻尼比，n表示模态的阶数。根据渐进信号的相关理论［10］，x(t)的Morlet小波变换系数的近似表达式为:

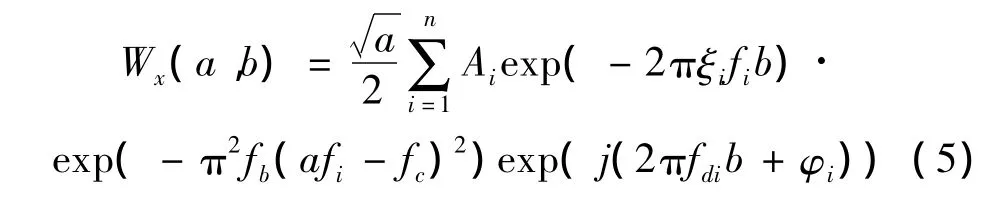
由式(5)可见，对于每一个时移因子b，在尺度ai=取得局部极大值，因此可以提取到小波脊，并且认为在这个尺度下仅有第i阶模态的响应决定着小波变换系数，其余(n-1)个模态的影响可以忽略不计，此时多模态被解耦。因此，尺度为ai时的小波变换系数可以表示为［9］:

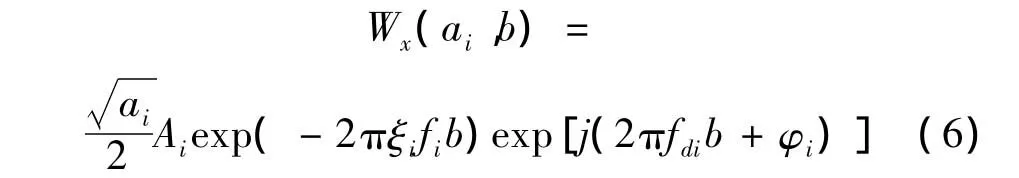
小波变换系数的模和辐角可表示为［9］:

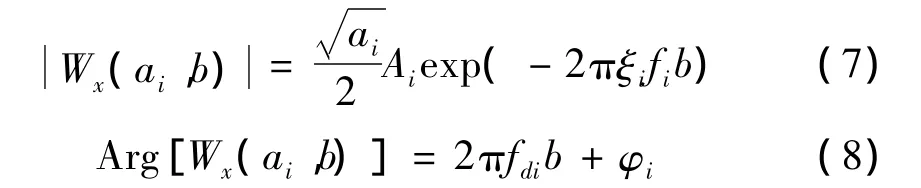
对式(7)和式(8)应用对数和微分运算，第i阶模态的无阻尼自然频率fi和阻尼比ξi由下式估计［9］:

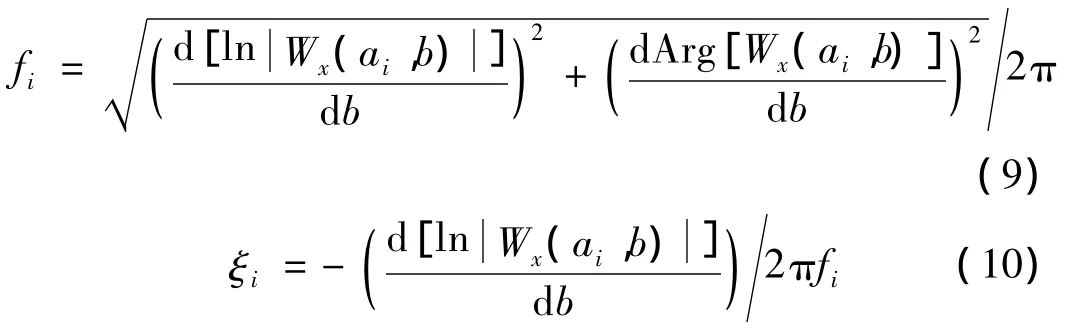
式中ln［·］表示取自然对数，Arg［·］表示求辐角。

为了分离信号中两个较接近的频率成份fi和fi+1，可以通过改变fb和fc提高频率分辨率，但同时时间分辨率会下降，时间分辨率下降带来的后果是边界效应更加严重。Yan等［9］研究了时频分辨率对模态解耦和边界效应的影响，计算了小波参数的选择范围，如式(11)所示:

式中，α、β和γ均是用于调节范围的常数:α=2、β=4和γ=0.4;T表示自由衰减响应信号的采样时长。此外，为满足小波函数的容许性条件，还应当使。Yan 等［9］还给出了边界效应的影响范围:

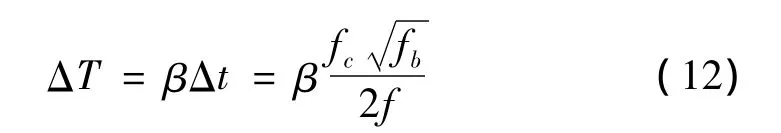
式中，f表示小波分析窗的中心频率。值得注意的是，当待分析信号的采样时长较短或者模态较密集时，式(11)将会无解，因此必须考虑增加信号的采样时长。

2 利用反向传播网络对信号的双向延拓

利用反向传播神经网络对自由衰减响应信号的延拓建立在一定数量的信号样本之上。神经网络的实质就是依据已有的样本数据，通过训练获得并存储样本所隐含的特征关系，因此它具有很强的学习适应能力。

本文提出的用于信号延拓的三层反向传播网络模型如图1所示，由输入层，隐藏层和输出层组成，同层神经元间无联系，前后层间全连接。图1中输入层样本的个数p表示前p个信号的离散采样点对下一个采样点有直接影响，而最新观测值将比早期观测值包含更多信息。网络中隐藏层的传递函数都采用S型正切函数:

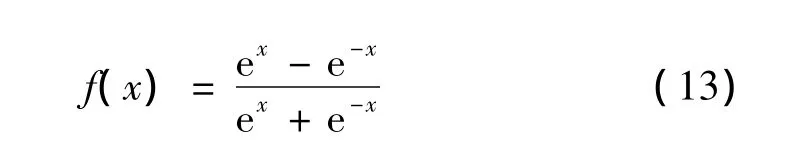
输出层用线性传递函数。对于在0到T时刻等时间采样的信号序列{x(1)，x(2)，…，x(q)}，利用反向传播网络对信号进行双向延拓的步骤如下:

(1)离散时间序列的归一化处理。为了避免神经网络的不稳定性及收敛速度慢等问题，必须先对原始数据进行归一化处理。本文通过式(14)将原序列变换到［0，1］区间:

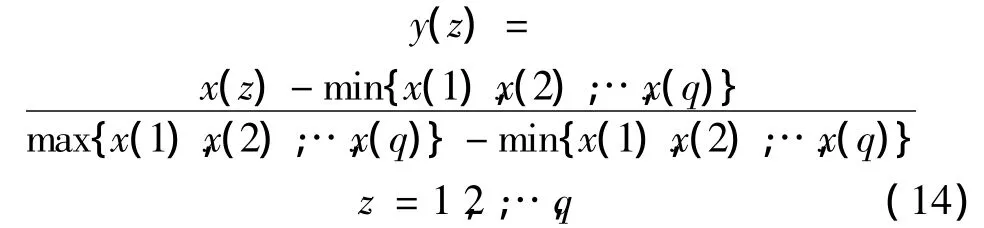
式中，max{·}和min{·}分别表示求序列的最大值和最小值。

表1 反向传播网络的训练样本(1)Tab.1 Training samples of back propagation network(1)

表2 反向传播网络的训练样本(2)Tab.2 Training samples of back propagation network(2)

(2)对反向传播网络的训练。从上一步骤得到的序列{y(1)，y(2)，…，y(q)}中获取训练样本，如表1和表2所示，表1中的p个训练样本用于预测在T时刻之后的信号序列，而表2中的p个训练样本用于预测在0时刻之前的信号序列。训练样本由输入层经隐藏层传递到输出层，输出层将训练结果与期望值进行比较，按照减少误差的方向，从输出层反向经隐藏层修正各连接权值，最后回到输入层，这个过程反复进行，直到反向传播网络的输出误差小于设定值时才认为训练完成。

(3)对信号序列的双向延拓。为预测T时刻之后的h点信号序列，对上一步骤中训练完的网络依次输入{y(q-p+1)，y(q-p+2)，…，y(q)}，{y(q-p+2)，y(q-p+3)，…，y(q+1)}，…，{y(q-p+h)，y(q-p+h+1)，…，y(q+h-1)};为了预测0时刻之前的h点信号序列，对上一步骤中获得的另一个反向传播网络依次输入{y(p)，y(p-1)，…，y(1)}，{y(p-1)，y(p-2)，…，y(0)}，…，{y(p-h+1)，y(p-h)，…，y(2-h)}。双向延拓的好处在于，它能够使得原始信号序列的小波变换系数不受边界效应的影响，而受到边界效应影响的小波变换系数均来自于对延拓信号序列的连续小波变换，这就能够使得原始信号的小波变换系数对最终模态参数识别结果的贡献最大。

(4)通过式(15)将神经网络输出序列的幅度还原:

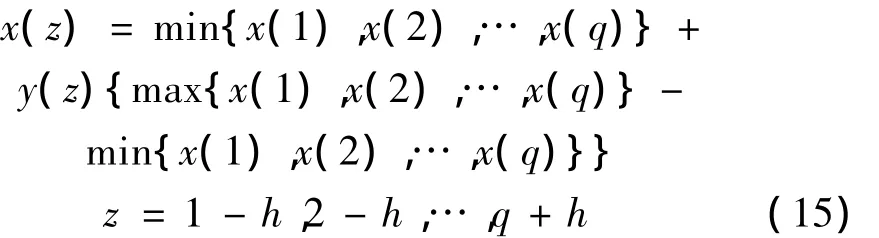
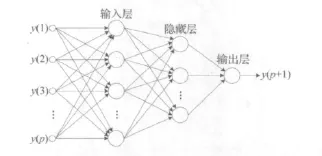
图1 用于信号双向延拓的反向传播网络Fig.1 Back propagation network developed for signal extension in both directions

3 数值仿真

两自由度有阻尼系统的自由衰减响应如式(4)所示，令式中i=2;f1=10 Hz;ξ1=0.005;φ1=π/6;f2=12 Hz;ξ2=0.01;φ2= π/4;Ai=1(i=1，2);采样频率fs=200 Hz以及采样时长T=1.5 s。将这些数据代入式(11)，无解。对于图1所示的反向传播网络，输入层的神经元个数设为40，隐藏层的神经元个数为5，利用表1和表2中的样本对神经网络进行训练，取p=200。初始学习速率参数设置为0.05，动量系数设为 0.9，目标误差设为 1 ×10-4［11］。图 2 给出了利用反向传播网络对信号进行双向延拓的结果(延拓序列的长度h=100)，图中两条竖线间的区域是原始信号，实线是延拓的信号，虚线表示该自由衰减响应信号的理论幅值。从图2中可见只是在信号幅度的突变处延拓的信号与其理论值有少量差异，其余时刻二条曲线基本吻合。将信号的采样时长改为2.5 s，代入式(11)解得3.5≤≤5。根据式(12)计算得到边界效应的影响范围，将这部分受到边界效应影响的小波变换系数剔除，而后利用式(9)和式(10)辨识各阶模态的阻尼比和无阻尼自振频率。

考虑到实际采集的自由衰减响应信号常常被噪声污染，表3给出了不同噪声水平下模态参数识别的相对误差，所加的噪声为零均值的高斯噪声。信号的噪声水平由信噪比(SNR)来衡量，SNR定义为信号标准差与噪声标准差的比值［12］。设r表示某个量的精确值，r0表示它的测量值或者估计值，相对误差定义为:

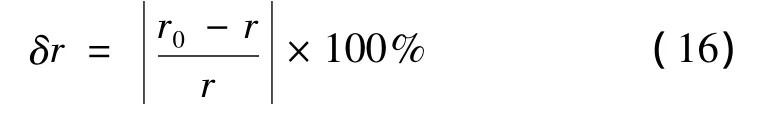
从表3可见，基于反向传播网络的双向延拓方法削弱了边界效应对模态参数识别的影响，这种方法对于信号采样时长较短或者模态较密集的场合有效。值得注意的是，由于在信号幅度的突变处延拓信号的质量较差，这给阻尼比的估计带来一定影响。从提取模态参数消耗的时间来看，SNR越低，训练神经网络所需要的时间越长。

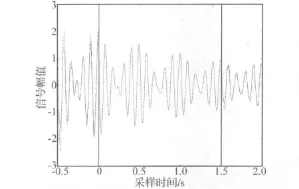
图2 利用反向传播网络对自由衰减响应信号的延拓Fig.2 Extension of free decay response signal using back propagation network

如果仅采用基于连续小波变换的模态参数识别方法，由于不能计算得到合适的，也就是边界效应将影响到所有的小波变换系数，这将导致模态参数识别结果的完全错误。如果采用直接设计神经网络辨识模态参数的方法，就必须要求一定数量的训练样本，如果训练样本的SNR和待辨识信号的SNR差距较大就不能得到较好的辨识结果，而小波变换能够在一定程度上克服噪声的影响，这就避免了单纯使用基于神经网络的辨识方法带来的不确定性。

4 实际问题的仿真分析

本文提出的模态参数识别方法在对用于微创外科手术机器人的力传感器的动态性能测试实验中得到了应用。具备力感知功能的四自由度微创外科手术机器手如图3所示，机器手通过右端的快换接口安装在微创外科手术机器人的机械臂末端，机械手中部是外径10 mm，长约500 mm的空心金属圆杆，手术开始时机器手经开在患者腹腔上的通道插入体内，由机器手左端钳形工具夹持手术针或其他器械完成整个手术。为了测量手术过程中钳形工具与患者内脏组织的接触力，将应变片阵列布置在圆杆表面上靠近钳形工具的位置，并对圆杆进行了必要的切削加工以满足应力集中和输入输出引线的需要。

表3 不同信噪比下模态参数识别的相对误差(fb=4，fc=2)Tab.3 Relative errors of identified modal parameters with different SNR(fb=4，fc=2)

力传感器的动态性能测试采用如下方法:将粘贴了应变片阵列的圆杆一端装夹在传感器的标定装置上，此时的圆杆可视为一个变截面悬臂梁，圆杆的另一端拴一根细铜丝，细铜丝绕过安装在标定装置上的滑轮吊起砝码，通过剪断铜丝，突然释放砝码，使得圆杆做弯曲自由振动，采集应变信号并从中提取各阶应变模态的无阻尼自振频率和阻尼比。由于应变信号很微弱且易被噪声污染，经过调理(包括调零、约3万倍的放大和截止频率为318 Hz的低通滤波)之后仅能获得0.15 s的自由衰减响应信号(如图4所示)，信号的采样频率为2 000 Hz。由于信号的采样时长过短，不能直接使用基于连续小波变换的模态参数识别方法。

图3 具备力感知功能的微创外科手术机器手Fig.3 Minimally invasive surgery manipulator with force sensing ability

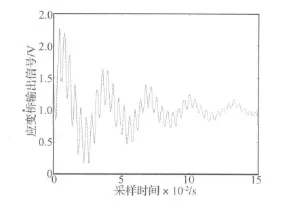
图4 调理后的应变桥输出信号Fig.4 Output of strain gauge bridge after signal conditioning

表4给出了对信号双向延拓后，应用连续小波变换对力传感器的应变模态参数进行辨识的结果(所用的反向传播神经网络如图1所示，参数与第3节数值仿真中所用的参数相同)，由于低通滤波器的限制，仅能辨识到前两阶应变模态。表4给出的辨识结果表征了力传感器的动态特性，为传感器的建模以及进一步设计补偿器提高传感器的动态响应速度提供了实验依据。当阻尼比较大时，自由衰减响应信号的衰减速度很快，而在实际信号中所包含噪声的幅度却不会以同样的规律衰减，这就导致有用信号逐渐被噪声淹没，本文提出的方法为这样一类问题提供了解决方案:将这部分受噪声污染较重的信号直接剔除，而后对信号进行双向延拓，延拓的信号比原信号具有较高的信噪比，从而能够更加准确地利用基于小波变换的方法估计模态参数。

表4 力传感器应变模态参数的辨识结果(fb=1，fc=2)Tab.4 Identified strain modal parameters of force sensor(fb=1，fc=2)

5 结论

考虑到人工神经网络具有自学习和自适应的能力，本文提出了一种基于连续小波变换和反向传播神经网络的模态参数辨识方法。利用反向传播神经网络对自由衰减响应信号的双向延拓，解决了小波变换的边界效应问题，扩展了传统模态参数辨识方法的应用领域。数值仿真以及对力传感器进行的动态特性测试实验表明，本文提出的方法在信号的采样时长很短时也能够准确地辨识各阶模态的阻尼比和无阻尼自振频率，实用性较强，并体现出一定的抗噪声能力。

［1］ Le T P，Argoul P.Continuous wavelet transform for modal identification using free decay response［J］.Journal of Sound and Vibration，2004，277(1-2):73-100.

［2］滕 军，朱焰煌，周 峰，等.基于复Morlet小波变换的大跨空间结构模态参数识别研究［J］.振动与冲击，2009，28(8):25-29.

［3］徐晓霞，任伟新，韩建刚.基于响应协方差小波变换和SVD的结构工作模态参数识别［J］.振动工程学报，2010，23(2):194-199.

［4］代 煜，孙和义，李慧鹏，等.基于小波变换的弱非线性阻尼和刚度辨识方法［J］.振动与冲击，2009，28(2):51-55.

［5］ Boltezar M，Slavic J.Enhancements to the continuous wavelet transform for damping identifications on short signals［J］.Mechanical Systems and Signal Processing，2004，18(5):1065-1076.

［6］伊廷华，李宏男，王国新.基于小波变换的结构模态参数识别［J］.振动工程学报，2006，19(1):51-56.

［7］徐增丙，轩建平，史铁林，等.LS-SVM在基于小波变换的模态分析中端部效应的应用［J］.中国机械工程，2008，19(13):1614-1620.

［8］Kijewski T，Kareem A.Wavelettransformsforsystem identification in civil engineering［J］.Computer-Aided Civil and Infrastructure Engineering，2003，18(5):339-355.

［9］Yan B F，Miyamoto A，Bruhwiler E.Wavelet transform-based modal parameter identification considering uncertainty［J］.Journal of Sound and Vibration，2006，291(1-2):285-301.

［10］ Delprat N，Escudie B，Guillemain P，et al.Asymptotic wavelet and gaboranalysis:extraction ofinstantaneous frequencies［J］.IEEE Transactions on Information Theory，1992，38(2):644-664.

［11］ Fredric M H，Ivica K.(著)，叶世伟，王海娟(译).神经计算原理［M］.北京:机械工业出版社，2007.

［12］ Yu K，Ye J，Zou J，et al.Missile flutter experiment and data analysis using wavelet transform ［J］.Journal of Sound and Vibration，2004，269(3-5):899-912.