广州新塔不同激励下动力特性监测

陈伟欢，吕中荣，陈树辉，倪一清，廖渭扬

(1.中山大学 应用力学与工程系，广州 510275;2.香港理工大学 土木及结构工程系，香港)

随着我国经济和建筑技术的发展，超高耸结构日益增多。如即将竣工并将在2010年广州亚运会投入使用的广州新电视塔，广州西塔以及即正在兴建的广州东塔和上海中心等，都属于超高耸结构。在动力特性方面，这类超高耸结构的第一阶振动频率很低，如广州新电视塔的第一阶振动频率不到0.1 Hz，属于高柔结构，对风荷载和长周期地震非常敏感，所以结构既要考虑抗震也要考虑抗风，近几年全球地震频繁，而广州市又地处台风带，夏季台风影响频繁，因此对广州新电视塔进行不同激励下的动力特性监测，动态的了解结构在日常使用环境下以及在强台风、地震等灾害性荷载下的结构性态，不仅可以进行极端灾害情况下的安全性预警，为业主进行灾害的应急管理提供决策依据，并且可为抗震减振设计提供宝贵的基础资料，为超高层建筑结构新技术的研究提供重要参考。本文作者已经对广州新电视塔台风期间的动力特性做了一些研究［1］。

广州新电视塔高610 m，是广州市新的地标性重点工程，如图1所示。其结构超高、形体奇特、结构复杂，在超高层建筑发展史上具有里程碑的意义。因此，在建造过程中的施工监控与运营期间的健康监测都具有十分重要的意义，一个包括超过700个传感器的长期结构健康监测系统已经广州新电视塔上运行［2］，而结构的动力特性测试正是监测内容的重要组成部分之一。

图1 广州新电视塔Fig.1 Canton Tower

以广州新电视塔为背景，介绍了其结构健康监测系统中的振动测试子系统。利用该子系统测得的不同激励下结构的加速度响应数据，首先，比较了在不同激励下结构的加速度时程响应和功率谱密度。然后，利用加速度响应数据进行模态分析并比较了在不同激励下结构的模态参数(包括频率、振型和阻尼比)。最后，利用希尔伯特-黄变换获得结构在不同激励下的瞬时频率和结构响应能量分布，并与小波变换的结果相比较。结果可为了解超高层建筑在不同激励下的动力特性提供参考。

1 振动测试系统

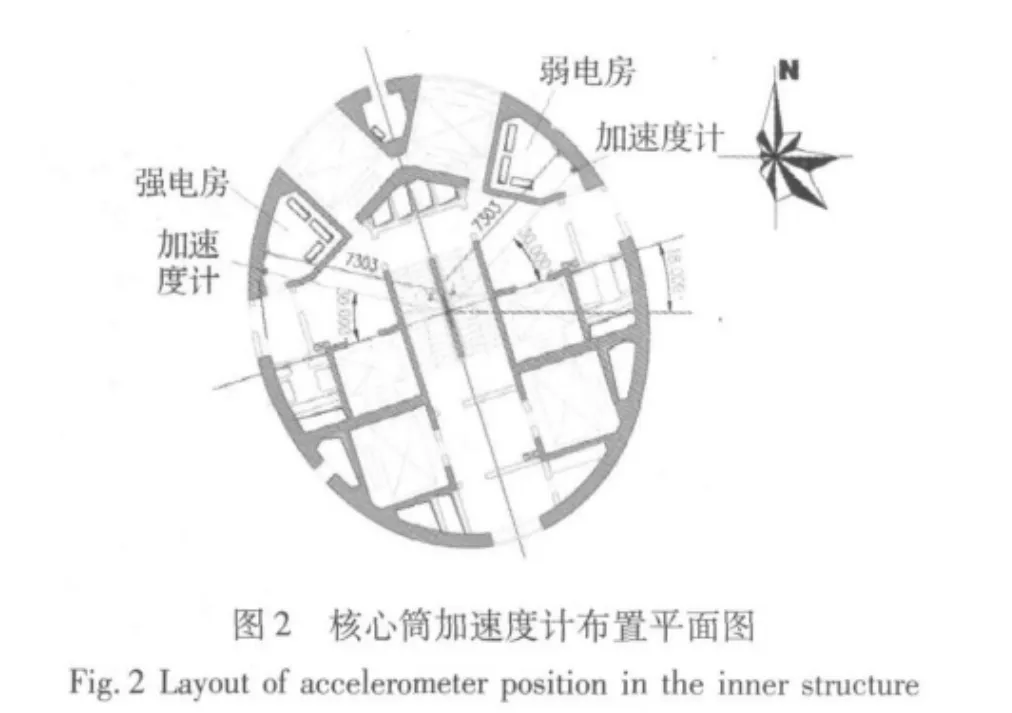
振动测试中加速度传感器全部布置在核心筒内8个监测断面上，其高程分别为 30.63 m、119.30 m、171.10 m、228.50 m、275.30 m、332.15 m、384.24 m 和446.80 m。除了截面 4(即 228.50 m)和截面 8(即446.80 m)布置4个加速度计外，其他每个截面上布置2个加速度计。每个截面的两个测点分别位于核心筒的强电房与弱电房里，其平面图如图2所示。

强电房的所有加速度传感器均布置为X方向(短轴方向)，弱电房的所有传感器均布置为Y方向(长轴方向)，第四和第八个截面每个测点在X方向和Y方向各布置一个加速度计。

数据采集系统采用分布式同步测量系统(如图3)，在8个测量截面的弱电房里各安置一个采集子站，用于采集该截面的加速度响应数据。8个子站用网络线连接起来。进行加速度信号采集时，采集系统通过发送一同步信号以达到各个采集子站同步采集的效果，最后将数据存储在PC机上。关于该振动测试系统更多详细资料可参考文献［3］。

由于能够自动连续的采集并存储数据，该振动测试系统已经成功的监测到多次地震或台风激励下广州新电视塔的结构动力特性。本文主要分析2009年12月19日台湾花莲地震，2009年9月15日台风巨爵及一般风荷载激励下结构的动力特性。

2 结构动力响应

广州塔在不同激励下的动力响应特性可简化认为是多自由结构的受迫振动，结构的动力响应特性与激励密切相关。不同激励荷载的显著频段不同，从而激发结构不同频段的模态频率。由于风脉动的频率非常低，所以结构在风荷载特别台风激励下一般表现出以最低几个频率的能量响应为主。地震激励的显著频率较风荷载高，一般为0.1 Hz到10 Hz不等，所以结构在地震激励下所表现出来的主要模态频率较风荷载激励下的要高。

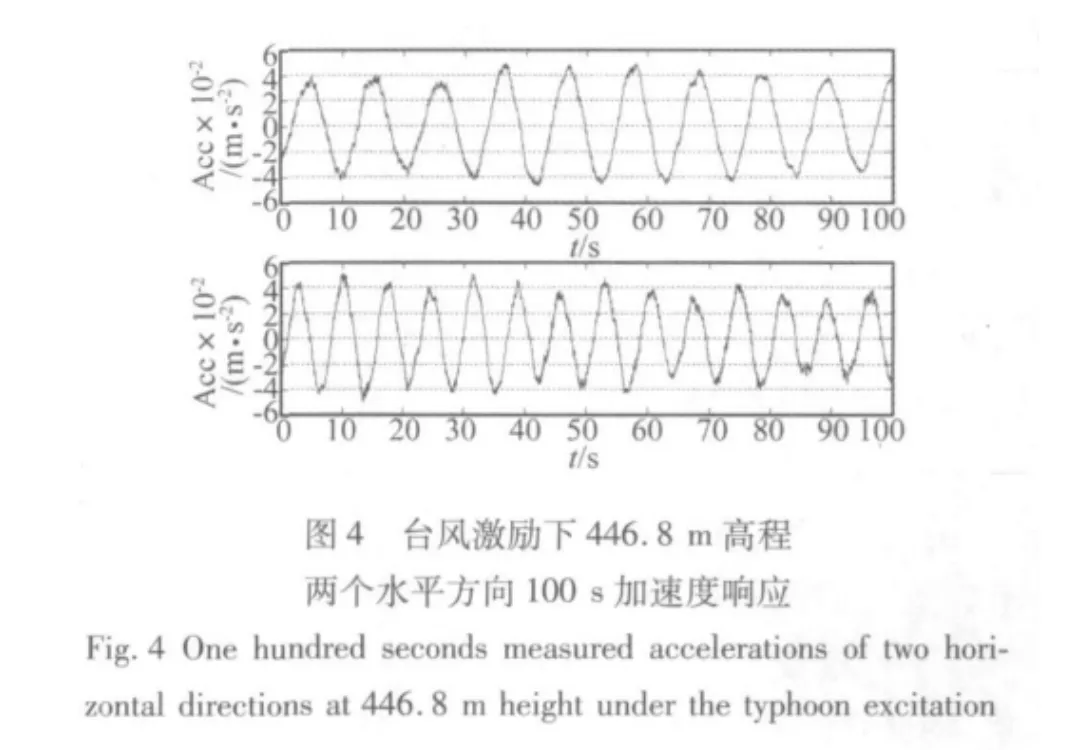
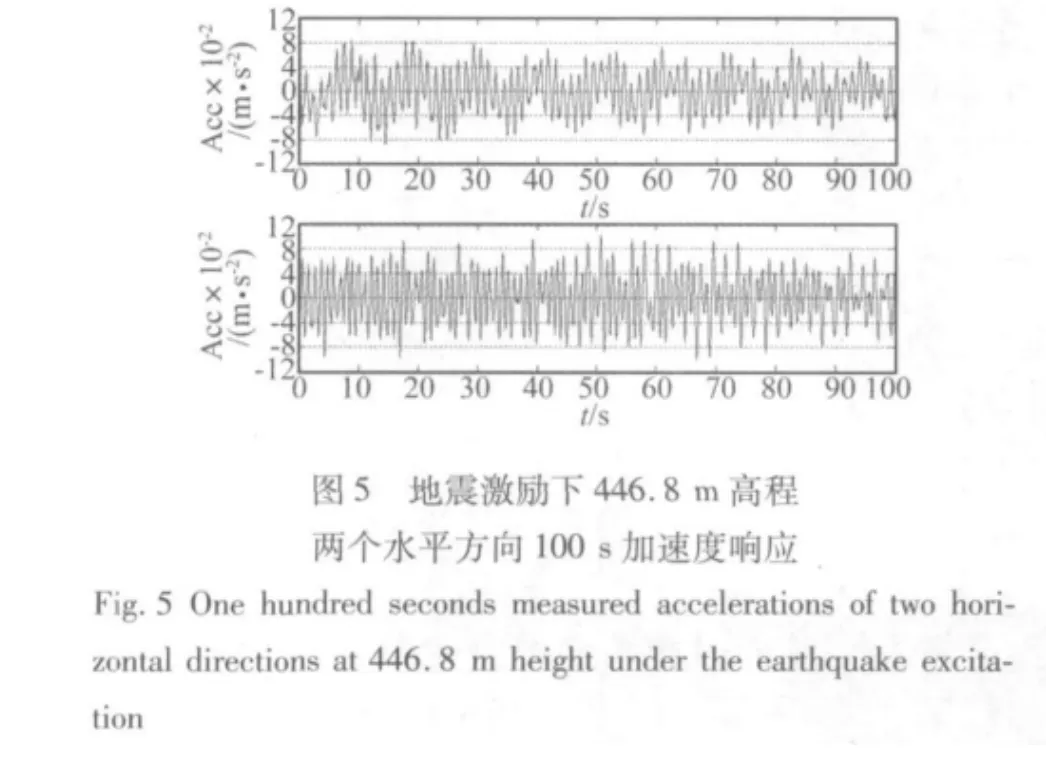
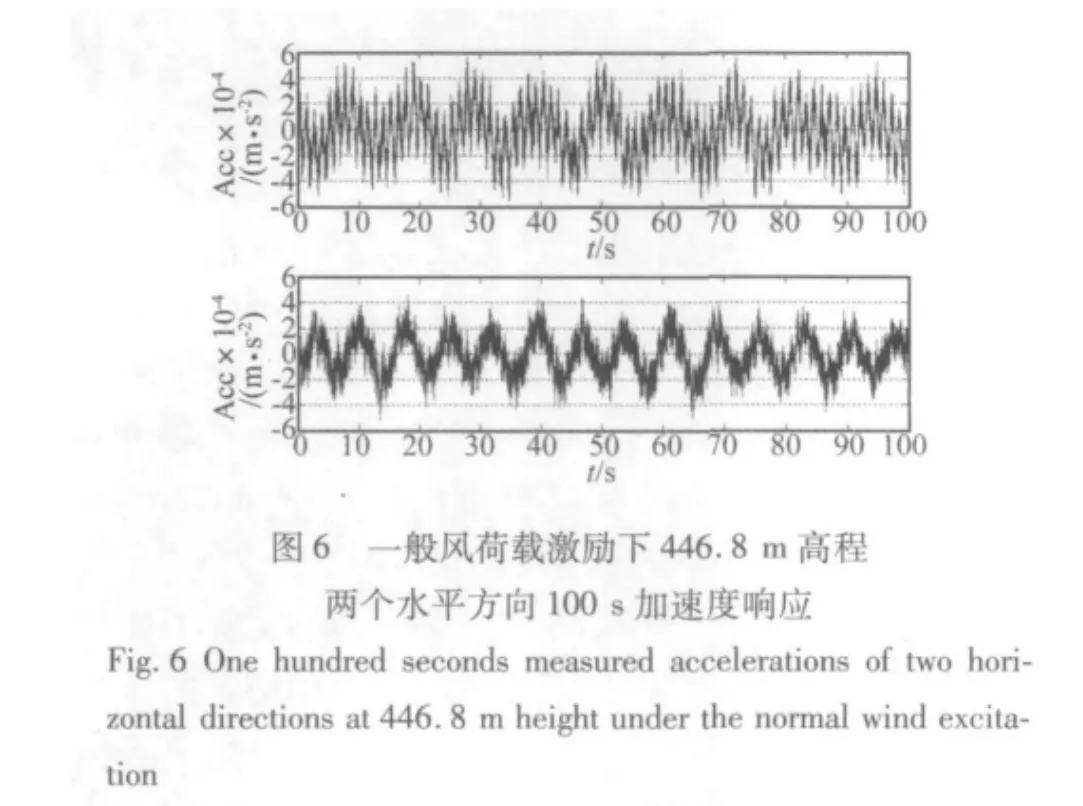
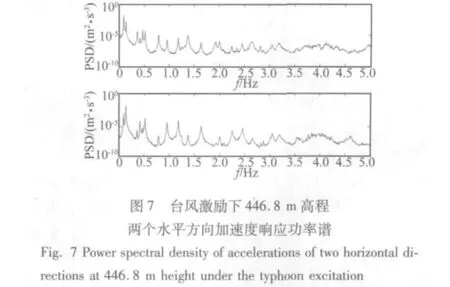
如图4至6分别展示了台风、地震和一般风荷载激励下446.8 m高程两个水平方向100 s的加速度响应。从这三个时程图上可以看到不同激励下结构的加速度响应有很大的不同。在台风激励下，结构的加速度响应大约为0.05 m/s2，前两阶的低频响应清晰可见，两个周期大约在0.1 Hz和0.14 Hz左右。在地震激励下，结构的响应频率要比在台风激励下的主要频率高的多，从时域上较难看清主要频率的精确大小，由于地震距离广州新电视塔较远，所以结构的响应并不是特别大，大约为0.01 m/s2。在一般风荷载激励，结构的响应较小，也是以低频为主，低频响应中夹杂着高频响应。

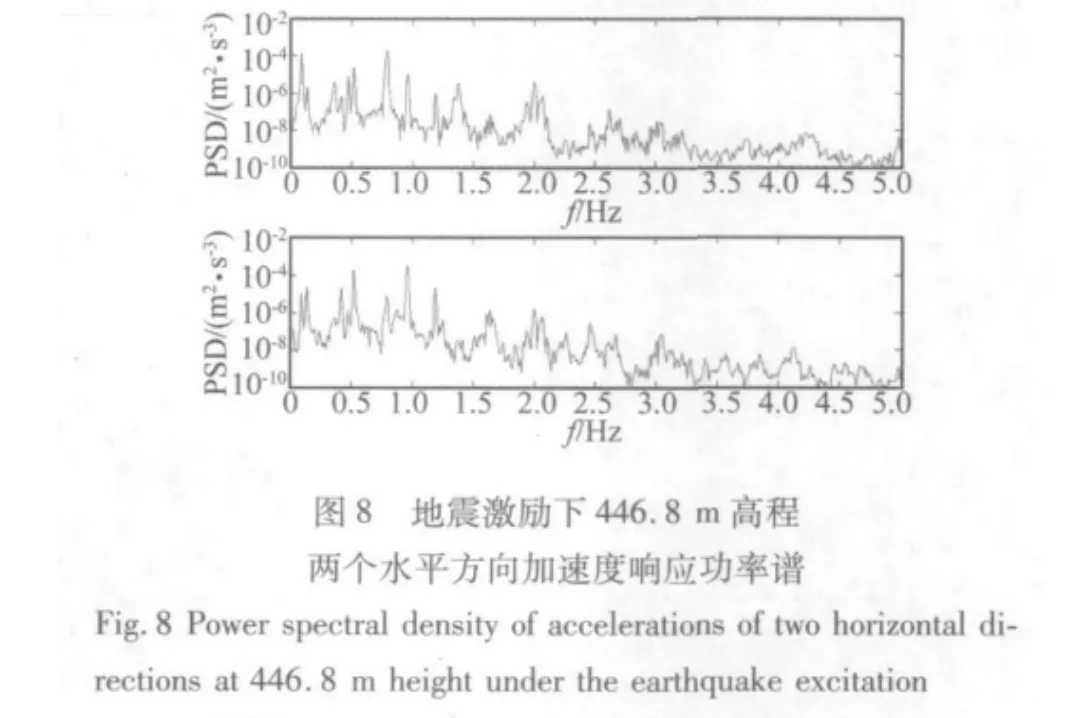
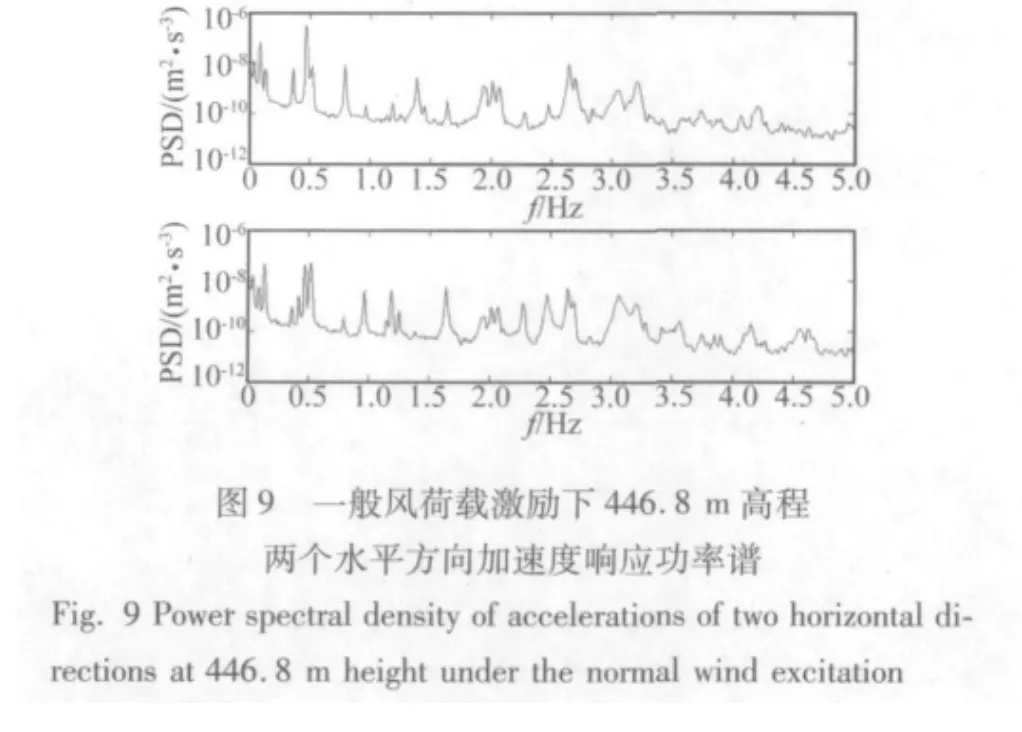
进一步分析数据，对加速度响应数据作平均功率谱密度估计，如图7至图9所示，结构在不同激励下都呈现出密频并且多模态耦合的形态，但是在不同激励下结构最显著的模态频率不同。在台风激励下，结构的加速度风振响应以最低两阶模态频率为主。在地震激励下，结构的加速度地震响应以0.8 Hz和1 Hz左右两个模态频率为主。在一般风荷载激励下，结构以较低几个模态频率为主。

3 模态分析

在过去的一段时间里，由于土木工程结构规模巨大无法采用人工激励，仅基于输出或者叫做基于环境振动的模态分析已经在结构健康监测得到广泛的应用。目前，国内外研究者提出了多种仅基于输出响应的模态参数识别方法。本文同时考虑算法的准确性和稳定可行性，最终采样频域分解法(Frequency domain decomposition)进行模态参数识别。

频域分解法［4］是峰值拾取法的延伸，克服了峰值拾取法的缺点，主要思想是:对响应的功率谱进行奇异值分解，将功率谱分解为对应多阶模态的一组单自由度系统功率谱。该方法识别精度高，有一定的抗干扰能力。已在一些大型土木结构的模态识别中成功应用［5-6］。

采用频域分解法，利用不同激励下结构的加速度响应，识别了不同激励下结构的模态参数。前十阶频率和阻尼比识别结果见表1。另外，图10还给出了前四阶归一化振型的比较。

从表1可以看出:① 不同激励下结构的频率略有不同，这可能与输入的激励有关，也可能与环境因素(如温度、湿度等)有关。但可以确定的是，实际结构的固有频率不是一成不变的，而是随着温度和激励的变化而略有变化。环境因素可以影响结构的刚度从而影响频率。并且实际结构存在非线性，非线性结构的振动频率受诸多因素(其中包括激励)影响，大型工程结构的随机非线性理论和研究方法目前尚未完善。②阻尼比的识别结果相差较大，这与阻尼比的复杂机制有关。③ 在一般风荷载激励下，结构第十阶模态很难识别出来。

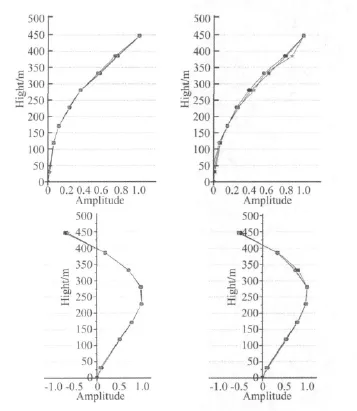
图10 不同激励下前四阶振型比较Fig.10 Compare the first four modes shape under different excitation condition

4 时频分析

时频分析方法因能同时在时域和频域内观察信号的演变，提供信号的局部时频特征，因而不仅能分析平稳信号且能分析非平稳信号。由于时频联合分析方法与传统的时域和频域分析方法相比具有不可比拟的优点，使其不仅在信号处理领域内得到了迅速的发展，而且在其他领域如土木工程领域也得到了广泛的应用［7］。土木工程中的地震工程、防灾减灾、结构抗震分析及健康监测等领域都会遇到非平稳信号的处理问题，因此，将信号处理中新的发展成果应用于土木工程中，极大地促进了该领域的发展。而在众多的时频分析方法中，小波变换和希尔伯特-黄变换(HHT)两种方法受到很大关注。

小波变换通过对母小波进行尺度伸缩和平移得到的子小波进行分解，在时间尺度域内分析信号的一种时频分析方法。小波变换克服了短时傅里叶变换固定时窗、恒定分辨率的限制，具有多分辨分析的性质。然而从本质上讲，小波变换是一种窗口可调的傅里叶变换［8］，摆脱不了傅里叶变换的局限，同样会存在能量泄露，受到不确定性原理的限制。本文分析采用目前最为广泛应用的Morlet小波。

Hilbert-Huang变换包括经验模式分解(EMD)和Hilbert变换两部分。在时域内将信号自适应地分解为多个在任意时刻只有单一振荡的内在模态函数(IMF)和一个剩余分量，并在分解过程中保持信号本身的特性，分解后对每个IMF进行Hilbert变换得到瞬时频率和瞬时幅值。经验模态分解基于瞬时频率的观点，打破了不确定性原理的限制，对信号的局部信息进行分析，因此得到的时频谱具有很高的时频分辨率［9］。作为一种新的方法，虽然已经成功应用于很多研究领域，但是仍然存在很多问题，如边界效应，模态分量之间不完全正交等［9］。对于结构的加速度信号分解，EMD无法分解密集的频率，即分解完的模态分量(IMF)含有多个实际模态频率在里面，从而造成所萃取的瞬时频率不规则。为克服这种现象，文献［10］提出了一种改进的HHT方法，该方法首先利用FFT和带通滤波器，将实际结构响应通过带通滤波器分解成多个窄带信号，最后再利用Hilbert变换把信号在时频域上展现出来。本文分析采用该改进的HHT法。

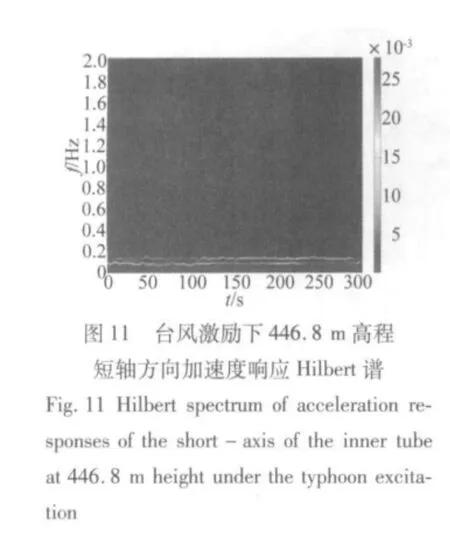
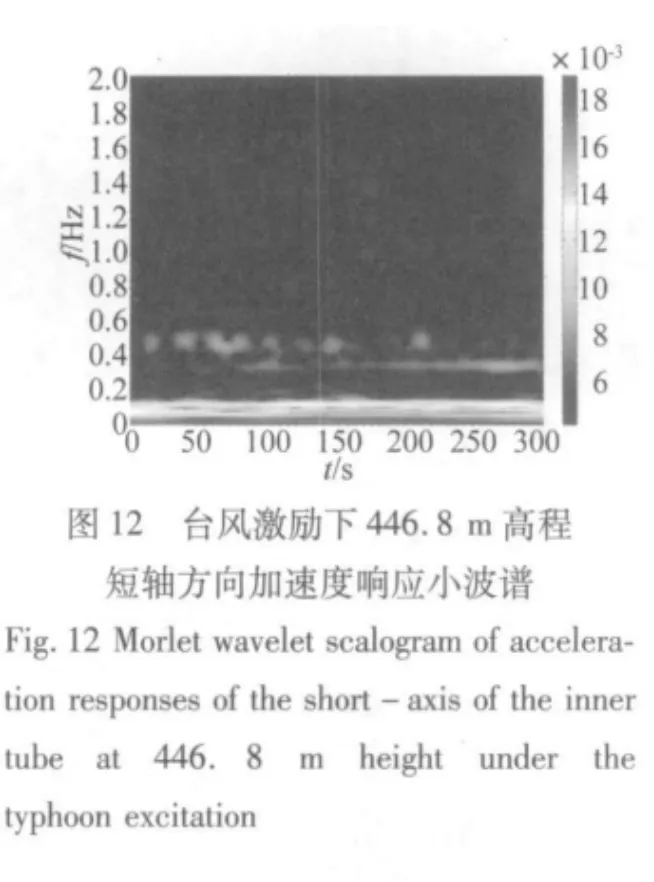
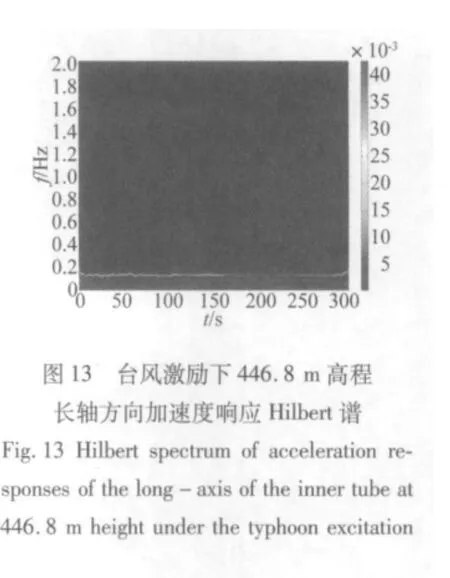
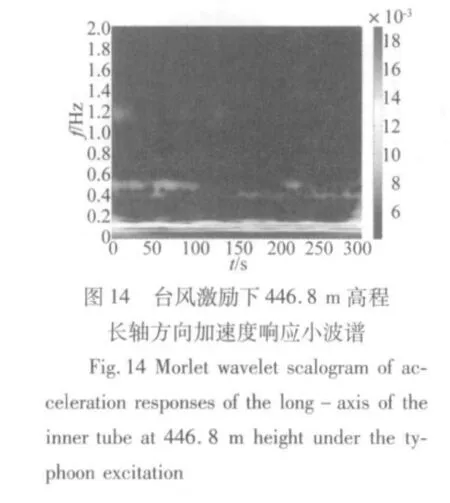
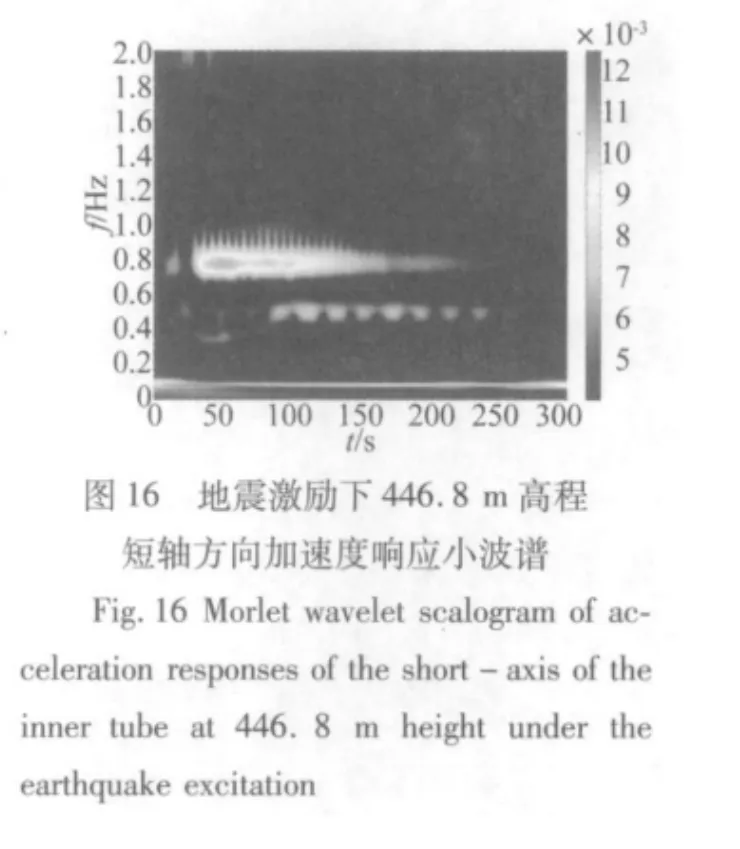
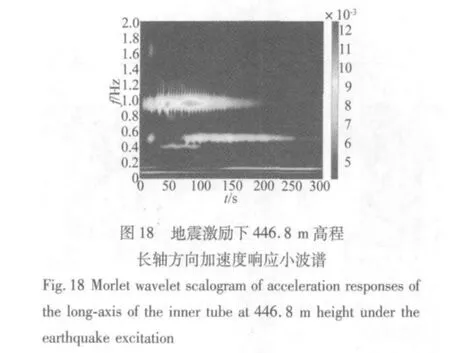
结构对不同时频特性的激励其响应特性是不同的。图12至图18所示为广州新电视塔446.8 m高程加速度响应在台风激励和地震激励下的Hilbert谱和小波谱。首先对比同个振动信号的Hilbert谱和小波谱，两者都能大致描述结构响应的能量随时间的变化情况，然而Hilbert谱能够很清晰的反应结构的瞬时频率随时间的变化，小波谱只能大概反映结构能量随时间的变化情况。进一步比较不同激励下结构能量随时间的变化情况，在台风激励下，结构的响应在时间上主要表现为最低的两个模态频率，而在地震激励下，结构的响应主要表现为0.8 Hz和1 Hz左右两个模态频率，并且随着地震激励的减弱而逐渐减弱，同时在0.5 Hz左右也有一些能量分布，在地震激励的同时结构也受一般风荷载的激励，所以结构在时间上还一直表现出最低0.1 Hz左右的模态频率。

表1 不同激励下模态频率和阻尼比识别结果比较Tab.1 Comparison of modal frequency and damping ratio under different excitation condition

5 结论

本文以广州塔为背景，介绍了其结构健康监测系统中的振动测试子系统，识别了结构在不同激励下的模态参数，并利用时频分析方法获得结构在不同激励下的动力特性，可以得到以下结论:

(1)不同激励下结构的模态参数略有不同，这可能与输入的激励有关，也可能与环境因素(如温度、湿度等)有关。

(2)结构在不同激励下都呈现出密频并且多模态耦合的形态，但是在不同激励下结构最显著的模态频率不同。在台风激励下，结构的加速度风振响应以最低两阶频率为主。在地震激励下，结构的加速度地震响应以0.8 Hz和1 Hz两个频率为主。在一般风荷载激励下，结构以较低几个频率为主。

(3)Hilbert谱和小波谱两者都能大致描述结构响应的能量随时间的变化情况，然而Hilbert谱能够很清晰的反应结构的瞬时频率随时间的变化，小波谱只能大概反映结构能量随时间的变化情况。

［1］陈伟欢，梁 硕，吕中荣，等.超高耸结构台风期间动力特性监测［J］.振动与冲击，2010，29(6):15-20.

［2］Ni Y Q，Xia Y，Liao W Y，et al.Technology innovation in developing the structuralhealth monitoring system for guangzhou new TV tower［J］.Structural Control and Health Monitoring，2009，16(1):73-98.

［3］ Xia Y，Ni Y Q，Ko J M，et al.ANCRiSST benchmark problem on structural health monitoring of high-rise slender structures-phase I:field vibration measurement［C］.Proceedings of the 5th International Workshop on Advanced Smart Materials and Smart Structures Technologies，USA，Boston，2009:30-31.

［4］Brincker R，Zhang L，Andersen P.Modal identification from ambient responses using frequency domain decomposition［C］.Proceedings of the 18th International Modal Analysis Conference，San Antonio，Texas，USA，2000，4062(2):625-630.

［5］ Gentile C，Saisi A.Ambient vibration testing of historic masonry towersforstructuralidentification and damage assessment［J］.Construction and Building Materials，2007，21(6):1311-1321.

［6］He X F，Moaveni B，Conte J P，et al.System identification of alfred zampa memorial bridge using dynamic field test data［J］.Journal of Structural Engineering，ASCE，2009，135(1):54-66.

［7］Li Q S，Wu J R.Time frequency analysis of typhoon effects on a 79-storey tall building［J］.Journal of Wind Engineering and Industrial Aerodynamics，2000，95(12):1648-1666.

［8］ Kijewski-Correa T，Kareem A.Efficacy of Hilbert and wavelet transforms for time-frequencyanalysis［J］.Journalof Engineering Mechanics，ASCE，2006，132(10):1037-1049.

［9］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis ［J］. Journal of Proceedings of the Royal Society of London Series A，1998，454(1971):903 995.

［10］ Yang W X.Interpretation of mechanical signals using an improved Hibert-Huang transform ［J］.Mechanical Systems and Signal Processing，2008，22(5):1061-1071.