微型燃气轮机浮环轴承-悬臂转子系统动力学特性分析

沈那伟，陈照波，焦映厚，马文生

(哈尔滨工业大学 机电学院，哈尔滨 150001)

浮环轴承-悬臂转子结构应用在微型高转速燃气轮机中具有结构紧凑、能效比高、便携性好等特点［1］。浮环轴承，其原理如图1所示，作为其支承部件具有独特的双油膜结构，提供了较好的阻尼特性和较大的承载力，具有稳定动力学行为。由于其价格低廉，使其可以替代滚动轴承及其他类型轴承。广泛用于高速、小型的旋转机械中，例如汽车发动机的涡轮增压器等［3-4］。

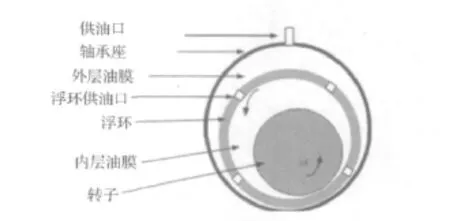
图1 浮环轴承原理图Fig.1 Floating ring bearing

早在20 世纪40 年代，Shaw 和 Nussdorfer［5］提出了浮环轴承的双层油膜的作用使其能有效地减少运行时的摩擦阻力从而降低工作温度。但是，由于浮环轴承的力学原理比普通圆柱轴承复杂的多，并且在试验和实际运行中呈现出复杂的油膜涡动、次同步振动和极限环运动现象，传统的润滑理论及线性稳定性理论对于浮环轴承-转子系统的动力学特性已经很难做出有效地解释并且不再适用［6-8］。近年来国内外许多学者对浮环轴承的特性进行了大量的计算及实验研究［9-10］，尤其 T＆M 大学的 Andres Luis等［10］总结了前人的经验，对浮环轴承-发动机涡轮增压器转子系统进行了较为深入的研究，并取得了阶段性成果。但是他们的研究仅限于轻载-对称哑铃型结构的转子系统。而相对于浮环轴承-重载悬臂转子系统的分析及其物理模型的理论分析和仿真，国内外鲜有记录。本文针对此转子结构支承的某微型燃气轮机的实际转子系统进行仿真和实验研究。根据流体力学润滑理论，推导出浮环轴承适用的Reynolds方程，利用四边形等参数h-有限元方法建立单元，通过Galerkin-加权余量法求解浮环轴承的双层油膜力Reynolds方程。用摄动法确定了浮环轴承双层油膜力在某一摄动下的等效刚度和阻尼系数。应用Timoshenko梁理论建立浮环轴承-悬壁转子系统的有限元分析模型，使用商业有限元分析软件Ansys12.1，对悬臂转子-浮环轴承系统进行转子动力学分析。并通过具体的实验比照，验证该物理模型的正确性。

1 浮环轴承的运动机理分析

分析浮环轴承-悬臂转子动力学问题的首要任务是对于浮环轴承的内外双层油膜的运动机理进行分析。如上文所述，许多学者对于浮环轴承的油膜特性进行了大量的理论和实验研究工作。浮环轴承由一个可以浮动的圆环嵌套在轴颈与轴承座之间，浮环的动力学性能分别由内、外层油膜hi，h0决定。

内层油膜的旋转引起浮环的转动，而外层油膜的摩擦应力作用又阻止浮环的转动，因此浮环受到的是两个相反的粘性剪切力的作用，以低于轴颈的旋转速度转动。其润滑力学原理如图2所示。

内、外油膜流体动力学压力分别由Pi、P0表示，其无量纲Reynolds方程如式(1)、式(2)所示:

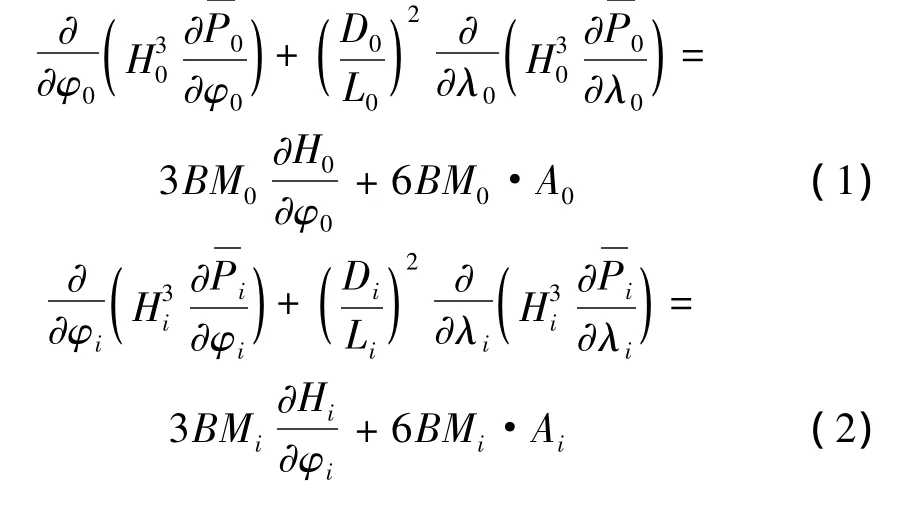
其中:

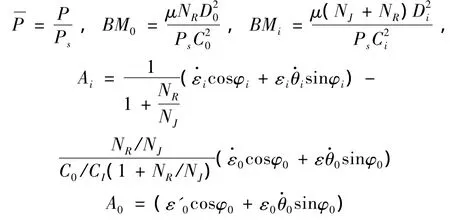
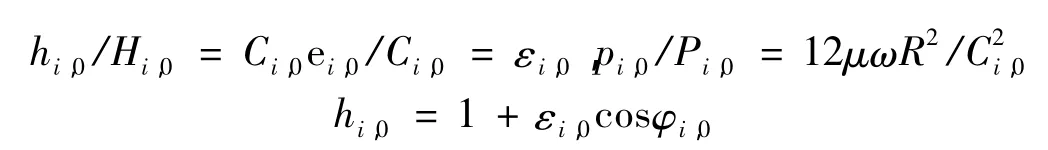
图2 浮环轴承流体润滑力学结构Fig.2 Coordinate system for description of FRB

采用h-精细有限元方法，对浮环内外表面进行网格划分，其边界条件如图3所示。单元类型为4节点等参单元，采用Galerkin-加权余量有限元法，也就是权函数代替基函数，令残差的权积分为零［11］，对浮环内、外表面油膜节点压力进行积分求解。

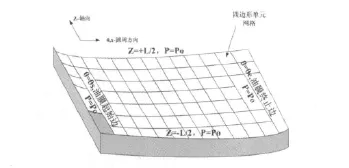
图3 浮环表面网格划分及压力分布边界条件Fig.3 Bushing surface pressure boundary conditions

即可求出整个有效区域内压力的分布情况，其详细过程暂略。求解出轴承的内、外层油膜力，代入浮环的运动方程中，由式(3)表示，内外油膜的摩擦力矩平衡平衡后环速比NR/NJ=0.3。

轴颈和浮环的微小摄动决定了内、外层油膜的刚度和阻尼系数。求解内、外层油膜的稳态压力后，其刚度和阻尼系统可以由式(4)-式(7)确定:

浮环轴承-悬臂转子系统由前后两个浮环轴支承，如图4所示。微型燃气轮机系统设计转速NJ=61 000 r/min，在20℃时，CD-40柴油机油的黏度系数μ=133 mm2/s标准供油压力Ps=558 kPa，以转子系统的前轴承为例，浮环轴承内、外层油膜的计算等效刚度和阻尼数值，如表1和表2所示。

表1 无量纲等效刚度和阻尼矩阵Tab.1 The equivalent stiffness coefficients matrix

浮环轴承重量为7.78×10-2kg，转子系统的重量为12 kg。外、内油膜间隙比Co/Ci=1.3，轴承长径比L/Do=0.52。

表2 无量纲等效阻尼矩阵Tab.2 The equivalent damping coefficients matrix

2 浮环轴承-悬臂转子系统的转子动力学分析

悬臂转子系统是非对称转子，与一般对称转子的转子动力学特性又很大的差异，由于质量在悬臂的一端，转子较长，转子的柔性大，所以旋转结构的陀螺效应对此结构转子的自然频率、临界转速等特性影响很大，陀螺效应的影响不能忽略［12］。所以在考虑哥氏力和陀螺力矩的情况下，利用Timoshenko梁单元理论建立浮环轴承-悬臂转子系统有限元模型能更好地分析此微型燃气轮机转子系统，如图4所示，其控制方程为［13］:

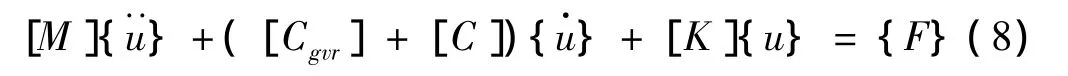
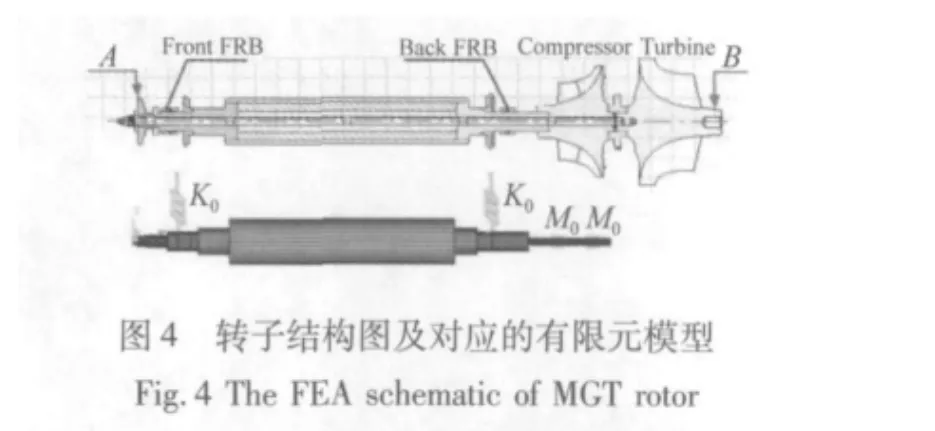
用商用有限元软件Ansys12.1建立浮环轴承-悬臂转子有限元模型。压缩叶轮和透平叶轮的质量作为集总质量加载在有限元结构中并且设置为隐藏，前后轴承载荷分别为34.3 N，127.4 N转子的长度是642.3 mm，加上悬臂段叶轮共计747 mm。敲击测试在实验转子上操作。如图5所示，一只加速度传感器分别布置在转子一端中心使其固定，另一只使其随转子自由游动。实验的测试结果为一阶自由-自由模态频率为382 Hz，其有限元仿真自由-自由模态频率为373 Hz，所以有限元模型的建立基本正确。浮环轴承-悬臂转子的坎贝尔图，如图6所示。图中信息包括各阶临界转速，阻尼振动频率和各阶振动模态。可见由于陀螺效应得影响，悬臂质量大和转子大柔性的原因，机器启动时刻，前几阶刚体横向模态频率比较接近。前五阶模态是横向刚体模态，随着转速的逐渐升高，第7阶是圆锥刚体模态，所对应的临界转速是18 416 r/min。较为危险的弯曲模态临界转速远高于实际运行转速，可以看出系统在超过圆锥模态临界转速后运行是安全的。

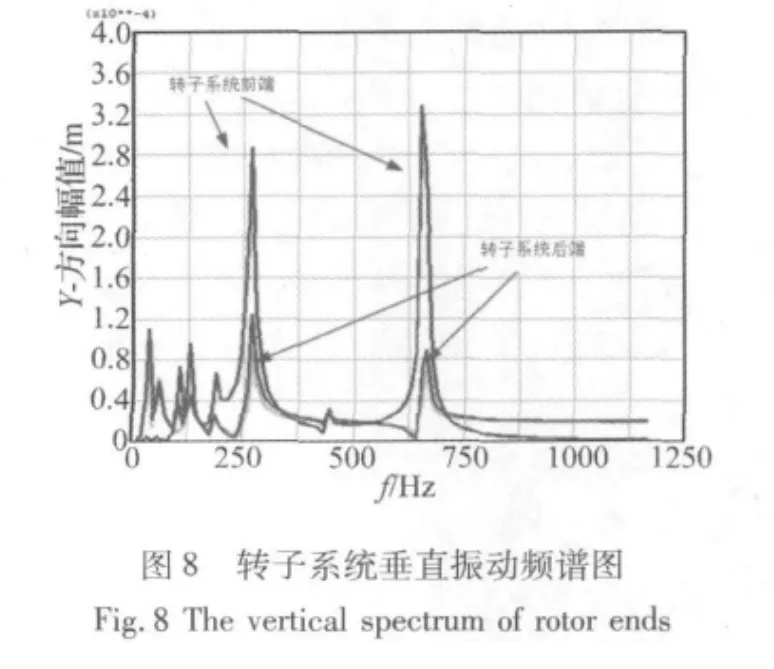
此外，系统的对数衰减率，如图7所示。前六阶刚体模态的对数衰减率由零趋向负值，说明起始时刻也就是转速在18 416 r/min之前系统是不稳定的，由于浮环轴承-悬臂转子的陀螺效应和悬臂质量造成系统失稳。第七阶模态后，转子系统是稳定的，也就是转子系统转速在超过18 416 r/min之后，但是在40 000 r/min附近系统又一次失稳，其原因随着阻尼的增大，转子柔性增强，叶轮端不平衡量造成剧烈振动引起的。图8-图10是系统谐响应频谱图和在665 Hz时，转子系统的不平衡响应。

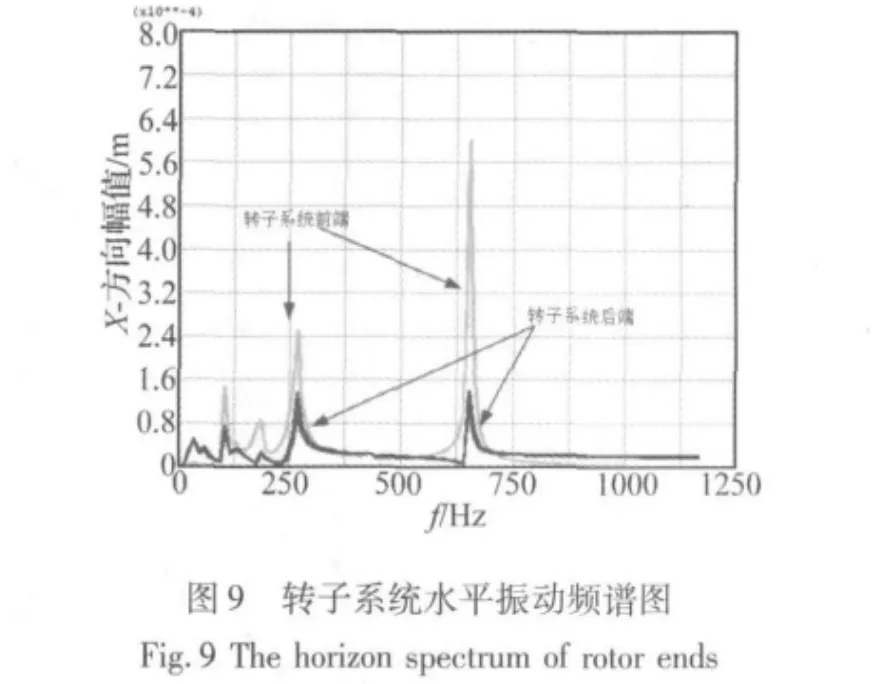
图8和图9表示浮环轴承-悬臂转子系统垂直和水平幅值-频谱图。可以看出同步振动的最大幅值对应的频率为665 Hz(39 900 r/min)，也就是失稳转速。而幅值较大的振动在频率也同样出现在290 Hz(17 400 r/min)，这是刚体圆锥模态临界转速点。与Compbell图预测得结果一致。因此其涡动比为0.437。图10描述了频率为665 Hz时的不平衡响应。它表明在前端浮环轴承附近水平和垂直振动比后端轴承剧烈，可能是由于陀螺效应引起的后端悬臂质量滞后于转子前段引起的。综合来看，整个转子系统的振动响应以低频或同步振动为主。

3 浮环轴承-悬臂转子系统试验研究

浮环轴承-悬臂转子系统设计转速是61 000 r/min。一对十字型放置的电涡流传感器分别安装在系统的前、后端。光电传感器安装在轴承座上指向浮环轴承。布尔登压力仪、流量计和热电偶记录系统润滑油CD40的压力、温度和流量。转子的润滑系统用油泵供油，工作转速80 kr/min的ABB变频电机用来驱动转子系统。一旦转子系统的振动幅值超过界限值，系统将立即被迫停机。

测试中，由于悬臂的支承结构和浮环轴承的双层油膜力的作用，使得整个转子系统产生了与其它系统不同的独特现象。

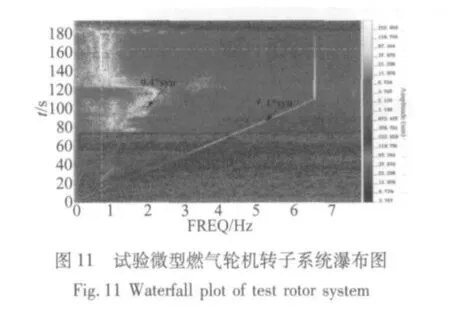
图10表示的是系统的瀑布图，图11所示是系统A端测量值的垂直振动频谱图，它们说明在系统工作工程中，存在一个低频振动成份不随转速的变化而变化。这个振动就是由浮环轴承的非线性双层油膜力的作用，引起的油膜涡动和振荡现象。测试的涡动比为0.4左右，这和数值计算结果比数值预测偏低，主要是因为线性有限元数值仿真不能预测到到失稳转速之后，由于油膜作用引起的油膜低频振动现象。

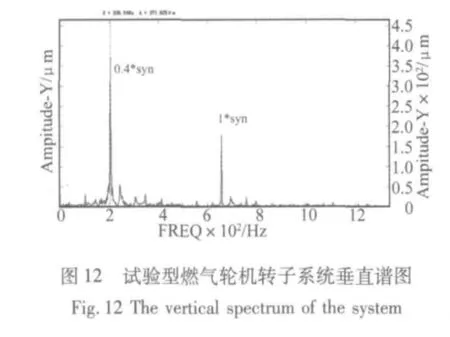
从整体分析可以看出，有限元预测的低频振动的幅值比试验转子的幅值略低，也是由于浮环轴承的非线性油膜力作用的影响。从图12可以看出除了有0.4倍低频振动的成分之外，还存在着少量低于0.4的成分这也是随着转速的升高，陀螺效应和非线性油膜力双重作用的结果。

4 结论

浮环轴承-悬臂转子支承系统广泛应用于分布式能源旋转机械中，对于能源紧缺的今天，微型燃气轮机具有广阔的发展前景。本文应用h-有限元方法求解浮环轴承的双层油膜力，利用摄动方法，在不同的偏心位置下，对浮环轴承的动态等效刚度和阻尼系数进行准确地求解。力求更精确地对于实际浮环轴承-悬臂转子进行分析。

其次，对浮环轴承-悬臂转子系统进行结构有限元转子动力学分析，利用Timoshenko梁理论，建立有限元模型，在商用有限元软件Ansys12.1，在考虑陀螺效应影响下，对浮环轴承-悬臂转子系统的临界转速、阻尼模态、动力学响应和稳定性进行分析预测，并与实验进行了有效的对比。

实验结果表明表明浮环轴承-悬臂转子支承系统从启动开始到60kr/min过程中存在多种非稳定的频率成份，其中包括启动时的陀螺效应影响，浮环轴承双层非线性有膜力产生了油膜低频涡动，并且有效的涡动比在0.4附近，浮环轴承-悬臂转子系统的独特的动力学行为是由长柔性悬臂，和不平衡质量的陀螺效应所引起。同时，试验也验证了利用商业有限元软件Ansys12.1的转子动力学功能可以快速比较准确地模拟浮环轴承-悬臂转子系统的转子动力学行为，为今后高速旋转机械的发展提供有利的条件。

［1］ Pilavachi P A，Mini.Micro gas turbines for combined heat and power［J］.Applied Thermal Engineering，2002(18):2003-2014.

［2］Craig P.The capstone turbogenerator as an alternative power sourse［J］.SAE，1997.

［3］沈那伟，陈照波，焦映厚.半浮环轴承支承100 kW微型燃气轮机转子-轴承系统非线性动力学分析［J］.振动与冲击，2008:117-119.

［4］Li C.Dynamics of rotor bearing systems supported by floating ring bearings［J］.Journal of Lubrication Technology，1982，104:469-477.

［5］ Shaw M C，Nussdorfer T J.An analysis of the full-floating journal bearing［J］ .Report No.866，National Advisory Committee for Aeronautics(NACA)，1947.

［6］Tanaka M，Hori Y.Stability characteristics of floating bush bearings［J］.ASME Journal of Lubrication Technology，1972，94:248-259.

［7］Rohde S M，Ezzat H A.Analysis of dynamically loaded floating-ring bearings for automotive applications［J］.ASME Journal of Lubrication Technology，1980，102:271-277.

［8］Li C H，Rhode S M.On the steady state and dynamic performance characteristics of floating ring bearings［J］.ASME Journal of Lubrication Technology，1981，103:389-397.

［9］康召辉，任兴民，王 鸷，等.浮环轴承系统中浮动环涡动运动研究［J］.振动与冲击，2010，29(8):195-197.

［10］ Holt C，San Andrés L，Sahay S，et al.Test response and nonlinear analysis of a turbocharger supported on floating ring bearings［J］.ASME J.Vibr.Acoust，2005，127:107-212.

［11］ Zienkiewicz O C，Taylor R L.The Finite Element Method(Six Edition)［M］.Published by Elsevier，2005.

［12］ Vance J，Zeidan F.Machinery vibration and rotordynamics［M］.John Wiley＆ Sons Inc，2010.

［13］ Nelson，Vaugh M.The dynamics of rotor-bearing systems using finite elements［J］.May Journal of Engineering for Industry，1976，98(2):593-600.