炭化层对粒子反弹系数测量实验研究*

徐义华,胡春波,李 江

(1西北工业大学固体火箭发动机燃烧、热结构与内流场国防科技实验室,西安 710072;2南昌航空大学,南昌 330063)

0 引言

固体火箭发动机广泛使用高含铝量的推进剂,燃气中含有大量的凝相粒子,粒子对绝热材料侵蚀的作用不容忽视[2-6]。研究粒子对绝热层侵蚀时,要预测粒子的运动轨迹。由于固体火箭发动机工作在高温高压环境,其粒子速度和粒子轨迹难以用实验测定,一般由数值计算进行预测。在数值计算中把粒子一般视为球形粒子,并对粒子与壁面(绝热材料的炭化层表面)的相互作用处理为反弹边界条件[2,5]。因此,炭化层对粒子的反弹系数是固体火箭发动机中两相流场计算的一个重要参数。如文献[2]使用多相N-S方程对TITANⅣ固体火箭发动机在推进剂燃后17.5in的几何形腔进行三维两相流场模拟时,对粒子与壁面作用采用了反弹边界条件,并取反弹系数为0.5。文献[5]在发动机三维两相流场计算中,对粒子与壁面的作用也采用了反弹边界条件,并取反弹系数为0.7。以上文献对反弹系数的取值未做说明,因此,一个合适的炭化层壁面反弹系数对数值计算是必须的。

文中应用模拟固体火箭发动机烧蚀环境的炭化层制样装置制备EPDM绝热材料炭化层,设计了一套粒子撞击炭化层装置,在粒子撞击炭化层过程中,应用高速摄影系统进行过程拍摄,对所得的图像进行处理来测量粒子撞击炭化层前、后速度和角度,从而计算出不同侵蚀角度下的炭化层反弹系数,建立炭化层反弹系数与粒子入侵角度的关系,为粒子对绝热材料的侵蚀力的计算及固体火箭发动机两相流动计算提供参考。

1 粒子撞击反弹模型

应用弹性理论Maw等人[7]建立了斜撞击反弹模型。Thornton 等人[8-11]对粒子碰撞壁面应用有限差分及有限元法进行了分析,更进一步证明Maw等人提出的粒子碰撞反弹模型。文献[12-14]分别对粒子撞击壁面及粒子与粒子碰撞的特性进行的测量结果证明了壁面对粒子反弹与入射角有关。

粒子撞击壁面过程如图1所示,粒子以速度V i、入射角θi撞击壁面后,以反弹角θr、线速度V r和旋转角速度ωr反弹。法向和切向反弹系数分别定义为:

图1 粒子撞出壁面反弹示意图

在粒子撞击壁面时,受到法向与切向的冲量作用,定义切向与法向的冲量之比f为:

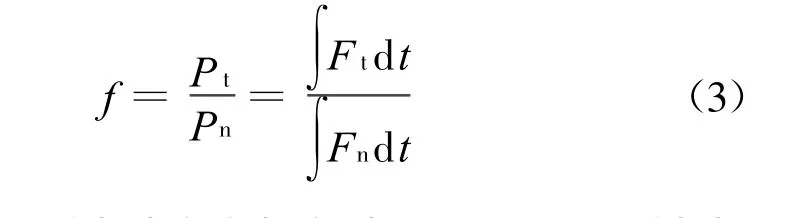
式中:P n、P t分别为法向和切向冲量;F n、F t分别为粒子接触壁面时的法向和切向分力。当粒子撞击壁面有滑移发生时,则 f=μ。

根据牛顿定律可得:

其中,m为粒子质量。由式(1)～式(5)可得粒子切向反弹系数与库仑摩擦系数、法向反弹系及侵蚀入射角的关系为:

同样,由转动冲量Pω可得:

式中:I为粒子转动惯量,ωi为粒子入射时的转动角速度 ωi=0。又因为:

其中,R为粒子的半径,根据式(4)、式(7)、式(8)可得:

对于球形粒子I=2mR2/5,因此:

将式(6)代入式(10)得粒子反弹后的转动角速度与库仑摩擦系数、法向反弹系数、粒子半径、粒子入射速度及侵蚀入射角的关系为:

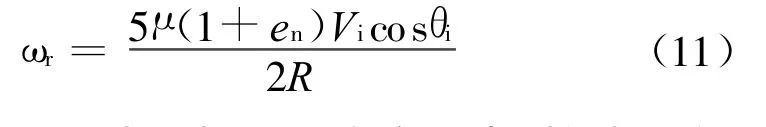
从以上模型可以看出,只要在实验中测得粒子的入射速度V i、入射角θi、反弹速度V r及反弹角θr,即可以得出粒子侵蚀炭化层的反弹特性。

2 测试系统及方法

根据粒子撞击壁面的反弹模型,为了测得粒子的入射速度Vi、入射角θi、反弹速度Vr及反弹角θr,建立的测试系统如图2所示,主要由光路成像系统、粒子弹射侵蚀装置、高速摄影机及高速摄影控制系统组成。其中,粒子弹射侵蚀装置主要由气缸、活塞、杯体、活塞挡盖、弹性胶垫、气源接头和炭化层夹具组成。粒子弹射侵蚀装置设计原理是应用高压气源推动活塞,可存放粒子的杯体与活塞固定连接,高速的活塞在缸体出口处撞击挡盖而停止,粒子则在惯性的作用下高速飞出撞击炭化层,固定炭化层的夹具角度可调,从而使粒子以不同的入射角侵蚀炭化层。

粒子撞击炭化层的过程,经光路成像到高速摄影仪的接收屏上。通过调节高速摄影仪的采样频率,将粒子侵蚀炭化层的入射及反弹过程以系列图像形式存储到计算机中。对所得的图像系列进行处理,可求得粒子入射速度V i、入射角θi、反弹速度V r及反弹角θr。

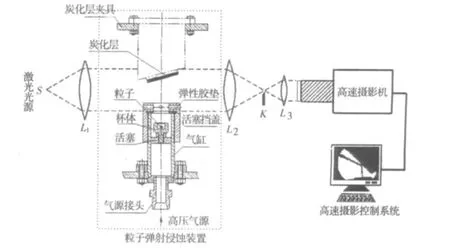
图2 测试系统原理图

3 图像处理方法

调节高速摄影仪采样频率为5000帧/s,粒子弹射装置将粒子从杯体弹出后,高速摄影记录了粒子在入射和反弹的全过程,图3为粒子入射过程图像。图4为粒子反弹过程的图像。

将记录到的粒子入射与反弹过程的图像叠加后可得到粒子在入射与反弹的全过程轨迹图,根据粒子轨迹可计算得到粒子的入射角与反弹角,并根据粒子入射和反弹时的帧数及距离可计算得到粒子的入射速度与反弹速度。如图5所示,粒子从杯体出口至侵蚀面的距离为 20.59mm, 历时为11/5000s,则其速度为v p1=9.36m/s,反弹时在6帧内经过路程为8.8mm,则其反弹速度为 7.33m/s,根据轨迹线可测得入射角为55°,反弹角为68°。

图5 粒子轨迹图

4 实验结果与分析

在固体火箭发动机动中,粒子在聚集状态下直径分布在5 ～ 200μm,线性平均粒度为 43.68μm[15]。在实验中直接应用接近发动机中的粒径大小的粒子进行侵蚀反弹试验,易受环境干扰,成像难度较大,且在固体火箭发动机中粒子对绝热材料的炭化层侵蚀作用主要为聚集后的粒子流。因此,为了体现粒子对炭化层的宏观侵蚀效应,实验选取了撞击炭化层的粒子直径为1.5mm。实验中在各侵蚀角度下,得到的炭化层法向反弹系数en和切向的反弹系数et见表1。

根据粒子撞击壁面反弹模型可计算出各侵蚀角度下的炭化层对粒子作用的摩擦系数μ,以及粒子反弹后的转动角速度ωr。从实验结果可以看出,炭化层对粒子反弹系数随着粒子的侵蚀角度而变化,对实验结果应用准牛顿优化算法进行三次方多项式拟合得到法向反弹系数和切向反弹系数随侵蚀角的变化关系式分别:

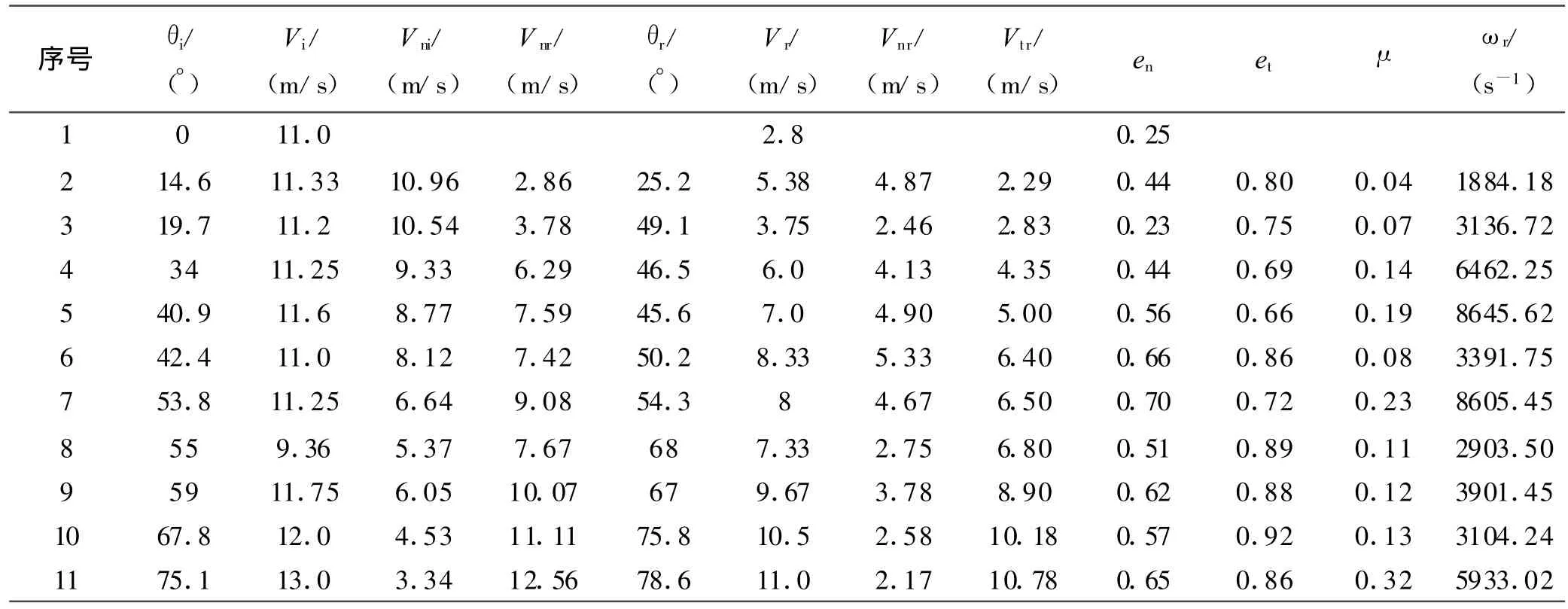
表1 各侵蚀角度下实验测量结果

由拟合式及实验结果给出炭化层法向和切向反弹系数随侵蚀角变化规律如图6所示,由图可知,法向反弹系数分布在0.2～0.7之间,在侵蚀角小于60°下随侵蚀角增大而增大,大于60°时随侵蚀角增大而减小;切向反弹系数分布在0.6～0.9之间,侵蚀角在0°～ 42°之间随侵蚀角增大而减小,在42°～70°之间随侵蚀角增大而增大,大于70°时,有下降趋势。

图6 炭化层反弹系数随侵蚀角变化规律

5 结论

1)建立的测量粒子侵蚀炭化层反弹系数的实验系统,可得到清晰的粒子撞击炭化层及反弹过程的系列图像。

2)炭化层对粒子的法向反弹系数分布在0.2～0.7之间,在侵蚀角小于60°下随侵蚀角增大而增大,大于60°时随侵蚀角增大而减小。

3)炭化层对粒子的切向反弹系数分布在0.6～0.9之间,侵蚀角在0°～42°之间随侵蚀角增大而减小,在 42°～70°之间随侵蚀角增大而增大,大于 70°时,有下降趋势。

4)在固体火箭发动机两相流场计算中,根据不同的粒子侵蚀角,应用式(13)、式(14)可得出不同的法向及切向反弹系数。

[1] 赵晓莉,岳红,张兴航,等.三元乙丙橡胶绝热层耐烧蚀性能的研究评述[J].材料科学与工程学报,2005,23(2):310-312.

[2] J S Sabnis,R K Madabhushi.Simulation of flow and particle impingement patterns in titanⅣSRM Aft closure[C]//31th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,July 10-12,1995/San Diego,CA.

[3] H Wirzberger,S yaniv.Prediction of erosion in a solid rocket motor by alumina particles[C]//41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit,July 10-13 2005,Tucson,Arizona.

[4] C Derbdge,C Powars.Acceleration effects on internal insulation erosion[C]//29th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,June 28-30,1993/monterey,CA.

[5] 李江,何国强,秦飞,等.高过载条件下绝热层烧蚀实验方法研究(Ⅰ)方案论证及数值模拟[J].推进技术,2003,24(4):315-318.

[6] 李江,何国强,秦飞,等.高过载条件下绝热层烧蚀实验方法研究(Ⅱ)收缩管聚集法[J].推进技术,2004,25(3):176-178.

[7] N Maw,JR Barber,JN Fawcett.Theoblique impact of elastic spheres[J].Wear,1976,38(1):101-114.

[8] C Thornton,K K Yin.Impact of elastic spheres with and without adhesion[J].Powder Technology,1991,65(1/3):153-166.

[9] C Thornton.Coefficient of restitutionfor collinear collisions of elastic-perfectly plastic spheres[J].Journal of Applied Mechanics,1997,64(2):383-386.

[10] C Thornton.Numerical Simulations of Discrete Particle Systems[J].Powder Technology,2000,109(1/3)Special Issue:1-298.

[11] C Y Wu,C Thornton,L Y Li.Coefficients of restitution for elastoplastic oblique impacts[J].Advanced Powder Technology,2003,14(4):435-448.

[12] D A Gorham,A H Kharaz.Themeasurement of particle rebound characteristics[J].Powder Technology,2000,112(3):193-202.

[13] M Sommerfelda,N Huber.Experimental analysis and modeling of particle-wall collisions[J].International Journal of Multiphase Flow,1999,25(6/7):1457-1489.

[14] M C van Beek,C C M Rindt,et al.Rebound characteristics for 50-μm particles impacting apowdery deposit[J].Powder Technology,2006,165(2):53-64.

[15] 刘洋,何国强,李江,等.聚集状态下凝相颗粒的收集与测量[J].推进技术,2005,26(5):477-480.