弹载捷联惯导系统的在线标定方法*

周本川,程向红,陆 源

(东南大学仪器科学与工程学院,南京 210096)

0 引言

弹载捷联惯导系统的误差主要来源于陀螺仪和加速度计的零位误差、标定因数误差和安装误差。一般情况下,转台标定补偿后若不重新拆装,安装角基本保持不变,但零位和标定因数存在随机启动不确定性误差,特别是随着库存时间的增长,相对转台标定值将产生很大差异。传统做法需要定期进行系统重新标定,费时费力。因此,应用滤波技术对传感器误差进行在线标定对于提高系统精度具有重要的应用价值。文献[1]和文献[2]应用Kalman滤波技术分别采用速度匹配和“位置+速度”匹配实现了传感器误差的在线标定。

在弹载捷联惯导系统在线标定的实际应用中,如果挠曲变形、杆臂等建模不准或者环境干扰较大,存在Kalman滤波性能恶化的问题。同时,在线标定的另一个关键问题是主子惯导系统的时间延迟问题。子惯导系统的滤波器接收到的主惯导信息存在大概40～120ms的时间延迟[3],时间延迟引起的误差降低了基准信息的精度,影响滤波估计效果,从而影响在线标定精度。目前,时间同步方法主要有硬件方法[4-5]和软件方法[6-7]。硬件方法需要专用的硬件电路,在一定程度上增加了系统的成本和复杂性。软件方法通过补偿时间延迟实现时间同步,文献[6]将时间延迟作为卡尔曼滤波器的状态变量对其进行滤波估计补偿,文献[7]给出了基于拉格朗日插值的同步方法,外推阶数越大,计算量越大,而且当时间延迟较大时,外推精度难以满足应用要求。

针对上述问题,文中首先建立基于“速度+姿态”匹配的在线标定H∞滤波模型,然后在分析时间延迟对H∞滤波估计影响的基础上进行软件方法补偿,最后通过机载试验数据的半物理试验加以验证。

1 在线标定滤波模型建立

1.1 状态方程

应用H∞滤波技术在线估计传感器的误差项,考虑到采用“速度+姿态”匹配方式,定义系统状态如下:

其中 :δV e 和 δV n 分别为东向和北向速度误差;φe、φn和φu分别为东向、北向和天向失准角;φx、φy和φz分别为子惯导系统相对主惯导系统的x向、y向和z向安装误差角;x和 y分别为x向和y向加速度计的常值偏置;εx、εy和εz分别为x向、y向和z向陀螺的常值漂移 ;δKx、δKy和δKz分别为 x 向、y向和z 向陀螺的标度因数误差。

根据子惯导系统的误差方程[8]可以得到在线标定的系统状态模型:

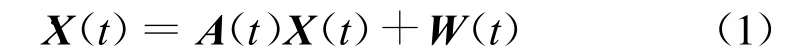
式中:A(t)为状态矩阵,W(t)为系统噪声。

1.2 观测方程

采用“速度+姿态”匹配的观测量为:

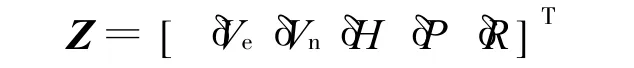
其中,δH、δP和δR分别为子惯导系统的航向角误差、纵摇角误差和横摇角误差。

根据主子惯导系统的速度和姿态输出差值[9]可以得到系统观测模型:

式中:H(t)为观测矩阵,V(t)为观测噪声。

对式(1)和式(2)进行离散化,即得到离散的在线标定滤波模型:

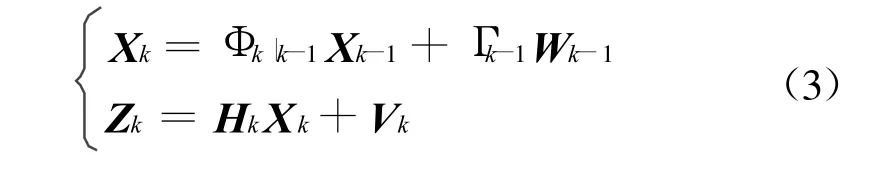
2 时间延迟分析与补偿

2.1 时间延迟分析

在“速度+姿态”匹配的在线标定过程中,由于延迟时间τ引起的基准信息误差分别为:

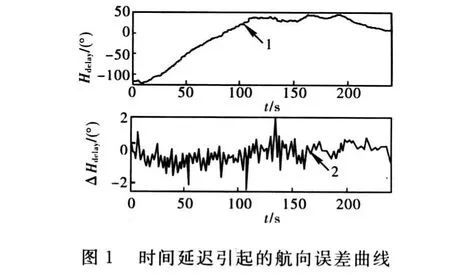
以某航次试验数据为例说明时间延迟的影响,主惯导系统的航向如图1中曲线1所示,100ms的时间延迟引起的航向延迟误差 H delay如图1中曲线2所示,可以发现100ms引起的航向延迟误差最大可达2°。主惯导系统的东向速度如图 2中曲线1所示,100ms的时间延迟引起的东向速度延迟误差 Vedelay如图2中曲线2所示,可以发现在平稳运动阶段(100～240s),V edelay相对较小,在加速运动阶段(0～100s), V edelay比较大,最大延迟速度误差可达1.5m/s。

由于时间延迟的存在,H∞滤波器接收到的基准信息的实际精度明显下降,必将降低H∞滤波估计效果,从而影响在线标定效果。因此,在进行在线标定设计时,必须对主惯导系统的时间延迟进行补偿,保证引入H∞滤波的主子惯导系统数据在滤波时间点上的同步性。

2.2 时间延迟补偿

设子惯导系统的姿态更新周期为 TSINS,H∞滤波周期为THF,主惯导系统的延迟时间为τ。在kTHF滤波时刻(k=1,2,…),由于主惯导系统延迟时间τ的存在,H∞滤波器接收到的基准信息为kT HF-τ时刻值,而子惯导系统的误差模型和观测量相关信息为kTHF时刻值。文中提出将子惯导系统同步到主惯导系统的kT HF-τ的时间同步方法,即利用kT HF时刻的观测信息Z k和k T HF-τ时刻的状态转移矩阵Φk|k-1-τ进行H∞滤波。该方法利用子惯导系统k T HF-[τ/T SINS]T SINS时刻的状态矩阵A(t)更新状态转移矩阵 Φk|k-1-τ,利用kTHF时刻的主惯导系统基准信息与kT HF-[τ/T SINS]T SINS时刻的子惯导系统相应信息的差值更新观测信息Z k,其中[·]为取整符号,即将子惯导系统的信息向前移动[τ/T SINS]个姿态更新周期,从而实现主子惯导系统的时间同步。该时间同步方法的最大同步时间误差为TSINS,TSINS一般为5～10ms,满足H∞滤波的时间同步要求。其中,状态转移矩阵和 Z k分别为 :

由此,得到对H∞滤波算法[10]加入时间延迟补偿的改进滤波递推公式如下:

1)初始化:

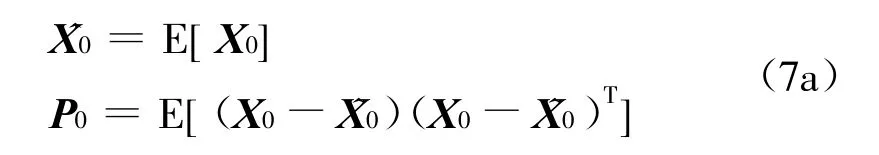
2)状态时间修正方程:

3)状态观测修正方程:

需要说明的是根据式(7)的H∞滤波递推方程估计出的系统状态 ^X k为 T OC-τ时刻的系统误差^XTOC-τ,其中 TOC为在线标定时间。因此,在进行传感器误差补偿时需要将其转换至TOC时刻的值 ^XTOC,即:

3 机载试验

由于主惯导系统的导航定位精度高,将其作为参考标准。文中设定在线标定时间为240s,以子惯导系统的600s纯惯性导航定位误差评估在线标定效果。每组试验数据分别进行以下3次试验:1)子惯导系统没有在线标定补偿直接进行纯惯性导航;2)子惯导系统首先应用文献[10]的H∞滤波方法(M1)进行在线标定,根据估计结果进行在线补偿,然后纯惯性导航;3)子惯导系统首先应用文中补偿时间延迟的H∞滤波方法(M2)进行在线标定,根据估计结果进行在线补偿,然后纯惯性导航。分别进行了7组试验,试验结果大致相同,这里选取第1组试验进行说明。

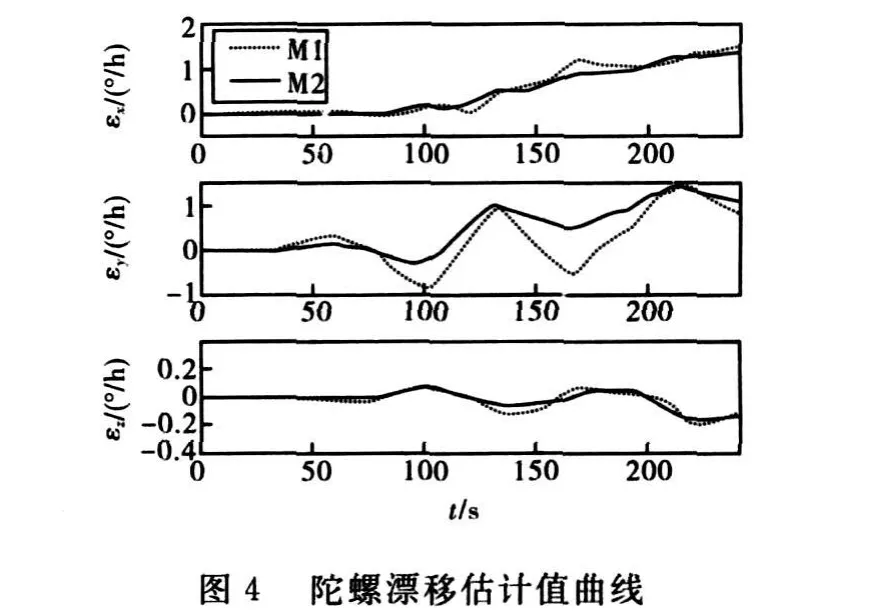
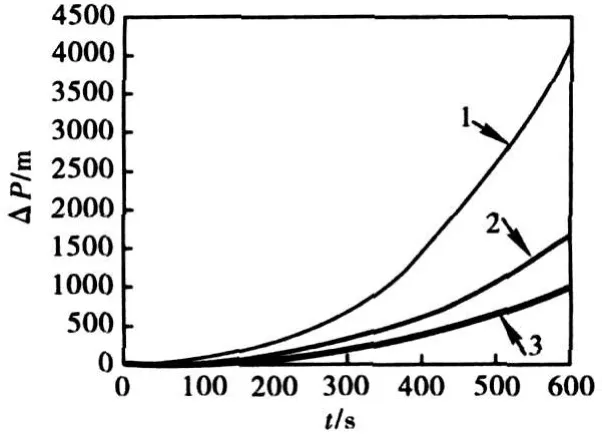
图5 定位误差曲线

M 1方法和M 2方法对失准角和陀螺常值漂移的估计值曲线分别如图3～图4所示,其中,点线为M 1方法的估计曲线,实线为 M2方法的估计曲线。可以发现由于考虑了时间延迟对滤波估计的影响,M 2方法的估计波动较小,收敛较快。图5的定位误差曲线更清楚的显示出在线标定效果,其中,曲线1为未经在线标定补偿的纯惯性导航的定位误差曲线,定位误差为4140.5m;曲线2为先应用M1方法进行在线标定、补偿后进行的纯惯性导航定位误差曲线,定位误差减小到1647.5m,导航精度显著提高,说明在线标定方法有效的标定出系统误差;曲线3为先应用M2方法进行在线标定、补偿后进行的纯惯性导航定位误差曲线,定位误差进一步减小到985.4m,说明文中提出的时间延迟补偿方法有效的提高了H∞滤波性能,进一步提高了在线标定精度。

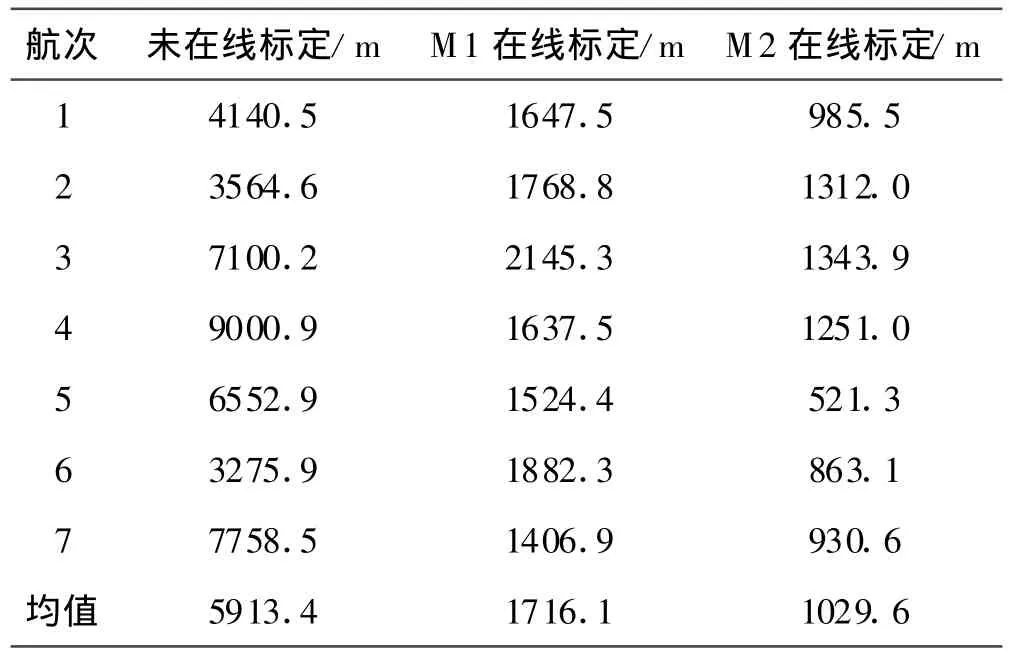
表1 定位误差列表

7组机载试验的纯惯性导航定位误差统计如表1所示,未经在线标定补偿的定位误差最大为9000.9m,平均定位误差为5913.4m;经过M 1方法在线估计补偿的最大定位误差下降到2145.3m,平均定位误差为1716.1m;通过进一步补偿时间延迟的M2方法在线标定补偿的最大定位误差进一步减小到1343.9m,平均定位误差为1029.6m,与未经在线标定相比,定位误差降低了82.6%,说明时间同步方法有效实现了主子惯导系统的时间同步,在线标定方法有效的估计出了系统误差,成功实现了弹载惯导系统的在线标定。

4 结论

文中在建立基于“速度+姿态”匹配的弹载捷联惯导系统滤波模型的基础上,设计了H∞滤波器对传感器误差进行在线标定,分析了主惯导系统时间延迟对H∞滤波估计的影响,提出并推导了一种新的具有时间延迟补偿功能的 H∞滤波方法。进行了机载试验数据的半物理仿真试验,试验结果表明经过在线标定补偿后,弹载捷联惯导系统的平均定位误差由5913.4m下降到1029.6m,导航精度显著提高,从而验证了在线标定方法的正确性和有效性。

[1] 张小跃,张春熹,宋凝芳.基于组合导航技术的光纤捷联系统在线标定[J].航空学报,2008,29(6):1656-1659.

[2] 卫育新,白俊卿.车载SINS/DR组合导航系统的在线标定方法[J].中国惯性技术学报,2009,17(6):651-653.

[3] 鲁浩,杜毅明,尉新亮.空空导弹惯导系统传递对准中飞机惯导系统参数的应用[J].航空兵器,2000(1):1-3.

[4] 徐世许,王涛.INS/GPS组合导航系统的数据精确同步方法[J].中国惯性技术学报,2008,16(5):563-565.

[5] 马云峰,周百令,万振刚,等.MIMU/GPS组合导航系统数据同步与融合方法研究[J].中国惯性技术学报,2004,12(3):28-31.

[6] 杨涛,王玮.GPS/SINS组合导航系统实现时间同步的软件方法[J].中国惯性技术学报,2008,16(4):436-438.

[7] 肖进丽,潘正风,黄声享.GPS/INS组合导航系统数据同步处理方法研究[J].武汉大学学报 信息科学版,2008,33(7):715-717.

[8] 秦永元.惯性导航[M].北京:科学出版社,2006:355-361.

[9] 陈凯,鲁浩,闫杰.传递对准姿态匹配的优化算法[J].航空学报,2008,29(4):981-987.

[10] Babak Hassibi,Ali H Sayed.Linear estimation in krein spaces,PartⅡ:Application[J].IEEE Transactions on Automatic Control,1996,41(1):34-49.