整体式头罩分离运动轨迹可靠性分析*
2011-12-07张永杰
张永杰,孙 秦
(西北工业大学航空学院,西安 710072)
0 引言
采用电视或红外成像导引头的导弹常带有跟踪视窗,为了防止视窗降低导弹的气动与隐身性能,需要整流装置改善其气动、隐身性能,当导弹到达攻击区域后抛弃整流罩[1],启动光学引导搜寻目标。在低空大气层内整流罩的分离过程主要由气动力决定[2],流动呈现高度非定常和非线性等复杂特征,并伴随着多体间强的相互干扰,具有动压大、迎风面积大、质量轻等特点,因此为保证罩体分离过程安全可靠,需要对罩体的结构重心布置、抛放的冲力、分离运动中气动力以及罩体飞行轨迹进行精细的计算和分析[3],确保分离整个过程中头罩和弹体不发生碰撞。
文中根据导弹头罩分离数值仿真结果,分析了头罩分离运动轨迹的可靠性,通过对不同飞行工况下头罩运动轨迹的可靠度计算和随机变量摄动分析,获得了一些头罩分离运动可靠性的基本规律,为头罩分离机构可靠性设计提供了基本方法和参考。
1 整体过顶式头罩分离方案
整体式分离构型具有迎风面积大、刚性好、内部可设计空间大、受突风载荷影响小等优点,多用于小型导弹的头罩分离设计,一般采用过顶式分离。罩体在分离装置[4]的推动下,从导弹的前端射出,如图1所示。该分离方式需要分离装置提供较大冲量,且冲量的反作用力主要由弹体来承受,对弹体的冲击力较大,需要设计合理的防护装置来保护弹头和内部仪器设备。

图1 整体构型过顶式分离方案示意图
1.1 基本设计参数
整体式分离罩体为锥体,罩体随体坐标系与导弹机体坐标系原点重合。文中依据设计要求,设置了三种罩体质量的重心布置方案(见表1),其中两种为偏心布置,当分离装置沿弹体轴向作用冲量力时,偏心布置的罩体将出现向上或向下偏离弹体的运动轨迹,从而增加头罩分离运动的安全性。
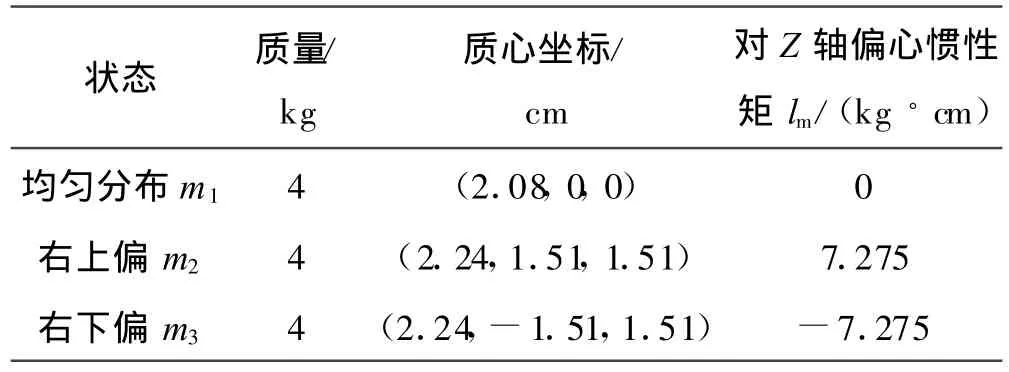
表1 质心分布与偏心惯性矩
此处头罩对Z轴的偏心惯性矩l m定义为:

式中:m为头罩质量,y c为头罩质心y坐标值;偏心惯性矩l m反映了两种偏心布置下转动惯量对罩体运动轨迹的影响。
导弹的飞行状态参数为:速度M=0.7,高度H=600m,飞行迎角分别为 α=0°,2°,4°。
受空气阻力影响,罩体脱离时分离装置必须施加冲量作用,为了获得理想的罩体分离效果设置了10k N和15k N两种冲量力,冲量力的作用时间按分离方案罩体向前运动量来控制。于是,文中将偏心布置和冲量作用组合,获得了4种罩体分离设计状态,如表2所示。
1.2 安全性定义
导弹头罩分离过程的安全性是指头罩在设计状态下脱离弹体后的运动过程中,是否有再次与弹身或弹翼碰撞的危险性,不发生碰撞则是安全的。文中研究的导弹弹翼位于弹身轴向3m处(弹体坐标原点位于弹头处),翼展长2.9m;所以罩体分离的基本安全性要求:头罩分离后,向后约3m长的运动历程中,离开弹体的距离要大于1.5m;小于1.5m,则视为不安全。
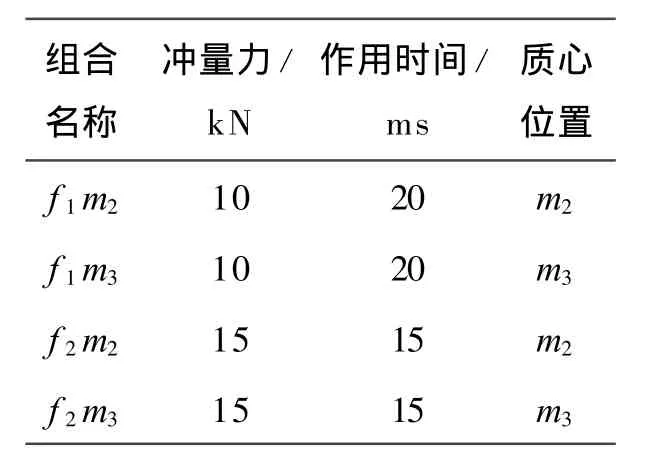
表2 分离方式作用量组合表
2 头罩分离运动轨迹可靠性分析
2.1 基本步骤
头罩分离运动轨迹可靠性分析基本步骤[5]如下:
1)通过数值计算(或试验)获得罩体分离后的运动轨迹曲线;
2)利用最小二乘方法拟合罩体运动轨迹曲线,得到拟合表达式;
3)分析拟合表达式中拟合参数与罩体质心分布、冲量、飞行迎角等因素的关系,通过多元线性回归方法建立拟合参数与飞行参数之间关系;
4)根据罩体运动轨迹拟合表达式中各随机参数的概率分布特征,建立安全边界方程,利用蒙特卡洛方法计算罩体运动轨迹的安全可靠度;
5)考察罩体运动过程中各随机参数变异系数对可靠度的影响。
2.2 不同工况下罩体运动轨迹拟合
通过不同飞行工况、不同飞行迎角条件下罩体分离数值仿真计算,可以获得罩体质心沿轴向和径向的运动轨迹曲线,如图2~图5所示。
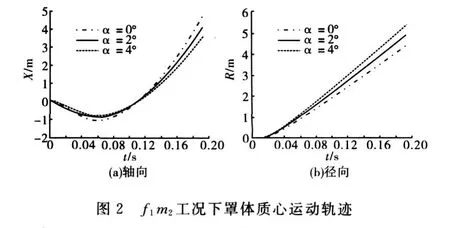
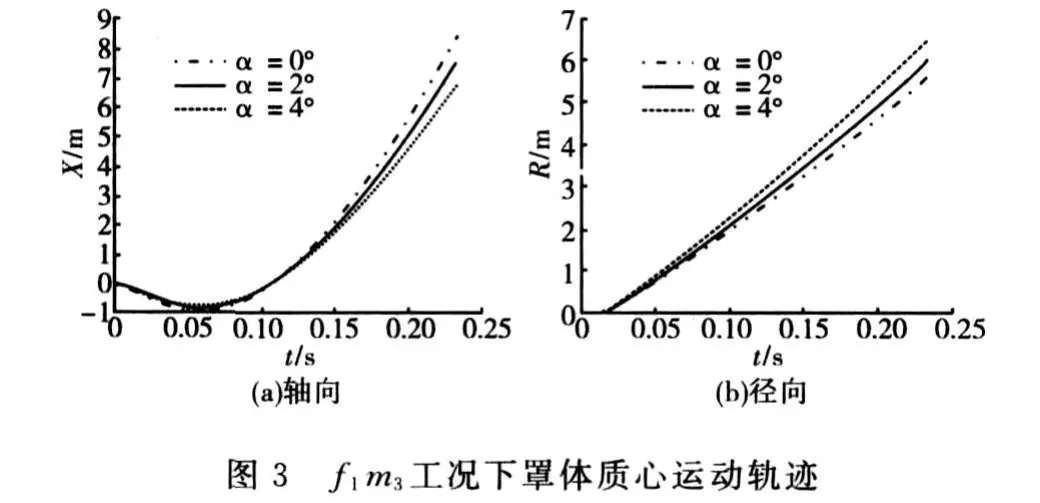
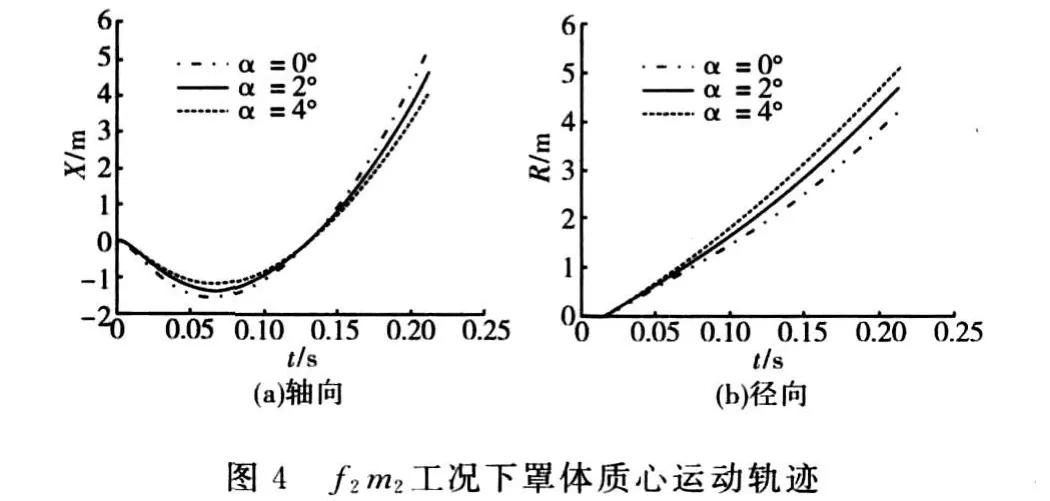
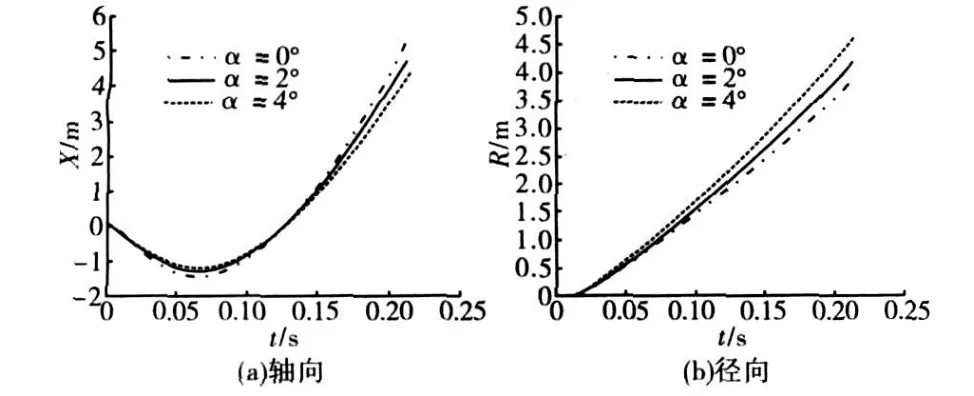
图5 f2 m3工况下罩体质心运动轨迹
利用最小二乘方法[6]拟合上述运动轨迹曲线,可以得到罩体质心沿轴向运动轨迹的多项式表达为:
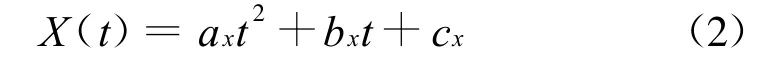
式中:ax为二次项系数,bx为一次项系数,cx为常数项。
罩体质心沿径向运动轨迹的拟合表达式为:
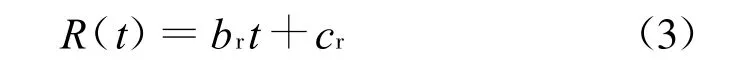
式中:b r为一次项系数,c r为常数项。
不同工况下罩体运动轨迹多项式拟合系数如表3所示。
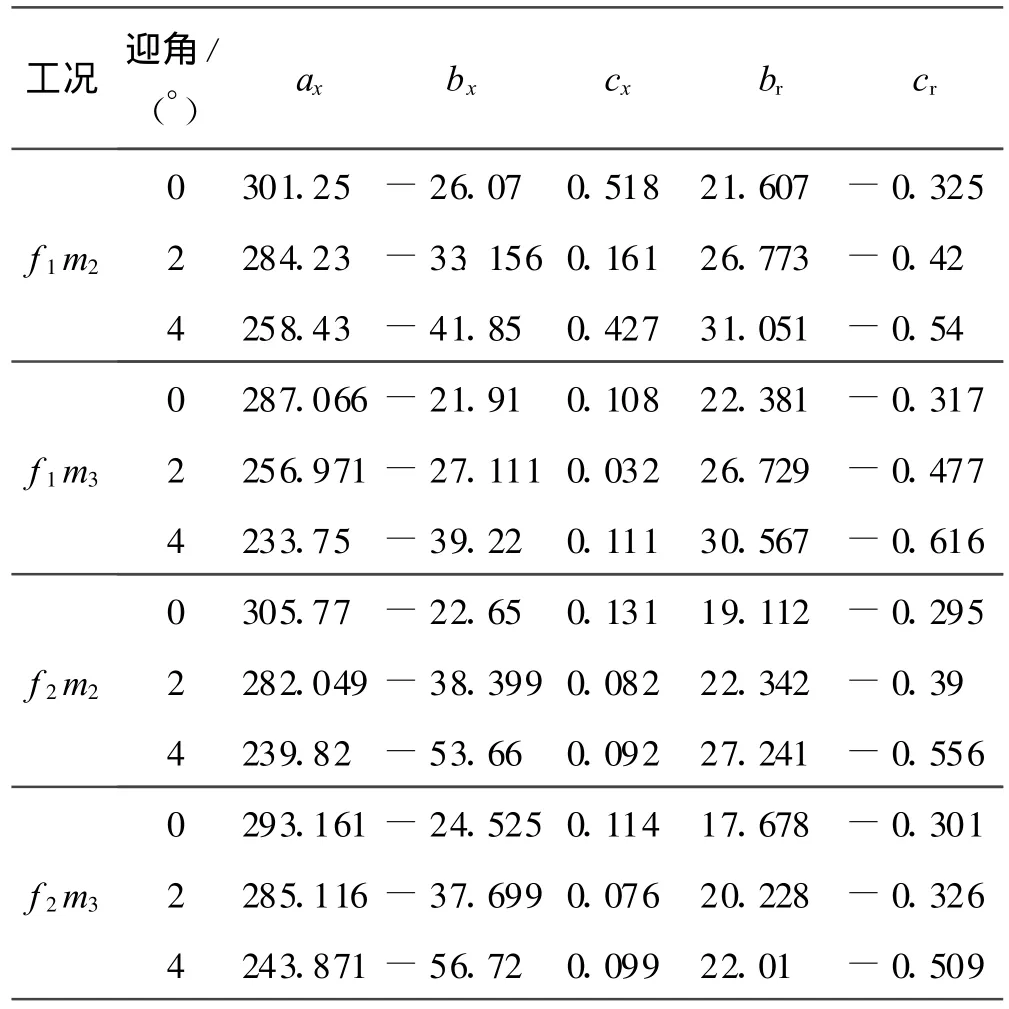
表3 不同工况下罩体运动轨迹多项式拟合系数
2.3 安全边界方程建立
定义三个随机变量:冲量f、迎角α和头罩对Z轴的偏心惯性矩l m;通过分析不同飞行工况、不同迎角下罩体质心轨迹拟合参数的取值规律,可以得出冲量、飞行迎角、偏心惯性矩与轨迹拟合参数之间存在如下关系式:

式中 :φ(f,l m,α)表示罩体运动轨迹拟合参数 ax、bx、cx、b r、c r,μi(i=1,2,…,10)为待定系数 ,ε为数值拟合误差,服从0均值正态分布。
利用表3中罩体运动轨迹拟合参数取值,通过多元线性回归方法[7],确定待定系数μi(如表4所示)。
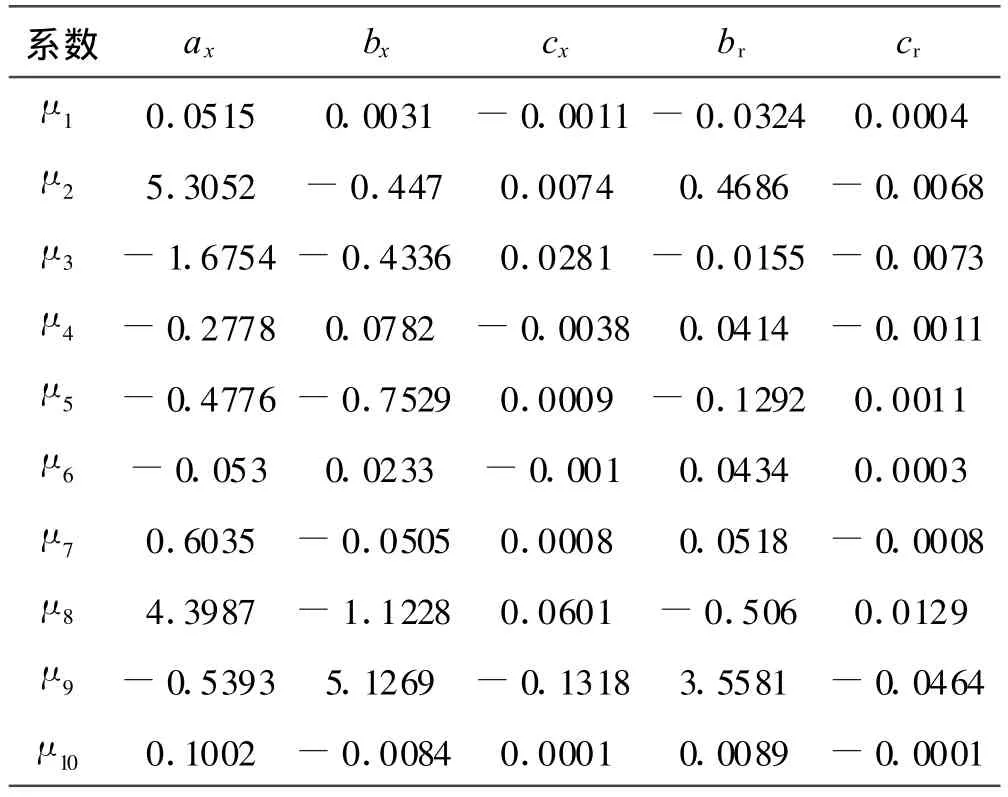
表4 多元线性回归拟合系数
根据数理统计中的大数定理[7],当数值仿真计算次数足够多时,可认为冲量力、偏心惯性矩和迎角均服从正态分布,其均值为各种飞行工况下的设计值,其变异系数[8](或方差)反映了冲量力、偏心布置、飞行姿态等因素对罩体运动轨迹的随机分散性影响,进而影响罩体运动的安全可靠性。
由罩体分离轨迹安全性定义可知,当罩体沿弹身轴向运动3m到达弹翼所在位置时,罩体沿弹身径向位移应达到或超过1.5m方才安全。于是,将罩体质心轴向轨迹拟合表达式的左端取为3,可得到此处罩体质心轴向运动时间方程:
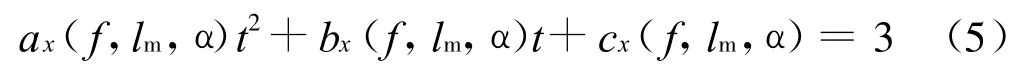
解此方程,可得到罩体沿弹身轴向运动至弹翼的时间:
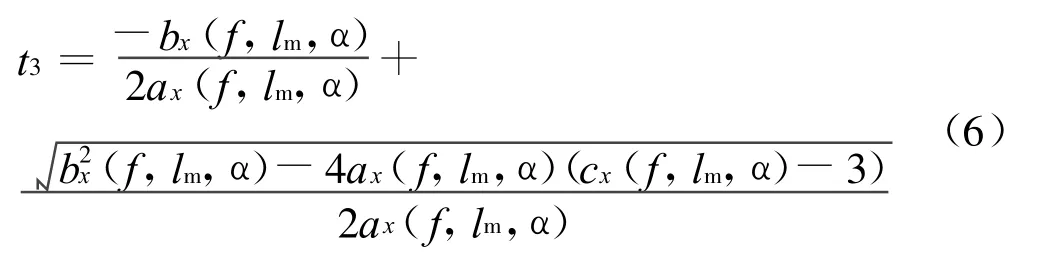
将此时间代入罩体质心径向轨迹拟合表达式,可得到此时罩体的径向位移:
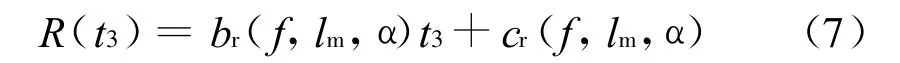
若R(t3)≥1.5,则罩体分离运动轨迹安全,罩体的飞行过程远离弹翼,不会发生碰撞;否则就是不安全的,将发生碰撞。于是,建立安全边界方程为:
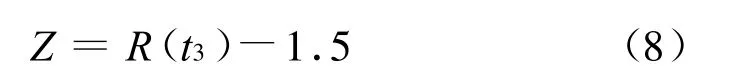
当Z≥0时,则表示罩体质心运动轨迹是安全的,P(Z≥0)就是罩体质心运动轨迹的可靠度。
2.4 可靠度计算分析
由上节中随机变量的正态概率分布特征和安全边界方程,利用蒙特卡洛方法计算各种飞行工况下罩体运动轨迹的安全可靠度如表5所示。其中冲量、偏心惯性矩、迎角的均值根据不同工况确定,变异系数取为0.15,随机误差ε的均值取为 0,方差取为 0.2。
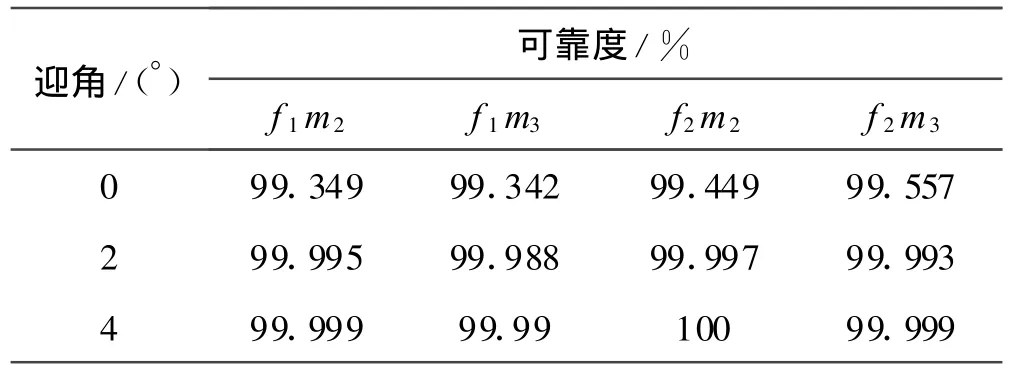
表5 不同飞行工况罩体运动轨迹可靠度
从表中可以看出:
1)罩体运动轨迹的安全可靠度较高,均在99.342%以上;
2)当冲量和偏心惯性矩保持相同水平时,随着飞行迎角的增大,罩体运动轨迹的安全可靠度增加,即:在较大迎角飞行下,头罩脱离后的飞行轨迹更加远离弹体和弹翼;
3)当冲量和迎角(正迎角)保持相同水平时,向上偏心布置的罩体运动轨迹安全可靠度高于向下偏心布置的罩体运动轨迹;即:在正迎角飞行条件下,上偏布置的罩体会获得由弹体提供的向上气动力和初速度,使罩体飞行轨迹更加远离弹体;而下偏布局的罩体没有这些优势;
4)当偏心惯性矩和迎角保持相同水平时,随着冲量的增加,罩体运动轨迹的可靠度增加;即:冲量越大,头罩脱离后的飞行轨迹离弹体越远。
2.5 典型工况随机变量摄动分析
为了分析冲量、偏心惯性矩和迎角发生摄动时对头罩分离可靠度的影响,图6给出了2°迎角下4个典型飞行工况中随机变量变异系数对可靠度的影响曲线。可以看出,偏心惯性矩发生摄动对可靠度影响相对较大,冲量发生摄动对可靠度影响相对较小。
3 总结
采用质心偏离中轴的整体式头罩设计,无论质心上偏还是下偏,罩体分离的安全可靠性都比较理想,只是在正迎角飞行时由于受到气动力和初速度的影响,向上偏心布置优于向下偏心布置;而且在大迎角飞行和大冲量推动下,罩体分离的可靠度更高。由于偏心惯性矩对罩体分离可靠度的影响较显著,因此需要精细设计偏心才能获得高可靠性的分离头罩。
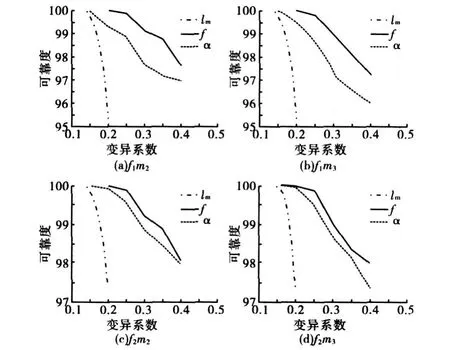
图6 随机变量变异系数对可靠度影响
[1] 周镜昆.ZN-3探空火箭头罩分离分析及弹射分离器的设计[J].宇航学报,1994,15(3):1-10.
[2] 柳森,张鲁民.再入弹抛壳气动特性研究[J].空气动力学学报,1993,11(1):16-21.
[3] Edge H L,Sahu J.Computational fluid dynamics modeling of submunition separation from missile,AAIA-99-3129[R].1999.
[4] 倪健,张铎.导弹展开机构可靠性分析和计算[J].弹箭与制导学报,2003,23(2):241-246.
[5] 王善,何建.导弹结构可靠性[M].哈尔滨:哈尔滨工程大学出版社,2002.
[6] 李庆扬.现代数值分析[M].北京:高等教育出版社,1995.
[7] 陆元鸿.数理统计方法[M].上海:华东理工大学出版社,2005.
[8] 何水清,王善.结构可靠性分析与设计[M].北京:国防工业出版社,1993.
