灰色聚类决策在武器系统研制方案优选中的应用*
2011-12-07韩晓明何婧卿
韩晓明,姜 科,张 琳,何婧卿
(空军工程大学导弹学院,陕西三原 713800)
0 引言
武器系统研制方案的评价与优选问题是武器系统研制论证过程中的重要环节,不仅决定了武器系统的性能,而且决定了70%以上的武器系统全寿命周期费用[1],因此对武器系统研制方案进行科学合理的客观评价至关重要。然而在武器系统研制方案的评价过程中,既有科研人员和系统分析人员所熟悉的白色信息,又有完全陌生的黑色信息,但更多的是科研工作者部分了解的灰色信息。因灰色系统理论善于处理贫信息,能在短资料、少信息条件下作出决策[2],因此文中尝试运用灰色系统理论中的灰色聚类决策对武器系统研制方案进行评价与优选,从而为研制方案决策提供科学的理论支持。实践证明,这种研制方案优选方法是可行的、有效的。
1 基于灰色聚类的研制方案优选模型
武器系统研制方案的灰色聚类决策,首先拟按照研制方案的要求明确若干灰类,并将研制方案各评价指标相应划分为若干灰类;其次拟通过计算研制方案的聚类系数和单位聚类系数,从而计算得到研制方案的综合决策测度;最后按综合决策测度对所有方案进行排序,即可得到各研制方案的优劣排序。
1.1 数据的归一化处理
由于武器系统研制方案评价指标大小和极性的不一致性,为了有效应用灰色聚类决策对研制方案评价优选,需要对不同意义、不同量纲且评价值在量纲上悬殊较大的指标原始数据进行归一化处理[3-4]。常见的评价值方法有多种,这里采用效用函数法[5],此方法适用范围广,对主观依赖较少,因此广为使用。具体效用函数如下:
1)趋大优型。评价指标Xj要求越大越好,则采用如下形式的效用函数:

2)趋小优型。评价指标X j要求越小越好,则采用如下形式的效用函数:

3)区间优型。评价指标X j要求在[d f,d l]范围内为适宜,则采用如下形式的效用函数:

1.2 研制方案优选的灰色聚类决策模型
1.2.1 方案评价等级及白化权函数
按照武器系统研制方案评价的要求将由优到劣划分为s类,将研制方案各评价指标的取值范围也相应地划分为s个灰类,并按照评价指标和灰类数,确定j指标k子类白化权函数(·)(j=1,2,…,m;k=1,2,…,s)。
1.2.2 指标聚类权
武器系统研制方案的各评价指标聚类权重对研制方案的优选有重要影响。聚类权重的确定可以运用德尔菲(Delphi)法与层次分析法(AHP)相结合进行实现。组织多个评判专家对研制方案的各评价指标的重要性进行两两比较,指标间的相对重要程度采用1~9标度,用比较值构造判断矩阵。设有 p个评估专家,他们的判断矩阵分别为A1,A2,…,Al(l=1,2,…,p),其中:
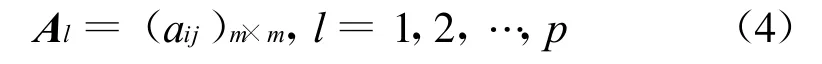
式中:aij表示第i项指标与第j项指标的比值。
将p个判断矩阵,用加权几何平均的方法获得一个综合判断矩阵 A=(aij)m×m。

式中 :λ1,λ2,…,λp 为各个专家的权重系数 。
计算最大特征根和特征向量一般采取近似方法,常用的主要有幂法、和法及根法,其中和法最为适用。和法步骤如下:
1)将判断矩阵的每一列归一化得:
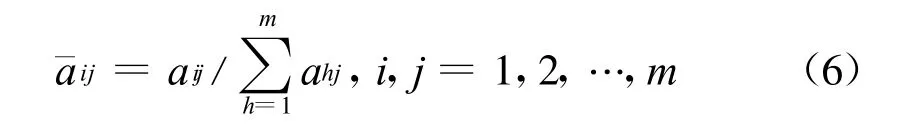
2)归一化后的矩阵按行相加得:
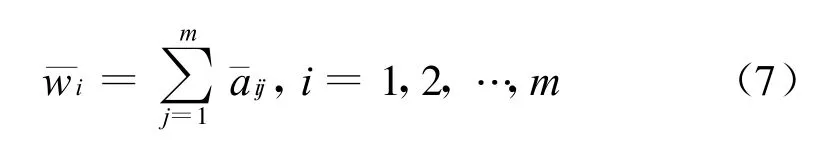

对结果进行一致性检验,从而得到的归一化特征向量可作为各评价指标的聚类权重向量。
1.2.3 方案决策系数矩阵

得聚类系数矩阵:
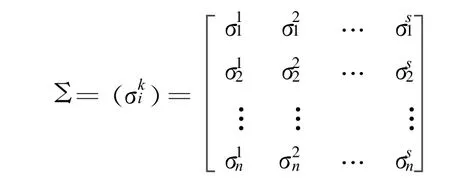
1.2.4 灰类等级

1.2.5 综合决策测度与研制方案优劣排序
为了对属于同一类灰类k的研制方案进行优劣排序,引入研制方案i属于灰类k的综合决策测度:

式中,ηk=(s-k+1,s-k+2,…,s-1,s,s-1,…,k)(k=1,2,…,s)为第k灰类的调整系数(s维)。如当s=3 时,η1=(3,2,1),η2=(2,3,2),η3=(1,2,3)。
按综合决策测度对同属于灰类k的所有方案进行排序,进而对所有方案进行优选决策。
2 应用实例
以某型地空导弹武器系统研制方案评价和优选为例,首先通过对地空导弹武器系统进行分析,建立研制方案评价指标体系;其次获取研制方案的各项指标的数据,从而建立评价矩阵;最后采用上述优选模型进行综合决策。
2.1 研制方案的评价指标与数据处理
广泛征询专家意见,深入研究了影响地空导弹武器系统研制方案的各种因素,得出系统效能、研制费用、研制周期是评价地空导弹武器系统研制方案优劣的三大要素[6]。
在地空导弹武器系统论证阶段,由专家提出了7种备选的方案,专家经过研究给出指标的具体数据如表1所示。其中,系统效能由ADC效能模型[7]进行量化得到。
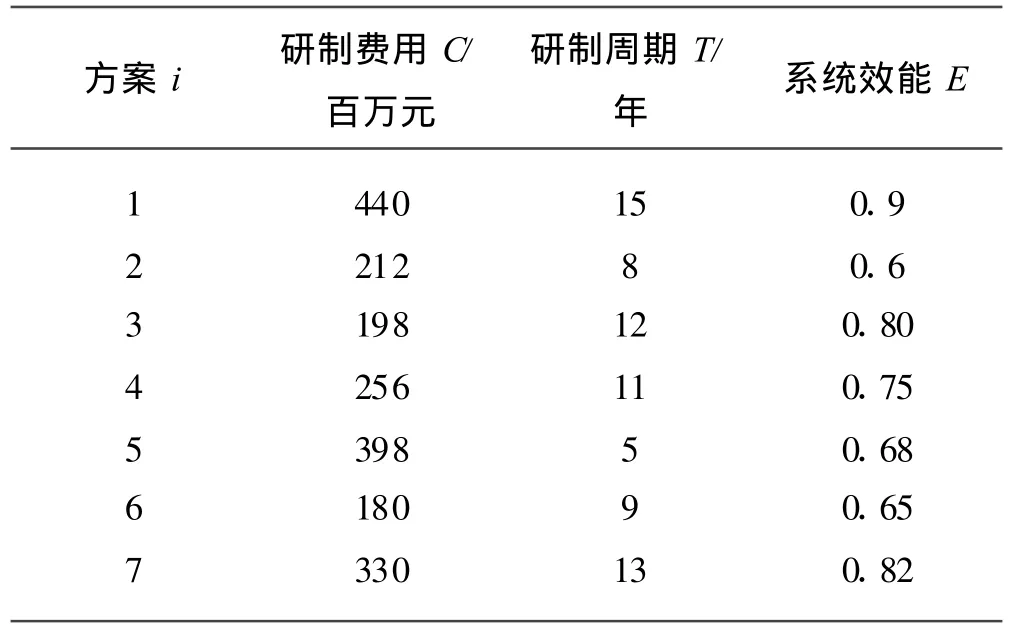
表1 某型地空导弹武器系统研制方案
在地空导弹武器系统研制方案的评价指标体系中,研制费用、研制周期指标为区间优型,系统效能指标为趋大优型。专家研究决定,研制费用处于[240,260]为好,研制周期处于[8,10]为好。对表1的数据标准化,经过处理后,消除了数据的量纲,数值处于[0,1],数值越大越好,如表2所示。
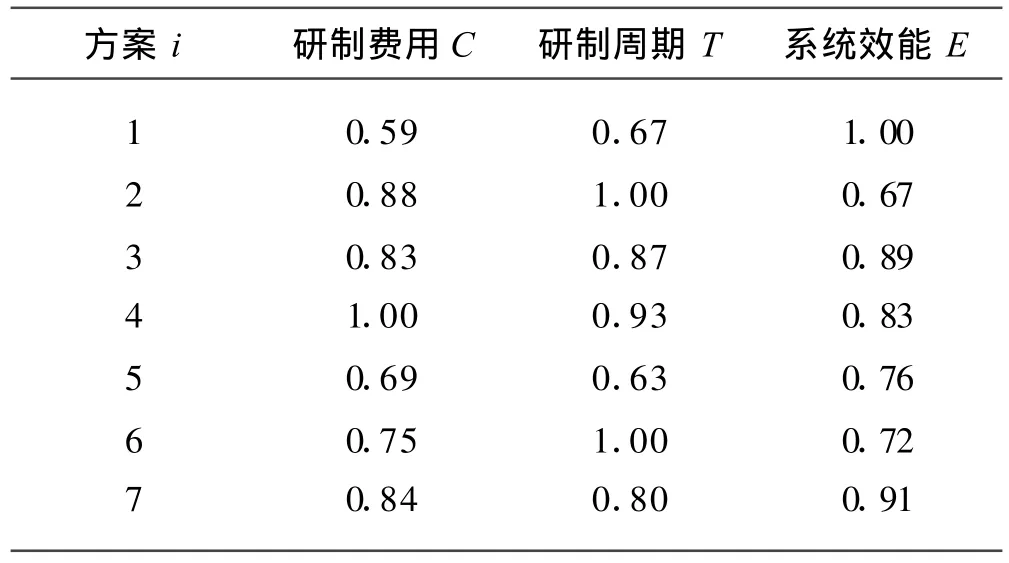
表2 某型地空导弹武器系统研制方案数据归一化处理
2.2 设定评价等级及白化权函数
按照武器系统研制方案评价的要求,将研制方案评价等级由优到劣划分为V={好,较好,差}3个评价灰类,即,k=1,2,3;s=3。
第j指标k子类白化权函数fkj(xij)(j=1,2,3;k=1,2,3)分别为:
1)对于第1灰类(研制方案好)k=1:
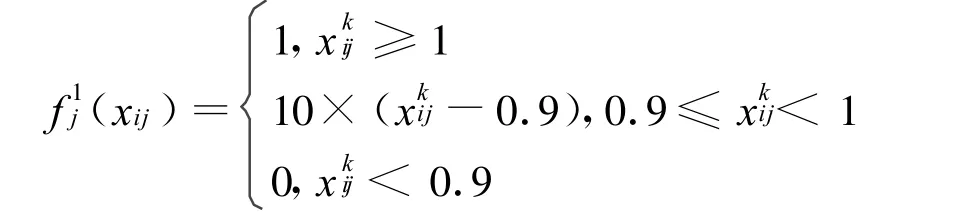
2)对于第2灰类(研制方案较好)k=2:

3)对于第3灰类(研制方案差)k=3:

2.3 确定指标权重
由5位专家根据评判准则运用德尔菲法与层次分析法相结合的方法得到地空导弹武器系统研制费用、研制周期、系统效能的权重分别为:0.4025,0.2687,0.3288。
2.4 方案灰类级别的判定
根据式 (9)求得方案i关于k灰类的灰色定权聚类系数σki,从而得到7个评价方案的聚类系数矩阵。按式(10)求取单位聚类系数得到结果如表3所示。

表3 7个研制方案的单位聚类系数
由表3可知在7个研制方案中,方案2、方案4、方案6属 “好”,方案3、方案7属 “较好”,方案1、方案5属 “差”。
2.5 研制方案的综合排序
在得到研制方案的等级后,由式 (11)计算同一等级灰类下方案的综合决策测度ωi并进行比较,可得方案的最终排序。
以评价等级为 “好”的3个方案为例,第1灰类的调整系数为η1=(3,2,1),计算综合决策测度:
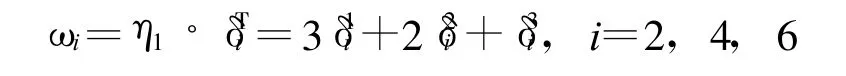
各方案的计算结果分别为:方案2为2.3798,方案4为2.6773,方案6为2.5016。
同理可得评价等级为 “较好”的2个方案的综合决策测度分别为:方案3为3.000,方案7为2.9394。评价等级为 “差”的2个方案的综合决策测度分别为:方案1为2.1900,方案5为2.5364。
通过比较综合测度可得地空导弹武器系统能够研制方案的最终排序 (由优到劣)为:
方案4≻方案6≻方案2≻方案3≻方案7≻方案5≻方案1。
对于这样的排序结果,无论从理论分析或者是与其他方法比较都是合理而可信的[8-9]。
3 结束语
基于灰色聚类决策方法探讨了武器系统研制方案优选的问题。经实例验证,利用灰色聚类决策模型进行研制方案优选,减少了人为因素的作用,所选方法思路清晰、简单易用,该方法能有效解决方案优选中 “小样本”、“贫信息”不确定性问题,适合用于武器系统研制方案的优选决策,有一定的推广运用价值。值得进一步探讨的是与其他优选方法的对比,以求取长补短,日臻完善。
[1] 吕建伟,齐欢,施文杰.基于粗糙集理论的舰船研制方案总体评价[J].数学的实践与认识,2005,35(11):127-132.
[2] 刘思峰,谢乃明.灰色系统理论及其应用 [M].北京:科学出版社,2008:74-93.
[3] 申卯兴,许进,王帅.空中目标威胁排序的灰色聚类决策方法[J].系统工程与电子技术,2008,30(9):1721-1723.
[4] 王锋,马大为,吴晓云.舰载多功能火箭武器研制技术风险的灰色聚类决策 [J].兵工学报,2008,29(3):348-351.
[5] 顾晓辉.反直升机智能雷有关总体的理论研究[D].南京:南京理工大学,2001.
[6] 李强,卜先锦.多属性群决策在武器装备研制立项中的应用[J].舰船电子工程,2008(6):10-14.
[7] 高尚,娄寿春.武器系统效能评定方法综述 [J].系统工程与电子技术,1998(7):109-114.
[8] 陈磊,董喜平,胡建辉.D-S证据推理在防空导弹武器系统研制方案优选中的应用[J].战术导弹技术,2006(3):41-43.
[9] 汪涛,方志耕,吴琳丽,等.基于通用特性的武器系统研制方案优选方法[J].军械工程学院学报,2008,20(3):15-18.
