修正Jaulent-Miodek方程组的G′/G展开和精确解

陈南

(厦门工学院 计算机与人工智能学院，福建 厦门，361021)

非线性偏微分方程的求解问题一直受到广大学者的关注。目前，已有很多方法对方程求解，例如齐次平衡法[1]、达布变换法[2]、Painlevé分析法[3]、G′/G函数展开法等。G′/G展开法是由 WANG等[4]提出的，人们对G′/G展开法[5-6]进行了深入研究，并对该方法进行了多种推广。本文研究的修正Jaulent-Miodek方程组

(1)

来源于文献[7]，是从1个2×2谱问题中递推出来的孤子方程族中第1个方程。文献[8]利用Painlevé分析的方法、文献[9]利用Tanh函数法和扩展Tanh函数法、文献[10]用改进的双曲函数法对方程组(1)进行研究。用G′/G展开法对修正Jaulent-Miodek方程组进行求解，获得了方程组的双曲函数、三角函数、有理函数6组不同形式的精确解。

1 应用G′/G展开法

首先，对方程组(1)进行行波变换：

u(x,t)=u(ξ),v(x,t)=v(ξ)，ξ=x-ct

(2)

式中：c为待定常数，方程组(1)化为

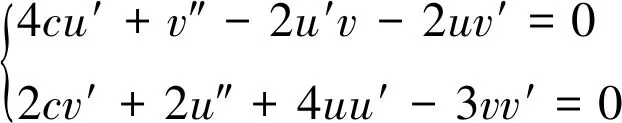
(3)

假设方程组(3)具有G′/G多项式形式的解，即

(4)

G=G(ξ)满足如下方程：

G″+λG′+μG=0

(5)

式(4)中：a0,a1,a2，…，am和b0,b1,b2，…，bn以及式(5)中的λ和μ均为待定常数，且am≠0，bn≠0。将(4)式代入方程组(3)中，这时，方程组(3)左边变成一个关于G′/G的多项式，通过平衡线性最高阶导数项与最高阶非线性项的幂次，可得

n+2=m+n+1

m+2=max(2m+1,2n+1)

(6)

求解(6)，可得m=1,n=1。于是，可设方程组(1)的解为

(7)

则

(8)

(9)

(10)

(11)

将式(8)，(9)，(10)和(11)代入方程组(3)中第1个方程，可得

(12)

b1+2a1b1=0

(13)

-4ca1+3b1λ+2a1b0+2a0b1+4a1b1λ=0

(14)

-4ca1λ+b1λ2+2b1μ+2a1λb0+4a1b1μ+2a0b1λ=0

(15)

-4ca1μ+b1λμ+2a1b0μ+2a0b1μ=0

(16)

将式(8)，(9)，(10)和式(11)代入方程组(3)中第2个方程，可得

(17)

(18)

(19)

(20)

-2cb1μ+2a1λμ-4a0a1μ+3b1b0μ=0

(21)

计算式(13)～(16)，(18)～(21)得

(22)

2 修正Jaulent-Miodek方程组的精确解

对代数方程组(22)进行计算，求得2组解：

(23)

(24)

对于第1组解，将式(23)代入式(7)，得方程组的解为

(25)

情况1：当λ2-4μ>0时，

(26)

式中：C1和C2为任意常数。将式(26)代入式(25)，得到方程组的双曲函数解为

情况2：当λ2-4μ<0时，

(27)

将式(27)代入式(25)，得到方程组的三角函数解为

情况3：当λ2-4μ=0时，

(28)

将式(28)代入式(25)，得到方程组的有理解为

对于第2组解，将式(24)代入式(7)得方程组的解为

(29)

情况1：当λ2-4μ>0时，

(30)

式中：C1和C2为任意常数。将式(30)代入式(29)，得方程组双曲函数解为

情况2：当λ2-4μ<0时，

(31)

将式(31)代入式(29)，得方程组三角函数解为

情况3：当λ2-4μ=0时，

(32)

将式(32)代入式(29)，得方程组有理解为

3 结论

求解非线性偏微分方程，一直是一个重要的问题。本文利用G′/G展开法对修正Jaulent-Miodek方程进行求解，得到了三角函数、双曲函数和有理解6组不同形式的精确解。后续，可以用G′/G展开法的推广形式来求解修正Jaulent-Miodek方程，进一步丰富该方程组的解系。