2011年高考数学三角函数试题特点分析

●

(嘉兴市第一中学 浙江嘉兴 314050)

2011年高考数学三角函数试题特点分析

●沈新权郑俊炜

(嘉兴市第一中学 浙江嘉兴 314050)

三角函数是描述周期现象的数学模型，在数学和其他学科领域中具有非常广泛的应用，因此它是高中数学乃至高等数学的重要基础知识之一．高中新课程标准中的三角函数内容主要包括三角函数的定义、诱导公式、同角三角函数的基本关系、三角函数的图像和性质、两角和与差的三角函数、简单的三角恒等变换以及解三角形等．新课程高考重视对三角函数的图像和性质的考查，重视对三角函数基础知识和基本技能的考查．

1 命题特点和知识类型

纵观2011年全国各省市的数学高考试卷，我们发现2011年对三角函数部分的考查保持了内容、题量、分值的稳定，难度适中．其考查方向主要涉及3个方面：一是三角函数的图像和性质；二是简单的恒等变换；三是解三角形问题．解题过程一般是先进行恒等变换，再利用三角函数图像和性质解题．对能力的考查主要是演绎推理能力、计算能力、综合应用知识解决问题的能力，体现的数学思想有化归转化思想、分类讨论思想、函数思想等．

1.1 三角函数的图像和性质

三角函数的图像与性质是高考重点考查的内容之一，从2011年各省市的高考数学试卷来看，选择题、填空题、解答题都有对三角函数的图像和性质的考查，试题难度中等或中等偏易．

(1)三角函数的概念及同角三角函数的基本关系.

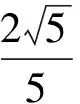
(2011年江西省数学高考文科试题)

分析本题重点考查三角函数的定义．由正弦函数的定义得

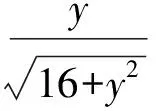
从而y<0，解得y=-8．

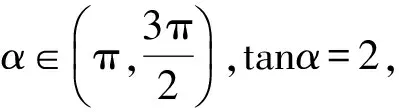
(2011年全国数学高考大纲卷文科试题)

分析本题考查同角三角函数的基本关系．由

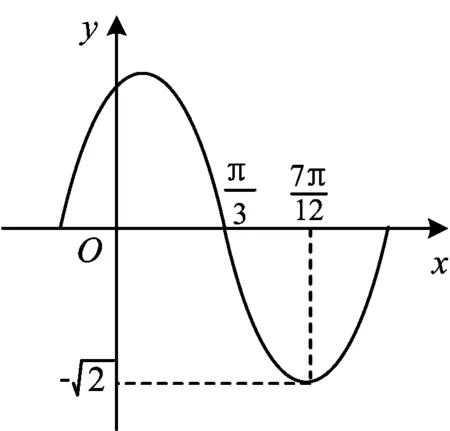
图1

且

解得

(2)三角函数的图像.

例3函数f(x)=Asin(ωx+φ)(A,ω,φ是常数，A>0,ω>0)的部分图像如图1所示，则f(0)=________．

(2011年江苏省数学高考试题)

分析本题主要考查由y=Asin(ωx+φ)的图像写出其解析式，以及诱导公式和数形结合思想．

由图像可知

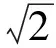
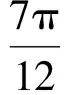
得

因此

类似的问题还有2011年辽宁省数学高考试题理科第16题、文科第12题．

(3)三角函数的性质.

( )

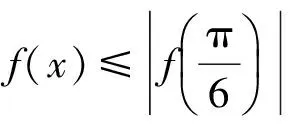
(2011年安徽省数学高考理科试题)

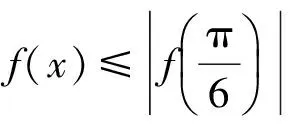
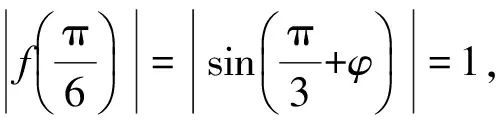
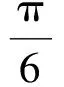
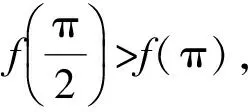
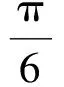
从而

( )

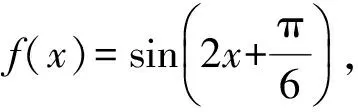
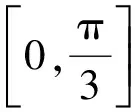
(2011年山东省数学高考理科试题)

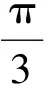
1.2 简单的三角恒等变换

三角恒等变换是解决三角函数问题的重要工具，2011年的数学高考试卷中主要考查利用三角恒等变换来求值、证明或者求解三角函数的性质问题．

( )

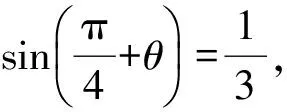
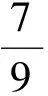
(2011年辽宁省数学高考理科试题)

分析本题是简单的三角函数求值问题，可以通过两角和的正弦公式得到sinθ+cosθ的值，再平方求出sin2θ的值；也可以利用诱导公式，再结合二倍角的余弦公式求出sin2θ的值，即

这样的三角函数恒等变化问题在2011年各省市的数学高考试卷中屡见不鲜，如2011年江苏省数学高考试题第7题也有类似的做法．

例7已知函数

(1)求f(x)的最小正周期和最小值；

(2011年四川省数学高考理科试题)

1.3 解三角形

2011年的数学高考重视对解三角形知识的考查，其考查特点是综合三角函数知识考查正弦、余弦定理在解三角形、三角恒等变换以及实际问题中的应用．

(2011年全国新课标数学高考理科试题)

分析本题主要考查了解三角形与三角函数问题.需要从正弦定理、三角恒等变换、三角函数的性质这3个方面入手．由正弦定理得

AB+2BC=2sinC+4sin(120°-C)=

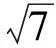
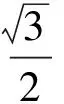
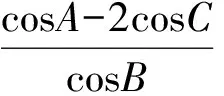
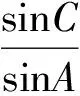
(2011年山东省数学高考理科试题)

2 亮点扫描

2.1 新颖问题随处可见

(1)求f(x)的最小正周期及φ的值；

(2011年浙江省数学高考文科试题)

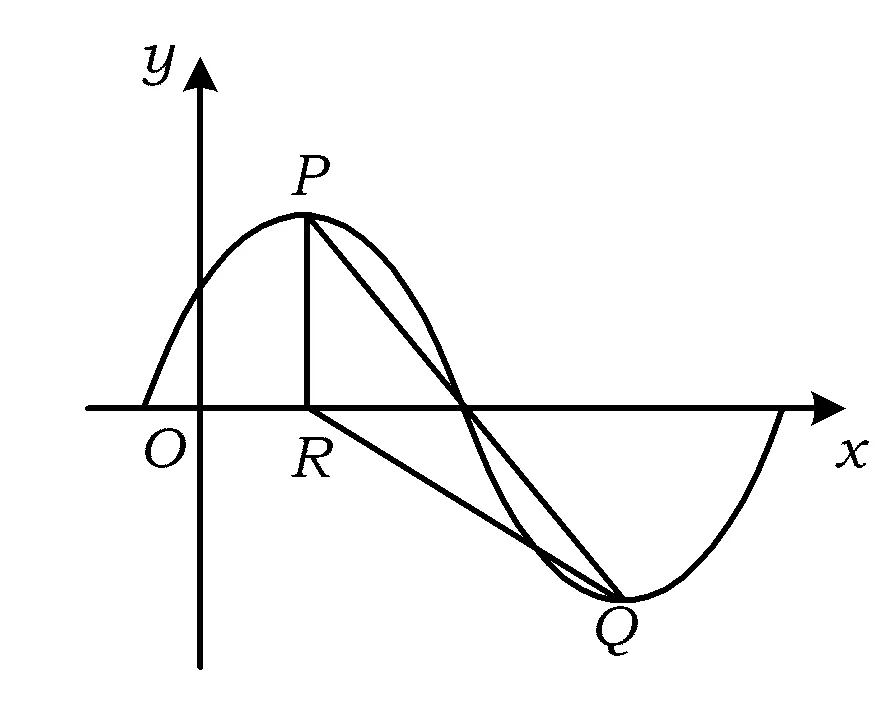
图2

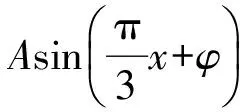
2.2 数学思想之花处处开放

( )

A．没有零点

B.有且仅有1个零点

C.有且仅有2个零点

D.有无穷多个零点

(2011年陕西省数学高考理科试题)

分析本题可以根据函数的性质(值域、单调性等)进行判断，但其解法较烦.如果利用数形结合的思想方法进行判断，则结论直观、清晰．以三角函数的知识为载体考查学生的数形结合思想、化归转化思想、函数方程思想等是2011年数学高考的又一亮点．

2.3 知识交汇时隐时现

(2)若点P(x，y)为平面区域{x+y≥1,x≤1,y≤1}上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．

(2011年福建省数学高考文科试题)

分析本题在三角函数与线性规划的知识交汇处命题，给人以耳目一新的感觉.问题的求解并不复杂，但对考生知识的全面性和完整性则有较高的要求．

3 复习建议

由于高考中对三角函数内容的考查难度以中等或中等偏易为主，但对大部分数学基础不太理想的学生来讲，三角函数公式多，解题头绪杂，因此在复习中为了提高学生三角函数的解题能力，可以采取“智取为主，强攻为辅”的复习教学策略.

3.1 重视三角函数公式的复习，展示三角函数公式的内在联系

三角函数中的公式是进行三角计算的基础，也是三角变换的基本工具．2011年陕西省数学高考的文、理科试题都考查了余弦定理的证明，由此可见命题教师的良苦用心．三角公式虽然多，但它们之间都有一定的内在关系，譬如诱导公式的主要功能是把任意角的三角函数转化为锐角三角函数，具有“奇变偶不变，符号看象限”的内在联系；又如在两角和与差的三角函数中，两角和或差的余弦公式是所有这些公式的“母公式”，两角和与差的其他公式、倍角公式等都可以由它们推导出来．因此，在复习过程中我们要教会学生理清公式之间的关系，在理解的基础上熟悉、记忆公式，注重公式的变形和逆用，把公式归类、条理化、系统化．

3.2 关注三角函数解题规律的总结，突破三角函数问题解决的瓶颈

在现行的课程标准中，三角函数问题虽然难度不高，但由于三角公式多、问题变化多的特点，不少基础差的学生把三角函数视为“拦路虎”.为了解决这一问题，在复习过程中除了重视对三角函数公式的复习以外，还应该要关注学生对三角函数解题过程的规律总结．例如对于化简与求值题，常用的方法有：角的配凑、平方降次、切化弦、诱导公式、同角三角函数的基本关系引路、利用辅助角公式等转化为同名三角函数的函数，其主要目的是将未知角变换为已知角进行求解；与三角函数的性质有关的问题，要有目标意识，合理运用基本公式，把三角函数式转化为一个角的一种三角函数的形式，其间常用的方法有：图像变换、整体代换等；对于解三角形问题，借助正、余弦定理进行边、角互化，结合题目条件把边转化为角或把角转化为边．

3.3 强化数学思想方法的教学，培养学生整体的数学思维

在三角函数的教学和复习中，要引导学生用函数的观点来理解三角函数，强调角度与函数值的对应关系，引导学生时刻抓住角度、象限、符号三者之间的关系，时刻把三角函数中的内容同函数中的相关内容作对比.同时要让学生了解，三角函数作为函数，它的一个基本性质就是周期性，这是三角函数不同于其他函数的最基本的东西．另外，整个三角函数都是在直角坐标系下学习的，这也充分体现了解析几何思想，而解析几何的最基本特征就是数形结合．因此，数形结合给三角函数增添了形象性、直观性，也能够提高学生学习三角函数的兴趣和积极性．除此之外，数学中常见的数学思想如转化与化归(角与角的转化、角与边的转化、函数名称之间的转化等)、函数与方程的思想、换元的思想、整体的思想等在三角函数的教学内容中都有淋漓尽致地体现．在复习中，借助三角函数这一教学内容，强化数学思想方法的教学，才能使得学生在整体上把握住三角函数，使得学生在更高的高度上理解、掌握三角函数，从而提高教学，提高复习实效．