教学创新课例：数列复习课

●

(太和中学 安徽阜阳 236600)

教学创新课例：数列复习课

●周欣

(太和中学 安徽阜阳 236600)

在数学教学改革的浪潮中，各种体现新理念的教学模式层出不穷.如何在这种形势下使课堂教学出新又出彩，既让学生主动探求、获取的知识，发展思维，增长能力，又在充满悬念和矛盾冲突的教学活动中，让学生领略数学的魅力，使教与学成为师生的一种共同享受，这是广大数学教师所努力追求的一种高境界.笔者在公开课“数列习题课”的教学中完全打破传统的模式，进行大胆尝试，取得了预期的效果，受到了学生和听课教师的好评.笔者将这节课教学过程中富有特色的部分介绍如下，并进行了必要的评析.

1 教学过程节录

例1在等差数列{an}中，a10=100，a100=10，求a110.

学生发现题目虽简单，但极有特点，跃跃欲试.

分析求a110可先求出什么，如何求？一般是求首项和公差，可由a10=100，a100=10列出方程组解出首项a1及公差d.

解法1由已知得

解得

a1=109，d=-1,

于是

a110=109+109×(-1)=0.

学生较快得出解法2.

解法2由a110=a10+90d,得

d=-1,

于是

a110=a100+10d=10-10=0.

解法2实际上是将等差数列通项公式进行推广，通常an=a1+(n-1)d.根据等差数列的定义可得

an=a2+(n-2)d;

an=a3+(n-3)d;

…

an=an-1+d.

一般结论为an=am+(n-m)d.

上面推广的结论可以解决什么问题？若是等比数列，则有无类似结论？

学生小结已知任意2项可以求出首项和公差，对应等比数列有：an=a1qn-1，an=a2qn-2…，an=amqn-m.

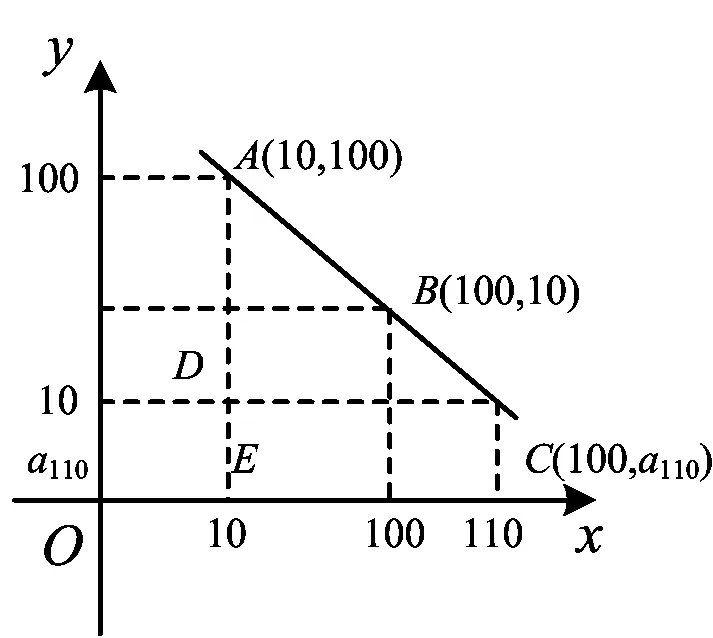
图1

当学生没有新解法时,教师启发：数列实际上是一种特殊函数.从这一角度上看，我们可以怎样理解数列？

画图展示，数列就是按照一定顺序排成的一列数.

从函数的观点看，数列是定义在N*或其有限子集{1,2,3，…，n}上的函数f(n).当自变量从1开始依次取正整数时，f(n)所对应的一列数值：f(1),f(2),f(3),…,f(n).

引导学生得到：(1，a1)，(2，a2)，…,(n,f(n)),就是一次函数f(n)=an=nd+(a1-d)图像上散开的点.进一步启发学生,本题实际上涉及到3个点：A(10,100)，B(100,10)，C(100，a110).

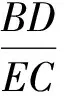
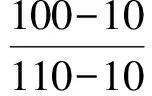
解得

a110=0.

反思在学习本章内容时,要善于从函数的角度去理解数列，继续引导学生仔细观察：此题的条件与结果有何特点？它们之间是否是巧合呢？

师生共同探究、观察、讨论得出(由学生总结):

(1)条件的2项与项数刚好交换；

(2)要求项的项数恰好为已知2项的项数和；

(3)大胆猜想：{an}为等差数列，若am=n，an=m，则am+n=0.

由等差数列的性质an=am+(n-m)d得出d=-1,于是am+n=an+md=m-m=0.

变式若将原题中的a10，a100，a110分别改为S10,S100,S110，即和的形式，会有什么好的解法、好的发现？

学生思考，教师巡视，等大多数学生做完后，组织学生发言，教师作点评.

解法1设数列{an}公差为d，首项为a1.由

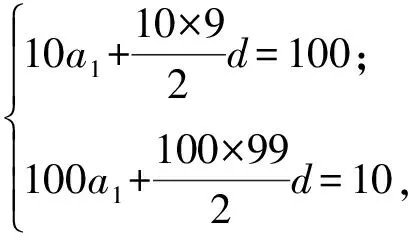
解得

从而

教师点评这是根据等差数列前n项和公式进行思考，利用了方程的思想，思路严谨，但计算量大，运算过程极易出错.

解法2由已知得

式(1)-式(2)得

从而

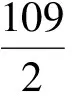
学生可能会仿照前例解法3，用函数的观点解题，但可能思维受阻.

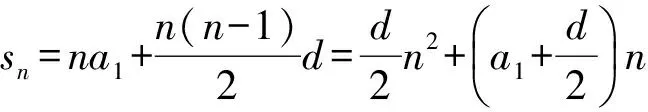
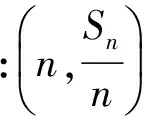
由an与Sn的关系an=Sn-Sn-1(n≥2),揭示了an与Sn之间的关系.以上变式就是用Sn来代替an得到的一道题，那么是否可以大胆地猜想用等差数列的和作为项构成一个新的数列是等差数列呢？

不妨试一试，首先，S1,S2,S3,…,Sn能否构成一个新的等差数列？为了说明此问题，可以举例.如1,2，3，…，n，则S1=1，S2=3，S3=6，….

教师启发从an=sn-sn-1(n≥2)本身去想，即a1=s1,a2=s2-s1,a3=s3-s2,a4=s4-s3,…，得来全不费功夫！s1，s2-s1，s3-s2,s4-s3,…，sn-sn-1就是a1,a2,a3,…,an这个数列本身！由此学生思维活跃起来，联想到前面习题、练习中的类似问题，此时合理引导，做到活而不乱.

引导学生归纳和推广：(1)若{an}为等差数列，则Sk,S2k-Sk,S3k-S2k，…也是等差数列，公差为kd；(2)若{an}为等比数列，则Sk,S2k-Sk,S3k-S2k，…也是等比数列，公比为qk.由以上分析，得解法4.

解法4由S10,S20-S10,S30-S20,…,S110-S100成等差数列,设公差为d′，则

S100=S10+(S20-S10)+…+(S100-S90)=

由S10=100,得d′=-22，于是

S110=S10+(S20-S10)+…+(S110-S100)=

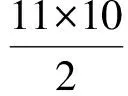
解法4实际上构造了一个新的等差数列，思路显得更广.

得

a11+a100=-2.

-110.

学生总结a11+a100=a1+a110，推广至如p+q=m+n，则ap+aq=am+an；类比到等比数列可得ap·aq=am·an.

从以上解法可看出：对概念认识得越清，产生的解法越简捷，而最后一种解法揭示了问题的内在涵义.

2 对上述教学特色的简评

2.1 倡导积极主动、勇于探索的学习方式

传统的复习课一般是整理教科书中的内容，梳理知识网络，巩固基础，回顾基本方法，训练基本技能.基本上是教师讲、学生听，学生主动性较差.而学生的数学学习活动不应只限于接受、记忆、模仿和练习，高中数学课程还应倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式.这些方式有助于发挥学生学习的主动性，使学生的学习过程成为在教师引导下的“再创造”过程.而本节课正是以一道不起眼的“小题”为引子，深入挖掘，通过“一题多解”、“一题多变”等灵活多样的形式进行研究性复习，不仅有效地复习了数列这一章的基本知识，而且为学生创造许多创新的机会，学生思维得以优化.

2.2 注重体现数学思想，着眼培养创新能力

本节的研究性复习是根据课本的脉络，将复习内容转换为研究专题，主动获取知识，应用知识解决问题的学习活动，具有主动性、深刻性、开放性等特点，并把知识上升到数学思想.如例1中的解法1和解法2应用方程思想，解法3应用数形结合思想、函数思想；例2揭示an与Sn的关系理解数列和的本质，例2中解法4应用了尝试、猜想、类比等方法，解法5是从思维深刻性转到思维批判性.整个设计通过一道不起眼的“小题”创设情境，从具体实例出发，展现数学知识的发生、发展过程，使学生能够从中发现问题、提出问题，鼓励学生在经历数学的发现和创造过程中，养成独立思考、积极探索的习惯，发展学生的思维，培养学生的创新能力.

2.3 返璞归真，强调本质

数学课程要讲逻辑推理，更要讲道理.通过例1这一典型例子的分析和学生自主探索活动，使学生理解数学概念、结论逐步形成的过程，体会蕴涵在其中的思想方法，追寻数学发展的历史足迹，把数学的学术形态转化为学生易于接受的教育形态.通过对这道不起眼的“小题”进行“一题多解”、“一题多变”及类比、猜想、论证等，力求通过各种不同形式的自主学习、探究活动，为学生形成积极主动的、多样的学习方式创造有利的条件，以激发学生的数学学习兴趣，又不失时机地揭示数学知识的本质，如例2中的解法5.

[1] 涂荣豹.谈提高对数学教学的认识[J].中学数学教学参考(高中)，2006(1-2)：13-15.

[2] 罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2001.

[3] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：北京人民教育出版社，2003.