巧用“三招”，求数列不等式中项数n的最值

庞羽

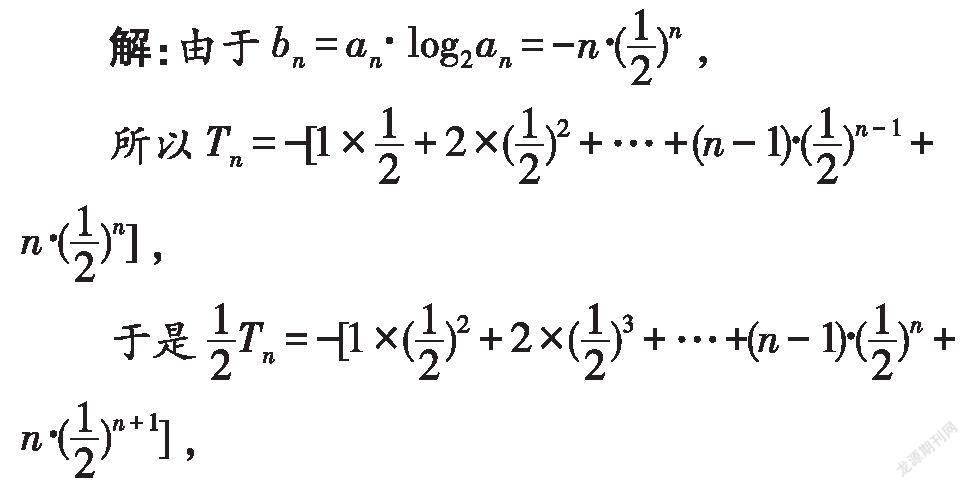
数列不等式问题具有较强的综合性.解答此类问题，不仅要灵活运用数列与不等式知识，还需将问题与其他知识关联起来，才能顺利解题.虽然数列不等式与常规不等式较为相似，但是其未知数是正整数，且各项呈现一定的规律，因此我们可以采用一些“妙招”来求解.在求数列不等式中项数n的最值时，可根据数列的特点和不等式的结构特征，灵活变通，寻找解题的思路.

一、将不等式转化为常规不等式

在求数列不等式中项数n的最值时，可先对给出的数列表达式进行变形、化简，将其转化为一个关于自然数n的常规不等式，再通过解不等式确定n的取值范围，求得项数n的最值.

解析：首先可求出数列{b}的前n项和为T，再根据题意，采用错位相减法求和，以便将不等式转化为关于自然数n的常规不等式，通过解不等式求得n的最值.

将两式相减得：

二、利用数列的单调性

数列是一种特殊的函数.在求数列不等式中项数n的最值时，可将求数列不等式的一部分看作是关于自然数n的函数，根据基本函数的性质判断出数列的单调性，然后运用数列的单调性确定数列项数n的最值.

所以n的最大值为4.

在解答数列不等式的过程中，可根据解题的需要，构造出函数模型，然后判断此数列的单调性，再根据数列的单调性寻找到符合题意的n的最值.这个解题方法是非常有效的.

三、放缩不等式

有些数列不等式非常复杂，我们很难采用常规方法求得最值，此时可根据数列不等式的特点，将不等式进行合理的放缩，构造出新的数列，将数列转化为等差、等比数列，或易于求和的数列，以便将数列不等式简化，求得n的最值.

由于S+2T≥2021，

所以最小正整数n的值为45.

本题中的不等式比较复杂，寻找数列各项的规律以及求出数列的和是解题的关键.可通过放缩不等式，求得数列的和，使问题得解.

求数列不等式中项数n的最值的实质是解含有数列的不等式，因此在解题时，需先明确数列的特点、规律，然后化简、变形不等式，再求最值.同学们可根据不等式的特點，采取的不同方法，如将不等式转化为常规不等式、挖掘数列的单调性，或通过放缩不等式进行求解.