目标规划的图解法与等值线

宋晓新, 肖运海

(河南大学数学与信息科学学院,河南开封 475001)

目标规划的图解法与等值线

宋晓新, 肖运海

(河南大学数学与信息科学学院,河南开封 475001)

运用和发展了等值线的思想方法,研究目标规划中的多目标决策问题的图解法,提出了运用改进等值线方法研究多目标决策问题的新思路.

改进等值线方法;目标规划;多目标决策问题

1 引 言

我校当前正在使用的《运筹学》(第三版)教材的编著者是国内最优秀的各个领域的专家,此教材经过了多次的修改和完善,是一部内容深入浅出,文字通俗易懂的高水平教材.但是在多目标规划的图解法这个小问题上,仍然有需要改善的地方.本文作者希望能够对此教材的进一步完善贡献自己的一份绵薄之力.本文中将用改进等值线方法来解决这一问题.

目标规划方法是解决多目标决策问题的方法之一.一个规划问题常常有若干目标.但是决策者在要求达到这些目标时,有主次或轻重缓急的不同.对于各个目标我们赋予不同的优先因子.若要区别具有相同优先因子的两个目标的差别,这时可分别赋予它们不同的权系数wj,这些都由决策者按具体情况而定.

2 课本上的例子

下文中我们将给出《运筹学》(第三版)第103页例3的数学模型以及课本上的图解法证明.原题与本文关系不大,故略去.

解 设x1和x2分别表示彩色和黑白电视机的产量.这个问题的目标规划模型为

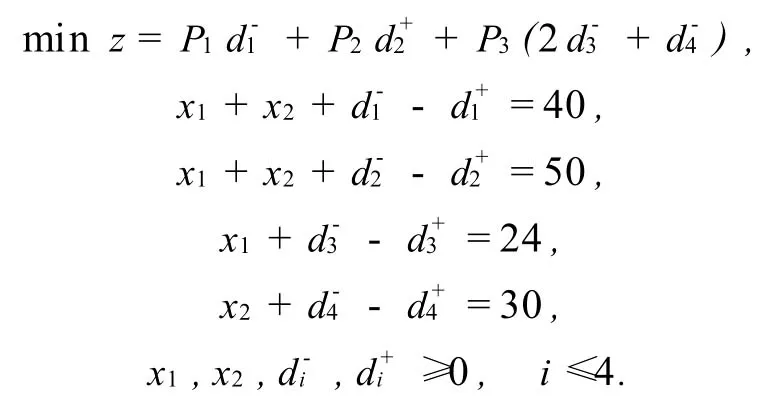
图1

用图解法求解,见图1.从图中看到,在考虑具有P1,P2的目标实现后,x1,x2的取值范围为AB CD.考虑P3的要求时,因为d-3的权系数大于d-4,故先考虑mind-3,这时x1,x2的取值范围缩小为AB EF区域.然后考虑mind-4,最终取E(24,26)为满意解.由于d-3与d-4是具有相同优先因子的两个目标函数,因而在上述证明中采用的先考虑mind-3,后考虑mind-4的研究路线是值得探讨的.

3 改进等值线方法

在第一章中,我们定义具有相同目标函数值的点的集合构成的直线为等值线.用等值线平行移动的方法来寻求最优解,是图解法的基本思想.在本文中,我们将要对这种方法进行改进,推广等值线的定义,以解决上文中提出的问题.

用图解法求解,见图1.从图中看到,在考虑具有P1,P2的目标实现后,x1,x2的取值范围为AB CD.下文中从整体上考虑P3的要求,即考虑min(2+).对于E点,我们有我们下面分四个区域来刻划的等值线P.区域甲,0

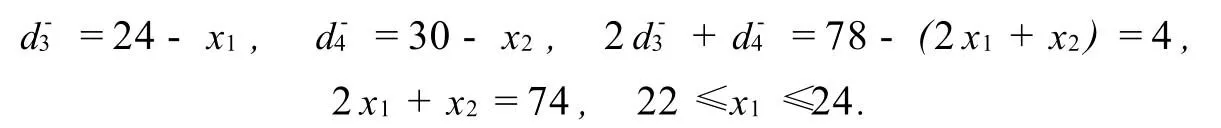
在这个区域内,P代表一个线段,两个端点分别是X(22,30)和E(24,26).区域乙,0≤x1≤24,x2≥30.此时,

在这个区域内,P代表一条与x2轴平行的射线,端点为X(22,30).区域丙,x1≥24,0≤x2≤30.此时,

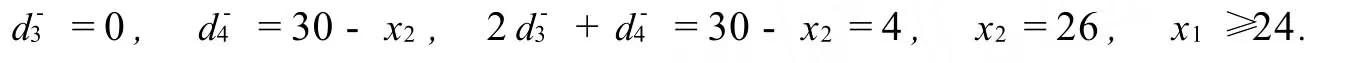
在这个区域内,P代表一条与x1轴平行的射线,端点为E(24,26).

区域丁,x1≥24,x2≥30.此时2+=4无解.在这个区域内,没有满足条件2+=4的点.

在上文中,我们选择刻划经过E点的等值线,令人信服地证明了E点为满意解.实际上,我们可以刻划经过任何一点的等值线,用等值线平行移动的方法得到经过任何其它点的等值线,从而寻求满意解.

4 改进等值线方法的进一步讨论

在下文中,我们看到,等值线也可以是闭合折线.考虑如下目标规划问题. minz=P1d+P2+P3(5+3)+P3(3+5d),

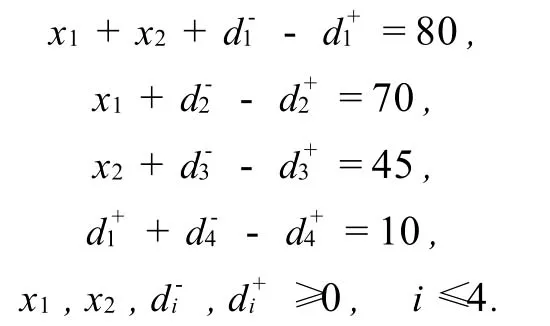
用图解法求解,见图2.从图中看到,在考虑具有P1,P2的目标实现后,x1,x2的取值范围为AB CD.下文中从整体上考虑P3的要求,即考虑min(5+3d+3d+5d).对于E点,我们有

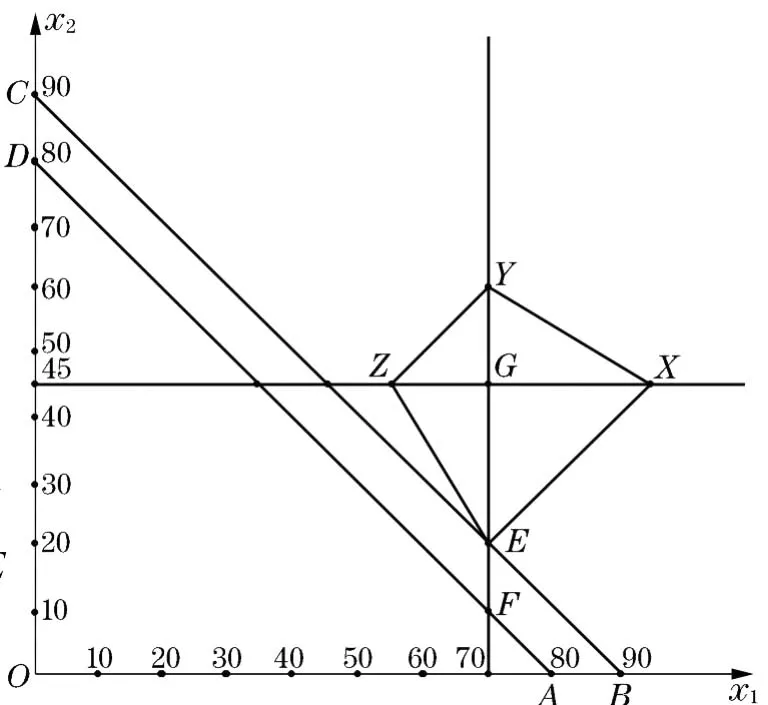
图2

区域甲,0≤x1≤70,0≤x2≤45.此时,

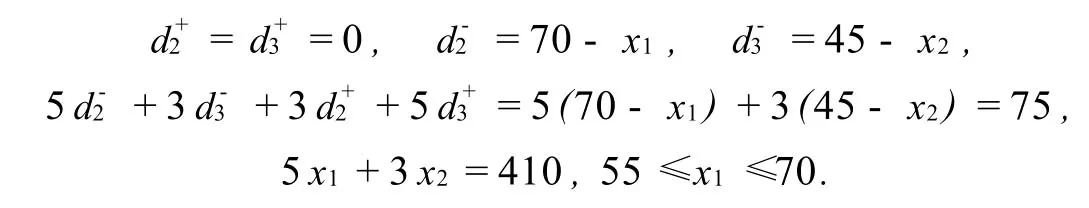
在这个区域内,Q代表一个线段,两个端点分别是Z(55,45)和E(70,20).

区域乙,0≤x1≤70,x2≥45.此时,

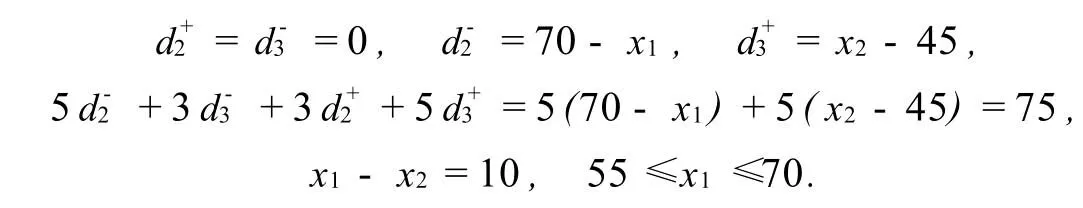
在这个区域内,Q代表一个线段,两个端点分别是Z(55,45)和Y(70,60).

区域丙,x1≥70,x2≥45.此时,

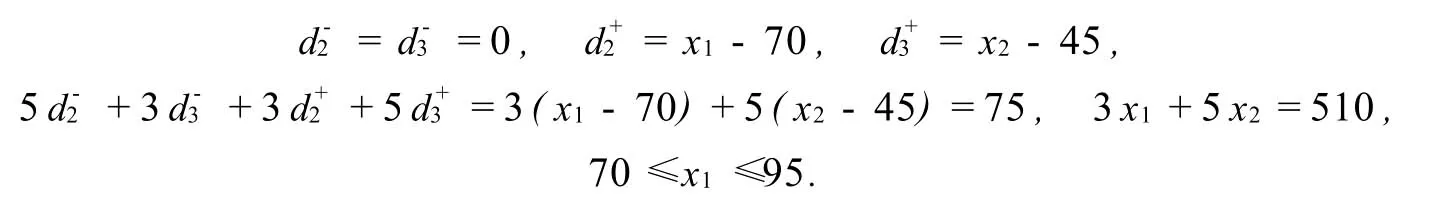
在这个区域内,Q代表一个线段,两个端点分别是X(95,45)和Y(70,60).

区域丁,x1≥70,0≤x2≤45.此时,

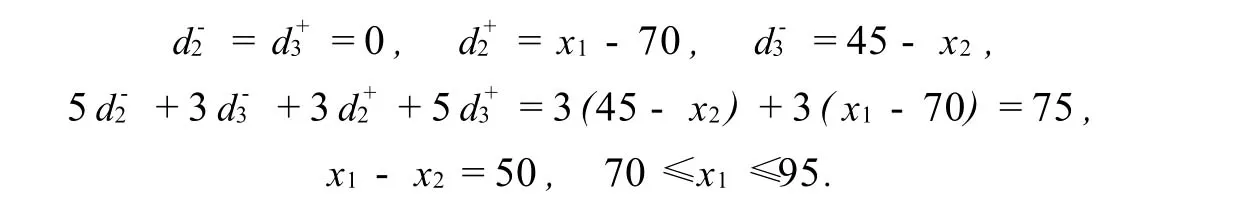
在这个区域内,Q代表一个线段,两个端点分别是X(95,45)和E(70,20).

[1] 甘应爱,田丰,等.运筹学[M].3版.北京：清华大学出版社,2005.

[2] 管梅谷,等.线性规划[M].济南：山东科技出版社,1983.

O211.6

C

1672-1454(2011)05-0146-03

2008-12-23; [修日期]2009-04-27