假设检验中p值的灵活运用
2011-11-22职桂珍徐雅静曲双红卢金梅汪远征
职桂珍, 徐雅静, 曲双红, 卢金梅, 汪远征
(郑州轻工业学院数学与信息科学系,河南郑州 450002)
假设检验中p值的灵活运用
职桂珍, 徐雅静, 曲双红, 卢金梅, 汪远征
(郑州轻工业学院数学与信息科学系,河南郑州 450002)
给出假设检验中p值的定义以及双边检验p值与单边检验p值的关系,介绍了利用p值将三种检验同时进行的方法及意义,最后给出应用实例.
假设检验;p值;拒绝域
假设检验是统计推断的重要内容,在很多经典的统计学教科书中,甚至是现在流行的概率统计教材中,大多采用计算检验统计量的观测值,并根据检验统计量的观测值是否落入拒绝域的方法做出能否拒绝原假设的推断.而现代统计软件中,假设检验多是采用计算p值的方法进行推断的.检验时需要由样本观测值计算出检验统计量的观测值和衡量观测结果极端性的p值,然后通过比较p值和显著水平的大小作判断:当p<,拒绝原假设H0;当p>,不能拒绝原假设H0.借助于统计软件,采用p值法进行假设检验方便、明了且便于了解检验结果显著性的程度.
然而,由于传统统计教学方法和现代软件使用的脱节,使很多人对p值的概念不清楚,不能灵活使用,或根本看不懂软件结果而无法解决应用问题.另一方面,有些统计软件可以方便地利用p值进行双边检验,却没有直接给出单边检验的过程和结果.如果对p值的计算没有深入探究,遇到单边检验问题,就会觉得软件不好使用.事实上,可以通过双边检验的p值计算出单边检验的p值,单双边检验可以同时进行,事半而功倍.本文深入介绍p值的计算公式并推出单双边检验中p值的关系,最后给出应用实例.
1 p值的定义与计算公式
p值就是当原假设成立时得到样本观测值和更极端结果的概率.若W为检验统计量,W0为W的观察值,通常p值由下面公式计算而得到.
1.双边检验的p值.
假设H0:θ=θ0;H1:θ≠θ0.
(i)检验统计量为对称分布的双边检验

(ii)检验统计量为非对称分布的双边检验
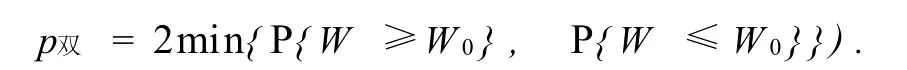
2.单边检验的p值
(i)拒绝域为右边区域的右边检验
假设H0:θ≤θ0;H1:θ>θ0.
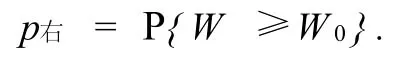
(ii)拒绝域为左边区域的左边检验
假设H0:θ≥θ0;H1:θ<θ0.
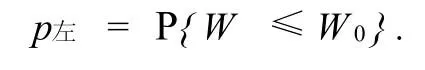
2 双边检验p值与单边检验p值的关系
根据上面p值的计算公式不难推出如下命题:
命题 设W为检验统计量,W0为W的观察值,W中为W的中位数,p双,p右和p左分别为双边检验H0:θ=θ0;H1:θ≠θ0,右边检验H0:θ≤θ0;H1:θ>θ0和左边检验H0:θ≥θ0;H1:θ<θ0的p值,则它们有下面关系:
1.检验统计量为对称连续分布时,
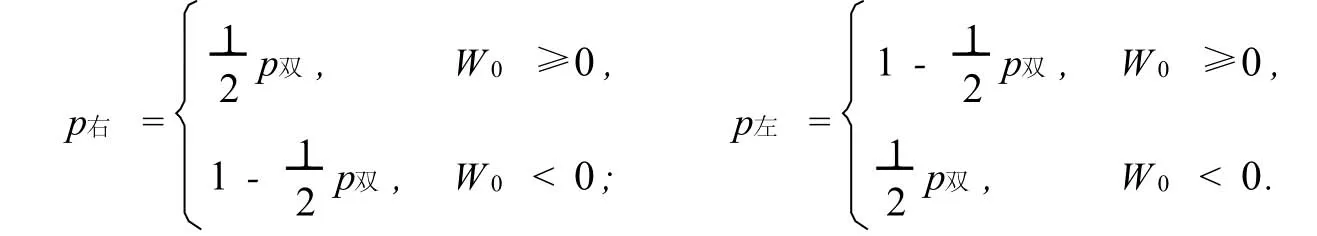
2.检验统计量为非对称分布时,
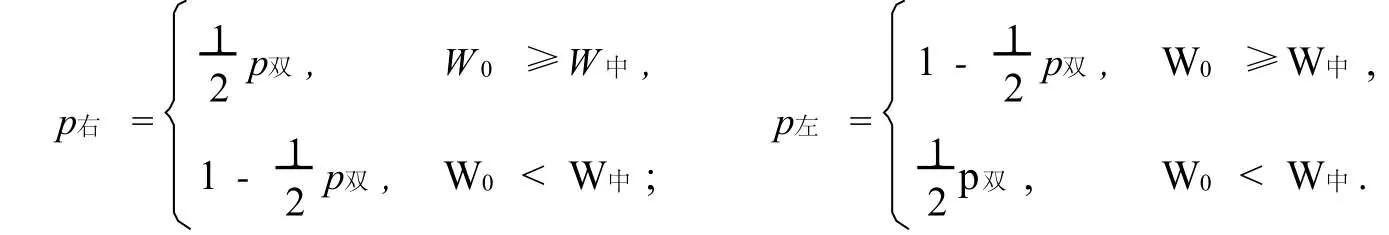
证1.检验统计量为对称连续分布时,由于
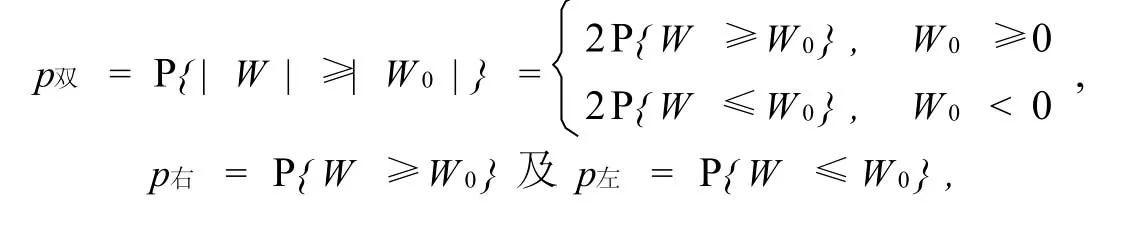
所以
(i)拒绝域为右边区域的右边检验,
若W0≥0,则p右=P{W≥W0}=p双/2;
若W0<0,则p右=P{W≥W0}=1-P{W<W0}=1-p双/2.
(ii)拒绝域为左边区域的左边检验,
若W0≥0,则p左=P{W≤W0}=1-P{W>W0}=1-p双/2;
若W0<0,则p左=P{W≤W0}=p双/2.
2.检验统计量为非对称分布时,由于
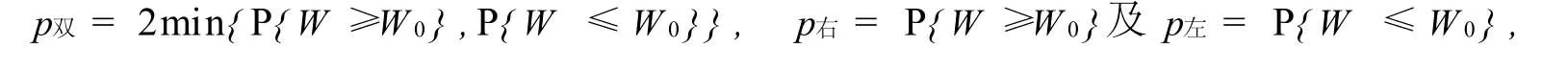
所以
(i)拒绝域为右边区域的右边检验,
若W0≥W中,则p右=P{W≥W0}=p双/2;
若W0<W中,则p右=P{W≥W0}=1-p双/2.
(ii)拒绝域为左边区域的左边检验
若W0≥W中,则p左=P{W≤W0}=1-p双/2;
若W0<W中,则p左=P{W≤W0}=p双/2.
知道双边检验的p值和单边检验的p值关系后,三种检验就可以一次完成.事实上,实际应用中只作一次双边检验或单边检验有时是不够的.比如在均值检验时,得到拒绝原假设μ=μ0的结论下,有时我们还需要进一步检验是否可以认为μ>μ0或μ<μ0才能得到较为准确的结论.即使是在得到不能拒绝原假设μ=μ0的结论下,如果双边检验的p值不够大(0.05<p<0.1),即拒绝备择假设μ≠μ0的证据较弱,往往也应该进一步作单边检验,以得到较为合理的μ≥μ0或μ≤μ0的结论.针对这两种情况,利用上述双边检验的p值和单边检验的p值关系,将三种检验同时进行就很有必要.
在考虑双边检验的p值和单边检验的p值关系时,当检验统计量为非对称分布时要用到检验统计量分布的中位数,可查阅有关分位数表,或用统计软件调用相应分位数函数进行计算.
3 应用实例
1.检验统计量为对称分布时.
例1 一家食品厂以生产袋装食品为主,每天的产量大约为8000袋,每袋重量规定为100克.为了分析每袋重量是否符合要求,质检部门经常进行抽检.现从某天生产的一批食品中随机抽取了25袋,测得每袋重量如表1所示.试从抽检的样本数据出发,检验袋装食品的平均重量与100克是否有显著差异.

表1 25袋食品的重量(单位:克)
分析与解答 设重量变量名为weight,本题是要求做原假设为μ=100的双边检验.但是根据检验p值与单边检验p值的关系,我们可以将三种检验同时进行.
(i)双边检验(H0:μ=μ0=100; H1:μ≠μ0,α=0.05).
在SAS中作t检验结果如图1.
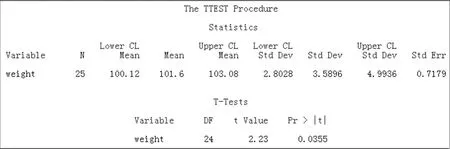
图1 t检验结果
从图中看到原假设μ=100的p双值为0.0355,在0.05的显著水平下,应该拒绝原假设.
(ii)右边检验(H0:μ≤100; H1:μ>100,α=0.05).
由于
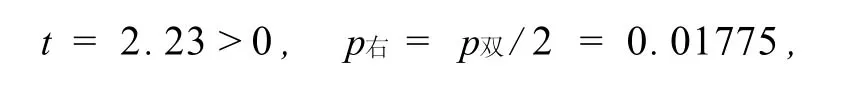
拒绝右边检验的原假设μ≤100.
(3)左边检验(H0:μ≥100; H1:μ<100,α=0.05).
由于
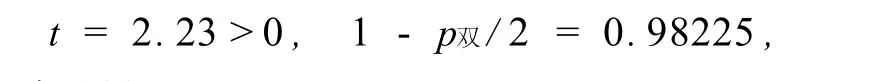
不能拒绝左边检验的原假设μ≥100.
综上,我们可以认为袋装食品的平均重量与100有显著差异,袋装食品的平均重量大于100克.
2.检验统计量为非对称分布时.
例2 某药材生产商要检查包装机械的状态.根据规定,包装机正常工作时,每袋重量为50克,方差为4.随机抽取当天生产的16袋样本称重后结果如表2所示,试考查药材包装机的状态是否正常.

表2 16袋药材重量(单位:克)
分析与解答 设重量变量名为weight,本题首先做原假设为σ2=4的双边检验,再根据双边检验p值与单边检验p值的关系,将三种检验同时进行,并综合分析三种情况作出判断.
(i)双边检验(H0:σ2=σ20=4; H1:σ2≠σ20,α=0.05).
在SAS中做方差的卡方检验结果如图2.
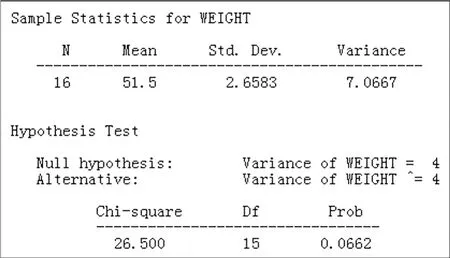
图2 χ2检验结果
从图中看到原假设σ2=4的p双值为0.0662,在0.05的显著水平下,不能拒绝原假设.
(ii)右边检验(H0:σ2≤4; H1:σ2>4,α=0.05).
由于自由度为15的χ2分布中位数为14.339,χ2=26.500>χ,p右=p双/2=0.0331<0.05,应拒绝右边检验的原假设σ2≤4.
(iii)左边检验(H0:σ2≥4; H1:σ2<4,α=0.05).
由于χ2=26.500>χ,p左=P{W≤W0}=1-p双/2=0.9669,不能拒绝左边检验的原假设σ2≥4.
综上,我们可以认为包装重量的方差不小于4,即认为现在包装机情况不够稳定,需维修.
例3 从机械厂的两台机器所加工的同一种零件中,分别抽出8个和9个样品,测量其尺寸如表3,试检验两台机器所加工零件的稳定性哪个较好?(α=0.05)

表3 两台机器所加工同一种零件的尺寸(单位:厘米)
分析与解答 设尺寸变量名为y,A机床加工该零件尺寸的方差为σ12,B机床加工该零件尺寸的方差为σ22.本题首先做原假设为σ12=σ22的双边检验,再根据检验p值与单边检验p值的关系,将三种检验同时进行,并进行综合分析作出判断.
(i)双边检验(H0:σ=σ; H1:σ≠σ,α=0.05).
在SAS中做两总体方差比的F检验结果如图3.
(ii)右边检验(H0:σ≤σ; H1:σ>σ,α=0.05).
由于自由度为(7,8)的F分布中位数为0.988,F=3.53>F中,p右=p双/2=0.0491<0.05,拒绝右边检验的原假设σ≤σ.
(iii)左边检验(H0:σ≥σ; H1:σ<σ,α=0.05).
由于F=3.53>F中,p左=P{W≤W0}=1-p双/2=0.9509,不能拒绝左边检验的原假设σ≥σ.
综上,我们可以认为A机床加工的零件尺寸的方差不比B机床加工的零件尺寸的方差小,即B机床加工的零件比A机床加工的零件尺寸更加稳定.
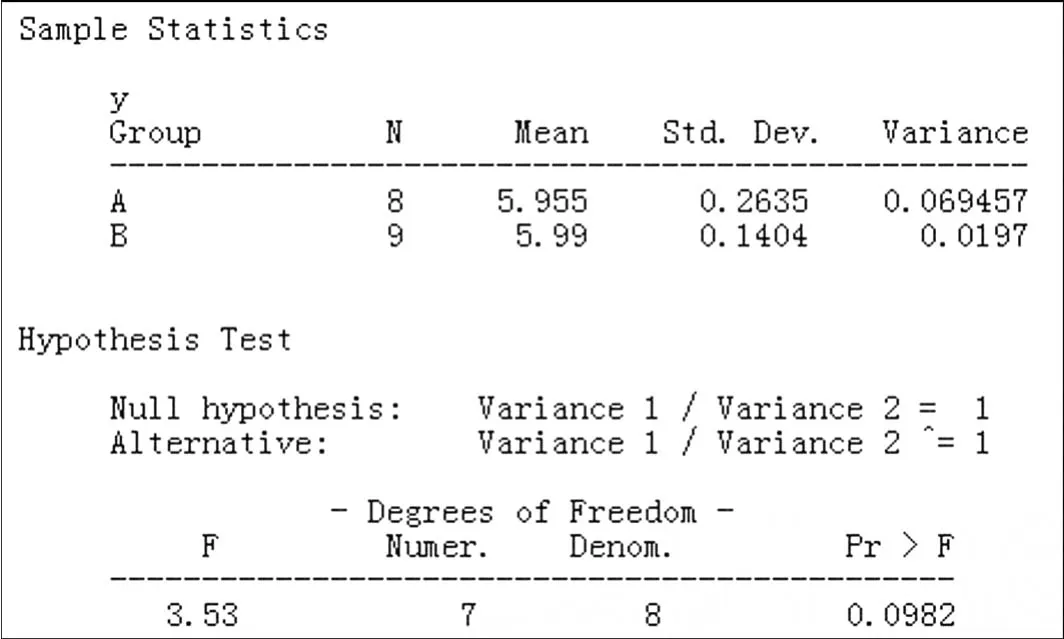
图3 F检验结果
4 结束语
在统计推断中掌握双边检验p值与单边检验p值的关系,不仅可以更加灵活地使用统计软件解决实际问题,而且可以三种检验同时进行使推断结果更加客观、符合实际.
[1] 峁诗松,程依明,濮晓龙,等.概率论与数理统计教程[M].北京:高等教育出版社,2004.
[2] 汪远征,徐雅静.SAS软件与统计应用教程[M].北京:机械工业出版社,2007.
[3] 薛薇,SPSS统计分析方法及应用[M].北京:电子工业出版社,2004.
[4] Gerald Keller,Brian Warrack.Statistics for managenment and economics[M].王琪延,郝志敏,廉晓红,等译.北京:中国人民大学出版社,2006.
[5] 谢明文.关于单侧检验拒绝的证明及假设检验的概率实质[J].北京:数学实践与认识,2004(10):99-103.
The Flexible Application of Valuepin Hypothesis Tests
Z HI Gui-zhen, XU Ya-jing, QU S huang-hong, L U J in-mei, WA N G Yuan-zheng
(Dept.ofMath.and Infor.Sci.,Zhengzhou Inst.of Light Ind.,Zhengzhou 450002,China)
Supplying with the definition of Valuepin the hypothesis tests and the relationship of Valuepin unilateral test and bilateral test,this paper introduced the method and significance of using Valuepto carry on the three kinds of tests synchronously,some applied exaples will be given in the end.
hypothesis tests;valuep;rejection region
O212.1
C
1672-1454(2011)05-0152-05
2009-01-11
郑州轻工业学院第八批教学改革与研究资助项目;郑州轻工业学院研究生教育教学第一批教改项目;郑州轻工业学院青年教师教学改革与研究项目
