运筹学课程教学中的探索与实践

王芳华, 冯春生

(湘潭大学数学与计算科学学院,湖南湘潭 411105)

运筹学课程教学中的探索与实践

王芳华, 冯春生

(湘潭大学数学与计算科学学院,湖南湘潭 411105)

结合教学实践经验,从提高学生的兴趣和积极性出发,在运筹学课程的教学过程中,提出了以学生为本,改进教学内容和教学方法,并把数学建模的思想融到运筹学课程的教学中去,从而提高学生的学习效果和教师的教学效果.

运筹学;数学建模;探索与实践

运筹学是一门新兴的应用学科,它充分利用现有的科学技术知识和数学方法,解决实践中提出的专门问题,为决策者选择最优决策提供定量依据.它广泛应用于工农业生产、经济管理、科学技术、国防事业等各个方面.正因为它应用的广泛性,才决定运筹学课程的重要性,因此在运筹学课程的教学过程中,必须不断地进行探索与实践,提高学生学习运筹学课程的兴趣和积极性,帮助他们更好地掌握这门学科,从而提高他们解决实际问题的能力.作者从事不同专业、不同层次的运筹学教学多年,并在运筹学课程的教学中一直不断地进行探索与实践,下面就介绍作者在教学中的一些粗浅体会.

1 以学生为本,改进教学内容和方法,提高学生学习的积极性

在线性规划中,单纯形法是解线性规划的一种最基本的方法,而这种方法的实现是通过单纯形表来完成的.这种单纯形表,它的功能与增广矩阵相似,从而在利用单纯形表进行计算时,迭代运算是通过行变换实现的,故计算时比较容易出错;并且每次迭代时,都需要重新利用基变量和非基变量的价值系数来计算检验数,由此可以看出,传统的单纯形表不够简便,计算比较麻烦,方法也容易忘记.学生在做运筹学课程[1]的作业题,尤其是线性规划部分的作业题时,由于决策变量的个数不仅仅是两个,所以线性规划模型的求解就不能统统利用图解法来求解,而是利用单纯形法来求解,这必然造成表格多,计算量大.学生做作业题时,往往方法、计算步骤和原理都掌握了,但仅仅由于表格中的某一个数字计算错误,造成计算结果错误,这不仅打击了学生学习运筹学课程的积极性,还使学生对自己计算能力的正确性产生了动摇.面对这种情况,经过多年的教学实践,对单纯形法进行了分析和研究,找到了一种比较好的解决办法,即通过对传统的单纯形表进行改进,提出了一种简易的单纯形表.

通过对单纯形表的观察和整个单纯形法迭代过程的研究后发现,在单纯形表中,基变量列在整个单纯形法迭代过程中都始终保持为一单位列向量,即其技术系统向量ei=(0,…,0,1,0,…,0)T,其中第i行为1,检验数为0,因此可以将单纯形表中的基变量列删除,便得到简易的单纯形表.设初始基可行解为X0=(b1,b2,…,bm,0,…,0)T,基变量向量XB=(x1,x2,…,xm)T,非基变量向量XN=(xm+1,…,xn)T,系数矩阵A=(B,N),其中A=(aij)n×m为基矩阵,B=(aij)m×m为基矩阵,N=(aij)n-m,m为非基矩阵,故简易的初始单纯形表如下:

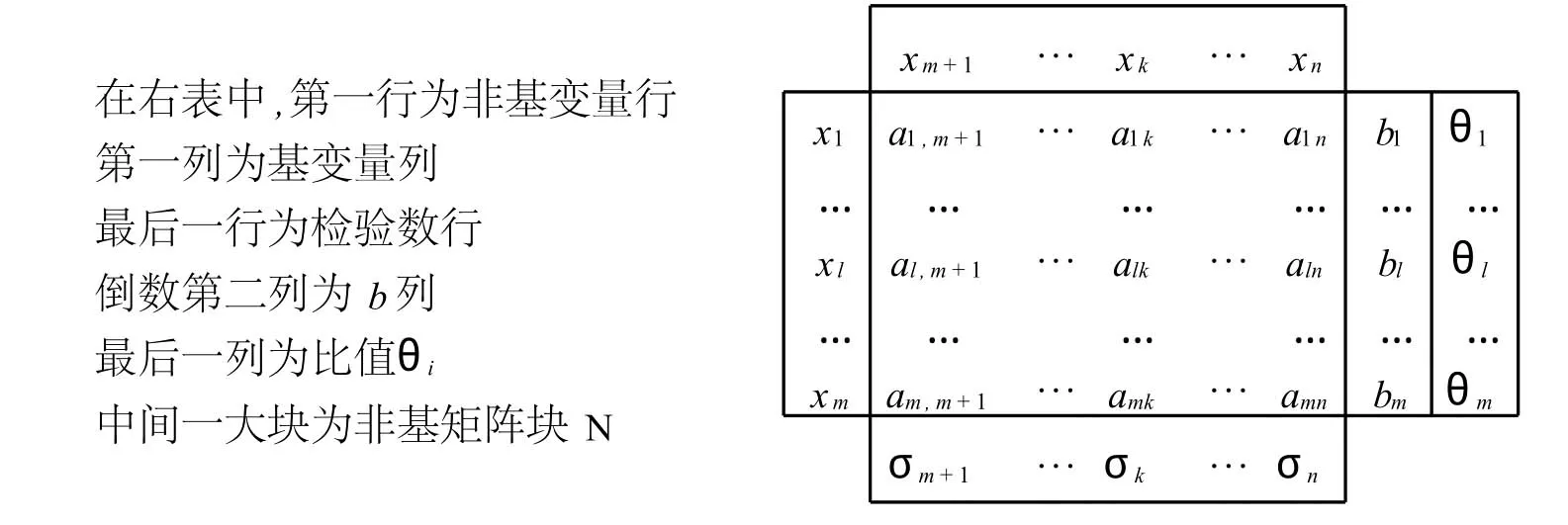
在单纯形法中,每迭代一次就得到一个新的简易单纯形表.当我们确定xk为换入变量,xl为换出变量时,就以alk为主元进行旋转运算,列出新的单纯形表.

在新的简易单纯形表中,非基变量形中的换入变量xk用换出变量xl替代,同样基变量列中的换出变量xl用换入变量xk替代,也可以形象地说在原表中,以主元alk为中心,换出变量xl顺时针方向旋转90°到达换入变量xk所在的位置并替代它,同样换入变量xk逆时针旋转90°到达换出变量xl所在的位置并替代它.并且在新表中,(i)主元:以1/alk表示(主元的倒数);(ii)主行:(除主元外)用主行除以主元(alk);(iii)主列:(除主元外)用主列除以负主元(-alk);(iv)其余元素(非主行主列上的元素)用矩形法则确定.

下面介绍矩形法则:设a,b,c,d为矩形的四个顶点,其中a为主元,b,c为主行、主列上的元素,d为非主行主列上的元素,则经过迭代后,d就变成d′=d-(即为对角线上的元素减去相邻元素的乘积除以主元).

在简易单纯形表中,容易知道:(i)非主行主列上的元素(包括检验数行上的元素σj和b列上的元素bi)都可以和主元构成一个矩形.(ii)主行或主列只要有一个元素为0,则在新表中相应的列或行保持不变.

在单纯形法中,如果采用这种简易的单纯形表,并在迭代过程中用矩形法则计算,可以大大地减少计算量(用传统的单纯形表解一个线性规划的平均运算工作量为O(m4+m2n)阶,而用简易的单纯形表解一个线性规划的平均运算工作量为O(3m2n+3n)阶)并使计算变得更加简单,计算方法也更加易记,而且在计算过程中也不容易出错;其次,这种简易的单纯形表的另外一个优点就是节省了存储量,即只要在开始利用变量的价值系数cj,j=1,2,…,n,来计算非基变量的检验数,然后在以后的计算中就可以直接利用矩形法则来计算非基变量的检验数了.

在运筹学课程的教学过程中,先讲授用传统的单纯形表的单纯形法,然后在此基础上,再顺理成章地讲解这种简易的单纯形表法,把这两种方法一比较,优劣非常明显.并且经过多年的教学实践表明:该法简单易行,学生不仅乐于接受而且也易于接受,这就帮助了学生解决了求解线性规划习题的困难,从而大大提高了学生学习运筹学课程的积极性,从而在教与学两方面都取得了比较满意的效果.

2 将数学建模的思想融入到运筹学课程的教学中,体现问题驱动的教学理念

运筹学是一门理论与实践相结合的应用学科,从它的各个分支来看,优化思想贯穿于这门学科的始终.而数学建模,自1992年中国工业与应用数学学会创办全国大学生数学建模竞赛以来,越来越受到高校教师和大学生的重视,它主要是培养学生运用数学知识去解决实际问题的能力,同时它也是优化思想的具体表现.因此,运筹学与数学建模的联系非常密切的.数学建模,是学生们运用数学知识创造性地建立模型去解决丰富多彩的实际问题,在这一过程中,学生们获益不少,故学生们对数学建模表现出了浓厚的兴趣和积极性.俗话说“兴趣是最好的老师”,兴趣更是学习最有效的动力.故如何提高学生学习运筹学的兴趣,真正学到运筹学的思想性的东西,培养学生创造性思维和具备运筹学的理论和方法去解决实际问题的能力,必须将数学建模的思想融入到运筹学课程的教学中去[2-3].

多年来,作者一直从事数学建模和运筹学这两门课程的教学.这两门课程既有相似之处,也有各自的特色,在运筹学课程的教学中,作者试图把数学建模的思想和精神融入到运筹学课程的教学中去,把运筹学里学生们认为是枯燥无味的概念、理论、方法讲得像数学建模一样有声有色、富有激情,从而提高学生们学习运筹学的兴趣和积极性.

一年一度的数学建模竞赛赛题,为讲授运筹学提供了丰富的素材,一方面是因为数学建模竞赛赛题来自于现实生活,紧跟时代潮流,涉及各个学科领域而且丰富多彩;另一方面是因为数学建模竞赛是一种选拔性竞赛,不是每个大学生都能参与的,对于大部分学生来说,虽然不能参与竞赛,但也希望能了解数学建模竞赛赛题.因此,选择一些历年数学建模竞赛赛题作为讲授运筹学的例题,可以大大提高学生学习的兴趣和求知欲.当然如何选取典型的数学建模竞赛赛题作为讲授运筹学的例题是一个比较复杂的问题,但作者认为选择的标准有三,一是所选的数学建模竞赛赛题应该要比运筹学教材中的应用性例题和习题更能反映解决问题的全过程;二是所选为数学建模竞赛赛题里所涉及的专业知识应该尽量是广大学生所能接受的,所需用到的运筹学知识,是符合教学内容要求的;三是所选数学建模竞赛赛题要有明确的目的,要与某个内容相联系,要为某种教学内容服务.

将数学建模的思想融入到运筹学课程的教学中去,并不是把运筹学课程变为数学建模课程、或者是数学试验课,而是有意识地结合运筹学的教学内容和学生的知识水平制造实际问题的情景,把学生引导到情景中来,让教师和学生一起发现运筹学的概念、理论和方法,再回到实践中去.

下面是将数学建模的思想和精神融入到运筹学课程的教学中去的一部分尝试.在讲解《运筹学》的第四章目标规划时,根据选择建模竞赛赛题的三个标准,挑选了2004年建模竞赛题目:公交车的调度模型.虽然乘坐共交车是生活的一部分,但我们很少用运筹学的理论和方法去分析它、优化它.故用这样一个贴近生活的实际问题作为讲解目标规划的例题,一下子就拉近了我们与运筹学中的抽象的概念、理论和方法的距离,很自然地把学生导入到实际问题的情景中来,然后水到渠成讲解目标规划的概念、理论和方法.

在公交车调度问题中我们边分析问题边引入概念,当分析到从乘客的利益出发,高峰时段乘客的候车时间不超过5分钟,即t1≤5,(t1为高峰时段的公交车的发车时间间隔,也可以理解为大多数乘客的平均候车时间),因上t1≤5是我们追求的第一个目标,其中5就是目标值,但是很明显不能把它作为模型的目标函数,故如何根据追求的第一个目标t1≤5,找到一个与之联系的目标函数呢?很容易根据坐公交车的经验,候车时间t1有可能大于5或者小于5,因此,把候车时间t1大于目标值5的那一部分,称为正偏差,记为,把候车时间t1小于目标值5的那一部分,称为负偏差,记为.从乘客的利益出发,希望候车时间t1小于目标值的那部分不限,但要尽可能缩小大于目标值5的那一部分正偏差,即为min,故第一个目标函数为min.同时要考虑目标函数min是不是会受到某些条件的约束呢?从乘客到站候车的这个过程来看,是一个随机的泊松过程,故希望候车时间t1的均值(数学期望值)应该等于目标值5,记为:t1+-=5,这就是目标函数所受到的约束条件,称为目标约束(即包含有正负偏差的等式约束条件),目标约束是一种软约束.同时可以分析平峰时段乘客的候车时间不超过10分钟,即t2≤10,(t2为平峰时段的公交车的发车时间间隔,也可以理解为大多数乘客的平均候车时间)的情况,即第二个目标函数为:min,目标约束为t2+-=10.

在公交车的调度问题中,不仅要考虑乘客的利益,而且也要考虑公交公司的利益.从公交公司的利益出发,公交车的平均载客率p≥50%,也就是说:要求超过目标值,即超过量不限,但要尽可能缩小没有达到载客率为50%的那一部分(负偏差),即第三个目标函数为:min,目标约束为: p+-=50%.

在公交车的调度问题中,由于公交车的容量有限,故存在一个最大载客率pmax=120%,所有的公交车的载客率都必须小于或等于120%,即为:p≤120%,这个约束条件是不能违背的,也就是说不允许发生p＞120%这种情况,这样的约束条件称为绝对约束,是一种硬约束.

通过以上分析,易知公交车的调度问题有三个目标需要考虑:t1≤5,t2≤10,p≥50%,故该公交车的调度问题模型为一个多目标规划(目标函数为两个或两个以上的规划),其中

在公交车的调度问题模型中,有三个目标需要达到,在考虑这些目标时,是有主次或轻重缓急的不同.当考虑到公交车的主要功能:社会公益性,并在满足这种前提的基础上,再考虑公交公司的利益,故可以把这多个目标分成不同的优先等级(优先因子),即把第一个目标(高峰时段达到的目标)赋予优先等级P1,这要求第一位达到的目标(主要目标);把第二个目标(平峰时段达到的目标)和第三个目标(公交公司达到的目标)赋予相同的优先等级P2,这是第二位要达到的目标(次要目标).规定P1≫P2,表示P1级目标比P2级目标有更大优先权,即首先保证P1级目标的实现,这时可不考虑次级目标(P2级目标);而P2级目标是在实现P1目标的基础上考虑的.对处在同一优先等级P2的两个目标(平峰时段达到的目标和公交公司达到的目标),又根据它们的重要程度,赋予不同的权重wj,其中1＞wj＞0, j=1,2,且w1+w2=1.故对高峰时段达到的目标有:P1d+1;对平峰时段达到的目标和公交公司达到的目标有:P2(w1d+2+w2d+3).经过上述分析,把关于公交车的调度问题的一个多目标规划模型转化成为只有一个目标函数的目标规划模型为

对此目标规划模型的结构它与线性规划模型的结构没有本质的区别,故可用单纯形法求解.

通过对公交车的调度问题的分析和建立其目标规划模型,使学生们很松地理解和掌握了目标规划的基本概念、理论和方法,从而提高了教和学的效果.

总之,在运筹学课程的教学过程中,通过不断地进行探索与实践,不断地改善教学内容和教学方法,并把数学建模的思想和精神不断地融入到运筹学课程的教学中去,使学生们对运筹学的学习不再枯燥乏味了,运筹学也变得生动有趣了;老师对运筹学的讲解也不再是枯燥的理论讲解了,而是在具体问题的解决中使知识的掌握更牢固了.

[1] 胡运权.运筹学教程[M].北京：清华大学出版社,1998.

[2] 张兵.案例教学在运筹学教学中的应用[J].徐州教育学院学报,2008,23(3)：153-154.

[3] 李苏北,等.运筹学课程建设与改革实践研究[J].大学数学,2005,21(5)：15-17.

Research and Pratics in Course of Teaching Operations Research

WA N G Fang-hua, FEN G Chun-sheng
(School of Mathematics and Computational Science,Xiangtan University,Xiangtan 411105,China)

Integrated with the experiences of pratical teaching activities,from the increased interest and enthusiasm of the students,teaching in the process of operational research,we present to the student-centered,improve teaching content and teaching methods,and to the idea of mathematical modeling is integrated into the teaching of opeartions research to improve student learning and teachers teaching effectiveness.

operations research;mathematical medeling;research and practice

G423

C

1672-1454(2011)05-0185-04

2011-05-24

湖南省教育厅资助科研项目(10C1289;10C1265)